Résumés
Résumé
Dans ce travail, nous suggérons l’utilisation de l’échantillonnage de Gibbs combiné à l’augmentation des données pour estimer des modèles à données longitudinales incomplètes, qui dans le cas extrême où l’échantillon est composé de coupes transversales indépendantes, correspond au cas de modèle de type pseudo-panel. Cette idée peut être appliquée dans plusieurs contextes : modèles statiques ou dynamiques de type linéaires, non linéaires, de choix discrets, avec régresseurs endogènes, etc. Pour présenter la méthode proposée, nous l’appliquons dans le cas d’un modèle linéaire à variable dépendante continue. Comme point de comparaison, nous utilisons les estimations par l’approche conventionnelle dite de pseudo-panel basée sur des moyennes calculées sur des cohortes. La technique proposée dans ce travail donne des résultats supérieurs, en terme d’efficacité, à la technique conventionnelle. Cette conclusion demeure valide quelle que soit la proportion des observations manquantes.
Abstract
In this paper, we suggest to use a Gibbs sampler with data augmentation to estimate models based on incomplete longitudinal data which, in the extreme case where the sample is composed of independent cross-sections, corresponds to a situation that normally calls for pseudo-panel modeling. The idea suggested here can be applied in several contexts: static and dynamic models linear or nonlinear type, discrete choice models, models with endogenous regressors, etc. To present the suggested method, we apply it to a linear model with continuous dependent variable. For comparison purpose, we also use the conventional pseudo-panel approach which is based on averages computed on cohorts. In terms of efficiency, the technique suggested in this work gives better results than the conventional pseudo-panel technique. This conclusion remains valid for any proportion of missing observations in the sample.
Corps de l’article
« Cette idée de travailler sur la théorie de la régression lorsqu’on dispose d’observations incomplètes, ça m’est venu effectivement d’un problème extrêmement pratique. (...) Il y avait des observations manquantes, et on avait l’impression que si on laissait tomber les questionnaires incomplets, on laissait tomber à peu près la moitié de l’échantillon, qui contenait pourtant beaucoup d’information. »
Marcel Dagenais
Introduction
Les données de panel, ou données longitudinales complètes, sont généralement cumulées à partir d’enquêtes répétées à travers le temps sur un même échantillon d’unités de base comme des individus, des ménages ou encore des entreprises. Ces données sont très utiles pour étudier la dynamique intertemporelle des comportements individuels. L’avantage principal des panels résulte du caractère désagrégé des observations et de la grande richesse d’information qui en découle.
Dans le cas où l’information est incomplète à travers le temps, et selon l’importance de l’information manquante, nous sommes en présence de panels dits incomplets ou non balancés. (Voir Baltagi, 1995a; Hirano, Imbens, Ridder et Rubin, 1998). Pour analyser l’évolution de la consommation des individus dans le temps, nous pouvons très bien nous retrouver avec une situation où l’information est complète pour la majeure partie des individus de l’échantillon, c.-à-d. l’information pour ces individus est disponible pour toutes les périodes de l’enquête, alors que pour un sous-groupe d’individus, les données sont absentes pour diverses raisons.
Nous pouvons imaginer le cas extrême, mais très répandu en pratique, où les informations sur chacune des unités de la dimension transversale ne sont présentes qu’à une seule période. Dans ce cas, nous sommes en présence de séries temporelles composées de coupes transversales indépendantes. Plusieurs auteurs ont traité ces cas limites, mais le premier chercheur qui a formalisé la méthodologie appropriée pour les traiter est Deaton (1985). Beaucoup d’autres études ont utilisé l’approche développée par Deaton, notamment Browning, Deaton et Irish (1985), Moffit (1993), Gardes, Langlois et Richeaudeau (1995), Alessie, Devereux et Weber (1997), Gardes et Loisy (1997), et Beaudry et Green (2000).
La solution proposée par Deaton est de créer des panels (au sens légitime du terme) à partir de moyennes prises sur des groupes d’unités classifiées selon des critères assurant une certaine homogénéité. Ces moyennes sur les informations des groupes d’unités, calculées à chaque période, constituent ce que nous appelons des pseudo-panels. Cette façon de faire permet de retrouver certains des avantages attribués aux panels, comme la possibilité de modéliser les effets dynamiques, tout en évitant certains des inconvénients qui leur sont propres. En particulier, les pseudo-panels permettent l’étude de comportements dynamiques sans avoir à être confronté aux problèmes d’attrition ou d’apprentissage. Nous qualifions cette technique de conventionnelle pour faire ressortir le fait que c’est l’approche la plus souvent utilisée pour traiter ces données et parce que les chercheurs font référence à cette technique lorsqu’ils parlent de pseudo-panels.
Les pseudo-panels sont générés en exploitant des séries de coupes tranversales provenant d’enquêtes indépendantes accumulées au fil des ans. De façon à obtenir un ensemble de données utiles, certaines règles doivent être respectées lors de la construction du pseudo-panel. Parmi ces règles, mentionnons la nécessité de conduire les enquêtes à partir d’une même population en utilisant la même méthodologie d’échantillonnage.
Une fois que les différentes enquêtes sont réunies, les unités, individus ou entreprises, qui ont des caractéristiques communes sont regroupées en cohortes de façon à ce que chaque unité n’appartienne qu’à une seule cohorte. De plus, cette appartenance à une cohorte doit être invariante dans le temps. La moyenne des unités à l’intérieur d’une cohorte est ensuite interprétée comme étant une observation du pseudo-panel. Un pseudo-panel peut donc être vu comme le résultat d’un ensemble de données longitudinales non balancées où chaque individu n’est présent qu’à une seule période dans les différentes enquêtes.
Nous proposons une méthodologie alternative à l’approche conventionnelle des pseudo-panels qui utilise, entre autre, la technique à augmentation de données (Tanner et Wong, 1987) afin de contourner le problème des données longitudinales incomplètes. La méthode résulte en des gains importants au plan de l’efficacité des estimateurs des paramètres des modèles. Nous considérons à la fois les panels partiellement incomplets et les combinaisons de coupes transversales indépendantes. Dans la première partie, nous présentons la problématique. Par la suite, nous expliquons les étapes spécifiques touchant l’estimation des paramètres. Nous terminons par une démonstration de la méthodologie proposée qui repose sur des données simulées.
1. Le problème
L’objectif de base vise à contourner les problèmes économétriques qui découlent généralement du phénomène de données manquantes. Bien que l’approche développée s’applique tout aussi bien dans des situations de modèles linéaires simples que dans le cas de modèles de choix discrets dynamiques pouvant même comporter des régresseurs endogènes, pour des fins pédagogiques, nous focalisons dans le présent texte sur le modèle de régression linéaire avec variable dépendante continue. Dans un premier temps, nous présentons la notation du modèle linéaire utlisé. Le modèle comprend des effets individuels aléatoires. Ces effets sont souvent nécessaires dans les études empiriques car ils permettent de tenir compte de l’hétérogénéité individuelle non observable. Nous expliquons dans un premier temps la technique conventionnelle et les estimateurs qui s’y rattachent, ainsi que la construction des cohortes utilisées dans notre application empirique. Finalement, nous présentons la technique que nous proposons, laquelle exploite l’échantillonage de Gibbs couplé avec le principe d’augmentation de données.
1.1 Le modèle économétrique
Le modèle utilisé dans ce travail pour illustrer la technique proposée pour l’analyse des pseudo-panels est le suivant :
Dans cette version du modèle, sans perte de généralité, xnt représente une seule variable explicative. La structure des erreurs est la suivante :
où θn est un effet aléatoire invariant dans le temps et νnt représente le terme d’erreur résiduel. Les termes d’erreurs θn et νnt sont considérés comme étant indépendants entre eux. De plus, xnt est postulé comme étant indépendant de θn et de νnt pour tout n et tout t. Les modèles avec effets aléatoires sont appropriés lorsque qu’il est raisonnable de considérer que les individus de l’échantillon sont tirés aléatoirement d’une large population.
Sous les hypothèses faites, la matrice de variances-covariances de l’erreur composée unt est définie par :
Pour assurer un bon contrôle dans le cadre de notre application empirique, nous exploitons des données simulées générées selon un modèle bien précis. Pour simuler les variables explicatives, nous utilisons le modèle de régression auxiliaire suivant :
avec εnt ~ N(0, τ2) .
1.2 Approche à pseudo-panels
La solution au problème de la non-disponibilité des données de panel, proposée par Deaton (1985), est de créer des panels (au sens légitime du terme) à partir de moyennes prises sur des groupes d’unités classifiées selon des critères assurant une certaine homogénéité. Ces moyennes sur les informations des groupes d’unités, calculées à chaque période, constituent les pseudo-panels. Cette façon de procéder permet de retrouver certains des avantages attribués aux panels tout en évitant certains des inconvénients qui leur sont propres.
Plusieurs travaux (Heckman et Robbs, 1985; Deaton, 1985; Moffit, 1993) ont suggéré qu’il n’était pas indispensable d’avoir de vrais panels pour arriver à identifier et à estimer les effets de dynamique des modèles traditionnels.
L’idée proposée par Deaton consiste à regrouper ensemble les individus ayant des caractéristiques communes de façon à former des cohortes. Une fois les observations groupées, ce sont les moyennes des différentes variables explicatives qui font office d’unités et qui constituent le pseudo-panel. De façon à bien comprendre la procédure de formation des pseudo-panels, exploitons le modèle linéaire présenté à l’équation (1). Avec un ensemble de coupes transversales indépendantes, il faut réaliser que les N individus présents à chaque période diffèrent. Maintenant, définissons un ensemble de C cohortes dont chacune d’elle possède des critères d’appartenance invariables dans le temps. L’année de naissance et le sexe de l’individu constituent de bon critères pour former les cellules. Chaque individu n ne peut appartenir qu’à une seule cohorte c. Lorsque nous agrégeons les individus en cohortes et que nous calculons les moyennes intracohortes, cela donne :
où ȳct représente la moyenne de tous les ynt qui font partie de la cohorte c à la période t et il en va de même pour les autres variables du modèle. Il est important de constater que l’effet spécifique aux cohortes devient maintenant variable dans le temps. Ceci est dû au fait que nous n’observons pas les mêmes individus d’une période à l’autre et, par conséquent, la moyenne devient dépendante de l’indice temporel. Vient s’ajouter à cela le fait que, la plupart du temps, ![]() est corrélé avec xnt. Le choix du type d’effets considérés, à savoir fixes ou aléatoires, amène aussi son lot de problèmes. Alors que les effets fixes nous conduisent au problème d’identification, les effets aléatoires peuvent mener à des estimations non convergentes, si la corrélation potentielle entre
est corrélé avec xnt. Le choix du type d’effets considérés, à savoir fixes ou aléatoires, amène aussi son lot de problèmes. Alors que les effets fixes nous conduisent au problème d’identification, les effets aléatoires peuvent mener à des estimations non convergentes, si la corrélation potentielle entre ![]() et xnt n’est pas prise en compte. Pour ces raisons, ce dernier modèle n’est pas celui qui sera utilisé afin d’obtenir des estimateurs convergents, à moins que la taille des cohortes permette de dire que
et xnt n’est pas prise en compte. Pour ces raisons, ce dernier modèle n’est pas celui qui sera utilisé afin d’obtenir des estimateurs convergents, à moins que la taille des cohortes permette de dire que ![]() est une bonne approximation de
est une bonne approximation de ![]() Une façon de s’assurer que
Une façon de s’assurer que ![]() est d’avoir un grand nombre d’observations dans chacune des cohortes (Verbeek et Nijman, 1992).
est d’avoir un grand nombre d’observations dans chacune des cohortes (Verbeek et Nijman, 1992).
Dans le cas où le nombre d’observations dans chaque cohorte n’est pas très grand, nous pouvons utiliser la version du modèle avec la vraie population des cohortes dans le but d’avoir des estimateurs convergents, soit :
avec y*ct et x*ct représentant les moyennes non observables de la population des cohortes et θc l’effet spécifique aux cohortes. Comme la vraie population d’une cohorte est la même dans le temps, θc est invariant dans le temps. Deaton propose l’utilisation d’un estimateur corrigé pour tenir compte d’erreurs sur les variables. Ces erreurs proviennent du fait que les moyennes intracohortes du modèle (5) sont en réalité des mesures imparfaites de y*ct et x*ct. Ici, toutes les variables sont estimées avec erreurs de mesures à l’exception de θc.
Cependant, dans la pratique, le problème d’erreurs de mesure sur les variables est ignoré dès que le nombre d’observations à l’intérieur de chacune des cohortes est élevé (voir Browning et al., 1985; Blundell et al., 1990; Moffit, 1993). Dans ce cas, l’estimateur le plus souvent utilisé est le suivant :
où ![]() Cet estimateur est connu sous le nom de « within » parce qu’il utilise l’information qui provient de la variabilité entre les observations de la dimension individuelle contenue dans une cohorte en particulier. Dans le cas où les effets sont fixes, l’estimateur de θc est
Cet estimateur est connu sous le nom de « within » parce qu’il utilise l’information qui provient de la variabilité entre les observations de la dimension individuelle contenue dans une cohorte en particulier. Dans le cas où les effets sont fixes, l’estimateur de θc est ![]() Nous pouvons aussi définir un estimateur qui privilégiera l’information qui provient de la variabilité entre les cohortes. C’est l’estimateur « between » qui s’écrit :
Nous pouvons aussi définir un estimateur qui privilégiera l’information qui provient de la variabilité entre les cohortes. C’est l’estimateur « between » qui s’écrit :
Afin que ces estimateurs soient convergents, Verbeek et Nijman (1992) montrent que la taille des cohortes doit tendre vers l’infini et que la convergence de l’estimateur « within » sera assurée si les conditions suivantes sont respectées :
et 
Par ailleurs, ils montrent pour certains modèles assez simples que le problème d’erreurs de mesure devient négligeable lorsque la taille des cellules est assez grande (quelques centaines d’individus par cellule).
1.3 Les cohortes dans la présente application
La construction même des cohortes doit respecter certaines règles bien précises. Par exemple, les cellules doivent être définies sur la base d’une variable distribuée de façon continue que nous appelons s. Cette variable doit être distribuée de façon indépendante entre les individus et doit posséder une variance normalisée à l’unité. De plus, les cohortes sont construites de telle sorte que la probabilité non conditionnelle d’appartenir à une cohorte donnée est la même pour tous les individus.
Dans la pratique, la variable s est généralement basée sur plus d’une variable sous-jacente. Cependant, il faut bien comprendre que les critères d’association des cellules excluent certaines variables de choix. Par exemple, une variable qui ne serait pas constante pour chaque individu à chaque période ne pourrait être utilisée car cela impliquerait que certains individus perdraient leur droit d’appartenance à une cellule bien définie. D’autre part, la variable de choix se doit d’être observable pour tous les individus de l’échantillon. Ceci implique que des variables tels le revenu du chef de famille ou la taille de la famille ne sont pas de bons candidats à la construction de la variable s permettant de définir les cohortes. Pour plus de détails, consulter Verbeek et Nijman (1992).
Cette façon de procéder permet de conserver exactement le même nombre de séries temporelles mais a le grand désavantage de réduire considérablement le nombre d’observations de chaque tranche transversale présente dans le pseudo-panel. Par ailleurs, la définition des cohortes joue aussi un rôle important dans l’efficacité des estimateurs : la détermination même des cohortes, c.-à-d. la taille et le nombre, a un impact important sur la taille du biais et de la variance des estimateurs dans un contexte d’échantillons finis (Verbeek et Nijman, 1993).
Les observations sont regroupées en cellules à l’aide de la variable s qui est invariante dans le temps et qui est observable pour toutes les personnes à toutes les périodes. Pour fins d’illustration, nous n’avons utilisé qu’une seule variable pour construire les cellules. Afin de pouvoir appliquer la méthodologie des cohortes telle que définie précédemment, l’ensemble complet est divisé en 6 cohortes sur la base de la distribution d’une variable znt appartenant à la régression auxiliaire (4).
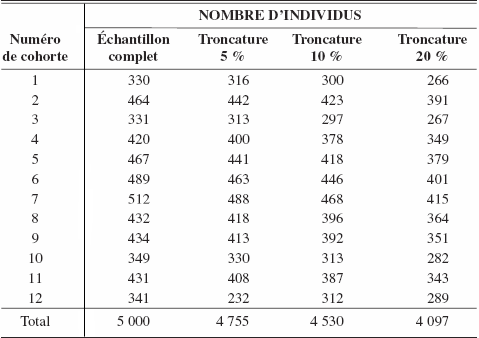
Dans cet ensemble d’expériences, nous nous plaçons dans un contexte à deux périodes où, pour chaque expérience, le nombre d’observations manquantes est approximativement de 5 %, 10 % et de 20 % . Expliquons le principe retenu pour l’échantillon à 5 %. Pour le créer, nous avons enlevé de façon aléatoire 5 % des 5 000 observations de chacune des périodes, en nous assurant par contre qu’une observation ne peut être manquante dans les deux périodes. Le même principe est appliqué pour générer les échantillons à 10 % et à 20 % d’observations manquantes. Les décomptes du nombre résultant d’observations par cohortes sont donnés aux tableaux 1 et 2. Le tableau 1 concerne la première période alors que le tableau 2 concerne la deuxième période.
Tableau 1
Nombre de cohortes = 6, t = 1
Tableau 2
Nombre de cohortes = 6, t = 2
Par la suite, le même ensemble de données est divisé en 8 et 12 cohortes et la même méthodologie est appliquée pour l’estimation des paramètres. Le nombre d’observations pour ces deux autres structures d’ensembles de données est présenté à l’annexe A.
1.4 Échantillonnage de Gibbs et augmentation de données
L’approche bayésienne repose sur la distribution a posteriori :
où θ représente le vecteur des paramètres. L(θ | Y) qui constitue une réécriture de p(Y | θ) représente la fonction de vraisemblance et p(θ) la densité qui correspond à la distribution a priori de θ. L’échantillon observable est constitué des variables ynt et xnt auquel nous ajoutons les observations qui étaient manquantes et qui sont indexées d’un m. Par conséquent, l’échantillon complet s’écrit Y = {Yob, Y*} où Y* = {ymt, xmt} et Yob = {ynt, xnt}.
La densité conditionnelle qui nous intéresse s’obtient en intégrant par rapport aux données manquantes :
Il est toutefois fréquent que la forme de cette densité ne soit pas connue. Par ailleurs, l’évaluation de la fonction de vraisemblance, à cause de la présence des observations manquantes, peut nécessiter un temps de calcul considérable et ce, malgré la performance croissante des ordinateurs.
Pour contourner ces différents problèmes, nous utilisons la technique dite d’augmentation de données. Cette technique permet de traiter tous les éléments non observables du modèle comme s’ils étaient des paramètres à estimer. L’idée est la suivante : si nous connaissons Y*, nous pouvons calibrer une valeur raisonnable pour le vecteur des paramètres θ; si nous connaissons θ, nous pouvons estimer les données manquantes, c.-à-d. Y*. Pour arriver à mettre ce principe en application, il est essentiel de pouvoir tirer des données des distributions suivantes :
et ![]()
Dans la plupart des cas, effectuer des tirages à partir des distributions conditionnelles ne pose pas de problème grâce à la technique d’échantillonnage de Gibbs. Pour plus de détails sur l’échantillonnage de Gibbs, consulter Casella et George (1992), Gordon et Bélanger (1996) ou Paquet (2002).
2. Estimation économétrique
L’approche proposée est divisée en deux étapes. Dans la première, nous utilisons la technique d’augmentation de données afin de simuler les données manquantes. Dans la seconde, nous simulons le vecteur des paramètres étant donné les données augmentées.
2.1 L’étape de l’augmentation des données
Étant donné les hypothèses faites sur le modèle, cette étape s’effectue comme suit :
Étape 1 : simulation de ymt
Étant donné xmt, où m dénote une observation individuelle manquante, et les paramètres du modèle, nous remarquons à partir de l’équation (1) qu’il est possible de simuler ymt comme suit :
et ![]()
Les valeurs pour ymt sont simulées à partir d’une distribution normale
où Y[m] est un vecteur de tous les ymt et Ω[m] est la sous-matrice de Ω qui correspond uniquement aux observations manquantes. La matrice Ω est définie à l’équation (24) de l’annexe B.
Étape 2 : simulation de xmt
Maintenant, nous devons simuler les données manquantes de la variable xmt. Pour ce faire, nous utilisons la régression auxiliaire présentée à l’équation (4). La distribution conditionnelle d’intérêt est obtenue à partir des hypothèses faites sur le modèle :
En combinant (15) et (16) nous pouvons isoler la contribution de X[m], ce qui donne
et ![]()
L’annexe B présente tous les calculs associés à cette distribution conditionnelle, dont le résultat dans le cas d’une seule variable xmt s’écrit :
Étant donné les autres éléments du modèle, ceci nous fournit la possibilité de simuler les valeurs pour tous les xmt.
2.2 L’étape de la simulation du vecteur des paramètres
Une fois que les tirages pour les données manquantes sont obtenus, l’estimation du vecteur des paramètres découle de l’application de résultats bien connus en économétrie bayésienne touchant le modèle de régression linéaire.
Étape 3 : simulation de β
Si les croyances a priori sur β sont décrites comme suit ![]() et si σ2u est connu, alors le modèle devient une simple régression avec variance connue. Dans ce cas, nous pouvons montrer que
et si σ2u est connu, alors le modèle devient une simple régression avec variance connue. Dans ce cas, nous pouvons montrer que
où ![]()
Par conséquent, simuler β implique le tirage d’une valeur à partir d’une distribution normale multivariée.
Étape 4 : simulation de σ2u
Étant donné β et les données, il est possible de récupérer directement le vecteur d’erreur u = Y – X β. Si les croyances a priori sur σ2u sont décrites par p(σ-2u) = G(ā, b̄), alors les valeurs de σ2u sont simulées à partir de la distribution a posteriori
qui représente une distribution Gamma avec moyenne ãb̃ et variance ãb̃2 connues.
Étape 5 : simulation de γ
Étant donné Znt et τ2, la régression auxiliaire présentée à l’équation (4) est encore une fois un modèle de régression avec variance connue. Lorsque les croyances a priori pour γ sont représentées par ![]() alors
alors
où ![]()
Étape 6 : simulation de τ2
Tout comme dans le cas de la simulation de σ2n, étant donné X, Z et γ, nous pouvons récupérer ∈ = X – Z γ. Si les croyances a priori sur τ2 sont représentées par une loi gamma inverse p(τ-2) = G(c̄, d̄), alors τ-2 est simulé à partir de la distribution gamma suivante :
Encore une fois, les deux premiers moments de la distribution sont connus, soit la moyenne c̃d̃ et la variance c̃d̃2.
3. Les résultats d’estimation
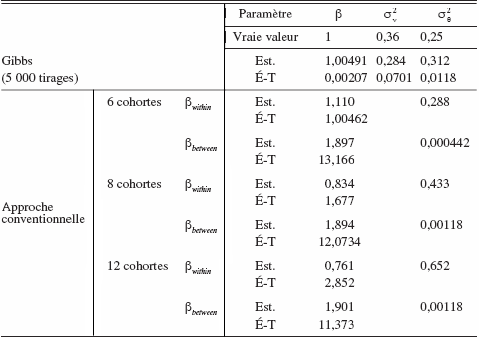
Pour comparer les deux techniques d’estimation, le point de référence est l’estimation par échantillonnage de Gibbs sans augmentation de données obtenue à partir de l’ensemble complet de données de panel. Dans ce cas, la banque de données simulées est composée de 5 000 observations pour chacune des deux périodes. À la lumière du tableau 3, il est possible de retirer certaines constatations quant aux performances respectives des deux techniques d’estimation, soit la méthodologie à cohortes représentatives (la méthode à pseudo-panels) et l’échantillonnage de Gibbs avec augmentation de données.
Les résultats obtenus sont très bons et la petitesse des écart-types suggère que les paramètres sont estimés avec un haut degré de précision. Pour la méthodologie des cohortes, les résultats sont affectés par le nombre de cellules utilisées dans la création des différents échantillons. Les résultats basés sur 6, 8 ou 12 cellules sont présentés au bas du tableau 3. Au fur et à mesure que le nombre de cellules augmente, les résultats des estimations between s’améliorent mais la précision des estimations demeure bien en deçà de celle obtenue à l’aide de l’échantillonnage de Gibbs. De la même façon, les résultats des estimations within deviennent moins précis lorsque le nombre de cellules augmente car cela implique que moins d’observations sont utilisées dans chacune d’elles. Étant donné que l’estimateur within utilise la variation à l’intérieur de la cellule, ce résultat n’est pas du tout surprenant.
Tableau 3
Résultats d’estimation en panel (N = 5 000, t = 2)
Pour l’échantillonnage de Gibbs avec augmentation de données, c.-à-d. dans le contexte où nous procédons à une troncature des échantillons, les résultats demeurent très intéressants. Cependant, lorsque le nombre de données manquantes augmente, c.-à-d. lorsque nous passons d’une troncature de 5 %, à 10 % puis à 20 %, les résultats perdent quelque peu de leur précision (voir les tableaux 4, 5 et 6). Par contre, pour la méthodologie des cohortes, le nombre de cellules formées à l’aide de l’échantillon de départ ne semble plus être le facteur critique. C’est plutôt le niveau de troncature de l’échantillon qui devient le facteur clé.
Tableau 4
Résultats d’estimation en pseudo-panel tronqué à 5 %
Tableau 5
Résultats d’estimation en pseudo-panel tronqué à 10 %
Tableau 6
Résultats d’estimation en pseudo-panel tronqué à 20 %
Conclusion
L’objectif de ce travail a été de proposer une approche alternative à la technique conventionnelle des pseudo-panels en utilisant les techniques à augmentation de données (Tanner et Wong, 1987). L’approche suggérée utilise au maximum toute l’information disponible au lieu de réduire l’information des unités à un niveau de définition qui correspond à des moyennes de groupes. Elle est d’ailleurs si flexible qu’elle peut être utilisée pour traiter tant le cas extrême soulevé par Deaton, soit la combinaison de coupes transversales indépendantes, que les situations de panels incomplets proprement dits.
Pour fins de démonstration, la méthodologie suggérée est appliquée dans le contexte d’un modèle linéaire à erreurs composées et elle est comparée à la technique conventionnelle des pseudo-panels. L’estimation est produite à partir de bases de données synthétiques. Les résultats indiquent que la méthode proposée est très prometteuse car les résultats sont de loin supérieurs à ceux obtenus par la méthode conventionnelle des pseudo-panels. Par ailleurs, l’approche est très flexible et est directement applicable à tous les types de modèles linéaires, avec erreurs aléatoires ou à effets fixes. Cette méthode devient d’autant plus intéressante dans un contexte de modèles à choix discrets (Paquet, 2002).
Parties annexes
Annexes
Annexe A
Nombre de données dans chaque cellule
Voici le nombre d’observations par cellule pour chaque ensemble de données utilisé pour l’estimation du modèle linéaire.
Tableau 7
Nombre de cohortes = 8, t = 1
Tableau 8
Nombre de cohortes = 8, t = 2
Tableau 9
Nombre de cohortes = 12, t = 1
Tableau 10
Nombre de cohortes = 12, t = 2
Annexe B
Distribution conditionnelle pour le modèle linéaire univarié
Soit le modèle linéaire suivant que l’on exprime sous forme matricielle comme suit :
et ![]()
où ιT est un vecteur de uns de dimension T. La matrice des variances-covariances s’écrit alors :
La régression auxiliaire pour sa part s’écrit :
et ![]()
Selon les hypothèses faites sur le modèle, nous pouvons déduire les distributions conditionnelles suivantes :
et
Lors de l’application, nous retenons une seule variable explicative. Par conséquent, le modèle est défini comme suit :
et ![]()
où n = 1, 2, ..., N et t = 1, 2, ..., T, avec la structure suivante pour les termes aléatoires :
et ![]()
En ce qui a trait à la régression auxiliaire permettant de simuler les variables manquantes, nous avons, sous l’hypothèse d’une seule variable explicative pour cette régression, la relation suivante :
et ![]()
Nous pouvons maintenant réécrire les équations de probabilité conditionnelle comme suit :
En combinant les équations (30) et (31) nous obtenons la distribution conditionnelle suivante :
qui est le noyau d’une distribution normale ![]() avec
avec
et ![]()
Remerciements
Cette recherche a bénéficié du soutien financier du FQRSC (FCAR) et du CRSH. Nous tenons à remercier Stephen Gordon pour ses multiples conseils judicieux.
Bibliographie
- Alessie, R., M.P. Devereux et G. Weber (1997), « Intertemporal Consumption, Durables and Liquidity Constraints: A Cohort Analysis », European Economic Review, 41 : 37-59.
- Baltagi, B. (1995a), Econometric Analysis of Panel Data, John Wiley Sons, Chischester, England.
- Baltagi, B. (1995b), « Panel Data », Journal of Econometrics, 68 : 1-243.
- Beaudry, P. et D. Green (2000), « Cohort Patterns in Canadian Earnings: Assessing the Role of Skill Premia in Inequality Trends », Canadian Journal of Economics, 33(4).
- Blundell, R. et C. Meghir (1990), « Panel Data and Lify-Cycle Models », in J. Hartog, G. Ridder et J. Theeuwes, (éds), Panel Data and Labor Market Studies, North Holland, Amsterdam, p. 231-252.
- Browning, M. A. Deaton et M. Irish (1985), « A Profitable Approach to Labor Supply and Commodity Demands Over the Life Cycle », Econometrica, 53 : 503-543.
- Casella, G et E. George (1992), « Explaining the Gibbs Sampler », The American Statistician, 46 : 109-126.
- Deaton, A. (1985), « Panel Data from Time Series of Cross Sections », Journal of Econometrics, 30 : 109-126.
- Gardes, F., S. Langlois et D. Richaudeau (1996), « Cross-Section Versus Time Series Income Elasticities of Canadian Consumption », Economic Letters.
- Gardes, F. et C. Loisy (1997), « La pauvreté selon les ménages : une évaluation subjective et indexée sur leur revenu », Économie et Statistique, 308-309-310 : 95-113.
- Gordon, S. et G. Bélanger (1996), « Échantillonnage de Gibbs et autres applications des chaînes markoviennes », L’Actualité économique, 72(1) : 27-49.
- Heckman, J.J. et R. Robbs (1985), « Alternative Models for Evaluating the Impact of Interventions: An Overview », Journal of Econometrics, 30 : 239-267.
- Hirano, K., G.W. Imbens, G. Ridder et D.B. Rubin (1998), « Combining Panel Data Sets with Attrition and Refreshment Samples », Technical Working Paper 230, National Bureau of Economic Research, Cambridge, MA.
- Moffit, R. (1993), « Identification and Estimation of Dynamic Models with a Time Series of Repeated Cross-Sections », Journal of Econometrics, 59 : 99-123.
- Paquet, M.-F.(2002), « Une approche à simulation pour le traitement des données longitudinales incomplètes », Thèse de doctorat, Université Laval.
- Tanner, M.A. et W.H. Wong (1987), « The Calculation of Posterior Distributions by Data Augmentation », Journal of the American Statistical Association, 82(398) : 528-540.
- Verbeek, M. et Th.E. Nijman (1992), « Can Cohort Data Be Treated As Genuine Panel Data? », Empirical Economics, 17 : 9-23.
- Verbeek, M. et Th.E. Nijman (1993), « Minimum MSE Estimation of a Regression Model with Fixed Effects and a Series of Cross-Sections », Journal of Econometrics, 59 : 125-136.
Liste des tableaux
Tableau 1
Nombre de cohortes = 6, t = 1
Tableau 2
Nombre de cohortes = 6, t = 2
Tableau 3
Résultats d’estimation en panel (N = 5 000, t = 2)
Tableau 4
Résultats d’estimation en pseudo-panel tronqué à 5 %
Tableau 5
Résultats d’estimation en pseudo-panel tronqué à 10 %
Tableau 6
Résultats d’estimation en pseudo-panel tronqué à 20 %
Tableau 7
Nombre de cohortes = 8, t = 1
Tableau 8
Nombre de cohortes = 8, t = 2
Tableau 9
Nombre de cohortes = 12, t = 1
Tableau 10
Nombre de cohortes = 12, t = 2











 10.7202/602194ar
10.7202/602194ar