Résumés
Résumé
Une méthode d’éléments finis mixte hybride est appliquée pour l’approximation de l’écoulement associé au transport en milieu poreux non saturé. Le développement de ce modèle s’effectue dans le cadre du projet européen ARWET, lequel a pour objectif l’étude de nouvelles potentialités de dissipation des pesticides dans les zones humides. La formulation du modèle bidimensionnel est fondée sur les propriétés de l’espace de Raviart-Thomas. L’écueil numérique que posent les problèmes à convection dominante est surmonté par l’introduction d’un limiteur de flux alors qu’un limiteur de pente est généralement utilisé dans la littérature. Le limiteur suggéré est inconditionnellement stable et permet de conserver la précision des résultats à nombre de Peclet élevé.
Mots clés:
- zone humide artificielle,
- éléments finis hybrides,
- modelisation,
- pesticides,
- transport de soluté,
- limiteur de flux
Abstract
A mixed hybrid finite element method was applied to obtain a numerical approximation of the flow and associated transport equations in unsaturated media. The model was developed under the framework of the European Life Environment project ARTWET, which aims to study new treatment potentials for the mitigation of non-point source pesticide pollution in a constructed wetland. The model formulation used is based on Raviart-Thomas space properties, considering a two-dimensional domain divided into triangular elements. In order to control for the difficulties when convection is the dominant process, a flux limiting tool was introduced, although a slope limiter is generally used in the literature. The suggested flux limiting tool makes it possible to preserve precision and unconditional stability at low and very high Peclet numbers.
Keywords:
- Constructed wetland,
- mixed hybrid finite element,
- modelling,
- pesticides,
- solute transport,
- flux limiter
Corps de l’article
1. Introduction
La remédiation des pesticides dans les zones humides artificielles prend en compte les processus biologiques (dégradation biologique, consommation par les plantes et organismes aquatiques), chimiques (précipitation chimique, photo-décomposition et dégradation) et physique (volatilisation, sorption/désorption) (Dordio, 2007). Les résultats obtenus par Schulzet al. (2003) suggèrent que les zones humides végétalisées contribuent fortement à la dissipation du risque de pollution des pesticides en milieu aquatique.
Depuis les années 1970, les problèmes de transport de soluté et de migration des contaminants dans les sols poreux ont reçu une attention croissante dans la littérature. De nombreuses approches de modélisation liées à la biorémédiation et à d’autres applications environnementales ont été développées (Abriolaet al., 1985; Adenekanet al., 1993; Corapcioglu et al., 1987; Forsyth, 1994).
En dépit des progrès continus tant dans le développement des algorithmes et des outils physiques de calcul dans les dernières années, la modélisation des processus couplés d’écoulement, de transport et de migration chimique demeure un challenge mathématique. Il existe toujours des points non résolues ou des limitations avec des approches numériques courantes. L’une des difficultés actuelles est le problème de diffusion numérique induit par des problèmes à advection dominante. Afin de surmonter ces problèmes, des travaux de recherche ont porté sur le developpement de schémas TVD ou de limiteur de flux appliqué avec des succès variés (Forsyth et al., 1998; Liuet al., 2004; Oldenburget al., 2000; Ungeret al.,1996).
Ce papier constitue le volet numérique des travaux sur un bassin d’orage situé au pied d’une colline consacrée à la culture de la vigne. Ce bassin recueille les eaux de surface qui ruissellent sur le bassin versant qui se situe en amont et permet ainsi l’accumulation des sédiments provenant des parcelles cultivées. En conséquence, il y a formation d’une matrice poreuse.
Pour avoir une meilleure compréhension de l’hydro-dynamique et du devenir des pesticides sur ce site, un modèle numérique bidimensionnel est développé afin de simuler le transport en lien avec la dégradation dans la matrice poreuse. Le choix d’un modèle 2D se justifie par la nécessité de prendre en compte les hétérogénéités dans le milieu et celles des conditions initiales telles que la teneur en eau et les concentrations locales très élevées en surface. Un accent particulier sera mis sur la mise en oeuvre d’un limiteur de flux apportant une contribution aux problèmes à advection dominante.
Dans un travail de recensement, de description et comparaison de modèles, Siimes et Kämäri (2003) identifient 82 modèles de transport de soluté et de pesticides disponibles dans le but de choisir le modèle le mieux adapté pour la simulation du devenir des herbicides pour des conditions spécifiques (Finnish conditions). Ce n’est pas l’objectif du présent papier, toutefois le lecteur intéressé peut se référer aux données compilées de CAMASE (1996) et REM (2007). Ils y trouveront des informations concernant l’application et la validation des modèles, aussi bien que l’évaluation de leur performance. Parmi ces travaux, Vinket al. (1997) étudient le transport non saturé du nématicide aldicarb et de l’herbicide simazine dans un sol argileux. Une analyse comparative impliquant les modèles VARLEACH 2.0, LEACHP 3.1, PESTLA 2.3, MACRO 3.1 et SIMULAT 2.4 est réalisée. Ils parviennent à la conclusion qu’aucun des modèles ne décrit la percolation et le lessivage des pesticides avec satisfaction. Après une période de dix mois d’expérimentation, Pestla et Simulat se sont révélés les mieux adaptés. Dans une autre revue, Garrattet al. (2003) comparent la capacité de sept modèles à prédire la propagation de l’aclonifen et de l’ethoprophos dans un sol arable. Les modèles testés sont : VARLEACH, LEACHP, PESTLA, MACRO, PRZM, PELMO, et PLM. Ils observent des différences significatives dans la prévision de leur mobilité et de leur persistance; différences principalement attribuées aux choix des modèles d’écoulement, d’évolution de température et des cinétiques de dégradation. Ils suggèrent qu’un effort considérable est toujours nécessaire dans la paramétrisation des modèles.
Il est donc assez difficile ou rare de trouver des modèles qui donnent entière satisfaction aux utilisateurs sur l’approximation de l’écoulement, le transport et la dégradation. Certains auteurs suggèrent que la mise en oeuvre d’un processus biologique bien adapté peut surmonter le déficit d’un concept d’écoulement assez simple (Gottesbürenet al., 1994 dans Vink, 1997; Seatm et Boesten, 1991). Une affirmation qui n’est pas partagée par Holvoet (2004) qui affirme que la première étape de la modélisation des pesticides est le développement d’un modèle hydrodynamique convenable. Nous avons choisi pour cela d’optimiser le calcul de l’hydrodynamique et du transport par la méthode des éléments finis mixtes hybrides et de traiter les problèmes liés aux nombres de Peclet élevés.
2. Formulation du modèle
L’hydrodynamique dans la matrice poreuse du bassin d’orage est simulée par l’application de l’équation de Richards (1). Cette formulation décrit physiquement l’écoulement dans un milieu poreux variablement saturé.
où:
W(x,z,t) est le terme puits/source [T‑1],
x et z (vertical) sont les cordonnées spatiales [L],
t le temps [T],
C(h) la capacité capillaire [L‑1],
K la conductivité hydraulique [LT‑1],
h la pression en eau du sol [L].
Le transport des pesticides est décrit par l’équation classique d’advection-dispersion (2) avec la présence d’un terme puits/source qui tient compte de la partie dégradation.
où:
f(C,t) est le terme puits/source [ML‑3T‑1],
C la concentration du pesticide dans la phase aqueuse [ML‑3],
S la concentration du pesticide dans la phase solide [ML‑3],
ρ la masse volumique du sol [ML‑3],
t le temps [T],
 le flux surfacique [LT‑1],
le flux surfacique [LT‑1],D le tenseur de dispersion [L2T‑1],
et θ la teneur en eau volumique [L3L‑3].
Les éléments finis mixtes hybrides (EFMH) constituent la méthode numérique utilisée pour la résolution de ces équations. Cette technique est particulièrement bien adaptée pour la simulation des milieux hétérogènes (Moséet al., 1994; Youneset al., 1999). Elle a été appliquée lors des travaux précédents, principalement pour des écoulement en milieu poreux hétérogène saturé. Dans un milieu poreux non saturé, l’hétérogénéité est due à la distribution hétérogène des sédiments et à la non-uniformité des teneurs initiales en eau. L’originalité de ce papier réside dans le fait de simuler l’écoulement et le transport en milieu non saturé à l’aide des EFMH.
2.1 Modèle hydrodynamique bidimensionnel (2D)
Un domaine Ω bidimensionnel (2D) est défini, et la discrétisation spatiale effectue à l’aide d’éléments triangulaires K. L’approximation du flux de Darcy ![]() se fait sur chaque élément par un vecteur
se fait sur chaque élément par un vecteur ![]() appartenant à l’espace de Raviart Thomas d’ordre zéro (Raviart et Thomas, 1977). Sur chaque élément, ce vecteur a les propriétés suivantes :
appartenant à l’espace de Raviart Thomas d’ordre zéro (Raviart et Thomas, 1977). Sur chaque élément, ce vecteur a les propriétés suivantes : ![]() est constant dans chaque élément K,
est constant dans chaque élément K, ![]() est constant sur chaque facette Ei du triangle,
est constant sur chaque facette Ei du triangle, ![]() , où
, où ![]() est le vecteur normal unitaire extérieur à la facette Ei.
est le vecteur normal unitaire extérieur à la facette Ei. ![]() est parfaitement déterminé par la connaissance du flux à travers les facettes (Chavent et Roberts, 1991). En outre, la composante normale de
est parfaitement déterminé par la connaissance du flux à travers les facettes (Chavent et Roberts, 1991). En outre, la composante normale de ![]() est continue de l’élément K à l’élément adjacent K’ et
est continue de l’élément K à l’élément adjacent K’ et ![]() est calculée avec l’aide des vecteurs de bases
est calculée avec l’aide des vecteurs de bases ![]() . Ces vecteurs sont définis par
. Ces vecteurs sont définis par ![]() ,
, ![]() , où δij est le symbole de Kronecker. En conséquence, ces fonctions correspondent au vecteur
, où δij est le symbole de Kronecker. En conséquence, ces fonctions correspondent au vecteur ![]() possédant un flux unitaire à travers la facette Ei, et nul à travers les autres facettes :
possédant un flux unitaire à travers la facette Ei, et nul à travers les autres facettes :
avec QK,Ej le flux d’eau à travers la facette Ej de l’élément K.
La conductivité hydraulique est représentée par le tenseur ![]() , où à travers chaque élément K, kK est la fonction de conductivité hydraulique en milieu non saturé donnée par l’équation modifiée de Mualem-van Genuchten expression (Ippischet al., 2006), KAK est un tenseur anisotropique adimensionnel.
, où à travers chaque élément K, kK est la fonction de conductivité hydraulique en milieu non saturé donnée par l’équation modifiée de Mualem-van Genuchten expression (Ippischet al., 2006), KAK est un tenseur anisotropique adimensionnel.
2.2 Modélisation du transport (une nouvelle approche)
S’agissant de l’équation de transport, nous utilisons une formulation nouvelle, ![]() où
où ![]() est le flux de Darcy [LT‑1] donné par (3). L’approximation du flux convectif dispersif dans chaque élément se fait par un unique vecteur
est le flux de Darcy [LT‑1] donné par (3). L’approximation du flux convectif dispersif dans chaque élément se fait par un unique vecteur ![]() appartenant à l’espace de Raviart-Thomas d’ordre zéro. En conséquence,
appartenant à l’espace de Raviart-Thomas d’ordre zéro. En conséquence, ![]() est constant à travers l’élément K, et est constant sur chaque facette Ei,
est constant à travers l’élément K, et est constant sur chaque facette Ei, ![]() .
. ![]() est parfaitement déterminé par la connaissance du flux de transport à travers chaque facette (4).
est parfaitement déterminé par la connaissance du flux de transport à travers chaque facette (4).
avec Qadv-dispK,Ej le flux advectif-dispersif à travers la facette Ej appartenant à l’élément K et dont la formulation est donnée ci-dessous :
avec:
CK la concentration moyenne de l’élément K,
TCK,Ej la concentration moyenne de la facette Ej.
BK une matrice symétrique (3*3) définie ci-dessous.
DK est le tenseur de dispersion dont les composantes sont données par :
avec:
Dm le coefficient de diffusion moléculaire [L2 T‑1],
αL la dispersivité longitudinale de la matrice solide [L],
αT la dispersivité transversale de la matrice solide [L],
qi, qj les composantes du flux de Darcy q [LT‑1],
θ la teneur en eau volumique du sol [L3L‑3].
δi,j le symbole Kronecker [-]
Appliquant à l’équation 2 la méthode implicite d’Euler pour la discrétisation temporelle et une approximation des grandeurs à chaque élément K, il suit :
avec ![]() et
et ![]() l’isotherme d’adsorption linéaire.
l’isotherme d’adsorption linéaire.
Ensuite, des expressions 4 et 5 l’équation 9 est déduite ci‑dessous :
où ![]() .
.
Substituant (9) dans (8) et considérant une masse volumique constante, nous obtenons :
Multiplions l’équation 10 par λK / αK et procédons à un réarrangement des termes, l’équation 11 ci-dessous est déduite :
où: ![]()
Notons ![]() ;
;
puis ![]()
La concentration moyenne de chaque élément K est estimée par l’expression ci-dessous :
L’équation de continuité (13) est écrite pour toute les facettes intérieures Ei (∀i = 1,2,3) du domaine Ω. La facette Ei est commune aux éléments K et K’.
Suivant une procédure similaire bien décrite spécifiquement pour l’hydrodynamique par plusieurs auteurs (Belfort, 2006; Moséet al., 1994; Nayagum, 2001) les équations 12 et 13 permettent l’écriture de la formulation mixte hybride pour l’équation de transport. Les lecteurs peuvent se référer à ces auteurs pour les transformations matricielles.
2.3 Control des oscillations pour un problème à advection dominante – définition d’un limiteur de flux
De nombreux modèles d’écoulement et de transport en milieux poreux partiellement saturés sont confrontés au problème d’advection dominante qui induit des oscillations instables. Dans la littérature, les auteurs recourent à la technique d’opérateurs de spliting. Les EFMH sont appliqués pour la résolution du terme dispersif de l’équation de transport, alors que la méthode des éléments finis discontinue est appliquée pour le terme convectif; avec un limiteur de pente qui permet de réduire les oscillations (Ackereret al., 1999; Hoteitet al., 2002; Hoteitet al., 2004; Mazzia et al., 2002; Oltean et Buès, 2001; Siegelet al., 1997). D’après Carrayrouet al. (2005), chaque méthode introduit une erreur intrinsèque dans la solution.
Dans cet article, une nouvelle formulation pour la résolution de l’équation de transport est introduite. Comme mentionnée plus haut, une approche globale (avec l’approximation des EFMH) est utilisée. Les oscillations issues du problème à convection dominante seront contrôlées par l’usage d’un limiteur de flux spécifique aux EFMH.
L’équation 5 donnant le flux par facette est centrée sur l’élément K; c’est le résultat d’un second ordre de discrétisation. Introduisant une constante η, l’ordre de discrétisation du terme d’advection décroît en fonction de la direction du flux à travers les facettes. La nouvelle expression du flux par facette est donnée ci-dessous; elle permet pour différentes valeurs de η, l’obtention d’un schéma inconditionnellement stable.
• Si ![]() <0
<0
• Si ![]() >0
>0
Toutes les équations impliquant le flux doivent être modifiées en tenant compte de l’équation 14.
2.4 Adsorption et dégradation
De nombreux modèles cinétiques de biodégradation dans les sols sont proposés dans la littérature. À ce sujet, une étude fondamentale a été développée par Alexander et Scow (1989), elle propose neuf formulations fondées sur le couplage des cinétiques de Monod et celles de Michaelis-Menten et qui dépendent de la densité de la population bactérienne active et celle du substrat organique. Les croissances linéaires, logistiques et exponentielles de la biomasse sont ainsi distinguées. Les profils types de disparition du substrat en fonction du temps sont alors proposés. Les choix de modélisation permettant la prise en compte des hétérogénéités rend possible la détermination des concentrations de substrat sur un profil quelconque de sol. Ce travail sera proposé dans les recherches futures.
2.5 Solution numérique
La discrétisation de l’équation de Richards, puis sa linéarisation par la méthode de Picard, conduit à un système d’équations linéaires, où les inconnues sont les traces de pression (Th) sur les facettes. Le nombre d’inconnues est égal au nombre de facettes à pression non imposées. Par analogie, les traces de concentration sur les facettes sont les inconnues du système linéaire issu de l’équation macroscopique de transport.
Les matrices associées à ces équations sont symétriques et définies positives. En conséquence, elles sont résolues par la méthode du gradient préconditionné. Le processus d’itération est stoppé lorsque la norme résiduelle relative est inférieure à la tolérance prédéterminée par l’utilisateur :
avec:
nf, le nombre de facettes dans le domaine Ω de l’écoulement;
Th, le vecteur trace de pression des différentes facettes du domaine Ω;
TC, le vecteur trace de concentration des différentes facettes du domaine Ω;
n, l’indice de temps;
m, l’indice d’itération;
τH et τT sont les critères de tolérance pour l’hydrodynamique et le transport respectivement.
2.6 Control du pas de temps
L’ajustage du pas de temps (Δt) se calcule automatiquement d’après les règles ci-dessous :
Un pas de temps minimal et maximal est fixé (Δtmin et Δtmax), ils sont spécifiés par l’utilisateur. À tout instant : Δtmin ≤ Δt ≤ Δtmax.
-
Le nombre adimensionnel de Fourrier (rapport du nombre de Courant-Friedrichs-Lewy (Co) et du nombre de Peclet (Pe)) permettent de fixer l’incrément maximal du pas de temps par le billet de l’inégalité ci-après :

où:

et Vx ,Vz la vitesse intersticielle des les pores dans les directions x et z respectivement (LT‑1);
∆x , ∆z les dimensions d’une maille dans les directions x et z respectivement (L);
Dxx, Dzz, Dxz les coefficients de dispersion (L2 T‑1).
Ci-dessous, pour chaque élément K, l’incrément maximal de temps est :
Le pas de temps maximal pour le transport (∆t maxtransport) serait le minimun des ∆t maxK. Par analogie, le pas de temps maximal permis pour l’hydrodynamique (∆t maxhydrodynamics) est déterminé en utilisant une règle similaire et en remplaçant, d’une part, le coefficient de dispersion par le paramètre D(h) (diffusivité de l’humidité dans le sol), et, d’autre part, la vitesse intersticielle des pores par v(h) (vitesse de l’écoulement). Ils sont donnés par ces fonctions :
où: ![]() est la capacité capillaire du sol, et u une variable définie par les transformations de Kirchhoff (El-Kadi et Ling, 1993).
est la capacité capillaire du sol, et u une variable définie par les transformations de Kirchhoff (El-Kadi et Ling, 1993).
L’incrément de temps ne doit donc pas excéder la valeur minimale de ∆t maxhydrodynamics et ∆t maxtransport.
Le pas de temps initial ∆t serait égal à la valeur minimale entre ∆t maxhydrodynamics et ∆t maxtransport. Pour les pas de temps suivants, une méthode heuristique (Belfort, 2006; Šimuneket al., 2005) est utilisée avec toujours le respect des règles 1 et 2.
3. Résultats et discussion
3.1 Cas test en monodimensionnel
Un cas test unidimensionnel (une seule maille sur l’axe horizontal) est proposé dans le but de mesurer les performances du modèle. Il consiste en une infiltration dans une colonne de sol (L = 100 cm) non saturé. Les paramètres spécifiques du sol sont donnés au tableau 1, où : θr et θs sont respectivement les teneurs en eau résiduelle et à saturation; Ks est la conductivité hydraulique à saturation, α est un paramètre de fitting, n et m sont des paramètres liés à la distribution de la taille des pores, he est la valeur d’entrée d’air (Ippisch, 2006).
Tableau 1
Paramètre du sol Glendale (Kirkland, 1992).
Glendale clay loam soil parameter.
θr |
θs |
Ks (cm/d) |
α (cm‑1) |
n |
he (cm) |
|---|---|---|---|---|---|
0,1060 |
0,4686 |
13,1 |
0,0104 |
1,3954 |
0 |
Les conditions initiales et aux limites pour l’hydrodynamique et le transport sont données au tableau 2. Les coefficients de dispersivité longitudinale et transversale sont égaux et valent 10 cm.
Tableau 2
Conditions initiales et aux limites du cas test monodimensionnel.
Initial and Boundary Conditions for the one-dimensional test case.
Conditions |
Hydrodynamique |
Transport |
|---|---|---|
Initiales |
h(0 ≤ z ≤ 100 cm, t = 0) = ‑200 cm |
C(Z ≠ 0, t = 0) = 0,1 g•L‑1 |
Limites |
q(z = 0,t ≥ 0) = 8,64 cm•j‑1 |
C(z = 0,t ≥ 0) = 1,0 g•L‑1 |
3.1.1 Vérification de l’hydrodynamique
Les résultats commentés sont obtenus après un temps d’infiltration de 0,25 jour et comparés à ceux obtenus dans les mêmes conditions à l’aide d’Hydrus (Šimuneket al., 2005), logiciel de simulation très utilisé par les spécialistes et non spécialistes de l’écoulement, du transport et transfert réactif en milieu variablement saturé. La figure 1 illustre l’effet d’un incrément automatique du pas de temps et d’un pas de temps constant sur l’évolution du front hydrodynamique. Les approximations de l’écoulement obtenues par l’application Hydrus (pas de temps initial : 1,1974 x 10‑3 j) et les EFMH utilisant un pas de temps adaptatif (3 116 pas de temps : 1,1974 x 10‑3 j ≥ ∆T≥ 1,2195 x 10-5 j) sont similaires. En dépit du fait qu’il soit possible d’obtenir une bonne approximation de l’écoulement en moins de pas de temps avec un incrément constant (250 pas de temps: ∆T = 1,00 x 10‑3 j), le choix d’un pas de temps adaptatif a été fait. Bien que le nombre de pas de temps et donc le temps de simulation du processeur soit plus élevé dans ce cas, l’approximation du transport est plus précise (Figure 1).
Figure 1
Effet du pas de temps sur l’hydrodynamique (gauche) et sur le transport (droite).
Effect of the time step on hydrodynamics (left) and transport (right).
Un choix inadéquat du pas de temps peut conduire à une approximation précise du calcul de l’hydrodynamique mais moins précise s’agissant du transport (Figure 1).
3.1.2 Vérification du transport unidimensionnel
Le modèle a été testé pour différentes valeurs de dispersivité (αL = αT). L’intérêt du limiteur de flux introduit lorsque l’advection est dominante (nombre de Peclet élévé) est observé dans la figure 2. Pour ces cas testés, le paramètre de pondération η = 0,5. L’effet de l’augmentation du nombre de Peclet est illustré à la fois dans les mailles et sur les facettes. La correction effectuée par le limiteur de flux suggéré est appréciable.
Figure 2
Correction du limiteur de flux pour différent Pe.
Effect of the flux limiter for different Peclet numbers.
a)
Dispersivité 10 cm, Pe max = 1,02
b)
Dispersivité 1 x 10‑2 cm, Pe max = 1,02 x 10‑3
c)
Dispersivité 1 x 10‑6 cm, Pe max = 1,02 x 10‑7
À faible nombre de Peclet (Figure 2a), les résultats obtenus par les EFMH dans les mailles et les facettes présentent une très étroite proximité comparés à ceux obtenus par Hydrus. Dans ce cas, les résultats sont indépendants de l’utilisation du limiteur de flux.
À nombre de Peclet élevé (Figure 2b), les oscillations sont observées sur le calcul des traces de concentration sur les facettes sans limiteur de flux ainsi qu’avec Hydrus et les concentrations dans les mailles décrochent. Une différence notable de concentration apparaît ainsi dans le barycentre des mailles et sur les facettes avoisinantes.
Lorsque Pe → ∞ (Figure 2c), l’approximation des concentrations dans les mailles demeure relativement constante et égale à la concentration initiale.
Dans tous ces cas, les oscillations sont entièrement inhibées grâce à l’usage du limiteur de flux. En conséquence, le limiteur de flux suggéré confère une précision et une stabilité inconditionnelle à faible nombre de Peclet et une stabilité inconditionnelle à nombre de Peclet très élevé. La précision à nombre de Peclet très élevé n’a pu être appréciée du fait de la non-convergence de l’application Hydrus. Une analyse de sensibilité est menée dans la suite afin d’évaluer l’influence du paramètre η.
3.1.3 Analyse de sensibilité du limiteur de flux
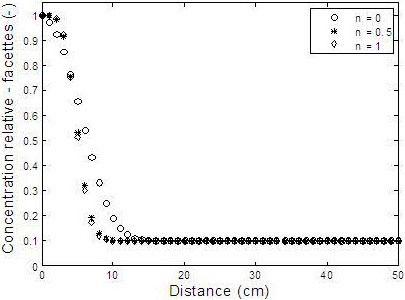
η est un paramètre de pondération de la partie advective et dispersive du flux à travers les facettes. Comme précisé plus haut, le calcul des concentrations est indépendant de l’implémentation du limiteur de flux à faible Pe (Figure 2a). En conséquence, l’effet de l’application du limiteur de flux est donc lié à Pe. La figure 3 montre les concentrations sur les facettes obtenues pour différentes valeurs de η, lorsque Pemax = 10,2, Pemax = 1,02 x 103, et Pemax = 1,02 x 106. Les concentrations demeurent relativement insensibles lorsque η prend les valeurs de 0,5 à 1,0 : des résultats stables et identiques sont obtenus pour ces valeurs. Lorsque η = 0, l’effet de diffusion numérique est très significatif avec l’augmentation de Pe. En effet, d’après l’équation 8, la composante du flux de transport au barycentre de chaque maille est pondérée par la même valeur (0,5) que celle calculée sur la facette amont lorsque η = 0, dans tous les autres cas la facette amont a un facteur de pondération plus élevé.
Figure 3
Sensibilité du paramètre de pondération.
Weighing parameter sensitivity.
a)
Pe max = 1,02 x 101
b)
Pe max = 1,02 x 103
c)
Pe max = 1,02 x 106
3.2 Cas test bidimensionnel (2D)
Un cas test de transport de soluté en milieu saturé est traité dans la suite. Les concentrations initiales sont nulles dans tout le domaine. Le domaine de discrétisation et les conditions aux limites sont présentés dans la figure 4.
Figure 4
Domaine bidimensionnel (gauche) et maillage régulier (droite).
Two dimensional convection-dispersion domain (left) and regular mesh (right).
3.2.1 Vérification du modèle de transport en 2D
Dans l’objectif de tester les performances du modèle, ce problème bidimensionnel est résolu pour des nombres Peclet élevés. Les solutions sont obtenues après un temps de simulation de 20 jours. Les paramètres utilisés sont reportés au tableau 3. Les résultats numériques sont comparés aux solutions analytiques de Leij Feike et Dane (1990) dans Siegel (1995).
Tableau 3
Paramètres des cas tests simulés.
Parameters used in various cases.
Cas |
Vx (m•j‑1) |
Vy (m•j‑1) |
αL (m2•j‑1) |
αT (m2•j‑1) |
Δx (m) |
Δy (m) |
Pe |
|---|---|---|---|---|---|---|---|
1 |
1,0 |
0,0 |
1,0 |
0,1 |
1,0 |
1,0 |
0,91 |
2 |
1,0 |
0,0 |
0,1 |
0,01 |
0,5 |
1,0 |
7,14 |
3 |
1,0 |
0,0 |
1 x 10‑5 |
1 x 10‑6 |
0,5 |
1,0 |
7,14 x 104 |
Les profils de concentration sont numériquement calculés au centre des mailles alors que les solutions analytiques sont obtenues aux noeuds du domaine.
Le premier cas test considère un faible nombre de Peclet (Pe > 2 : le problème n’est pas à advection dominante). Les lignes d’iso-concentration obtenues à l’aide des EFMH (sans limiteur de pente) sont en accord avec la solution analytique (Figures 5a et 5b).
Figure 5
Lignes d’iso-concentration : Cas test 1.
Iso-concentration lines: Test case 1.
a)
EFMH solution numérique
MHFE numerical solution
b)
Solution analytique
Analytical solution
Le second cas test (Pe = 7,1, problème à advection dominante) illustre le fait qu’en l’absence de limiteur de flux, des résultats instables et peu précis sont obtenus. L’approximation des EFMH, en comparaison aux solutions analytiques, est qualitativement améliorée avec application du limiteur de flux (Figures 6a, 6b et 6c).
Figure 6
Lignes d’ iso-concentration : Cas test 2.
Iso-concentration lines: Test case 2.
a)
EFMH sans limiteur de flux
MHFE without flux limiting
b)
EFMH avec limiteur de flux, η = 1
MHFE with flux limiting
c)
Solution analytique
Analytical solution
Lorsque le nombre de Peclet est très élevé (Pe = 7,14 x 104), les résultats obtenus en abaissant l’ordre de discrétisation du flux de transport sont stables et épousent très bien les solutions analytiques (Figures 7a, 7b, 7c).
Figure 7
Lignes d’iso-concentration : Cas test 3.
Iso-concentration lines: Test case 3.
a)
EFMH sans limiteur de flux
MHFE without flux limiting
b)
EFMH avec limiteur de flux, η = 1
MHFE with flux limiting
c)
Solution analytique
Analytical solution
Les résultats ci-dessus obtenus montrent que le modèle developpé est un bon outil numérique pour l’approximation bidimensionnelle du transport en milieu poreux saturé. En outre, les performances du limiteur de flux sont satisfaisantes.
4. Conclusion
Les potentialités que peuvent développer les zones humides artificielles dans l’atténuation de la pollution due aux pesticides, d’origine agricole, sont actuellement étudiées dans le cadre du projet européen Artwet. La simulation de la dynamique des pesticides dans un profil de sol pouvant faciliter un contrôle environnemental revêt un aspect non négligeable du projet.
L’objectif de ce travail était de présenter une nouvelle formulation pour simuler l’écoulement, le transport réactif dans un milieu poreux variablement saturé par l’application de la méthode d’éléments finis mixtes hybrides. Une approche globale à laquelle est associé un limiteur de flux est utilisée.
Les oscillations numériques dues aux processus de transport à advection dominante sont contrôlés avec succès grâce à l’implémentation d’un limiteur de flux. Cette technique constituerait une alternative à l’usage de la séparation d’opérateur très souvent couplé à un limiteur de pentes.
La vérification du modèle s’opère à travers la simulation des problèmes mono dimensionnel ou bidimensionnels. Les approximations numériques des cas testés sont comparés à ceux obtenus par l’application Hydrus ou des solutions analytiques. Ainsi, des résultats satisfaisants illustrent la capacité du modèle à décrire l’hydrodynamique et le transport réactif en milieu non saturé. L’usage du limiteur de flux rend possible l’obtention de solutions précises et inconditionnellement stables à nombres de Peclet élevés.
La discrétisation temporelle joue un rôle capital durant la simulation. Une sélection inadéquate du pas de temps peut permettre une approximation précise de l’hydrodynamique alors qu’elle est moins précise pour le transport.
Les travaux futurs permettront d’améliorer le limiteur de flux en définissant un critère permettant l’usage du paramètre de pondération η seulement lorsque la diffusion est localisée ainsi qu’une comparaison avec d’autres limiteurs de flux et des limiteurs de pente.
Parties annexes
Remerciements
Le projet Artwet dans le cadre où s’inscrit cet article est financé par la Commission européenne, la Région Alsace (France), les Conseils Généraux (Haut Rhin, Indre et Loire; France), l’Agence de l’Eau Loire Bretagne (France). Nous remercions la mairie de Rouffach (Alsace, France) et le Lycée agricole et viticole de Rouffach pour leur implication dans le projet.
Références bibliographiques
- Abriola L.M. et G.F. Pinder (1985). A multiphase approach to the modeling of porous media contamination by organic compounds, 1. Equation development. Water Resour. Res., 21, 11–18.
- Ackerer Ph., A. Younes, R. Mose (1999). Modeling variable density flow and solute transport in porous medium: 1. Numerical model and verification. Transport Porous Media., 35, 345-373.
- Adenekan A.E., T.W. Patzek et K. Pruess (1993). Modeling of multiphase transport of multicomponent organic contaminants and heat in the subsurface: Numerical model formulation. Water Resour. Res., 29, 3727–3740.
- Alexander M. et M. Scow (1989). Kinetics of biodegradation in soil. pp. 243-269. Dans : Reactions and movement of organic chemicals in soils, Sawhney B.L. et Brown K, (Éditeurs), SSSA Spec. Publ. 22. SSSA Madison, WI, USA.
- Belfort B. (2006). Modélisation des écoulements en milieux poreux non saturés par la méthode des éléments finis mixtes hybrides. Thèse de Doct., Univ. Louis Pasteur. Strasbourg, France, 220 p.
- Camase (1996). Register of agro-ecosystems models. Dans : Camase: Concerted Action for the Development and Testing of Quantitative Methods for Research on Agricultural System and the Environment. Plentinger M.C. et Penning de Vries F.W.T. (Éditeurs). DLO Research Institute for Agrobiology and Soil Fertility, Wageningen, the Netherlands, 420 p.
- Carrayrou J., R. Mosé et P. Behra (2004). Operator-splitting procedures for reactive transport and comparison of mass balance errors. J. Contam. Hydrol., 68, 239-268.
- Chavent G et JE. Roberts (1991). A unified physical presentation of mixed, mixed-hybrid finite elements and standard finite difference approximations for the determination of velocities in waterflow problems. Adv. Water Resour., 14, 329-348.
- Corapcioglu M.Y. et A.L. Baehr (1987). A compositional multiphase model for groundwater contamination by petroleum products, 1. Theoretical considerations. Water Resour. Res., 23, 191–200.
- Dordio A.V., J. Teimão, I. Ramalho, A.J. Palace Carvalho et A.J. Estêvão Candeias (2007). Selection of a support matrix for the removal of some phenoxyacetic compounds in constructed wetlands systems. Sci. Total Environ., 380, 237-246.
- El-Kadi A.I. et G. Ling (1993). The Courant and Peclet number criteria for the numerical solution of the Richards equation. Water Resour. Res., 29, 3485-3494.
- Forsyth P.A. (1994). Three-dimensional modeling of steam flush for DNAPL site remediation. Int. J. Num. Methods Fluids, 19, 1055–1081.
- Forsyth P.A., A.J.A. Unger et E.A. Sudicky (1998). Nonlinear iteration methods for nonequilibrium multiphase subsurface flow. Adv. Water Resour., 21, 433499.
- Garratt J.A., E. Capri, M. Trevisan, G. Errera et R.M. Wilkins (2003). Parameterisation, evaluation and comparison of pesticide leaching models to data from a Bologna field site, Italy. Pest. Manag. Sci., 59, 3-20.
- Gottesbüren B., W. Pestemer et S. Beulke (1994). Characteristics and effects of the time course of the sorption behaviour of herbicides in soil (in German). Zeitschrift für Pflanzenkrankheiten und Pflanzenschutz, Sonderheft., XIV, 661-670.
- Holvoet K., A. van Griensven, P. Seuntjens, P.A. Vanrolleghem (2004). Hydrodynamic modelling with soil and water assessment tool (SWAT) for predicting dynamic behaviour of pesticides. 211-218. Dans : Water and Environment Management Series. Young Researches 2004, Lens P. et R. Stuetz, (Éditeurs). ISBN: 1843395053.
- Hoteit H., Ph. Ackerer, R. Mosé, J. Erhel et B. Philippe (2004). New two-dimensional slope limiters for discontinuous Garlerkin methods on arbitrary meshes. Int. J. Numer. Meth. Eng., 61, 2566-2593.
- Hoteit H., J. Erhel, R. Mosé, B. Philippe et Ph. Ackerer (2002). Numerical reliability for mixed methods applied to flow problems in porous media. Comput. Geosci., 6, 161-194.
- Ippisch O., H.J. Vogel et P. Bastian (2006). Validity limits for the van Genuchten-Mualem model and implications for parameter estimation and numerical simulation. Adv. Water Resour., 29, 1780-1789.
- Kirkland M.R., R.G. Hills et P.J. Wierenga (1992). Algorithms for solving Richards’ equation for variably saturated soils. Water Resour. Res., 28, 2049-2058.
- Oldenburg C.M. et K. Pruess (2000). Simulation of propagating fronts in geothermal reservoirs with the implicit Leonard total variation diminishing scheme. Geothermics, 29, 1–25.
- Oltean C. et M.A. Buès (2001). Coupled groundwater flow and transport in porous media. A conservative or non-conservative form? Transp. Porous Media, 44, 219-246.
- Leij F.J. et J.H. Dane (1990). Analytical solutions of the one-dimensional advection equation and two- or three-dimensional dispersion equation. Water Resour. Res., 26, 1475–1482.
- Liu J., M. Delshad, G.A. Pope et K. Sepehrnoori (2004). Application of higher-order flux-limited methods in compositional simulation. Transp. Porous Media., 16 1–29.
- Mazzia A., L. Bergamaschi, C.N. Dawson et M. Putti (2002). Godunov mixed methods on triangular grids for advection-dispersion equations. Comput. Geosci., 6, 123-139.
- Mosé R., P. Siegel, P. Ackerer et G. Chavent (1994). Application of the mixed hybrid finite element approximation in a groundwater flow model: Luxury or necessity? Water Resour. Res., 30, 3001-3012.
- Nayagum D. (2001). Simulation numérique de la pollution du sous-sol par les produits pétroliers et dérives : Application au cas d’un écoulement diphasique monodimensionnel. Thèse de Doct., Univ. Louis Pasteur, Strasbourg, France, 151 p.
- Raviart P.A. et J.M. Thomas (1977). A mixed finite method for the second order elliptic problems., Dans : Mathematical Aspects of the Finite Element Methods. Galligani I. et Magenes, E., (Éditeurs). Lecture Notes in Math. 606, Springer, New York, pp. 292-315.
- REM (2007). Register of Ecological Models. A meta-database for existing mathematical models in ecology. University of Kassel and National Research Center for Environment and Health (GSF), 2006. http://www.wiz.uni-kassel.de/ecobas.html, consulté le 26 avril 2007.
- Schultz R., M.T. Moore, E.R. Bennett, C.D. Milam, J.L. Bouldin, J.L. Farris, Jr S. Smith et C.M. Cooper (2003). Acute toxicity of methyl-parathion in wetland mesocosms: assessing the influence of aquatic plants using laboratory testing with Hyalella azteca. Arch. Environ. Contam. Toxicol., 45, 331-336.
- SIEGEL P. (1995). Transfert de masse en milieux poreux fortement hétérogènes : modélisation et estimation de paramètres par éléments finis mixtes hybrides et discontinus. Thèse de Doctorat, Univ. Louis Pasteur, Strasbourg, France.
- Siegel P., R. Mosé, Ph. Ackerer et J. Jaffre (1997). Solution of the advection-diffusion equation using a combination of discontinuous and mixed finite elements. Int. J. Numer. Meth. Fluids, 24, 595-613.
- Siimes K. et J. Kämäri (2003). A review of available pesticide leaching models: Selection of models for simulation of herbicide fate in Finnish sugar beet cultivation. Boreal. Env. Res., 8, 31-51. ISSN 1239-6095.
- Šimunek J., M.Th. van Genuchten et M. Šejna (2005). The HYDRUS-1D software package for simulating the movement of water, heat, and multiple solutes in variably saturated media, Version 3.0, HYDRUS Software Series 1, Department of Environmental Sciences, University of California Riverside, Riverside, California, USA, 240 p.
- Unger A.J.A., P.A. Forsyth et E.A. Sudicky (1996). Variable spatial and temporal weighting schemes for use in multi-phase compositional problems. Adv. Water Resour., 19, 1–27.
- van der Zee S.e.a.t.m. et J.J.T.I. Boesten (1991). Effects of soil heterogeneity on pesticide leaching to groundwater. Water Resour. Res., 27, 3051-3063.
- Vink J.P.M., B. Gottesburen, B. Diekkruger et van der Zee S.e.a.t.m. (1997). Simulation and model comparison of unsaturated movement of pesticides from a large clay lysimeter. Ecol. Model., 105, 113-127.
- Younes A., R. Mose, P. Ackerer, G. Chavent (1999). A new formulation of the mixed finite element method for solving elliptic and parabolic PDE with triangular elements. J. Comput. Phys., 149, 148-167.
Liste des figures
Figure 1
Effet du pas de temps sur l’hydrodynamique (gauche) et sur le transport (droite).
Effect of the time step on hydrodynamics (left) and transport (right).
Figure 2
Correction du limiteur de flux pour différent Pe.
Effect of the flux limiter for different Peclet numbers.
a)
Dispersivité 10 cm, Pe max = 1,02
b)
Dispersivité 1 x 10‑2 cm, Pe max = 1,02 x 10‑3
c)
Dispersivité 1 x 10‑6 cm, Pe max = 1,02 x 10‑7
a)
Pe max = 1,02 x 101
b)
Pe max = 1,02 x 103
c)
Pe max = 1,02 x 106
Figure 4
Domaine bidimensionnel (gauche) et maillage régulier (droite).
Two dimensional convection-dispersion domain (left) and regular mesh (right).
a)
EFMH solution numérique
MHFE numerical solution
b)
Solution analytique
Analytical solution
a)
EFMH sans limiteur de flux
MHFE without flux limiting
b)
EFMH avec limiteur de flux, η = 1
MHFE with flux limiting
c)
Solution analytique
Analytical solution
Liste des tableaux
Tableau 1
Paramètre du sol Glendale (Kirkland, 1992).
Glendale clay loam soil parameter.
θr |
θs |
Ks (cm/d) |
α (cm‑1) |
n |
he (cm) |
|---|---|---|---|---|---|
0,1060 |
0,4686 |
13,1 |
0,0104 |
1,3954 |
0 |
Tableau 2
Conditions initiales et aux limites du cas test monodimensionnel.
Initial and Boundary Conditions for the one-dimensional test case.
Conditions |
Hydrodynamique |
Transport |
|---|---|---|
Initiales |
h(0 ≤ z ≤ 100 cm, t = 0) = ‑200 cm |
C(Z ≠ 0, t = 0) = 0,1 g•L‑1 |
Limites |
q(z = 0,t ≥ 0) = 8,64 cm•j‑1 |
C(z = 0,t ≥ 0) = 1,0 g•L‑1 |