Article body

Introduction

Le degré auquel les effets des chocs persistent dans l’économie a fait l’objet d’une imposante littérature qui a fait suite à la contribution majeure de Nelson et Plosser (1982). Cette littérature, basée essentiellement sur des variables macroéconomiques telles le PNB de différents pays de l’OCDE, est surtout marquée par des résultats mitigés qui reflètent essentiellement la difficulté à déterminer les propriétés de long terme de la production agrégée. Une approche alternative serait d’examiner les propriétés ainsi que le degré de persistance des séries chronologiques à un niveau désagrégé.

Malgré les nombreux aspects prometteurs mis en évidence par Romer (1991), l’utilisation de l’approche désagrégée n’a pas eu l’écho qu’elle méritait. L’étude de Pesaran, Pierse et Lee (1993) (ci-après PPL, 1993), effectuée pour les États-Unis, est l’une des rares exceptions. Ces derniers ont développé l’argument de Romer (1991), en montrant, entre autres, que l’information contenue dans les relations entre les taux de croissance de la production sectorielle et dans les corrélations qui existent entre les chocs inattendus dans les taux de croissance de la production sectorielle peut être utilisée opportunément pour obtenir un estimé plus fiable et plus précis de la mesure de persistance de la production agrégée. L’approche désagrégée leur a permis aussi de décomposer la persistance des chocs de la production agrégée et sectorielle en deux composantes : la persistance due aux chocs d’origine macroéconomique et celle due aux chocs spécifiques à certains secteurs.

Le propos de ce travail est double. En premier lieu, il s’agit d’appliquer pour le Canada le cadre analytique développé par PPL (1993), en mettant en évidence la contribution relative des chocs d’origine sectorielle sur la mesure agrégée de la persistance. L’exploitation de cette approche désagrégée s’avère d’autant plus intéressante qu’elle n’a jamais été explorée pour le Canada[1]. Dans ce travail, nous avons identifié explicitement le choc du blé et le choc pétrolier dans un modèle multisectoriel de l’économie canadienne, respectivement pour les périodes d’avant-guerre et d’après-guerre. Les estimés de la persistance sectorielle et de l’ensemble de l’économie canadienne pour les périodes 1870-1914 et 1947-1996 y sont présentés et discutés. Les implications des résultats sur l’interprétation du développement économique du Canada y sont également examinées.

En second lieu, nous examinons si la tendance des chocs à avoir des effets transitoires ou permanents a changé entre les périodes d’avant et d’après-guerre. Un tel exercice n’est pas sans intérêt pour comprendre la nature des chocs et la manière dont les industries y ont fait face. Si les secteurs affichent un même niveau de persistance entre l’avant-guerre et l’après-guerre, ceci suggère que la nature des chocs auxquels font face les secteurs et la manière dont ceux-ci réagissent n’ont pas changé à travers le temps. Si les chocs sont passés d’une nature transitoire à une nature permanente entre l’avant et l’après-guerre, on devrait remarquer alors un changement notable dans la persistance des fluctuations dans les secteurs entre les deux périodes. Dès lors, une hausse de la persistance des productions sectorielles pourrait suggérer que pour ces secteurs les chocs permanents sont devenus plus importants durant la période d’après-guerre ou encore que la capacité des secteurs à faire face à ces chocs a baissé à travers le temps.

Le reste de l’article est ainsi organisé. La première section présente le modèle ainsi que la décomposition de la persistance en deux composantes, l’une associée aux chocs macroéconomiques explicitement identifiés, l’autre associée aux chocs non explicitement identifiés. La deuxième section présente les chocs macroéconomiques qui ont marqué le développement historique du Canada. La troisième section fournit les spécifications économétriques et discute les résultats obtenus. Les principaux résultats, leurs implications sur le développement historique du Canada, ainsi que les extensions possibles de ce travail sont résumés en conclusion.

1. Le modèle

Nous avons retenu, pour notre analyse de la persistance des chocs sur l’économie canadienne, le modèle multisectoriel simplifié des taux de croissance des productions sectorielles utilisé par PPL (1993). Ce modèle prend en compte un seul choc macroéconomique explicitement identifié et des chocs « autres ». Les chocs « autres » regroupent les chocs macroéconomiques indépendants de ceux identifiés explicitement dans l’analyse, et les chocs purement spécifiques aux secteurs.

Soit yit un vecteur (m × 1) du logarithme des productions sectorielles qui peut être représenté par un processus stationnaire linéaire en première différence. Un modèle multisectoriel général de la croissance de la production peut être écrit comme suit :

où α est un vecteur m × 1 de constantes représentant les taux de croissance moyens spécifiques de chaque secteur de l’économie; υt est un vecteur p × 1 d’innovations des variables macroéconomiques xt et εt est un vecteur m × 1 des innovations spécifiques à chaque secteur de moyenne nulle et de matrice de variance Σ = (σij). A(L) et D(L) sont des matrices de polynômes de la forme

où les termes Ai et Di sont, respectivement, des matrices m × m et m × p de coefficients fixes, Ao = Im, et le (i, j)ème élément de A(L) est dénoté par le polynôme de retards aij(L).

Le vecteur des innovations υt est défini comme

où xt est un vecteur p × 1 de variables macroéconomiques, Γ est une matrice p × k de coefficients fixes et zt est un vecteur k × 1 de variables prédéterminées. Cette formulation est très générale et comprend la spécification du vecteur autorégressif comme cas particulier. Les innovations υt sont supposées être des processus bruit blanc de moyenne nulle et de variance constante ψ = (ψij). Ces innovations correspondent aux chocs macroéconomiques tels les changements non anticipés de la production du blé de 1896 et du prix du pétrole en 1973. Les innovations spécifiques au secteur εt représentent la variabilité résiduelle dans Δyt non associée aux p chocs macroéconomiques identifiés, υt. Pour s’assurer que le système (1) soit identifié, nous supposons que υt et εt sont non corrélées (voir PPL, section 3.3).

Le système décrit par (1) fournit des représentations des séries chronologiques de la croissance de la production des m secteurs dont chacun fait l’objet des p chocs « macro » et d’un résidu, vraisemblablement un choc spécifique. La production agrégée Yt est défini par

où w = (w1, w2, ..., wm)′ est un vecteur m × 1 de pondérations fixes. Dans la partie empirique, nous avons posé w = (1, 1, ..., 1)′; ce qui revient à utiliser la somme des logarithmes des productions sectorielles comme mesure de la production agrégée. Bien que cette mesure est différente du logarithme de la somme des productions sectorielles utilisées dans la littérature, nous avons, cependant, trouvé que les deux mesures sont assez proches et présentent des fonctions d’autocorrélation similaires.

Sous la spécification du modèle multisectoriel (1), la croissance de la production agrégée peut être écrite comme :

Notons que même pour des spécifications simples de la croissance univariée de la production, l’équation (3) peut avoir un ordre élevé de représentation ARMA. Ceci pourrait justifier, a priori, l’usage des données désagrégées dans l’analyse de la persistance agrégée, car avec le nombre limité d’observations disponibles, l’estimation d’un ordre élevé du processus ARMA pour la production agrégée peut ne pas être désirable, voire même possible (voir PPL pour une discussion plus élaborée).

Plusieurs statistiques ont été suggérées dans la littérature comme mesures de persistance des modèles univariés. Comme l’ont montré PPL, toutes ces mesures alternatives sont basées sur la fonction de densité spectrale de ΔYt évaluées à la fréquence zéro, fΔY(0), et différentes seulement en termes d’échelle. La mesure de persistance de la production agrégée, PY, dans le modèle multisectoriel (1.1) est basée sur la densité spectrale de ΔYt = w′ Δyt à la fréquence zéro dont l’échelle est fournie par la variance conditionnelle de ΔYt, définie comme suit :

où V(ΔYt ∣ Ωt-1) = w′D(0) ψD(0)′ w + w′ ∑w. Cette mesure de persistance peut être décomposée en une composante attribuable aux chocs macroéconomiques explicitement identifiés, PS, et l’autre aux « autres chocs » de type sectoriel, PO, soit :

où

Dans le cas univarié où les sources des chocs ne sont pas explicitement identifiés, on peut écrire ΔYt = α + a(L) υt, où α est un scalaire, a(L) est un polynôme de l’opérateur de retards et υt sont des chocs de moyenne nulle, non corrrélés avec une variance commune σ2u. Dans le cas présent, (4) devient equation: 011394are009n.png soit la mesure de persistance popularisée par Campbell et Mankiw (1987).

2. Identification des chocs au niveau de la production agrégée

En divisant la période 1870-1996 en deux sous-périodes, afin de mesurer la persistance des chocs, il est possible d’analyser si la nature des fluctuations de court terme de la production a changé à travers le temps. Les sous-périodes choisies pour les fins de comparaison sont 1870-1914 et 1947-1996; elles sont respectivement désignées comme les périodes d’avant-guerre et d’après-guerre. Ces périodes ont été sélectionnées pour plusieurs raisons. En premier lieu, les séries d’avant-guerre ne débutent qu’en 1870, la première année pour laquelle les séries du PIB par industrie sont disponibles au Canada. En second lieu, les deux guerres mondiales et les dépressions immédiates qui leur ont succédées sont exclues car il est fort vraisemblable que l’expansion due aux deux guerres et la démobilisation subséquente ne fournissent pas d’indication intéressante sur la nature des fluctuations de court terme de l’économie canadienne.

Les nouvelles estimations d’Urquhart (1993) ont confirmé que la croissance économique du Canada a été particulièrement vigoureuse durant le 19e siècle. Cette croissance s’est accélérée à la fin des années 1890 suite à une augmentation exogène dans la demande de blé canadien (voir Urquhart 1986, 1988), connue sous le nom de « boom du blé ». En effet, la croissance économique enregistrée par l’économie canadienne durant la décennie 1900-1910 associée au boom du blé a été l’une des plus remarquable dans l’histoire économique canadienne (le taux de croissance annuel moyen a été de l’ordre de 6 %) et la part de l’investissement brut nominal dans le PNB en dollars courants a alors atteint un record historique (entre 15 et 30 %).

Durant la période après la Deuxième Guerre mondiale, la baisse dans l’activité gouvernementale a été compensée par l’émergence du secteur privé. La relative transition douce de la guerre à la paix durant la fin des années quarante, a inauguré la période de croissance la plus soutenue de l’histoire économique canadienne. La croissance de la population et le ratio de l’investissement au PNB a retrouvé son niveau d’avant la seconde guerre mondiale. Durant la période d’après-guerre, le PNB et la productivité ont connu un taux de croissance remarquable pendant quatre décennies successives pour ne ralentir qu’après le choc pétrolier de 1973. Durant cette même période, le taux d’inflation et de chômage ont commencé à croître.

En résumé, quand on fait exception de la période de l’entre-deux-guerres, la croissance de l’économie canadienne semble avoir été altérée par les deux chocs exogènes retenus : le « boom du blé », dans la période d’avant-guerre et le choc pétrolier de 1973 dans la période d’après-guerre. L’étape suivante consistera à intégrer l’effet de ces deux chocs macroéconomiques dans le modèle multisectoriel, que nous avons retenu, pour analyser le changement dans la persistance des fluctuations de court terme à travers le temps.

3. Spécifications économétriques des chocs

Dans cette section, nous avons utilisé le modèle multisectoriel développé dans la première section pour analyser la croissance de la production de sept secteurs de l’économie canadienne à partir des données historiques annuelles couvrant la période 1870-1996. Ces secteurs représentent la totalité de la production agrégée de l’économie canadienne[2].

La première étape de l’analyse a été d’obtenir un aperçu des propriétés des séries chronologiques de la production sectorielle. Les statistiques de Dickey Fuller augmentées (DFA), pour une variété de retards calculées pour la période considérée, ne permettent pas de rejeter l’hypothèse de racine unitaire pour les séries sur la production sectorielle. Ceci demeure vrai même si l’on permet un changement de tendance occasionné par les chocs macroéconomiques explicitement identifiés (ceci correspond au modèle de changement de croissance à la Perron, 1989). En utilisant la procédure de DFA, nous avons aussi testé et rejeté l’hypothèse de racine unitaire des taux de croissance de la production sectorielle. Ces tests suggèrent qu’il est raisonnable de procéder avec l’hypothèse de stationnarité des séries sectorielles sur la croissance de la production.

De plus, nous avons appliqué la procédure du maximum de vraisemblance de Johansen (1988) pour examiner les propriétés de coïntégration des séries sectorielles de la production et avons trouvé un ou deux vecteurs coïntégrant, dépendamment si l’on utilise les statistiques sur la trace ou les statistiques sur les valeurs propres. Les tests statistiques basés sur la valeur propre maximale de la matrice stochastique suggèrent qu’il y a précisément un vecteur coïntégrant, alors que ceux basés sur la trace de cette matrice suggèrent qu’il en existe deux. Ces résultats sont robustes aux choix de la spécification du modèle. Des résultats similaires ont été obtenu sur la base de modèles VAR d’ordre 2, 3 et 4, avec ou sans tendance dans le processus de génération des données.

Le nombre de vecteurs coïntégrants obtenu, même s’il demeure relativement faible, indique qu’il existe des sources indépendantes de chocs de la production, fournissant ainsi un support empirique à la notion de chocs spécifiques au secteur dans la génération des fluctuations cycliques.

Les résultats sur les statistiques de DFA présentés, ci-dessus, indiquent que le modèle multisectoriel décrit en (1) est un cadre approprié pour examiner la persistance des chocs de l’économie canadienne. Comme exercice préliminaire à l’obtention des estimations des mesures de persistance, nous avons cependant considéré une version simplifiée de (1) où les chocs macroéconomiques ne sont pas explicitement identifiés. Les mesures de persistance sont données par (5) en posant λ = 0 et en interprétant P0 comme la mesure globale de persistance. Dans l’analyse empirique, nous considérons les versions suivantes de (1) :

M1 :

 equation: 011394are010n.png

M2 :

 equation: 011394are011n.png

M3 :

une version restreinte de M2, où les variables avec des coefficients dont la valeur des statistiques t est inférieure à l’unité (en valeur absolue) sont exclues du modèle,

M4 :

 equation: 011394are012n.png

M1 est un modèle VAR non restreint. Il explique la croissance de la production du secteur i, Δyit, en termes de la production retardée de tous les secteurs incluant le secteur i. M2 impose rm × (m – 2) restrictions sur M1 et explique Δyit en termes de croissance de la production retardée du secteur i et les retards sur la croissance de la production agrégée du reste de l’économie (notée par equation: 011394are013n.png). Le modèle M3 impose davantage de restrictions sur M2 pour exclure les variables non significatives et M4 représente le modèle le plus simple dans lequel le logarithme de la production de chaque secteur est caractérisé par une marche aléatoire avec dérive.

Les quatre modèles ont été estimé pour les sept secteurs de l’économie canadienne en incluant jusqu’à cinq retards dans la croissance de la production sectorielle et agrégée en utilisant la méthode du maximum de vraisemblance à information complète (MVIC) pour les périodes 1870-1914 et 1947-1996. Avec m = 7 et r = 5, le modèle M1 est clairement surparamétrisé (252 paramètres), il n’est retenu que comme point de repère. L’imposition de 175 restrictions associées au modèle M2 réduit le nombre de paramètres à estimer à 77. La statistique du ratio de vraisemblance pour le test de ces restrictions est égale à 116,4 (176), ce qui est bien en deçà de la valeur critique à 95 % fournie entre parenthèses, suggérant ainsi la pertinence du modèle. L’imposition de 30 restrictions supplémentaires sur le modèle M2, en annulant les paramètres dont les statistiques t sont inférieures à l’unité en valeur absolue, fait qu’on ne peut pas rejeter ce modèle; la statistique du ratio de vraisemblance pour ce test est 21,5 (43,77). Par contre, le modèle M4 est résolument rejeté en faveur du modèle M3, en raison de la valeur du ratio de vraisemblance égal à 101,8 (55,76).

Les estimations des mesures de persistance sectorielles et agrégées basées sur les modèles M1, M2 et M3 sont fournies dans le tableau 1. Comme il fallait s’y attendre, les mesures de la persistance basées sur les modèles parcimonieux M2 et M3 sont plus précises que celles basées sur le modèle non restreint M1. La mesure de la persistance agrégée obtenue à partir du modèle M3 est estimée à 1,09 durant la période d’après-guerre, en légère hausse par rapport à l’avant-guerre où elle a affiché 1,07. Cette mesure est plus précise que celle des modèle M1 et M2, comme en témoigne l’écart-type fourni entre parenthèses.

Il est intéressant de comparer les résultats obtenus en utilisant des modèles multisectoriels M1 – M3 avec ceux obtenus à partir d’un modèle univarié. Nous avons donc calculé les mesures de persistance à partir de différents modèles ARMA appliqués à la croissance agrégée de la production durant la même période échantillonnale. La spécification la plus générale que nous ayons considérée pour la série agrégée est un modèle ARMA (5,4), quoique les valeurs maximisées du log de la fonction de vraisemblance obtenues à partir de ce modèle et pour des processus ARMA d’ordre plus faibles soient proches. Ceci suggère que le processus de la production agrégée peut être adéquatement caractérisé par une marche aléatoire avec dérive (pour laquelle la mesure de persistance est unitaire).

Tableau 1

Mesures de persistance sectorielle et agrégée : l’avant et l’après-guerre

Mesures de persistance sectorielle et agrégée : l’avant et l’après-guerre

Note : Les mesures de persistance sectorielle, Pi sont estimées en utilisant (5) avec λ = 0 et le vecteur ei à la place du vecteur w. Ces résultats ne tiennent pas compte des chocs macroéconomiques explicitement identifiés. La mesure de persistance agrégée Py utilise w. Les chiffres entre parenthèses sont les écart-types asymptotiques dont les dérivées ont été calculées analytiquement. Leurs formules sont présentées dans l’annexe B de PPL (1993 : 82-85).

-> See the list of tables

Nous avons déjà noté que le modèle M4, pour lequel la production de chaque secteur suit une marche aléatoire avec dérive, est rejeté par les données, de sorte que le résultat univarié est cohérent avec les résultats multisectoriels seulement sous des restrictions particulières sur la taille des coefficients ARMA des équations sectorielles et sur les corrélations entre les chocs sectoriels. Toutefois, il n y a pas de raisons a priori quant à la validité de ces restrictions d’agrégation. Par conséquent, ces résultats soulèvent la question d’un biais d’agrégation pour les modèles estimés au niveau de l’ensemble de l’économie, suggérant ainsi davantage de précautions.

Nous allons, à présent, nous concentrer sur la principale préoccupation de cette étude, qui est d’identifier la contribution des différents types de chocs à la mesure de persistance globale.

Pour répondre à cette question, nous avons considéré la version suivante du modèle multisectoriel complet (1) :

Ce modèle renferme jusqu’à cinq retards dans les taux de croissance de la production sectorielle et agrégée, ainsi que la valeur courante et cinq retards dans les chocs macroéconomiques explicitement identifiés. Le modèle equation: 011394are016n.png doit être complété avec des équations des p types de chocs macroéconomiques, υjt(j = 1, 2, ..., p). Nous considérons deux types de chocs, à savoir : le choc du blé de 1896 pour l’avant-guerre (1870-1914) et le choc pétrolier de 1973 pour la période d’après-guerre (1947-1996).

Les spécifications de chacune des deux équations macroéconomiques utilisées pour déterminer chacun de ces deux chocs macroéconomiques sont présentées dans le tableau 2. Pour chacune des deux équations macroéconomiques (production de blé et prix du pétrole brut), nous avons considéré la variable dépendante avec cinq retards (r = 5). Cependant, pour la spécification de l’équation associée au choc du blé nous avons ajouté deux retards dans le prix de la production et quatre retards dans les dépenses d’investissements privés afin de prendre en compte les phénomènes susceptibles d’expliquer le choc du blé.

Les résultats présentés dans le tableau 2 ont été estimés par la méthode des moindres carrés ordinaires et suggèrent que si le comportement du prix du pétrole peut être adéquatement expliqué par un modèle de type AR, celui de la production du blé requiert le rajout des variables retardées du prix de la production et de l’investissement. En effet, la spécification des équations a été obtenue en ne tenant pas compte de tous les coefficients qui ont un t statistique inférieur à 1,5 en valeur absolue, mais aussi en s’assurant qu’aucune des variables exclues ne soit conjointement significative. De plus, dans la mesure où les résidus estimés de chacune de ces deux équations seront utilisés à titre d’erreur d’anticipation, il est important qu’elles ne renferment pas d’élément systématique.

Ayant établi la forme des équations macroéconomiques à être utilisées pour identifier les chocs macroéconomiques, le système d’équations equation: 011394are017n.png – sept équations expliquant la croissance sectorielle de la production et deux équations identifiant les différents chocs macroéconomiques – a été estimé de façon conjointe en faisant appel à la méthode du MVIC. Nous testons les deux hypothèses nulles suivantes en nous basant sur les statistiques de Wald :

Tableau 2

Estimés des équations utilisées dans la détermination des chocs macroéconomiques

Estimés des équations utilisées dans la détermination des chocs macroéconomiques

Note : Les deux équations ont été estimées par la méthode des moindres carrés ordinaires et les statistiques t figurent entre parenthèses. La variable DLB représente les changements dans le (log) de la production physique du blé; DLPB représente les changements dans le logarithme du prix du blé; DLPP représente les changements dans le logarithme du prix du pétrole; DLI représente les changements dans le logarithme des dépenses d’investissement; le chiffre entre parenthèses indique le nombre de retards de la variable en question; SC représente la statistique du multiplicateur de Lagrange pour tester la corrélation sérielle des résidus (χ2(5)).

-> See the list of tables

Sous H1, les chocs macroéconomiques explicitement identifiés n’ont aucun effet sur la croissance (de court et de long terme) de la production sectorielle; en revanche, sous H2, ces chocs macroéconomiques peuvent avoir des effets de court terme, mais pas d’effets à long terme sur la croissance de la production. En termes clairs, si on ne peut rejeter H1, on ne pourra rejeter H2 car H1 implique H2, mais pas vice versa. Notons que le rejet de H1 et le non-rejet de H2 signifie que les chocs ont des effets à court terme mais n’ont pas d’effets à long terme. Par contre, le rejet des deux hypothèses nulles H1 et H2 indique que les chocs ont des effets à court terme et à long terme.

Les hypothèses H1 et H2 sont rejetées (présence d’un effet à court terme et à long terme) dans tous les cas lors de la période d’avant-guerre, comparativement à cinq fois sur sept pour la période d’après-guerre (les exceptions pour lesquelles on ne peut rejeter H2 sont le transport et le reste de l’économie qui semblent avoir eu des effets seulement à court terme). Ceci suggère qu’en termes d’effets macroéconomiques de long terme sur les différents secteurs de l’économie canadienne, les effets du choc du blé aient été encore plus importants que ceux du choc pétrolier. Alors que le choc du blé a eu un impact de long terme sur la production de tous les secteurs, le choc pétrolier, a eu des effets à long terme sur cinq secteurs et des effets à court terme sur les secteurs du transport et le reste de l’économie.

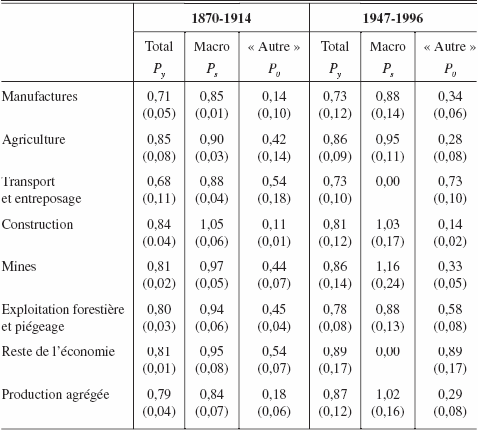
En imposant la restriction H1 là où elle n’a pas été rejetée et en excluant les variables dont la statistique t est inférieure à 1,5, on obtient un nouveau modèle contraint equation: 011394are021n.png à partir duquel on a estimé les mesures de persistance du tableau 3. Les estimations de la persistance sectorielle et agrégée, obtenus avec la méthode MVIC, sont fournies dans la première et la quatrième colonne du tableau 3, respectivement, pour les périodes d’avant et d’après-guerre. Ces dernières ont été à leur tour décomposées en la contribution de la persistance due au choc macroéconomique explicitement identifié et celle due aux chocs « autres ».

Que ce soit au niveau sectoriel ou au niveau agrégé, les estimations de la persistance globale figurant dans le tableau 3 sont non seulement inférieures à celles figurant dans les deux dernières colonnes du tableau 1 mais elles sont encore plus précises comme en témoigne leur écart-type plus faible. Au niveau de la production agrégée d’avant-guerre, la persistance du choc du blé est estimée à 0,84 avec un écart-type (asymptotique) de 0,07. Les effets de la persistance du choc de blé sur la production agrégée sont, à la fois, statistiquement significatifs, sujets à relativement peu d’incertitude et contribuent pour plus des trois quarts à la mesure de la persistance agrégée. Ceci est vrai non seulement au niveau agrégé mais aussi au niveau de chacun des secteurs pour lesquels les hypothèses H1 et H2 ont été résolument rejetées (voir les équations (5) pour la façon de déterminer la contribution des divers types de chocs).

Pour la période d’après-guerre, la contribution du choc macroéconomique explicitement identifié (en l’occurrence le choc pétrolier) à la mesure de persistance globale est nulle pour les secteurs du transport et du reste de l’économie (voir les équations (5) pour la façon de déterminer la contribution λ du choc macroéconomique explicitement identifié). Il s’ensuit que les estimés de la persistance globale, Py, et ceux de la persistance due aux chocs « autres », Po sont identiques. Sur la base des estimés du λ, la contribution du choc pétrolier à la mesure de la persistance globale a été de 60 % dans les secteurs manufacturier, de la construction et de l’exploitation forestière, pêche et piégeage. La contribution a été, respectivement, de 80 % et 50 % dans les secteurs de l’agriculture et des mines. Les résultats des tests de coïntégration ont aussi indiqué que durant l’après-guerre le nombre de sources indépendantes de chocs a été modérément important. Ceci suggère qu’au Canada les chocs spécifiques aux secteurs ont aussi conduit aux fluctuations persistantes dans la production, mais à un degré moindre que le choc macroéconomique identifié. Ces résultats se rapprochent de ceux obtenus par PPL (1993) pour les États-Unis où une fraction importante de la persistance globale des chocs est attribuable aux chocs « autres ».

Tableau 3

Décomposition de la mesure de persistance sectorielle et agrégée par type de chocs : l’avant-guerre et l’après-guerre

Décomposition de la mesure de persistance sectorielle et agrégée par type de chocs : l’avant-guerre et l’après-guerre

Note : Les estimés ont été obtenus en utilisant la méthode MVIC en se basant sur le modèle equation: 011394are023n.png sur lequel a été imposée l’hypothèse H1 et où les variables avec des statistiques t inférieures à 1,5 ont été éliminées. Le nombre de paramètres estimés est de 75 pour la période 1870-1914 et de 71 pour la période 1947-1996.

-> See the list of tables

Les résultats révèlent aussi que dans la période d’après-guerre, la persistance associée au choc pétrolier a contribué pour une part substantielle (plus de 70 %) de la mesure de la persistance de la production agrégée canadienne. Au niveau agrégé, l’estimation de la persistance du choc pétrolier est égale à 1,02 avec un écart-type (asymptotique) de 0,16. Les effets de la persistance du choc pétrolier sur la production agrégée sont, à la fois, statistiquement significatifs mais sujets à beaucoup d’incertitude. Un tel résultat pourrait être expliqué par le fait que nous n’avons considéré qu’un seul choc macroéconomique explicitement identifié, soit celui qui nous a semblé avoir eu un impact certain sur les productions sectorielles.

D’une période à l’autre, les estimations sectorielles, qui étaient élevées, ont enregistré une très légère augmentation. La médiane des productions sectorielles est passée de 0,80 à 0,81 entre l’avant et l’après-guerre. Les secteurs qui ont connu l’augmentation la plus élevée sont les mines, le transport mais surtout le reste de l’économie. Compte tenu du poids que représente le reste de l’économie dans l’après-guerre, soit 58 % en 1996, la persistance de la production agrégée a augmenté tout autant, soit environ 0,08. Notons que les secteurs de la construction et de l’exploitation forestière, pêche et piégeage ont quant à eux enregistré une légère baisse de la persistance. Ces résultats suggèrent que pour la plupart des secteurs, les effets des chocs ont eu tendance à devenir légèrement plus persistants à travers le temps.

Conclusion

Cet article utilise un modèle multisectoriel permettant de mesurer le niveau et le changement de la persistance entre l’avant et l’après-guerre. Les résultats fournissent une justification supplémentaire pour l’usage de l’approche désagrégée non seulement dans l’analyse de la persistance des chocs de la production au niveau sectoriel, mais aussi au niveau de la persistance agrégée. Tout comme dans le cas des résultats obtenus par PPL (1993) pour les États-Unis, les estimations de la mesure agrégée obtenus pour le Canada basés sur un modèle multisectoriel sont plus faibles que celles obtenues au moyen d’un modèle univarié. Du coup, ceci soulève la question de savoir s’il n’existe pas un biais d’agrégation associé au modèle agrégé.

L’utilisation de l’analyse sectorielle nous a permis de constater des résultats différents selon qu’on identifie explicitement les chocs macroéconomiques (tableau 3) ou que l’on amalgame tous les chocs qui affectent les productions sectorielles (version simplifiée présentée dans le tableau 1). En effet, la mesure de persistance de la production agrégée et des productions sectorielles est plus précise. Cependant, bien que la mesure de la persistance des chocs de la production agrégée basée sur le modèle multisectoriel général soit inférieure à celle obtenue à partir du modèle simplifié, il n’en demeure pas moins que la mesure est largement supérieure à zéro, de sorte que la production apparaît en définitive avoir été affectée de façon permanente par les chocs.

Les résultats suggèrent aussi que l’analyse sectorielle est en soi une approche très intéressante car elle permet de mesurer l’impact des chocs sur les différents secteurs, autrement inobservables avec une approche agrégée. Les chocs macroéconomiques identifiés explicitement dans l’analyse ont eu des effets de nature différente. En effet, le « boom du blé » a eu des effets à court et à long terme sur tous les secteurs de l’économie. En revanche, le choc pétrolier a eu des effets à court et long terme sur les secteurs agricole, manufacturier, de la construction, des mines et des forêts, chasse et pêches. Par contre, il n’a eu qu’un effet de court terme sur le secteur du transport et sur celui du reste de l’économie dans l’après-guerre.

Par ailleurs, certains types de chocs ont été plus importants dans certains secteurs que dans d’autres. En effet, le choc du blé a affecté le secteur de l’agriculture de façon substantiellement plus importante que les autres secteurs. Ce choc, qui est spécifique au secteur agricole, a pu avoir de rapides effets de débordements sur des secteurs tels les manufactures, les mines, la construction, les forêts, chasse et pêches, et le reste de l’économie. Le secteur du transport apparaît, selon nos résultats, avoir été affecté par le boom du blé de façon modérée et moindre que les autres secteurs; d’autres facteurs ont pu avoir contribué à la mesure de persistance globale de ce secteur.

Ainsi, les résultats obtenus dans l’avant-guerre indiquent que le boom du blé a largement contribué à l’impact permanent sur la production agrégée et sur les différentes productions sectorielles. Comparativement à la période d’avant-guerre, les résultats obtenus pour l’après-guerre suggèrent que les chocs « autres » ont eu davantage d’impact permanent sur ces mêmes productions sectorielles (en raison des services et du transport). Toutefois, il convient de noter que le choc pétrolier a contribué pour plus de la moitié à la persistance globale de cinq secteurs.

Les résultats obtenus pour la période d’avant-guerre nous permettent de faire le lien avec la théorie du développement historique du Canada. Deux théories quant à l’interprétation du développement économique canadien existent dans la littérature : la théorie traditionaliste et la théorie révisionniste. La théorie traditionaliste, qui remonte au début des années vingt (Mackintosh, 1964), prétend que le secteur des exportations a été la source essentielle de la croissance économique et que le secteur manufacturier n’aurait connu un véritable essor qu’à partir du boom du blé (1896). La théorie révisionniste, plus récente, associée à des auteurs comme Chambers et Gordon (1966), prétend que la croissance du revenu per capita durant la période 1870-1926 n’a pas été attribuable à la présence ou à l’absence de marchés d’exportation.

Les résultats obtenus dans ce papier permettent d’apporter un éclairage additionnel sur la contribution du choc du blé aux persistances globales agrégée et sectorielle et ainsi corroborer la thèse traditionaliste du développement historique du Canada. En effet, comme le montre le tableau 4, avec une contribution de 0,88 à la mesure de la persistance globale agrégée, le choc du blé semble avoir engendré une déviation permanente sur le niveau de la production de l’économie en général; la contribution des chocs « autres » a été relativement modeste. Ceci demeure vrai non seulement au niveau de l’économie dans son ensemble mais aussi au niveau de la plupart des secteurs.

Tableau 4

Contribution du choc macroéconomique explicitement identifié à la mesure de la persistance globale agrégée et sectorielle

Contribution du choc macroéconomique explicitement identifié à la mesure de la persistance globale agrégée et sectorielle

-> See the list of tables

Avec une contribution de 0,86, le secteur agricole est celui où le choc du blé a contribué substantiellement à la persistance globale de ce secteur; en revanche, avec environ 0,60, la contribution de ce choc à la persistance globale des autres secteurs a été relativement plus modeste. Ceci nous suggère que l’origine du choc du blé ait été d’abord sectorielle et, qu’en raison du poids et de l’importance de l’agriculture dans l’économie canadienne entre 1870-1914, ses effets ont débordé sur les autres secteurs.