Le réalisme avec degrés de certitude

Résumé

Dans le contexte de l’utilisation des degrés de certitude avec des QCM (questions à choix multiples), l’évaluateur désire mesurer l’adéquation entre la façon dont les personnes évaluées (souvent les étudiants) utilisent les degrés de certitude et les instructions fournies pour les utiliser. Cette mesure est appelée « réalisme du sujet ». Actuellement, le calcul du réalisme, quoiqu’élémentaire, présente quelques inconvénients de types calculatoire, conceptuel ou probabiliste. Une nouvelle approche de type probabiliste correspondant mieux à la définition des degrés de certitude et à la façon avec laquelle les étudiants doivent les utiliser est décrite ici. Cette approche aboutira à de nouvelles définitions et méthodes de calcul du réalisme basées sur des arguments statistiquement justifiés. Cette nouvelle définition est plus précise que la précédente, et décrit mieux la capacité de s’autoévaluer et d’utiliser correctement les degrés de certitude. Enfin, elle permettra d’améliorer la fiabilité des indices de qualité liés aux questions utilisant le réalisme, par exemple le rpbisSCT de Gilles (2002).

Mots-clés :

• degrés de certitude,
• difficulté,
• docimologie,
• édumétrie,
• QCM,
• réalisme,
• subjectivité,
• probabilité

Abstract

By using confidence marking (CM) along with multiple-choice questions, an examiner needs to measure the consistency and adequacy of CM usage with the instructions given to the student. This measure is called the “realism of the subject”. Although it is easy to compute, the current realism formula entails some conceptual, probabilistic and computational weaknesses. Relying on probability theory and a set of statistically justified arguments, this paper shows a new approach to calculate realism that has a better match to the definition of CM and to the way examiners ask the students to use it. Moreover, the new realism is more precise with respect to the previous and gives a better indication of the student’s self-evaluation skills and his ability to use CM. Finally, this will improve the reliability of items quality indicators which use realism in their calculations such as Gilles’ rpbisSCT (2002).

Keywords:

• confidence marking,
• certainty-based marking,
• difficulty,
• docimology,
• edumetrics,
• multiple-choice questions,
• realism,
• subjectivity,
• probability

Resumo

No contexto de utilização dos graus de certeza das QEM (questões de escolha múltipla), o avaliador deseja medir a adequação entre o modo como os sujeitos (frequentemente os estudantes) utilizam os graus de certeza e as instruções fornecidas para os utilizar. Esta medida é designada como “realismo do sujeito”. Atualmente, o cálculo do realismo, embora elementar, apresenta alguns inconvenientes do tipo calculatório, concetual e probabilístico. Descreve-se aqui uma nova abordagem de tipo probabilístico, a qual corresponde melhor à definição de graus de certeza e ao modo com o qual os estudantes os devem utilizar. Esta abordagem conduzirá a novas definições e métodos de cálculo do realismo baseados em argumentos estatisticamente justificados. Esta nova definição é mais precisa que a precedente, e descreve melhor a capacidade de se autovaliar e de utilizar corretamente os graus de certeza. Por fim, permitirá melhorar a fiabilidade dos índices de qualidade ligados às questões que utilizam o realismo, por exemplo o rpbisSCT de Gilles (2002).

Palavras chaves:

• graus de certeza,
• dificuldade,
• docimologia,
• edumetria,
• QEM,
• realismo,
• subjetividade,
• probabilidade

Introduction

Traditionnellement, lors d’un test à questions à choix multiples (QCM), le résultat est binaire : la réponse est correcte ou incorrecte. Ainsi, l’information sous-jacente est que soit l’étudiant sait, soit il ne sait pas. Cette situation dichotomique ne correspond souvent pas à la réalité des faits, où l’étudiant se questionne et peut douter de la réponse qu’il compte donner. Grâce à l’utilisation des degrés de certitude (DC), on introduit une nuance dans l’appréciation de la compétence, donnant alors la possibilité à l’étudiant d’exprimer un doute au sujet de ses propres compétences (Gilles, 2002).

Les questions à choix multiples avec degrés de certitude

Cette section permettra au lecteur de se familiariser avec la notion de degré de certitude afin de lui permettre de comprendre les développements liés au réalisme. La notion est tirée intégralement de Prosperi (2012). Le lecteur déjà avisé pourra sans doute porter son attention à la section sur la notion de réalisme.

Le principe de fonctionnement

Lorsque des étudiants doivent répondre aux questions d’une épreuve à QCM, ils peuvent aussi accompagner leurs réponses d’une information en lien avec leur degré de confiance dans la réponse donnée, par exemple un nombre de 0 à 5 indiquant dans quelle mesure ils sont sûrs de la réponse donnée. Chaque chiffre peut correspondre à un intervalle de pourcentage prédéfini qui indique l’estimation de la chance de répondre correctement à la question. Cette échelle de certitude recouvre tout l’espace de chance de 0 % à 100 %. À titre d’exemple, Leclercq, Boxus, de Brogniez, Wuidar et Lambert (1993) ont proposé une échelle allant de 0 à 5 (voir figure 1). Si l’étudiant indique une certitude de 0, cela signifie qu’il estime avoir entre 0 % et 25 % de chance de répondre correctement à la question. Pour le degré de certitude 1, cette chance se trouve entre 25 % et 50 %. Pour le degré de certitude 2, cette chance se trouve entre 50 % et 70 %, etc.

Il est possible de construire un grand nombre d’échelles de certitude. Il en existe avec intervalles symétriques, avec intervalles asymétriques (comme celle donnée en exemple) ou encore avec différents nombres d’intervalles (Leclercq, 1982 ; Leclercq et al., 1993). Ces différences sont principalement méthodologiques, par exemple l’échelle donnée en exemple n’est pas symétrique, mais elle propose plus de finesse dans la moitié entre 50 % et 100 %. Ce choix a été fait, car, empiriquement, les étudiants ont tendance à davantage utiliser cette seconde partie de l’échelle par rapport à la première moitié. Cela est dû principalement au fait que l’évaluation a souvent lieu après une séquence d’enseignement-apprentissage (par ex., après avoir suivi un cours). Ainsi, l’étudiant est censé disposer des connaissances et des compétences nécessaires pour répondre correctement à la question, mais il peut en même temps avoir des doutes au sujet de ses acquis (Gilles, 2002).

Figure 1

Intervalles des degrés de certitude

L’utilisation des degrés de certitude permet aussi de donner une rétroaction à l’étudiant ou parfois de mettre en lumière des situations qui pourraient s’avérer dangereuses si non corrigées. Par exemple, dans le cas où l’étudiant donne une réponse fausse avec un degré de certitude 5 (il est absolument certain d’avoir raison), il faut se questionner sur ses acquis dans le sujet couvert par la question (Gilles, 2002). Un exemple concret et emblématique serait celui d’un étudiant en médecine qui choisit d’administrer à un enfant inconscient, avec un degré de certitude 5, une dose d’adrénaline qui lui serait fatale. Un tel test permet donc de détecter des situations dangereuses qui passeraient autrement inaperçues, car elles seraient noyées dans le résultat global du test. Il permet également de donner un retour à l’étudiant pour l’aider à mieux cibler son travail.

L’échelle des scores

Lors du test, l’étudiant donne pour chaque question un couple (soit une réponse et un degré de certitude). À chacun de ces couples est attribué un score, qui dépend de la justesse de la réponse et du degré de certitude lié. L’attribution a lieu sur la base du tarif suivant :

Tableau 1

Score attribué à un étudiant en fonction de l’exactitude de la réponse et du degré de certitude choisi

Ce tarif a été conçu par Leclercq et al. (1993) pour être conforme avec la théorie des décisions, selon laquelle la seule stratégie possible pour maximiser le score est celle de répondre le plus honnêtement possible. Ainsi, l’étudiant qui veut réussir a tout intérêt à exprimer le plus fidèlement possible quelle est sa chance de répondre correctement à la question.

Cette autoévaluation de ses propres connaissances est une compétence qu’il est possible de développer. Il est d’ailleurs fortement recommandé que l’étudiant puisse s’exercer à ce type d’examen utilisant les degrés de certitude.

La notion de réalisme

Le degré de certitude est une estimation de la chance de répondre correctement à la question. Par exemple, en donnant le degré de certitude 3 à une question, la personne évaluée estime entre 70 % et 85 % sa chance de répondre correctement. Dans le cas idéal, elle est parfaitement capable d’estimer sa chance de réussite. D’un point de vue probabiliste, ceci signifie que l’étudiant devrait avoir entre 70 % et 85 % de réponses correctes parmi toutes celles auxquelles il a donné la certitude 3.

Ce passage à un raisonnement probabiliste découle directement de la définition de DC. Une personne qui est parfaitement capable d’évaluer ses compétences et ses chances de réussite pour chaque DC devrait obtenir un taux d’exactitude dans l’intervalle défini par le DC.

Or, dans la pratique, il existe deux facteurs qui écartent l’étudiant du cas idéal : une mauvaise estimation de ses chances de réussite et la variation aléatoire due au raisonnement probabiliste. Ces deux points seront analysés ci-dessous.

Pour déterminer dans quelle mesure l’étudiant s’écarte du cas idéal, il faut recourir à la notion de réalisme. En 1973, Shuford et Brown (1973) proposent une notion de réalisme représentée par une fonction affine y = ax+b, qui met en relation la probabilité subjective de réussite (les DC utilisés) comme abscisses et le taux effectif de bonnes réponses comme ordonnées. Le cas idéal est une diagonale, y = 1x+0. Plus a et b s’écartent respectivement de 1 et 0, moins l’étudiant sera réaliste. Cette définition donne une vision très fine de l’utilisation que l’étudiant fait des DC sur le plan de la surestimation et de la sous-estimation de ses capacités et de biais subjectif dans l’expression de ses chances de réussite. Cependant, cette définition ne permet pas, ou très peu, de mettre en relation les étudiants les uns avec les autres afin de comparer facilement leur réalisme.

En donnant suite à des travaux de Murphy et d’Oskamp dans les années 1960 et 1970, Leclercq, Jans, Georges et Gilles (2000) proposent une formule qui donne une valeur du réalisme sur une échelle de 0 à 100. Cette définition permet de comparer le réalisme des étudiants les uns par rapport aux autres, et se base sur la différence entre le taux d’exactitude pour chacun des DC et la valeur centrale de l’intervalle de certitude correspondant (voir tableau 2). Enfin, Gilles (2002) propose une adaptation de la formule de Leclercq et ses collaborateurs qui permet de remédier à des aberrations liées aux cas extrêmes d’individus qui utilisent le degré de certitude maximal en se trompant systématiquement ou, au contraire, qui utilisent le degré de certitude maximal en répondant correctement à toutes les questions.

Afin de permettre la compréhension des éléments qui ont motivé ce travail, nous illustrons le fonctionnement de la procédure proposée par Gilles, suivant la formule (1) présentée ci-dessous. Premièrement, nous postulons que les valeurs centrales des intervalles de certitude représentent des taux d’exactitude idéaux pour chaque DC, comme il est précisé dans le tableau 2. Par exemple, pour le DC 1, le taux d’exactitude idéal serait au centre de l’intervalle [0,25 ; 0,5], donc d’une valeur de 0,375. Ainsi, un étudiant j [par la suite, nous utiliserons l’indice j (j=1,...,N) pour indicer des valeurs relatives aux étudiants] réaliste devrait obtenir 37,5 % de bonnes réponses parmi toutes celles qui sont accompagnées du DC 1.

Tableau 2

Valeur centrale des intervalles de certitude et taux idéaux de bonnes réponses

Ensuite, nous calculons, pour chaque DC, l’écart arithmétique en valeur absolue entre le taux effectif de bonnes réponses et le taux idéal. Enfin, tous ces écarts sont sommés, en étant préalablement pondérés par la proportion d’utilisation de chaque DC.

Cette somme représente l’erreur d’utilisation des DC de l’étudiant j et est appelée moyenne des erreurs de certitude (MEC_j). Elle est soustraite de la valeur 1 afin de donner un taux de réalisme facile à interpréter par l’utilisateur : plus il est proche de 1, plus le participant est réaliste. Dans le calcul, Gilles (2002) ajoute deux facteurs de correction, α = 100/95 = 20/19 ≈ 1,0526 et β = 0,025, dont l’utilité est décrite ci-dessous.

Un participant qui n’utilise que le DC 5 et qui se trompe à toutes les questions aura une MEC_j de 0,975 et, donc, un réalisme de 0,025. Cependant, pour relever ce cas limite, nous préférons reporter cette valeur à 0 en soustrayant b dans le calcul du réalisme.

D’autre part, un participant qui encore une fois n’utilise que le DC 5, mais qui cette fois répond toujours correctement aura une MEC_j de 0,025 et un réalisme de 0,95 après la correction β. Nous multiplions la valeur du réalisme par a pour ramener le réalisme de ce cas particulier à 1.

La formule utilisée pour le calcul du réalisme du sujet (Rs_j) est la suivante:

équation (1)

où:

i	= l’indice des degrés de certitude, nc=5
VCi	= la valeur centrale de la certitude i (en pourcentage)
NCi,j	= le nombre de réponses correctes pour la certitude i
NUi,j	= le nombre d’utilisations de la certitude i (si NUi,j = 0, l’indice i est ignoré)
TEi,j	= le taux d’exactitude de la certitude i (en pourcentage) = 100 x NCi,j/NUi,j
NR	= le nombre total de réponses au test.

Cette approche a l’avantage d’être d’une formulation simple et directement calculable, même par le participant lui-même. Cependant, elle présente quelques inconvénients de types calculatoire, conceptuel et probabiliste.

Le premier inconvénient est soulevé par Gilles (2002) et réside dans le fait que le calcul permet d’atteindre des valeurs plus grandes que 1. Ceci est dû au fait qu’il existe des situations où l’erreur minimale est 0. Par exemple, dans le cas d’un étudiant j qui utilise uniquement le DC 2 lors d’un test de 10 questions auquel il donne 6 réponses exactes, la valeur centrale du DC est 0,6, ce qui correspond dans ce cas au taux d’exactitude.

Ainsi, le réalisme est calculé par Rs_j = ((1-(0,6-0,6)·10/10)-0,025)·20/19 = ((1-0)-0,025)·20/19 = (1-0,025)·20/19 = 0,975·20/19 = 1,0263...

Cette aberration provient d’un compromis qui permet d’attribuer la valeur Rs_j = 0 à un étudiant qui se trouve dans une situation de méconnaissance totale, c’est-à-dire qui se trompe systématiquement en utilisant uniquement le DC 5.

Un deuxième inconvénient de la formule (1) est qu’elle ne fait référence qu’à la valeur centrale de l’intervalle de certitude de chaque DC. Cependant, par définition, un DC consiste en un intervalle de probabilité de répondre correctement à une question. Par exemple, un participant choisit le DC 1 s’il estime avoir entre 25 % et 50 % de chance de répondre correctement à une question.

Ainsi, le fait de considérer uniquement la valeur centrale comme la « moyenne du taux d’exactitude » est une trop grande simplification de la signification de DC. Par exemple, un étudiant j qui utilise uniquement le DC 0 et qui a un taux d’exactitude TE_0,j = 24,9 % aura, selon la formule (1) et avec VC₀ = 0,125, un réalisme de (1-(0,249-0,125)-0,025)·20/19 = (1-0,124-0,025)·20/19 = 0,851·20/19 = 0,895.

Afin d’assurer une cohérence avec la définition des degrés de certitude, il faut considérer qu’un étudiant a utilisé correctement le DC i si son taux d’exactitude pour les questions portant sur le DC i (noté TE_i,j) est inclus dans l’intervalle de certitude défini pour chaque DC i. Le réalisme de ce participant a donc subi une réduction non justifiée de 0,105, quand, en réalité, son comportement est parfaitement conforme à la définition des degrés de certitude.

Le niveau de confiance de TE_i,j

Un dernier inconvénient de la formule (1) est qu’elle fait uniquement référence au rapport TE_i,j sans considérer le niveau de confiance d’un tel rapport. En d’autres termes, la question de savoir si le taux d’exactitude est vraisemblable n’est pas posée. Par exemple, un taux d’exactitude TE_i,j = 0,625 peut provenir d’un rapport de 5 questions correctes sur 8 ou de 20 sur 32 : TE_i,j = 5/8 = 20/32 = 0,625. Dans le cas du 20/32, le taux d’exactitude réel de l’étudiant sera très vraisemblablement proche de 0,625. Par contre, dans le cas de seulement 8 observations de l’utilisation du DC i, il est possible que ce taux ait subi une fluctuation due à l’échantillonnage avec un petit nombre de cas.

Nous introduisons donc un nouveau point de vue de type probabiliste afin de déterminer un intervalle de confiance autour du rapport TE_i,j qui permet d’encadrer le vrai taux d’exactitude avec un niveau de confiance donné et de s’affranchir en même temps de la valeur TE_i,j. Brièvement, pour un étudiant j, le nombre de réponses correctes parmi toutes les questions portant le DC i (noté NC_i,j) peut être interprété comme étant la réalisation d’une variable aléatoire suivant une loi binomiale B(n_i,j,p_i,j) avec un paramètre n_i,j = NU_i,j (le nombre d’utilisations du DC i) et un autre paramètre p_i,j inconnu. Un intervalle de confiance pour ce paramètre p_i,j peut être calculé avec la méthode de Wilson (seuil de 90 % ; Newcombe, 1998) à partir de NC_i,j. Cet intervalle noté [a_i,j,b_i,j] contient TE_i,j.

À l’aide de cet intervalle, une notion probabiliste de réalisme peut être introduite avec la définition suivante :

Définition 1. Un participant j utilisant les DC lors d’un test est dit réaliste pour le DC i, avec i dans {0,1,...,5}, si l’intervalle de confiance [a_i,j,b_i,j] a une intersection non vide avec l’intervalle de certitude du DC i.

Le réalisme probabiliste

Cette section présente une nouvelle façon de calculer le réalisme du sujet qui permet de résoudre les trois inconvénients mis en lumière dans les sections précédentes quant à la formule (1).

L’idée à la base du réalisme est celle d’un indicateur qui, a priori, a une valeur de 100 % et qui décroît proportionnellement à une mesure relative aux réponses d’un étudiant et à son utilisation des DC (par ex., la MEC_j). Ici, nous appellerons cette mesure « l’erreur d’estimation totale ». Nous calculons d’abord l’erreur d’estimation pour chaque DC i. Celle-ci aura une valeur de 0 si et seulement si l’étudiant est réaliste pour le DC pris en considération:

Définition 2. L’erreur d’estimation pour l’étudiant j et le DC i, notée err_i,j, est donnée par:

• err_i,j = 0 si l’étudiant est réaliste pour le DC i.

• Sinon, err_i,j ≠ 0 et l’étudiant n’est pas réaliste pour le DC i. De plus, on note par [c_i, d_i] l’intervalle de certitude défini par le DC i et on définit:

  • Si b_i,j < c_i, alors err_i,j = c_i- b_i,j,

  • sinon err_i,j = a_i,j –d_i.

Figure 2

Schématisation du calcul de l’erreur d’estimation

En d’autres termes, on calcule une erreur d’estimation si et seulement si l’intervalle de confiance [a_i,j,b_i,j] a une intersection vide avec l’intervalle de certitude du DC i. Une interprétation graphique est donnée à la figure 2.

Une fois que toutes les erreurs d’estimation ont été calculées, l’erreur d’estimation totale peut être calculée, notée simplement err_j, comme somme des err_i,j pondérées par NU_i,j/NR.

Définition 3. L’erreur d’estimation totale, notée err_j, vaut :

où NU_i,j est le nombre d’utilisations du DC i et où NR = Ʃ⁵₀NU_i,j est le nombre total de questions du test.

Par construction, la valeur maximale que peut atteindre err_j est 0,95 (avec NR et une utilisation du DC 5 partout). Pour calculer le réalisme, err_j sera soustraite de la valeur 0,95 (et pas de 1). Enfin, pour obtenir une valeur en pourcentage, nous divisons par 0,95.

À des fins de comparaison, ce « nouveau réalisme » sera noté Rsn, tandis que Rs sera conservé pour celui décrit dans la section sur la notion de réalisme.

Définition 4. Le réalisme de l’étudiant, noté Rsn_j, est donné par :

La comparaison entre Rs et Rsn

Afin de comparer les deux formules du réalisme, nous observons les résultats du test de maîtrise du français organisé en Belgique par le Groupe Évaluation du français pour l’enseignement supérieur (EFES) pour l’année 2009 sur un échantillon de 3308 participants. Les participants sont de futurs enseignants d’école supérieure agissant en milieu francophone et le test est composé de 60 questions à choix multiples avec DC.

L’analyse descriptive

L’observation la plus directe de la différence entre les deux indices de réalisme est donnée graphiquement par leur distribution (voir figure 3). La distribution de Rsn n’est plus en cloche, mais est très asymétrique. Ce comportement est habituel pour des données qui présentent une valeur maximale, dans ce cas 1. La première observation est que la nouvelle définition du réalisme utilise la valeur maximale plus souvent que Rs. Ceci signifie que Rsn départage en premier lieu les individus réalistes des moins réalistes.

Figure 3

Comparaison des distributions de Rs et Rsn

L’utilisation plus concrète de la valeur 1 par rapport à Rs (504 étudiants ont une valeur de Rsn = 1) permet à l’étudiant de savoir s’il a correctement utilisé les DC par rapport à son autoévaluation. D’autre part, elle indique aussi à un étudiant qui n’a pas obtenu la valeur 1 qu’il lui est possible de s’améliorer.

Les données descriptives pour Rs et Rsn sont présentées dans le tableau 3. La moyenne de Rsn, 0,9417, est considérablement plus grande que celle de Rs, 0,7783.

Tableau 3

Données descriptives de Rs et Rsn

Les corrélations et les régressions

Des études relativement récentes (Moore & Healy, 2008 ; Stankov, Lee, Luo, & Hogan, 2012) suggèrent qu’il n’est pas possible a priori de dissocier le réalisme d’un étudiant j de son taux d’exactitude global au test (TEG_j), car celui-ci est lié à la difficulté de la tâche. Selon ces auteurs, l’étudiant aura tendance à se sous-estimer lors d’une tâche facile et à se surestimer lors d’une tâche difficile. Un même test peut être perçu comme facile ou difficile selon l’état de connaissance de l’étudiant, et cette différence de perception peut introduire un biais dans l’expression de la chance de réussite à la question. Pour cette raison, la qualité du nouvel indice Rsn ne sera pas étudiée en relation directe avec TEG_j, mais plutôt indirectement, en observant la relation entre le réalisme et le score pondéré au test sur des étudiants ayant un TEG_j semblable. Par construction du couple (DC et échelle des scores), la seule stratégie pour maximiser son score est celle d’être le plus réaliste possible (voir la section sur l’échelle des scores). Ainsi, un indicateur de réalisme devrait agir comme un bon prédicteur du score pondéré pour un niveau de TEG_j donné. La comparaison entre Rs et Rsn à ce niveau montre que Rsn est un meilleur prédicteur du score pondéré que Rs en matière de corrélation et de relation linéaire (plus de linéarité et plus de variance expliquée).

Une première observation de ce phénomène est donnée par le nuage de points de la relation entre le réalisme et le score pondéré (voir figure 4). Ces quatre graphes, choisis à titre d’exemple, montrent cette relation pour les intervalles de taux d’exactitude global (TEG) entre 0,45 et 0,5 et entre 0,55 et 0,6. Le nuage de points pour Rsn semble avoir une allure plus linéaire et présente moins de dispersion.

Figure 4

Nuage de points de Rs et Rsn avec le score pondéré pour deux intervalles de TEG

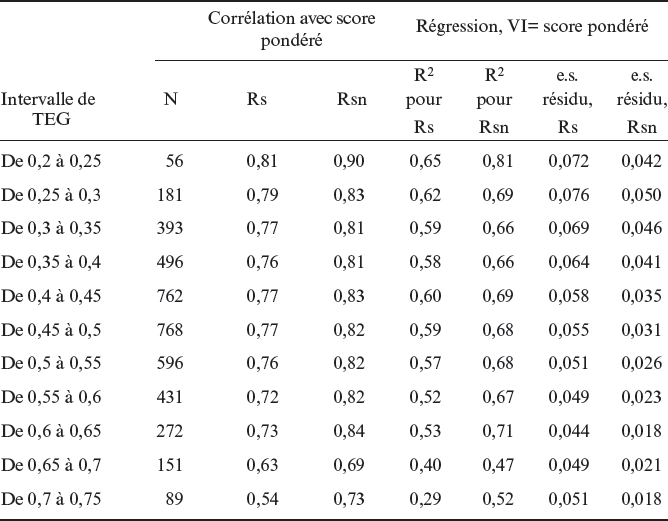
Le tableau 4 montre la corrélation entre le score pondéré avec Rs et Rsn et les données liées à la régression linéaire entre les deux valeurs du réalisme et le score pondéré. Chaque ligne correspond à un groupe d’étudiants avec un TEG semblable (largeur de l’intervalle de 0,05).

Tableau 4

Corrélation et régression de la variable indépendante Score pondéré par les variables dépendantes Rs et Rsn selon le niveau de TEG

La corrélation de Rsn avec le score pondéré est systématiquement plus grande que celle de Rs. De plus, la régression linéaire de Rsn permet d’expliquer plus de variance du score pondéré que celle de Rs (en moyenne 12 % de plus) et a une erreur standard du résidu inférieure. Ainsi, Rsn s’avère être un meilleur prédicteur du score pondéré et est donc plus conforme au message transmis aux étudiants quant à la nécessité d’être réalistes pour maximiser leur score.

La corrélation point bisériale spectrale

La redéfinition du réalisme a un impact sur les instruments d’analyse des questions d’un test qui l’utilisent dans leurs calculs. C’est notamment le cas de la corrélation point bisériale spectrale contrastée avec traitement turbo, appelée rpbisSCT, qui a été introduite par Gilles (2002). Cette corrélation vise à identifier si, pour une question, l’utilisation des DC est cohérente avec l’exactitude des réponses. Par exemple, les étudiants qui ont donné la réponse correcte devraient aussi avoir utilisé un DC plus élevé que les étudiants qui ont donné une réponse incorrecte. Cette situation est appelée cohérence spectrale. Une valeur positive indique que la question respecte ce principe, tandis qu’une valeur négative indique que le postulat n’est pas respecté. Ceci peut avoir lieu lorsque la question est mal formulée ou comporte un piège cognitif.

Afin de donner plus de force à cette valeur de corrélation, seuls les étudiants qui ont un indice de réalisme élevé ont été sélectionnés pour les calculs. Cette opération permet de réduire la perturbation liée à la mauvaise utilisation des DC. Elle est appelée traitement turbo. Pour Rs, on sélectionne traditionnellement les participants avec un taux supérieur à 0,80 ou, pour encore plus de précision, à 0,90. Cette opération peut comporter une réduction substantielle de l’effectif, car les participants ayant un Rs ≥ 0,90 sont plus rares. Par exemple, dans le cas de l’examen de l’EFES de 2009, la sélection des étudiants très réalistes (Rs ≥ 0,90) réduit l’effectif de 3308 à seulement 345. Ceci peut avoir comme effet de réduire la généralité des calculs effectués (Gilles, 2002). Avec Rsn, la sélection des participants réalistes est plus adéquate, ce qui augmente la fiabilité de l’indice rpbisSCT. En effet, par rapport au TEG_j, il peut être démontré que les 504 étudiants sélectionnés avec Rsn = 1 sont distribués d’une façon plus semblable à la distribution de la population totale que la sélection avec Rs ≥ 0,90, qui a tendance à surreprésenter les étudiants avec un TEG_j élevé (Gilles, 2002). La représentativité de l’échantillon avec Rsn = 1 est comparable à celle avec Rs ≥ 0,80, alors que ce dernier est composé de 1481 étudiants sur 3308. Ainsi, avec Rsn = 1, nous obtenons une sélection d’étudiants réalistes dont la composition en matière de TEG_j représente bien la population totale.

La méthode proposée par Gilles introduit un facteur arbitraire qui est celui du choix du pilier Rs ≥ 0,80 ou Rs ≥ 0,90. Avec Rsn, les étudiants réalistes sont ceux qui ont une valeur de Rsn = 1. Cette valeur n’est alors plus arbitraire, mais correspond à l’ensemble des étudiants qui utilisent les DC conformément aux instructions.

Sur l’ensemble des trois tests de l’EFES des années 2009, 2010 et 2011 (n = 9289), la moyenne de 13,6 % d’étudiants avec Rs ≥ 0,90 passe à une moyenne de 19,30 % d’étudiants avec Rsn = 1. La comparaison des indices rpbisSCT pour chacune des trois années montre que l’indice rpbisSCT calculé avec le critère Rsn = 1 (noté par la suite [rpbisSCT(Rsn=1)]) est comparable à l’indice calculé avec le critère Rs ≥ 0,85 [rpbisSCT(Rs ≥ 0,85)], qui utilise en moyenne 32 % des étudiants. Selon Gilles (2002, p. 220-230), la relation [rpbisSCT(Rs ≥ 0,80)] ≤ [rpbisSCT(Rs ≥ 0,90)] est souvent observée. L’observation des trois tests de l’EFES le confirme et, de plus, montre la relation suivante : [rpbisSCT(Rs ≥ 0,80)] ≤ [rpbisSCT (Rsn=1)] ≤ [rpbisSCT(Rs ≥ 0,90)].

Ces observations suggèrent que [rpbisSCT(Rs ≥ 0,80)] est un peu trop pessimiste, car il inclut des étudiants peu réalistes et que [rpbisSCT(Rs ≥ 0,90)] est un peu trop optimiste, car l’échantillon est peu représentatif de la population totale. Quant à [rpbisSCT(Rsn=1)], il reflète mieux la réalité. Cependant, dans ce contexte, l’avantage principal de Rsn par rapport à Rs est celui de la sélection moins restrictive des étudiants, ce qui est particulièrement sensible lors de tests avec un petit effectif, où on veut quand même garder un niveau de précision élevé de l’indice rpbisSCT.

Les vecteurs de réalisme et la surconfiance

Au lieu de calculer un seul indice err_j qui résume en une valeur le réalisme de l’étudiant j, il est possible de présenter le vecteur v_j des erreurs err_i,j : v_j = (err_0,j, err_1,j, err_2,j, err_3,j, err_4,j, err_5,j), où on attribue à err_i,j un signe positif en cas de surconfiance (c’est-à-dire l’étudiant réussit moins bien que ce qu’il annonce) et négatif dans le cas inverse. Cela permettrait à l’étudiant de voir de façon plus précise à quel niveau de certitude l’estimation de ses compétences n’est pas précise. L’observation de l’ensemble des 9289 vecteurs de tous les étudiants des trois tests de l’EFES des années 2009, 2010 et 2011 montre en moyenne de la surconfiance pour les DC de 2 à 5 (c’est-à-dire les tâches pour lesquelles l’étudiant pense avoir plus de 50 % de chance de réussite) et de la sous-confiance pour les DC 0 et 1 (c’est-à-dire les tâches pour lesquelles il pense avoir moins de 50 % de chance de réussite). Ce résultat peut être observé à la figure 5. Une valeur positive indique de la surconfiance, tandis qu’une valeur négative indique de la sous-confiance. Ce graphe est en accord avec les observations reportées par Lemaire (1999). Cet auteur reporte non seulement des observations en accord avec nos données, mais suggère qu’un travail de questionnement de ses propres compétences (par exemple, s’entraîner à utiliser les DC) permet de réduire la surconfiance (et la sous-confiance).

Figure 5

Erreur d’estimation moyenne en fonction du DC

Conclusion

La nouvelle définition du réalisme proposée dans cet article permet de s’affranchir des principaux inconvénients liés à l’approche proposée par Gilles (2002). L’élément le plus important est l’abandon de la référence à la valeur centrale de l’intervalle de certitude introduite dans les années 1960. Ce résultat est démontré par le biais d’une approche probabiliste, notamment par l’utilisation de la méthode de Wilson. Grâce à cette nouvelle méthode de calcul, il est maintenant possible de respecter la consigne sur l’utilisation des DC, soit choisir le DC i si on estime que la chance de réussite se trouve entre c_i et d_i. En effet, la définition précédente, basée sur la valeur centrale de l’intervalle de certitude, sacrifiait la nuance selon laquelle le niveau de certitude peut se trouver à n’importe quel point dans l’intervalle [c_i, d_i].

Cette approche permet de définir un intervalle de confiance pour le taux d’exactitude en considérant le nombre de réponses données avec chaque DC. L’intervalle sera de plus en plus serré avec l’augmentation de ce nombre.

L’indice Rsn est ainsi plus conforme à la réalité, c’est-à-dire qu’il reflète mieux la façon avec laquelle les participants utilisent les DC. En d’autres termes, il mesure mieux le niveau d’adaptation du processus « autoévaluation, choix de la certitude » avec le niveau de certitude « exprimé ».

Cette nouvelle définition aura un impact non seulement sur la rétroaction directe à l’étudiant, mais aussi sur les indices qui intègrent la notion de réalisme pour leur calcul, notamment pour le calcul de l’indice rpbisSCT (Gilles, 2002) et pour la difficulté subjective DS90 (Prosperi, 2012). Ces indices pourront profiter de cette nouvelle définition et son impact devra être évalué. La mise à l’épreuve de Rsn dans ce contexte permettra, sans doute, de confirmer que cette nouvelle méthode de calcul diminue le nombre de faux positifs et de faux négatifs en améliorant la qualité de rétroaction du docimologue.