Abstracts
Abstract
This article explores the scientific and literary work of William Rowan Hamilton (1805-1865). Hamilton was recognised as one of the finest scientists of his generation, and he made lasting contributions to the discipline that eventually became known as ‘physics’. In addition, though, he was fascinated by the relationship between mathematics and poetry. He wrote extensively about this subject, and, from 1827 onwards, he sustained a close friendship with Wordsworth who provided detailed critical analyses of Hamilton’s own poems. Influenced by these revealing exchanges, Hamilton identified poetical qualities in physical and mathematical treatises, and this article probes his views concerning these perceived interconnections with reference to other ‘Romantic’ scientists such as Humphry Davy. In particular, Hamilton’s striking claim that a text such as Joseph-Louis Lagrange’s Mécanique Analytique (1788) can be viewed as ‘a kind of scientific poem’ is assessed.
Article body
I. Introduction
The nature of the relationship between literature and science during the Romantic period is a topic that has provoked lively critical debate for many years now. Numerous studies have sought either to elucidate the many influences that scientific research exerted upon literature, or else to reveal the broader cultural resonances that can be detected within contemporaneous scientific texts, and publications such as Andrew Cunningham and Nicholas Jardine’s Romanticism and the Sciences (1990), Stefano Poggi and Maurizio Bossi’s Romanticism in Science (1994), David Knight’s Science in the Romantic Era (1998), Tim Fulford, Debbie Lee, and Peter Kitson’s Literature, Science and Exploration in the Romantic Era (2004), and Noel Jackson’s Science and Sensation in Romantic Poetry (2008) are only a few of the monographs which explore these sorts of issues. Not surprisingly, such studies have prompted a sustained re-examination of the manner in which both the subjects and methodologies of science and literature changed during the period, and our appreciation of the cultural complexity of this extraordinary epoch has been extensively transformed. However, despite the depth and scope of such reassessments, the main focus has generally been upon the interrelations that associated literary works with ‘life’ and ‘earth’ sciences (such as biology, geology, and chemistry), and comparatively few studies have concentrated specifically upon the interactions between literature and ‘formal’ sciences such as pure mathematics and theoretical (as opposed to experimental) physics. Consequently, partly to redress the balance, the present article probes the perceived connections between mathematics and poetry in the first decades of the nineteenth century, and the main focus falls upon both the literary and scientific work of William Rowan Hamilton (1805-1865). Although Hamilton is still recognised today as one of the most important mathematicians and physicists of his generation, his theories concerning literature and his own poetical compositions have been unjustifiably neglected. This disregard is unfortunate since, throughout his life, Hamilton brooded continually upon the nature of the correspondence between science and literature, and his various pronouncements concerning such matters are often detailed and insightful. In this article, therefore, Hamilton’s scientific and literary writings are assessed, and this discussion seeks not only to illuminate both his friendship with Wordsworth and the cultural significance of his own poetical and mathematical work, but also to examine the curious and elusive connections that he recognised as existing between these two domains. In particular, his remarkable claim that axiomatic-deductive scientific texts can be evaluated as quasi literary compositions is considered in some detail.
II. Your Joint Abode
William Rowan Hamilton was born in Dublin in 1805; he grew up there and subsequently attended Trinity College as an undergraduate, before being appointed, in 1827, both as the Andrews’ Professor of Astronomy in the University of Dublin and as Royal Astronomer of Ireland. This precocious rise ensured that Hamilton came into contact with the finest scientists of the age, and his own achievements secured for him the admiration of his contemporaries.[1] To summarise (all too briefly) just a few aspects of Hamilton’s scientific work, the method of general dynamics that he devised in the 1830s introduced the operator (later called the ‘Hamiltonian’ operator) which eventually provided a key analytical tool for Quantum Mechanics; his sketch of an algebra founded upon the notion of pure time largely anticipated Brouwerian Intuitionism; and his theory of Quarternions, which contributed to the development of non-commutative algebras in his own day, has recently begun to find extensive practical applications.[2] However, despite sustaining an illustrious career as a professional physicist and mathematician, Hamilton repeatedly claimed that he was primarily a poet rather than a scientist. Indeed, so great was his preoccupation with verse that, at various points in the late 1820s and early 1830s, he semi-seriously contemplated renouncing science for literature entirely, and the dilemma that Hamilton encountered during these years was sufficiently complex and revealing to merit closer consideration.
William Wordsworth (1770-1850) had first met Hamilton in 1827, and the two men exchanged letters regularly. In November 1831, Wordsworth received in the post two letters from Hamilton which contained (in total) nine sonnets. Understandably alarmed by this unsolicited profusion of verse, Wordsworth subsequently advised his young friend to devote himself primarily to science, and not to allow himself to be led astray by poetry:[3]
You send me showers of verses which I receive with much pleasure, as do we all; yet have we fears that this employment may seduce you from the path of Science which you seem destined to tread with so much honour to yourself and profit to others. Again and again I must repeat, that the composition of verse is infinitely more of an art than men are prepared to believe, and absolute success in it depends upon innumerable minutiae, which it grieves me you should stoop to acquire a knowledge of.
Graves I, 491
This subtle response clearly expresses dissuasion adroitly ornamented with praise: poetry is presented primarily as a distraction that may cause Hamilton to deviate from “the path of Science” (with the verb “seduce” hinting at the suspect nature of the temptation), while the composition of verse is described as being an “art”[4] that is characterised by a dependency upon countless (unspecified) “innumerable minutiae”. Intriguingly, it is implied that the laborious necessity of mastering such details is beneath the dignity of a man of “Science”, with the consequence that such an undertaking would inevitably require some sort of rather demeaning stooping.
While Wordsworth’s disingenuous advice may in part have reflected his understanding of the differences that distinguish science and poetry, his comments were also no doubt partly prompted both by his personal knowledge of Hamilton and by his tremendous admiration for the latter’s scientific work. When they had first met, in September 1827, Hamilton, who was already recognised as a fine mathematician with a burgeoning international reputation, was on a walking tour in the Lake District.[5] They enjoyed each other’s company and they agreed to correspond. As indicated above, Hamilton’s epistles frequently contained examples of his poetry which he respectfully submitted to Wordsworth for criticism and appraisal. Consequently, the two letters that Wordsworth received in November 1831 were necessarily viewed in the context of this ongoing correspondence, a circumstance which no doubt explains why he expressed concern at the speed and frequency with which Hamilton produced his poetry. For instance, later in his reply, Wordsworth suggested that Hamilton should consider writing prose rather than verse “not because these regions are humbler, but because they may be gracefully and profitably trod with footsteps less careful and in a measure less elaborate” (494). The basic point here is clear: verse requires a more parsimonious and exacting approach, while prose is more amenable to less finely wrought prolixity. This theme reappears in a number of Wordsworth’s letters to Hamilton when he stresses the importance of poetical ‘style’. For instance, he commented in 1829 that “something of a style more terse, and a harmony more accurately balanced must be acquired before the bodily form of your verses will be quite worthy of their living souls” (334); and when he focused on specific examples rather than offering general criticisms of this kind, he often recommended the avoidance of unusual linguistic structures. In particular, one of Hamilton’s poems, ‘To Poetry’, which he had sent to Wordsworth in 1829, begins with the apostrophe “Spirit of Beauty and of tender joying” (316), a line that prompted the following censure:
[...] joying for joy or joyance is not to my taste – indeed I object to such liberties upon principle. We should soon have no language at all if the unscrupulous coinage of the present day were allowed to pass, and become a precedent for the future. One of the first duties of a writer is to ask himself whether his thought, feeling or image cannot be expressed by existing words or phrases, before he goes about creating new terms, even when they are justified by analogies of the language.
351
In his 1989 biography of Wordsworth, Stephen Gill remarked that Wordsworth’s letters to Hamilton deserve to be better known primarily because they offer “practical criticism, with a Johnsonian eye for slackness in diction and image”, and the above extract is a good example of this (Gill 1989, 355). In particular, Wordsworth’s attitude towards neologisms seems to be close to that promulgated by rhetoricians and grammarians such as George Campbell (1719-1796), Hugh Blair (1718-1800), and Lindley Murray (1745-1826) in the late eighteenth century. For instance, influenced by both Campbell and Blair, in the Appendix to his 1795 English Grammar, Murray identifies the property of “purity” which he defines as “the use of such words or constructions as belong to the idiom of the language which we speak, in opposition to words and phrases that are obsolete, or new-coined, or new-modelled, or ungrammatical, or not English” (Murray 1795, 180). This is similar to Wordsworth’s stance, since his objection to “joying” is that it is a gratuitous neologism. Although specifically provoked in this case by an undesirably innovative gerund, Wordsworth seems generally to have believed that Hamilton was insufficiently attentive to the rigours of poetical composition, and he mistrusted this lack of diligence concerning small linguistic details.
Remarkably, therefore, Wordsworth’s advice to Hamilton insinuates a stance that was to become more familiar as the nineteenth century progressed. In essence, science and poetry are presented as being separate disciplines, and time devoted to the mastering of one is time wasted if the individual concerned is better suited to the other. However, caution is required here. In particular, it would be misleading to attribute to Wordsworth an overly simplistic, dichotomistic view of these two domains, since it is well-known that he did not generally consider them to be polarised and entirely distinct.[6] Significantly, Hamilton himself appears broadly to have shared Wordsworth’s assessment of both the “dangers and advantages of science”, since he referred extensively to Wordsworth’s writings on this topic in the lectures on astronomy that he delivered in the 1830s (489), and, despite their complexity, Wordsworth’s views concerning the similarities and differences that relate and separate science and literature were not especially unusual. Indeed, in recent years it has become platitudinous to observe that, in Britain during the early 1800s, a binary view of the arts-sciences divide was not conventional, since, as David Knight and others have emphasised, “polymaths were not uncommon [...] taking a wide range was an acceptable and expected thing to do [... and specialisation] was not yet necessary for success in the sciences” (Knight 1998, 48). As a result of this diversity, the generation immediately preceding Hamilton had produced a number of poet-scientists, of which Erasmus Darwin (1731-1802) and Humphry Davy (1778-1829) are only the most conspicuous examples.[7] Nevertheless, despite the prevalent advocacy of versatility, an implicit cultural polarisation of the kind implied in Wordsworth’s 1831 letter seems already to have infiltrated Hamilton’s mediations upon the subject by the late 1820s, though he resisted a mutually exclusive apportioning of his scientific and literary interests. For instance, in the final stanza of ‘To Poetry’, he implies that he has resolved to renounce poetry for science, while hinting in quasi-mystical language that such a renunciation is futile:
Graves I, 317Spirit of Beauty! Though my life be now
Bound to thy sister Truth by solemn vow;
Though I must seem to leave thy sacred hill,
Yet be thine inward influence with me still:
And with a constant hope inspire,
And with a never-quenched desire,
To see the glory of your joint abode,
The home and birth-place, by the throne of God!
The central dilemma is here expressed as a choice between “Truth” (presumably, either mathematics or, more generally, science) and “Beauty” (presumably, either poetry or, more generally, literature), but the suggestion is that the mutual exclusivity of these alternatives is only apparent, not real. Indeed, the underlying, visionary implication of the stanza is that mathematics/science and poetry/literature share a common divine dwelling place. Given this close association, it is possible to pursue truth guided by the “inward influence” of beauty (and, presumably, vice versa), and the use of the epistemic verb “seem” to describe the departure from Parnassus (“I must seem to leave”) merely emphasises the fact that the displacement is not actual. The implication is that, guided by the influence of poetry, one may eventually perceive the intrinsic unity of truth and beauty when one arrives at their heavenly location beside the “throne of God”, and this transition from binarity to unity is subtly rendered by the possessive adjectives which shift from the second person singular forms “thy” and “thine” to the second person plural form “your” as the ‘Spirit of Beauty’ and the ‘Spirit of Truth’ approach each other more nearly.
Obviously, the simple assertion that truth and beauty are similar (or even identical) had already become a rather hackneyed poetic cliché by the late 1820s, and while it is certainly intriguing to find a contemporaneous poet-scientist also explicitly probing this association, it is not especially atypical.[8] For instance, in the early 1800s, Davy had expressed similar sentiments in a lecture concerning the relationship between science and art:
In the truths of natural science there is, perhaps, a nearer analogy to the productions of the refined arts. The contemplation of the laws of the universe is connected with an immediate tranquil exaltation of mind, and pure mental enjoyment. The perception of truth is almost as simple a feeling as the perception of beauty; and the genius of Newton, of Shakespeare, of Michael Angelo, and of Handel are not very remote in character from each other.
Davy, 307
Clearly, Davy is here primarily concerned with the subjective psychological effects provoked by the consideration of the objects that have been produced by processes of scientific and artistic creation, an issue that will be discussed in more detail later. Davy identifies a similarity in the manner in which manifestations of truth and beauty are perceived, and this suggests that the two domains are related in terms of the impact they exert upon the mind of the individual who encounters them. Crucially, though, Davy does not assert the complete equivalence of “the perception of science” and “the perception of beauty”, preferring instead to classify the association as being analogical, with the consequence that the psychological experiences induced by these two domains are merely “almost” the same. Complete identity is denied, only similarity remains, and therefore scientific genius (as manifest in Newton) is simply “not very remote in character” from artistic genius (as manifest in Shakespeare).
Although it is not known whether Hamilton was familiar with Davy’s published writings concerning such topics, he too certainly resisted the specific conclusion that mathematics and poetry are absolutely identical. Instead, as indicated above, he usually claimed that, though seemingly separate, truth and beauty emanate from the same source, and that, although the full nature of this interconnection may never be fully revealed or comprehended in this world, it can (it seems) be glimpsed. In an introductory lecture on astronomy, which he delivered in 1830, Hamilton was more explicit still, stating of truth and beauty that
[...] we are compelled to consider these two great objects of admiration to the intellect and heart of man as having connexion indeed and harmony, but not identity. We must separate them, the one from the other, and fix our mental gaze on one alone, and press forward to this one mark, though we love the other not the less, and though its secret presence may attend and cheer us on our journey.
Graves I, 499
Apparently, it was this continued belief in the intrinsic, contrasting complementarity of mathematics and poetry (the two disciplines that he associated most closely with truth and beauty, both respectively and interchangeably) that caused Hamilton to place them on the same level of “the ascending hierarchy of human thought” which he constructed rather grandly in 1830 (three years after writing ‘To Poetry’, and one year before he received career advice from Wordsworth). Specifically, the hierarchy he devised was as follows (415):
Religion
Metaphysics
Mathematics and Poetry
Physics and Literature
Physics and literature occupy the lowest level, presumably because they are the most earth-bound: physics necessarily involves empirical confirmation, the grubby probing of the natural world, while literature, although a profoundly problematical term in the early nineteenth century,[9] surely refers to prose here (otherwise it would not be distinct from poetry). As Wordsworth’s 1831 letter indicates, prose was still generally considered at this time to be a path that could be trodden with “footsteps less careful”, hence its lowly status in Hamilton’s pyramid. Continuing upwards, the next level contains mathematics and poetry, so presumably he considered these disciplines to be more refined, more ethereal than physics and literature respectively, and they both point towards metaphysics, which in turn leads directly towards religion, the apogee of the structure.
In 1830, then, Hamilton claimed that mathematics and poetry occupied the same position on the hierarchy of human thought. Significantly, like Davy, Hamilton seems to have been persuaded that the psychological consequences of encountering creative work in mathematics and poetry were similar in many respects, and this may have been one of the factors that caused him to juxtapose the two disciplines. For example, in a 1832 astronomy lecture, he noted:
With all the real differences between Poetry and Science, there exists, notwithstanding, a strong resemblance between them; in the power which both possess to lift the mind above the dull stir of earth, and win it from low-thoughted care; in the enthusiasm which both can inspire, and the fond aspirations after fame which both have a tendency to enkindle; in the magic by which each can transport her votaries into a world of her own creating; and perhaps, in the consequent unfitness for the bustle and the turmoil of real life, which both have a disposition to engender.
652
In recent years there has been a tendency to disassociate Romantic poetry both from the avoidance of social reality and from the desire to escape into inner realms of subjectivity, and this development was partly a therapeutic reaction against certain critical stances that had become conventional in the early twentieth century. For instance, in 1937 Christopher Caudwell suggested (rather prettily) that the narratorial voice of Keats ‘Ode to a Nightingale’ “escapes upon the ‘rapid wings of poesy’ to a world of romance, beauty, and sensuous life separate from the poor, harsh, real world of everyday life, which it sweetens and by its own loveliness silently condemns” (Caudwell, 108), while, four decades later, John Fekete similarly emphasised the private, escapist tendency of Romantic literature which frequently manifests “a disaffection from society” (Kekete 1976, 6). Naturally enough, since the 1970s, there have been several revisionist attempts to demonstrate that, on the contrary, Romantic literature is profoundly interconnected with social-political concerns. As Daniel Watkins has remarked, “the social and historical dimensions of poetry are not to be determined solely by an author’s expressed interest in the connections between poetry and social reality” (Watkins 1989, 11). Nonetheless, despite this, the critical readings which focus on the fantastic and magical aspects of Romantic poetry certainly chime with Hamilton’s assertion that poetry and science both seek to “lift the mind above the dull stir of earth and win it from low-thoughted care”. It is of particular interest that he uses the word “enthusiasm” in this context, since this problematical noun figures prominently in his discussions of science and poetry.[10] For instance, in an 1832 lecture, he defined enthusiasm as “highly to conceive, intensely to admire, and ardently to aspire after excellence” (Graves I, 652), and he maintained that the enthusiastic pursuit either science or poetry enables the suppliant to transcend the tawdry and the mundane. Intriguingly, the claim that mathematics and poetry both distract by offering relief from reality appears repeatedly in Hamilton’s writings. For example, his descriptions of mathematical and poetical creation frequently refer to praeternatural domains that are somehow removed from conventional sensory experience. In one 1825 poem, for instance, he writes:
195Yet ‘twas the hour the Poet loves
Alone to wander through the groves;
Unheeded, uncontroll’d to pour
His spirit forth in verse; to soar
Up to the heaven of heavens; to climb
Above the bounds of Space and Time;
To call ideal worlds to view,
His own creation bright and new.
The desire to escape is here figured as an ascent involving the exploration of “ideal worlds”, and the urge to “climb/Above the bounds of Space and Time” articulates a longing for transcendental liberation even from the sorts of universal spatio-temporal constraints that were standardly postulated in Newtonian mechanics in the early ninteenth century (as Hamilton, of course, knew well).
For Hamilton, therefore, poetry and mathematics were related by their capacity to facilitate a transition from the actual to the imaginary in such as way as to accomplish the etherealisation of, if not a comprehensive evasion of, the dilapidated and the partial. In fact, his remarks occasionally imply that the more impossible the act of liberation, the more thrilling and satisfying the endeavour; and this emphasis on the pleasure induced by feats of mathematical and poetical escapology recurs persistently in Hamilton’s work. For instance, he was fascinated throughout his life by the nature of mathematical infinity.[11] In particular, although fully aware of the paradoxes and perplexities that beset this subject, he recognised both that the notion of infinity forces us to strive beyond the common realms of experience, and that the consideration of such imponderables was a noble and delectable pursuit. He maintained that a “Science of the Infinite” was theoretically feasible, and he associated the concept of infinity directly with that of beauty, once again adopting an aesthetic stance in relation to a mathematical subject. Specifically, in an 1829 Memorandum that was written while he was sketching out a response to an antagonistic letter from Francis Edgeworth (1774-1857), Hamilton commented as follows:
Perhaps you may be right in your opinion that every beautiful object in finite; but the higher orders of Beauty seem at least to suggest infinity, and even, were Beauty always and altogether finite, Power is otherwise. Nor can I admit that there is not a pleasure, and a very intense one, in endeavouring to grasp infinity, or at least in meditating on such things as most suggest it.
349
So, the pursuit of (unattainable) infinity inspires a sensation of pleasure principally because it necessitates the confrontation mental (and perhaps spiritual) limitations, and explorations of such themes were common in the poetry of the early nineteenth century. Indeed, the cognitive consequences of the way in which the notions of spatial and temporal infinity were manipulated in the literature of the period have been discussed in several monographs, and Reuven Tsur’s Towards a Theory of Cognitive Poetics (1992) sketches a framework for assessing these themes.[12] Reference to infinity, though, and not hard to find in Romantic texts. For example, in The Prelude, Wordsworth declares that “Our destiny, our nature, and our home/Is with infinitude, and only there”, adding that the attempt to strive towards such things causes the mind to experience an “access of joy” (Wordsworth, 100). Similarly, there are Shelley’s lines in A Defence of Poetry which associate poetry (in particular) closely with infinity: “All high poetry is infinite; it is as the first acorn, which contained all oaks potentially. Veil after veil may be undrawn, and the innermost naked beauty of the meaning never exposed” (Reiman and Fraistat 2002, 528). While neither of these examples refers explicitly to scientific research, it is crucial to stress that Hamilton’s depiction of hedonistic scientific labour was not without precedents either. For instance, the general belief that pleasure was a fundamental aspect of both literary and scientific experience had been emphasised by Wordsworth as early as 1802 in the Preface to the second edition of Lyrical Ballads. In this text, he claimed that “the knowledge both of the Poet and the Man of Science is pleasure” (Wordsworth and Coleridge, 76), and it should be remembered that, in writing this, he was possibly guided by Humphry Davy, with the result that Davy’s thinking concerning this matter may have influenced Wordsworth directly.[13]
In summary, then, Hamilton considered mathematics and poetry to be profoundly and intricately intertwined: if the two disciplines are understood to emanate from the same divine source, then, although distinct, they can be said to share a common origin, and, given this, it is no surprise that a focused study of these two branches of learning should culminate in comparably pleasurable displacements which enable the burdensome drudgery of daily life to be evaded. So far, this brisk overview has not focused on the role of the creative imagination in the processes of literary and scientific composition, yet, given the centrality of this issue in Hamilton’s thought, it must be assessed before his further claim that mathematical treatises can be viewed as ‘poetical’ texts can be adequately evaluated.
III. A Formable Matter
As indicated previously, Hamilton reflected upon the nature of the relationship between mathematics and poetry throughout his life, and he repeatedly attempted to elucidate their “mysterious and intimate connection” (Graves I, 347). In particular, during the late 1820s, he began to argue that the role of the creative imagination was a distinctive defining characteristic of both disciplines, a view that he maintained for the rest of his life. Apparently, an epistolary interchange with his playfully antagonistic friend Francis Edgeworth prompted him to probe this subject more seriously.[14] Edgeworth was an ardent Platonist who, in a letter written in August 1829, provokingly derided science as merely servile empiricism while claiming that mathematical truth was a meagre form of truth at best which does not deserve to be associated with a concept of such nobility as that of beauty: “Why”, Edgeworth had enquired, “is the study of beauty higher than that of mathematical truth? […] they certainly appear distinct from each other” (340). As a professional scientist, Hamilton felt obliged to rebut Edgeworth’s teasing criticisms, and he did so by emphasising the essential creativity of mathematics. More specifically, having restated his conviction that truth and beauty, though different, are inherently related, he proceeded to argue that mathematics can be analysed in relation to both:
[...] I must say that I believe myself to find in mathematics what you declare you do not – a formable matter out of which to create Beauty also; and that, to my particular constitution of mind, a mathematic theory presents even more of the “intense unity of the energy of a living spirit” than the work of a poet or an artist.
348
The central assertion here is that a creative process of some sort can indeed manipulate the “formable matter” of mathematics, and Hamilton clearly stresses this in order to convince Edgeworth that pure mathematics (at least) is more than mere servile empiricism.[15] In essence, according to Hamilton, a (pure) mathematician does not passively observe, rather such a person actively generates new abstract structures and ideas which possess an internal coherence that is not necessarily substantiated or corroborated by means of experimental procedure. The implication, therefore, is that it is the very malleability of mathematics that enables it to be considered in terms of beauty since (so Hamilton implies) all created objects possess an inherent aesthetic value whether they are works of mathematics or works of poetry (or, presumably, creative works of any other kind). Hamilton’s assertion, therefore, is that the task of constructing a mathematical theory is an even more creative activity than the task of writing a poem, and consequently, as a creative enterprise, it reveals more of the “intense unity of the energy of a living spirit” than poetical composition. Indeed, Hamilton was so preoccupied with these issues at this period of his life that he did not only seek to change the mind of Francis Edgeworth, but also that of Francis’ sister, the novelist Maria Edgeworth (1767-1849). By the time Hamilton made her acquaintance, Maria was already a celebrated writer who espoused a rather parsimonious view of science. However, Hamilton was persuasive, and, in an 1831 letter, Maria wrote “I am glad to see it proved that the severe sciences do not destroy the energy and grace of the imagination, but only chasten and impart their philosophical influence” (468).
Perhaps it is not surprising that the creative imagination should have become a central aspect of the argument Hamilton constructed in order to refute Edgeworth, since (as is well known) the nature of the imagination had been a topic of fierce debate amongst European intellectuals since at least the late seventeenth century; and the advent of German Idealism had prompted a refocusing of the discussion.[16] Although the influence of transcendental (and absolute) idealism upon the so-called ‘Romantic scientists’ of the early 1800s has become a contentious issue, it is clear that Kant’s writings in particular exerted a direct influence over Hamilton.[17] While this is not the place for a detailed discussion of Hamilton’s familiarity with the various flavours of idealism, it is worth noting that he first read Kant in 1834 (in German, since, unlike Davy and Michael Faraday (1791-1867), the polyglot Hamilton was able to read the untranslated texts with reasonable facility), and the extent of Kant’s influence cannot really be underestimated. In later life, Hamilton freely admitted that he had “a leaning to Idealism”[18] and it has been suggested that Kant’s arguments concerning spatial and temporal intuition were largely responsible for determining Hamilton’s own approach to algebraic systems.[19] Although, Kant never formulated definite conclusions concerning the role of the imagination in scientific research, his writings certainly directed Hamilton’s attention towards such topics, though it is important to stress that Kant was not the only person whose writings influenced Hamilton’s thinking concerning this matter. For instance, although it is not known for certain whether Hamilton studied the writings of Johann Gottlieb Fichte (1762-1814) and Friedrich Wilhelm von Schelling (1775-1854) in comparable detail, he certainly seems to have encountered their work in one form or another for he explicitly noted the emphasis placed upon the centrality of the creative mind in their writings. For example, in an 1834 letter to H.F.C. Logan he writes,
The more I reflect upon the theory of Idealism, the more inclined do I feel (with some modifications) to receive its dogmas, and believe with Berkeley and Fichte (Grundlage der gasammten Wissenschaftslehre, Die Bestimmung des Menschen – there is a French translation of this under the title Destination de l’Homme) that the phenomena of the external world and their laws are the produce of the mind itself.
Graves II, 86
There is evidence, however, that Hamilton’s knowledge of absolute idealism had not been obtained directly. In another 1834 letter to Logan, for instance, Hamilton declares “Schelling, however, I still have a greater desire to study than Fichte” (87), implying that, at least in 1834, he had not studied either directly, and certainly it is the case that he discusses their work less frequently in his correspondence than he discusses the work of Kant. Nevertheless, even if Hamilton never studied Fichte and Schelling at length, he clearly glimpsed something of their work in the writings of Samuel Taylor Coleridge (1772-1834) who was one of the most conspicuous propagators of German idealism (both transcendental and absolute) in Britain in the early 1800s. Crucially, Hamilton’s familiarity with Coleridge’s work was not confined merely to library perusings since the two men met several times, and, given this association, it is no surprise that Coleridge’s complex views concerning the role of the creative imagination in scientific research appear to have influenced Hamilton.[20] In particular, Coleridge had been persuaded by Davy in the early 1800s that science was more than an unimaginative, mechanistic enterprise, and this realisation compelled him to reconsider the role of the imagination in scientific research.[21] For instance, to consider a familiar example, in Aids to Reflection, Coleridge described how he had come to admire Kepler’s scientific work above Newton’s primarily because he considered the former to be characterised by true creative imagination while the latter was largely collective. In other words, Coleridge maintained that, unlike Kepler, Newton had merely synthesised existing ideas and had not generated any new concepts of his own, therefore his work should be viewed as a lesser procedural methodology that could be associated with fancy rather than with imagination, at least as these are defined in the Coleridgean classificatory schema.
Influenced, therefore, by the work of Kant, Fichte, Schelling, and Coleridge, Hamilton began in the 1830s to muse upon the workings of the creative imagination both in scientific research and literary composition. For instance, in an astronomy lecture delivered in 1832, having stated that the imagination was implicated in all scientific research, Hamilton continued:
Be not startled at this, as if in truth there were no beauty, and in beauty no truth; as if these two great poles of love and contemplation were separated by a diametrical space, impassable to the mind of man, and no connecting influences could radiate from their common centre. Be not surprised that there should exist an analogy, and that not faint or distant, between the workings of the poetical and of the scientific imagination; and that those are kindred thrones whereon the spirits of Milton and Newton have been placed by the admiration and gratitude of man.
652
Intriguingly, the language of this passage is conspicuously similar to that of Davy’s lecture quoted earlier. Once again an “analogy” is posited between truth and beauty, and once again the achievements of a great writer (i.e., Milton) and great scientist (i.e., Newton) are juxtaposed. However, Hamilton augments the basic argument by explicitly distinguishing between the poetical and the scientific imagination, and although these contrasting types are considered to be separate, they are nevertheless understood to share a “common centre”. Consequently, as in ‘To Poetry’, written three years previously, Hamilton here claims that truth and beauty achieve some kind of (analogical) correspondence through the similarities inherent in the creative imaginative processes associated with the production of mathematics and poetry.
While Hamilton’s emphasis on the role of the creative imagination in the generation of mathematics and poetry was no doubt prompted in part by his “leaning to Idealism”, he also seems to have been influenced by his own personal experience of creativity in both fields. This point is worth stressing since, by the time he delivered the 1832 lecture discussed above, he had already written numerous poems and had made several innovative contributions both to (pure) mathematics and to mathematical physics. Indeed, Hamilton occasionally discussed his own personal creative experiences in his correspondence, frequently stressing the role of initial inspiration. For instance, he seems to have become convinced in the 1820s that the finest poetry is usually produced when an incommunicable momentary inspiration is followed by careful subsequent reconsideration, though such reflection may never enable the initial insight to be conveyed:
A poet can never fully express what he feels in the happy moments of inspiration; hence independently of the effect of his parental fondness for his own writings, they cannot communicate to others the same train of ideas which they awaken in his mind.
116
This predominantly melancholy passage implies that the poet is unable to “express what he feels” while in a state of inspiration, and therefore he must accept that his poems will never recreate an identical “train of ideas” in the mind of the reader. Although more pessimistic in tone, such passages clearly recall Wordsworth’s observation that poetry “takes its origin from emotion recollected in tranquility” (Wordsworth and Coleridge, 82), and although it is certainly possible that Hamilton is here merely outlining a Wordsworthian stance concerning the relationship between inspiration and composition, this kind of observation certainly suggests that, for Hamilton, inspiration was a crucial initial stage in the process of poetical composition. Given this brief summary, it is fair to claim that there is little that is remarkable in Hamilton’s views concerning the role of the creative imagination in the production of poetry. What, though, of his views concerning the role of the creative imagination in the context of scientific research?
Although Hamilton discussed scientific creativity on several occasions, his most explicit remarks are contained in his accounts of the development of his beloved Quarternions. Briefly, the story runs as follows. In 1831, Hamilton had commenced serious research into the foundations of the real number system, and he eventually published the results of his research as A Preliminary and Elementary Essay On Algebra as the Science of Pure Time (1837). This work required him to investigate the properties of imaginary numbers in considerable detail and he tried to develop a three-dimensional counterpart of complex number theory. Unfortunately, his attempts were continually thwarted because he was unable to define multiplication in a satisfactory manner. Writing in 1858, fifteen years after the event, he recalled the moment of creative insight during which he had realised that the hypercomplex numbers he sought required four rather than three imaginary parts:
Tomorrow will be the 15th Birthday of the Quarternions. They started into life full grown on the 16th of October, 1843, as I was walking with Lady Hamilton to Dublin, and came up to Brougham Bridge, which my boys have since called the Quaternion Bridge. That is to say, I then and there felt the galvanic circuit of thought close; and the sparks which fell from it were the fundamental equations between i, j, k; exactly such as I have used them ever since. I pulled out on the spot a pocket-book, which still exists, and made an entry, on which, at that very moment, I felt that it might be worth my while to expend the labour of at least ten (or it might be fifteen) years to come. But then it is fair to say that this was because I felt a problem to have been at that moment solved – an intellectual want relieved – which had haunted me for at least fifteen years before.
Graves II, 435-436
Essentially, on that remarkable day, Hamilton realised that he had to utilise quadripartite hypercomplex numbers such as Q, where Q = α + βi + ci + δi, α, β, c, and δ are real numbers, and i = √-1. The primary mathematical significance of such numbers was that they permitted the development of a non-commutative algebra. In other words, unlike conventional algebras, if Q1 and Q2 are both Quarternions, then Q1 Q2 ≠Q2 Q1. While Hamilton’s account of his moment of creative insight is a typical example of instantaneous inspiration, it is noteworthy that, in his retrospective version of the event, he claims that he recognised the need for further development of the essential ideas that had been garnered in an instant. A definite conclusion (i.e., a set of specific equations) had been obtained in a moment of quasi-mystical insight, and not as the result of an arduous process of axiomatic-deductive inference, and experiences such as this convinced Hamilton that the scientific imagination can be associated with moments of inspiration in a similar manner to the poetical imagination. In addition, as noted above, he recognised that both kinds of inspiration required lengthy subsequent labour in order to render a finished created work. So, crucial as they are, the instants of inspiration that characterise both mathematical and poetical creativity merely constitute the beginning of the creative process, and Hamilton’s most remarkable pronouncements concerning the relationship between mathematics and poetry concern the manner in which mathematical and poetical texts are constructed once a given moment of initial inspiration has passed.
IV. A Kind of Scientific Poem
During his lifetime, Hamilton was referred to as “the Irish Lagrange” (De Morgan, 128) – an appropriate epithet, since his most important contributions to analytical dynamics were directly inspired by the work of Joseph-Louis Lagrange (1736-1813).[22] In particular, Hamilton was inspired by his study of Lagrange’s Mécanique Analytique (1788), a monumental text which effectively demonstrates that statics (i.e., the study of systems of bodies that are in equilibrium) and dynamics (i.e., the study of systems of bodies that are in motion) can be reduced to one fundamental principle – namely, ‘le Principe des Vitesses Virtuelle’.[23] Consequently, Lagrange’s treatise is neatly divided into two main parts, appropriately entitled ‘statics’ and ‘dynamics’, and, by convincingly unifying these two traditionally separate branches of mathematical physics, he inspired a whole generation of scientists to refine and elaborate the mathematical framework for analytical mechanics that he had constructed.
Hamilton first studied Lagrange’s work at the age of 17, returning to it as a source of inspiration throughout his life, and his admiration was entirely justified since the latter was undoubtedly one of the finest scientists of the eighteenth century. Specifically, the depth of Hamilton’s veneration for his illustrious predecessor is stated explicitly in the preface to his most celebrated paper On a General Method in Dynamics, when, having discussed the contributions to the study of motion made by Galileo and Newton, Hamilton goes on to remark:
Among the successors of those illustrious men, Lagrange has perhaps done more than any other analyst, to give extent and harmony to such deductive researches, by showing that the most varied consequences respecting motions of systems of bodies may be derived from one radical formula; the beauty of the method so suiting the dignity of the results, as to make of his great work a kind of scientific poem.
Hamilton 1834, 248
The “work” referred to in the above quotation is Lagrange’s Mécanique Analytique (1788), and Hamilton’s comments provide insights into his particular conception of poetical mathematics. For instance, he refers explicitly to those sections of Lagrange’s work which demonstrate that the motion (and equilibrium) of a system of bodies can be analysed fully using only “one radical formula”, and he stresses that the poetry of these sections of Lagrange’s text is manifest in two specific aspects of the work – namely, in the beauty of the “method” employed and in dignity of the “results” obtained. Obviously, before proceeding further, it is necessary carefully to consider these two features of Lagrange’s work separately.
In common nineteenth-century usage, the word “method” could refer to “specific procedures in mathematics and experimental science” (OED) and this included the axiomatic-deductive methodology that had figured so prominently in mathematical and scientific treatises ever since Euclid (and, most likely, before). Consequently, the term ‘method’, as Hamilton uses it in the preface to his 1834 paper, referred particularly to the manner in which specific mathematical ‘results’ (or theorems) were derived, hence his distinction between the method used and the particular results obtained. Importantly, in later life, Hamilton prioritised mathematical method over mathematical results, claiming that the structure of a given argument was of greater importance than the resulting theorems. For instance, in a letter written in 1858, he requested that one of his own theorems should not be referred to as “Hamilton’s Theorem”, and he explains this seemingly perverse aversion as follows:
I hope, indeed, that it may not be considered as unpardonable vanity or presumption on my part, if, as my own taste has always led me to feel a greater interest in methods than in results, so it is by METHODS, rather than by anyTHEOREMS, which can be separately quoted, that I desire and hope to be remembered.
Tait, 50
Unlike a “method”, any particular theorem can be extracted from out of its immediate context and used in isolation from the body of a work in which it was initially embedded with the result that the argument which established the theorem is entirely neglected. Seemingly, for Hamilton, the method deployed in a scientific/mathematical treatise largely determined the organic structural unity of the whole, and, since he preferred results to be considered in context, he consistently advocated the appreciation of method. Given this predilection, therefore, it is not surprising that he should identify Lagrange’s method as being a crucial component of Mécanique Analytique. But exactly which kind of method did Lagrange use in his treatise and why did Hamilton consider it to be especially poetical?
Unsurprisingly, in true Euclidean-Newtonian fashion, Lagrange had employed the axiomatic-deductive method in Mécanique Analytique in order to present his results. He begins by stating principles that are assumed to be true, and then proceeds to construct a range of theorems that follow as a result of these principles; each new section extends the analyses that have been developed in the preceding sections, and the various formulae presented are introduced in ordered succession. The formal methodology Lagrange employed was common to many eighteenth-century scientific treatises and therefore, since Hamilton did not consider all treatises that used the axiomatic-deductive method to be poetical, it is clear that he did not consider the method itself to be inherently beautiful. Rather, he appears to assess each particular use of this method in accordance with an (informal) aesthetic criterion. In other words, from Hamilton’s perspective, it is not enough simply to derive correct theorems from given assumptions, it is necessary also to derive the theorems in a beautiful manner. If this is correct, then mathematical proofs can no longer simply be produced in a mindless, mechanical fashion, since it is possible for a proof to be ugly even though it may be valid. Clearly, Hamilton appears to be suggesting that there are fundamental aesthetic considerations which are central to the whole mathematical enterprise. Indeed, in many respects, he appears to be anticipating the stance advocated by G.H. Hardy who observed in A Mathematician’s Apology (1940) that “there is not a permanent place in the world for ugly mathematics” (Hardy, 25).
Hamilton’s view of mathematical method, as summarised above, may be disconcerting, yet it is well-established that he had been fascinated by the methodology of axiomatic-deductive systems since his teens. For instance, in a remarkable early essay written in 1822, he explicitly considered the complexities involved in constructing an axiomatic-deductive presentation. The essay in question, A Waking Dream, takes the form of a Platonic dialogue in which Pappus (Hamilton) interrogates Euclid concerning The Elements. In this work, Hamilton explores the differences that exist between the discovery procedures that enable a proof for a particular theorem to be constructed and the formal presentation of the proof as it is offered in the context of an axiomatic-deductive treatise. Indeed, Pappus’ very first question to Euclid explicitly addresses this issue:
[...] permit me to inquire how you were enabled to deduce consequences so remote from principles so simple: inform me what it was that first suggested to your mind the consideration of those Theorems which have come down under your name? For so successful have you been is disguising the Analysis which you pursued, that to this day even the learned are doubtful whether your discoveries were made by a gradual process, like that which conducts to truths minds of other men: or whether they were imparted as an immediate gift from Him who constructed for the Bee its wondrous habitation.
Graves I, 662
Pappus here wishes to appreciate the nature of the discovery procedures that Euclid employed in order to create the structure of the axiomatic-deductive proofs presented in The Elements: were the principles and theorems obtained gradually, in a slow heuristic fashion which involved repeated revisions and reconsiderations, or did the whole work emerge fully formed in a single instant of inspiration (in the manner of Hamilton’s Quarternions)? From the outset therefore, Pappus is particularly concerned with the process of mathematical creation, and his probing of this issue swiftly starts to reveal fissures that separate the process of mathematical discovery from the formal presentation of mathematical arguments in the form of a treatise such as The Elements. This concern is revealed in the above quotation when Pappus mentions the “disguising” that Euclid deployed in order to conceal the actual stages in his “Analysis”, and the central issue here involves the nature of the deceit that is inevitably perpetrated in any mathematical treatise. Such deceit is unavoidable simply because a formal presentation of a mathematical argument never reveals the particular lines of reasoning that actually led to the creation of the argument: once a theorem has been proved, the proof is then refined and presented in an enticing manner that captivates and enchants. Pappus’ enquiries are undeniably searching, and Euclid responds to questions of this type with true candour, discussing the genesis of The Elements with remarkable honesty:
It was not unintentionally that I adopted, as the medium of communicating to my contemporaries those results at which I arrived, a Synthesis, which presented them under a form the best adapted to excite astonishment, and to disguise the process of discovery. To exoterics the science appeared more interesting as it was more mysterious: and for myself – if the world had known all the fortuitous circumstances to which I owed the perception of so many Theorems, would they have reverenced as they did the Mathematician of Alexandria? […] The inventor of a curious piece of mechanism does not expose his artifice to the vulgar eye; nor does an architect, when he has erected a magnificent edifice, leave the scaffolding behind [...].
662[24]
In this reply, Euclid readily acknowledges that, as Pappus had insinuated, deceit is indeed a crucial aspect of mathematics. Further, he freely confesses that one of his intentions when devising the final form of The Elements was to “disguise the process of discovery”, and one (desirable) consequence of this was to cause the whole work to seem “mysterious” so that it would engender “astonishment” in his audience. Given Hamilton’s interest in the interrelations between mathematics and poetry, it is of considerable interest that his fictional Euclid is inclined to view mathematical treatises almost as if they were literary texts which seek to delight and beguile readers. Specifically, Euclid’s comments suggest that the most effective mathematical arguments manipulate the presuppositions and expectations of the intended audience in order to generate wonder, awe, and, presumably, amusement.[25] However, although Pappus accepts this, he is still preoccupied with the actual discovery procedures that Euclid used, and consequently he asks about the genesis of the definitions, postulates, and axioms that Euclid employed. In particular, he wishes to know “by what intuition you selected a priori all that could be necessary or useful and nothing besides?”. Once again, in replying, Euclid emphasises the fact that the construction of an axiomatic-deductive system is in essence an heuristic art form:
You are not to suppose that they were received at once, or as you have expressed it a priori, that form in which they now appear. The Definitions arose, some out of necessity of making my own ideas precise, and of communicating them to others; some I introduced that I might from the statement of a simple property deduce by geometrical reasoning properties less obvious and remote; some were suggested by analogy, and others invented afterwards, to present under a more systematic form the introduction to the science. In a word, no part of the The Elements has received more alterations as I proceeded than the collection of Definitions with which they commence. [...] The Postulates were at one time more numerous than they are now. It was not at once that I perceived the smallest number of data that were sufficient to resolve all geometrical problems, and effect all geometrical constructions. But with respect both to them and to the Axioms, I may observe, that they were not formed, as you seemed to suppose, a priori, but as occasion offered.
663
Euclid’s position here is clear: mathematics is being viewed as an experimental science, and therefore it is a domain in which trial and error are continually used in order to obtain results – an approach which in turn indicates that the structure of a given axiomatic-deductive system is modified repeatedly as it is adapted in order to account for the specific relations it seeks to describe. Consequently, rather than being viewed as a static structure of inter-related eternal truths, mathematics is here presented as a dynamic process of protracted redefinition and adaptation.[26]
In order to elaborate this point, Hamilton allows his fictional Euclid to reflect upon particular details of the manner in which his arguments developed while The Elements was in the process of being constructed. For instance, Euclid recalls that a number of the definitions, postulates, and axioms that he eventually stated at the beginning of his text were actually introduced retrospectively, as a direct result of the need to produce a proof for the first proposition, which requires the construction of an equilateral triangle,[27] and he recollects the way in which he came to realise that, given a straight line AB, it was not possible to find a point C such that C was equidistant both from A and B simply by drawing a line the length of which was equal to AB. As he acknowledged, such a simplistic approach would not work since an infinite number of such points exist. However, once this insight had been reached, Euclid was able to state the fundamental property of a circle – namely, that the radii of a circle are all equal, and therefore he was able to add definitions 14, 15, 16, and 18 to his exposition.[28] Having established these definitions, Euclid recalls that he continued with the task of constructing a proof for the 1st proposition, and, when he realised that, in order to construct an equilateral triangle on the given line AB, he needed to be able (i) to draw a straight line between any two given points, and (ii) to draw a circle with any given centre and radius, he subsequently modified the existing set of postulates by adding postulates 1 and 3.[29] By recalling these steps in the process of discovery, Euclid seeks to reveal to Pappus (Hamilton) the manner in which the eventual structure of The Elements was created. In particular, he indicates that the sets of definitions, postulates, and axioms were continually modified, revised, and expanded as proofs were sought for the various propositions with the result that the sequential ordering of the mathematical argument presented in The Elements differs greatly from the order in which the various ‘discoveries’ were made. For instance, when Pappus enquires as to the ordering of the 4th and 5th propositions, Euclid states of the former
Although that celebrated theorem occurs the first in the synthetic arrangement, it was not the first in the order of my thoughts. That rank belongs to the 5th proposition, or rather to a particular case of it, namely, that the base angles of an equilateral triangle are equal.
666
It is Hamilton’s awareness of the distinction between the “synthetic arrangement” of an axiomatic-deductive treatise and its actual arrangement (i.e., the actual order in which the definitions, postulates, axioms, and propositions were devised) that enables him to recognise the beauty of such works. A reader of a treatise such as The Elements will encounter ideas in the definitions, postulates, and axioms, that perhaps seem needless initially, yet, as the argument develops and the various propositions are established, the utility of the initial components should become clear – and no doubt it is this that eventually produces “astonishment” in the intended audience since it gives the impression that all possible future exigencies were anticipated at the very outset.
Apparently, then, A Waking Dream demonstrates that, while still a boy, Hamilton was fascinated by the idea that formal presentations of axiomatic-deductive systems artfully disguise the tortive intricacies of their own construction, and therefore he was able to appreciate the astonishing imagination, intelligence, and sheer creative exuberance that were required in order to deploy the method with rigour and panache. Consequently, he recognised that even the finest treatises in applied (rather than pure) mathematics which make use of well-constructed axiomatic-deductive arguments possess an additional aesthetic quality, such that the abstract formal beauty and coherence of such a system can be valued in its own terms whether or not it accurately models those phenomena occurring in the external world which it was devised to describe. No doubt it is this understanding that prompted Hamilton, in the letter to Edgeworth discussed previously, to remark of Newton’s Principia:
Even the “Principia” of Newton, which is ordinarily perused as a model of inductive philosophy, I consider as being rather a work, a fabric, an architectural edifice, the external results of which have been and will be changed by the progress of experimental science, but which will always be interesting to a mathematician as a structure of beautiful thoughts.
348
This is a startling observation, especially since it was written by one of the leading physicists of the early nineteenth century. Obviously, the most prescient asseverations here are that the formal structure of Newton’s axiomatic-deductive treatise is a thing of beauty in and of itself, and that its inherent aesthetic value is not undermined even when it is demonstrated that the results (i.e., the theorems or laws presented in the treatise) are empirically invalid. Consequently, it is this intrinsic beauty, which arises from the ingenious construction of an axiomatic-deductive treatise such as the Principia, that endows such works with a methodological grace that is akin to poetical beauty. Two years later, in one of his lectures on astronomy, Hamilton elaborated further upon his appreciation of the artistic aspects of Newton’s work when, having outlined the approaches to astronomy that dominated in the fifteenth and sixteenth centuries, he continued:
Then Newton came; he felt that power not less than beauty was an object of the intellect, that the unity of law, as well as that of form, could make the Infinite, One; he framed therefore a universe of energies; or rather, as the mind of an artist calls up many forms, he meditated on many laws and caused many ideal worlds to pass before him: and when he chose the law that bears his name, he seems to have been half determined by its mathematical simplicity, and consequent intellectual beauty, and only half by its agreement with phenomena already observed.
502
Yet again the main emphasis here falls upon the prioritisation of simplicity and beauty (of a Shelleyan “intellectual” kind in this case), suggesting that, for Hamilton at least, there was much more to the axiomatic-deductive method than mere axiomatic-deduction: a given theorem may have been correctly derived from given axioms, but this alone will never endow the treatise concerned with formal beauty; rather this quality is established only by the delicacy and subtlety of its construction, and this property remains outside the realm of either deductive or inductive inference. Given Hamilton’s appreciation of Lagrange’s Mécanique Analytique, then, it would appear to be the case that, in Hamilton’s estimation, Lagrange had employed his (axiomatic-deductive) method in such an enticing and artful manner that he had succeeding in producing a formal structure of unusual beauty.
Appropriately, these ideas can be related directly to Hamilton’s appreciation of poetry: if mathematical treatises are viewed as structures of beautiful thoughts, then similarities between mathematics and poetry start to emerge since (obviously) traditional poetical forms impose certain formal constraints upon the poet who, in order to demonstrate mastery of the art, must operate within the confinement of the basic structure in a way that is comparable to the manner in which a mathematician must construct an argument in accordance with the restrictions of the axiomatic-deductive method. It is not surprising, therefore, that Hamilton seems to have been particularly interested in poetical form. In general, he seems to have preferred working within tightly constrained forms, for, although he occasionally wrote in blank verse, and freer ‘Ode’ structures, he primarily produced sonnets, and he consistently manifested an awareness of the precise nature of the restrictions imposed by the particular poetical genre adopted. In one of his 1831 letters to Wordsworth, for example, Hamilton justified his decision in recent poems to flout one of the ‘rules’ that regulated octave structure:
In these I have allowed myself to transgress a rule which seems to be always observed by Milton and you and some other high authorities, namely that of giving a common ending to four of the first eight lines. In excuse I plead that Shakespeare seems never, or scarcely ever, to observe that rule.
488
Clearly Hamilton is here concerned with the implications of the formal structure of the sonnet, and although Wordsworth responded by questioning the wisdom of using Shakespeare as a model, noting that his sonnets are “merely quatrains with a couplet tacked to the end” (493), Hamilton continued to experiment with different formal poetical structures. The essential point, though, is that, like axiomatic-deductive treatises, poems that are written in conformity with a strict formal pattern are not inherently beautiful of necessity, rather their beauty results from the manner in which the constraints are negotiated.
Having discussed Lagrange’s method and issues concerning formal structure in mathematics and poetry at some length, it is important briefly to consider why Hamilton implied that Lagrange’s results were also implicated when he classified Mécanique Analytique as a “kind of scientific poem”. As mentioned previously, the results that Lagrange presents in Mécanique Analytique are the various theorems that he deduces from the fundamental principles (e.g., le Principe des Vitesses Virtuelle) that he states. However, presumably it is the case that theorems which have been correctly deduced from given principles do not themselves inevitably endow an axiomatic-deductive treatise with dignity. Why therefore, in Hamilton’s estimation, do Lagrange’s results manage to accomplish this? In order to answer this question it is helpful to consider a specific example; and certainly one of the most important results in Mécanique Analytique is the derivation of the invariant form of the differential equation of motion which Lagrange’s presents in Part II of his treatise. Presumably, this is the “one radical formula” of which Hamilton speaks with such respect in the introduction to his paper on dynamics (as mentioned above). More precisely, having determined that L = T – V, where, in modern terminology, L is the Lagrange function, T is kinetic energy, and V is potential energy, Lagrange goes on to derive the formula
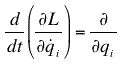
where n specifies the number of degrees of freedom in the system, qi is a generalised co-ordinate with i = 1,2,...,n, and q̇i is the time derivative of qi. The importance of this set of equations lies in the fact that it enables the equation of motion in any system of co-ordinates to be obtained as soon as the expressions for kinetic and potential energy are known. In other words, Lagrange’s accomplishment was to identify and represent in a generalised form the relationship between the equations of motion, kinetic energy, and potential energy, and, in addition, to demonstrate that the same relationship holds in a wide range of disparate physical systems. It seems likely that it is this recognition of identity in apparent difference, along with the simplicity and elegance of its expression, that Hamilton found most alluring and which, in his view, endowed Lagrange’s specific result with poetical dignity. For instance, it is well known that one conventional perception of poetry in the early 1800s ascribed to the poet the role of prophet or visionary, identifying and clarifying that which previously had only been vaguely sensed or dimly perceived.[30] In particular, poetry was often understood to illuminate those underlying commonalities of experience which, before the revelation of poetic insight, had only been imperfectly recognised and partially expressed. For example, in the 1802 Preface to the Lyrical Ballads, Wordsworth asserted that poetry was intended to inspire pleasure and that the mind often derives this from “ the perception of similitude in dissimilitude” (Wordsworth and Coleridge, 82). Clearly, in this respect, the role of the (applied) mathematician and the poet are analogous if not identical: both seek to reveal hidden patterns that unify diverse areas of experience. Most elementary definitions of science recognise that it seeks to reveal an underlying order in the pervasive, apparent incoherence of the natural world, and, presumably, it was this revelation of hidden coherence which, for Hamilton, was essentially poetical. Intriguingly, this central idea also appears to have its roots in a Coleridgean interpretation of scientific research. Writing in The Friend in 1818, Coleridge had discussed the nature of chemical research and had claimed that “the striving after unity of principle, through all diversity of forms [… was …] poetry, as it were, substantiated and realised” (Coleridge, 86). Seemingly, in the early 1800s, the perception of unity underlying apparent diversity was considered to constitute a poetical insight, and therefore it is not surprising that theorems in a mathematical treatise which manifested such insights should be classified as possessing sufficient “dignity” to enable the treatise in which they are embedded to be viewed as “a kind of scientific poem”.
V. Conclusion
In his 2005 monograph When Physics Became King, Iwan Morus argues convincingly that the modern conception of ‘physics’ as a distinct scientific sub-discipline emerged during the 1830s. As he notes,
Romantic science in the early nineteenth century was a loose collection of practices and ideas rather than a coherent school or system. […] In some respects, maybe, a philosophy that placed so much emphasis on the role of individual inspiration in the discovery of nature was not aimed in any case at producing a collective research program. Future generations of natural philosophers, particularly in the German lands, were scathing in their condemnation of the metaphysical excesses of their predecessors. Romanticism provided, however, some practical and intellectual tools for self-fashioning and disciplinary fashioning in the opening decades of the nineteenth century. In the face of massive social and intellectual upheaval at the turn of the century it helped to construct a new vision of nature as a unified, organic whole, which in turn provided a resource both for constructing new scientific disciplines – including physics – and for constructing a new image of the natural philosopher and his place in society.
Morus 2005, 63
“Metaphysical excesses” is certainly a phrase that could be used with reference to Hamilton, yet, as Morus indicates, these philosophical proclivities facilitated the emergence of new scientific sensibilities. As this article has shown, Hamilton was unquestionably one of the pioneering physicists of the 1830s, and yet his conviction that pure mathematics and physics were both, in part, poetical endeavors reveals the intricacy of his view. As discussed above, he explicitly stated on several occasions that he wished to “infuse into [his] scientific progress something of the spirit of poetry” (Graves I, 354), and while the belief that beauty and truth, as manifest in poetry and mathematics, existed in an analogical relationship to each other was in no way remarkable in the early nineteenth century, he sought more assiduously than many of his contemporaries to illuminate the precise nature of this association. More specifically, he explored the similarities between poetical and mathematical creation, emphasising both the comparable pleasure induced by the contemplation of poetical and mathematical objects, and the manner in which these complementary disciplines offer an escape from the dreary confinement for daily life. In addition, inspired partly by philosophical idealism, he stressed the comparable role of the creative imagination in poetical and mathematical composition. Most significantly, though, Hamilton’s belief in the association of poetry and mathematics caused him to concentrate specifically upon the aesthetic aspects of mathematics, viewing scientific treatises as quasi works of literature, and stressing repeatedly that the ‘poetry’ of axiomatic-deductive reasoning was manifest both in the formal beauty of the manner in which the method was deployed, and in the capacity of the results obtained to reveal hidden unity in apparent diversity. Indeed, Hamilton considered these qualities to be of such importance that, even in the realm of applied mathematics, he maintained that the formal beauty of a mathematical argument could still be appreciated even if the empirical predictions elicited from the theory were subsequently demonstrated to be inaccurate.
Hamilton’s belief in the inherent creativity of the human mind was perhaps most movingly expressed with reference to the poetical nature of scientific research in an extract from a lecture delivered in 1833. In this lecture, he considers a possible future in which science has managed to answer all questions concerning the natural world, and therefore it is one of the earliest examples of a teleological discussion apropos the end of science. In this lecture, he briefly depicts the seemingly barren intellectual landscape that would characterise such a state, but he then continues
[...] even then we may be sure that new desires would arise, the intellect would find something to do; though we knew all the parts, we should wish to know them more and more as a whole, to make the infinite one; we should desire to fuse them all and interpenetrate them all with mind, and throw over them all the poetry of Science; and from the seemingly finished work there would rise up a new and growing enterprise, an unexplored and unimagined world of genius.
71
Perhaps inevitably, the “poetry of Science” remains an ill-defined, elusive notion, but there is no doubt that throughout his life Hamilton attempted repeatedly to explore the interconnections that unify poetry and mathematics during the Romantic period, and possibly, in his finest creative scientific and literary work, he succeeded in revealing some of their shared qualities.
Appendices
Biographical Notice
Marcus Tomalin is a Fellow of Downing College and an Affiliated Lecturer in English at the University of Cambridge, UK. His research focuses upon the literature of the Romantic period, as well as missionary linguistics and the development of syntactic theory. His many publications include the monographs Linguistics and the Formal Sciences (2006) and Romanticism and Linguistic Theory (2008).
Notes
-
[1]
The most comprehensive recent biographies of Hamilton are Hankins 1980 and O’Donnell 1983.
-
[2]
Hamilton’s scientific papers were collected together in the four volumes of The Mathematical Papers of Sir William Rowan Hamilton that were published by Cambridge University Press (under various editors) from 1931-2000. Hamilton’s friendship with Wordsworth is briefly described in Hewitt 2005 where it is suggested that the former influenced the latter’s understanding of geometry.
-
[3]
For Hamilton’s letters, see Graves, Vol.1, 1882, (hereafter Graves I), 488ff and for Wordsworth’s response, see ibid., 491ff. It is perhaps unnecessary to state that the word ‘science’ inevitably provokes interpretative complexities, and it is important to recognise that, in the early nineteenth century, the term did not identify a particular, isolatable set of methodologies and procedures. For helpful remarks on the disunity of science during this period, see Cunningham and Jardine 1990, especially pp.1-9.
-
[4]
Once again, it is perhaps unnecessary to stress that, in the early 1800s, the word ‘art’ designated a wider range of cultural activities than it does today. As David Knight (for one) has emphasised repeatedly, “Around 1800 ‘science’ was not opposed to the ‘arts’; there was nothing like the “Two Cultures” of C.P. Snow’s famous essay. Indeed, the then current classification of subjects would have put engineering among the arts, a useful rather than a fine art, while almost all other subjects now taught in universities, such as chemistry, history and theology, would have been sciences” (Knight 1998, 48).
-
[5]
Hamilton’s account of their first meeting is detailed in Graves I, 261ff. Further information and discussion concerning Hamilton’s relationship with Wordsworth can be found scattered throughout Hankins 1980 and O’Donnell 1983.
-
[6]
For various insightful perspectives concerning Wordsworth’s knowledge of contemporaneous science, see Thomas and Ober 1989 and Wyatt 1995.
-
[7]
A good biography of Davy that includes numerous examples of his poetry is Knight 1992, while a more specific discussion of his verse can be found in Fullmer 1960. McNeil 1987 provides an authoritative biography of Erasmus Darwin.
-
[8]
A comprehensive discussion of truth and beauty in relation to Romantic verse can be found in Jamil 1989. Of course, many of these ideas have their roots in the conflux of aesthetics and rationality which occurred during the eighteenth century. For instance, in his monograph Knowledge and Indifference in English Romantic Prose (2003), Tim Milnes discusses the neoplatonist origins of Anthony Ashley-Cooper (the Third Earl of Shaftesbury)’s attempts to associate truth and beauty (esp. 31-33).
-
[9]
For a recent discussion of the problems associated with the term ‘literature’ during this period, see Fulford, Lee, and Kitson, 2-25.
-
[10]
For a detailed discussion of the range of meanings associated with the term ‘enthusiasm’ in the eighteenth and nineteenth centuries, see Mee 2003, especially pp.1-19.
-
[11]
Accessible but comprehensive introductions to the notion of infinity in mathematics can be found in Rucker 1995 and Moore 2001.
-
[12]
For example, see Tsur 1992.
-
[13]
For a consideration of Davy’s possible influence upon the prelude to Lyrical Ballads, see Sharrock 1962, xvii.
-
[14]
Francis Edgeworth’s letter, dated the 7th August 1829, can be found in Graves I, 337ff, and for Hamilton’s various replies, see Graves I, 346ff.
-
[15]
Although the phrases “pure mathematics” and “applied mathematics” did not become standard until the end of the nineteenth century, Hamilton consistently and explicitly adopted this distinction. For instance, in one of his 1832 lectures he contrasted “the physical and the purely mathematical sciences”, noting that “[t]hese purely mathematical sciences of algebra and geometry are sciences of the pure reason, deriving no weight and no assistance from experiment, and isolated, or at least isolable, from all outward and accidental phenomena” (Graves I, 642-643). In addition, later in the same lecture he observes that “the relations of the pure mathematics are relations between our own thoughts themselves; while the relations of mixed or applied mathematical science are relations between our thoughts and phenomena” (644).
-
[16]
Tuveson 1960 is still a insightful introduction to the vast subject. In this ambitious work, eighteenth-century perspectives on the nature of the imagination are discussed in relation to Adam Smith, John Locke, Thomas Hobbes, and many others. Other discussions can be found in contemporaneous sources, especially in the well-known prose writings of Wordsworth, Thomas Love Peacock, Percy Shelley, and Samuel Taylor Coleridge. For instance, the nature and function of the imagination is mentioned in Wordsworth’s prefaces to Lyrical Ballads, in Peacock’s The Four Ages of Poetry and Shelley’s A Defence of Poetry. An early consideration of Coleridge’s complex views concerning the imagination can be found in Baker 1957 and, more recent assessments include Gravil, Newlyn, and Roe 1985, and Barth and Mahoney 1990.
-
[17]
An excellent recent introduction to all aspects of German Idealism can be found in Ameriks 2000. The main debate in recent years has focused upon the extent to which the work of Kant, Fichte, and Schelling influenced the research of Davy, Faraday, and their contemporaries. For a glimpse of this important discussion, see Williams 1973, Levere 1981 (especially chapter 3), and Caneva 1997.
-
[18]
Graves R.P., Life of Sir William Rowan Hamilton, Vol. 2, (Dublin: Hodges Figgis, 1885), (hereafter Graves II), 87.
-
[19]
The influence of Kant upon Hamilton’s development of an algebra based on the notion of pure time has been exhaustively explored in Hankins 1976 and Hankins 1977, and Winterbourne 1982 (Vol.9. 195-200).
-
[20]
Hamilton met Coleridge “several times” in the spring of 1832. For his account of these meetings see Graves I, 540.
-
[21]
The relationship between Davy and Coleridge is discussed at length in Levere 1981. For detail information concerning Coleridge’s views about the creativity of scientific research see ibid., 20ff.
-
[22]
A detailed biography of Lagrange can be found in Herrmann 1963.
-
[23]
Hamilton is most likely to have used the 1811 revised edition of Mécanique analytique, nouvelle édition, (Paris: Ve Courcier, 1811) which Lagrange was preparing when he died. A useful recent English translation of this edition of Lagrange’s text can be found in Boissannade and Vagliente 2005. For reasons that do not concern us here, in most contemporary physics texts, ‘le Principe des Vitesses Virtuelle’ is now known as ‘The Principle of Virtual Work’.
-
[24]
The phrase ‘the Mathematician of Alexandria’ was an epithet that was traditionally used with reference to Euclid.
-
[25]
The inherent theatricality of mathematics is discussed in Curtin 1982, 26ff.
-
[26]
It is remarkable that a comparably dynamic theory of mathematical discovery was not formulated explicitly until the 1960s when Imre Lakatos adapted Karl Popper’s work concerning the nature of scientific discovery and applied it in a purely mathematical context. For specifics, see Lakatos 1976.
-
[27]
While it is not known which edition(s) of Euclid Hamilton had encountered by the time he wrote A Waking Dream in 1822, it is possible to establish which editions he was most likely to have studied. For instance, the fact that, by the age of 17, Hamilton had acquired a working knowledge of both Greek and Latin suggests that he would have been able to read Euclid in a Greek edition such as Gregory 1703, or Simson 1756. However, it is also likely that he would have encountered English translations such as Playfair 1795, though the numbers that Hamilton uses when referring to the definitions, postulates, and axioms correspond to the numbering in the Greek and Latin texts rather than to a text such as Playfair’s which presents a revised and re-numbered version of the foundations of Euclid’s treatise. For convenience, all quotations from Euclid used in the following discussion will be translated directly from the Greek text.
-
[28]
These definitions all concern themselves with particular properties of a circle. For instance, definition 15 reads as follows: “A circle is a flat shape [skema epipedon] encompassed by a single line such all straight lines falling within it from one point among those lying within the figure are equal to each other”.
-
[29]
Postulate 1 states that it is possible “to draw a straight line from any point to any point”, while postulate 3 states that it is possible “to draw a circle with any centre and distance [diastemati]”.
-
[30]
For a robust discussion of this complex topic, see Kugel 1990.
Works Cited
- Ameriks K. Ed. The Cambridge Companion to German Idealism. Cambridge: Cambridge University Press. 2000.
- Baker J. V. The Sacred River: Coleridge’s Theory of the Imagination. New York: Louisiana State University Press. 1957.
- Barth J. R. and Mahoney, J. L. Eds. Coleridge, Keats and the Imagination. Missouri: University of Missouri Press. 1990.
- Boissannade A. and Vagliente, V. N. Eds. Analytical Mechanics. London, Boston, Dordrecht: Kluwer Academic Publishers. 2005.
- Caneva K. L. “Physics and Naturphilosophie; A Reconnaissance”. History of Science. Vol. 35. Part 1. No. 107. 1997.
- Caudwell C. Illusion and Reality: A Study of the Sources of Poetry. London: Lawrence & Wishart. 1937.
- Coleridge S. T. The Friend. Rooke, B. E. Ed. Vol. 4. Princeton: Princeton University Press. 1969[1818].
- Cunningham A. and Jardine, N. Romanticism and the Sciences. Cambridge: Cambridge University Press. 1990.
- Curtin D.W. Ed. The Aesthetic Dimension of Science. New York: Philosophical Library. 1982.
- Davy H. Collected Works. Vol. 8. London: Smith, Elder and Co. 1840.
- De Morgan A. Sir W.R. Hamilton. Gentleman’s Magazine. Vol.1 (new series). 1866. 128-134.
- Fekete J. The Critical Twilight. London: Routledge and Kegan Paul. 1976.
- Fulford T, Lee D., and Kitson P. J. Literature, Science and Exploration in the Romantic Era: Bodies of Knowledge. Cambridge: Cambridge University Press. 2004.
- Fullmer J. “The Poetry of Humphry Davy”. Chymia, 6. 1960. 102-126.
- Giere R. N. and Westfall R. S. Eds. Foundations of Scientific Method: The 19th Century. London: Bloomington Press. 1973.
- Gill, S. C. William Wordsworth: A Life. Oxford: Clarendon Press. 1989.
- Graves R.P. Life of Sir William Rowan Hamilton. 2 Vols. Dublin: Hodges Figgis. 1882.
- Gravil R., Newlyn L., and Roe N. Eds. Coleridge’s Imagination. Cambridge: Cambridge University Press. 1985.
- Gregory D. Eukleidia Ta Soizomena. Oxford: Theatro Sheldonia. 1703.
- Hamilton W.R. A Preliminary and Elementary Essay On Algebra as the Science of Pure Time. Transactions of the Royal Irish Academy.Part I. Vol.17. 1837. 293-422.
- Hamilton W.R. On a General Method in Dynamics. Philosophical Transactions of the Royal Society. Part II. 1834. 247-308.
- Hamilton W.R. The Mathematical Papers of Sir William Rowan Hamilton. Cambridge: Cambridge University Press. 1931-2000.
- Hankins T. L. “Algebra as Pure Time: William Rowan Hamilton and the Foundations of Algebra”. In Machemar P. K. and Turnbull R. G. Eds. Motion and Time, Space and Matter. Ohio: Ohio University Press. 1976. 327-359.
- Hankins T.L. “Triplets and Triads: Sir William Rowan Hamilton on the Metaphysics of Mathematics”. Isis 68. 1977. 175-193.
- Hankins T.L. Sir William Rowan Hamilton. Baltimore: Johns Hopkins University Press. 1980.
- Hardy G.H. A Mathematician’s Apology. Cambridge: Cambridge University Press. 1940.
- Herrmann D. Joseph Louis Lagrange (1736-1813). Berlin: Treptow. 1963.
- Hewitt, R. ‘Wordsworth’s Irish Friend’. The Times Literary Supplement. September 30th , 2005. 14.
- Jackson, N. Science and Sensation in Romantic Poetry. Cambridge: Cambridge University Press. 2008.
- Jamil T. Transcendentalism in English Romantic Poetry. New York: Vantage Press. 1989.
- Kitson, P. Literature, Science and Exploration in the Romantic Era. Cambridge: Cambridge University Press. 2004.
- Knight D. M. Humphry Davy: Science and Power. London: Blackwell Press, Ashgate Variorum. 1992.
- Knight D. M. Science in the Romantic Era. London: Ashgate Variorum. 1998.
- Kugel J. L. Ed. Poetry and Prophecy: the Beginnings of a Literary Tradition. Ithaca: Cornell University Press. 1990.
- Lagrange J.L. Mécanique analytique, nouvelle edition. Paris: Ve Courcier. 1811.
- Lakatos I. Proofs and Refutations. Cambridge: Cambridge University Press. 1976.
- Levere T. H. Poetry Realised in Nature: Samuel Taylor Coleridge and Early Nineteenth Century Science. Cambridge: Cambridge University Press. 1981.
- McNeil M. Under the Banner of Science: Erasmus Darwin and his Age. Manchester: Manchester University Press. 1987.
- Machemar P.K. and Turnbull R.G. Eds. Motion and Time, Space and Matter. Ohio: Ohio University Press. 1976.
- Mee J. Romanticism, Enthusiasm, and Regulation: Poetics and the Policing of Culture in the Romantic Period. Oxford: Oxford University Press. 2003.
- Milnes, T. Knowledge and Indifference in English Romantic Prose. Cambridge: Cambridge University Press. 2003.
- Moore A. W. The Infinite. London and New York: Routledge. 2nd. Ed. 2001.
- Morus, I.R. When Physics Became King. Chicago: University of Chicago Press. 2005.
- Murray, L. English Grammar. York. 1795.
- O’Donnell S. William Rowan Hamilton: Portrait of a Prodigy. Dublin: Boole Press. 1983.
- Peacock T. L. The Four Ages of Poetry. Ed. Brett-Smith H.F.B. and Jones C.E. The Works of Thomas Love Peacock. London: Constable. 1926[1821]
- Playfair J. Elements of Geometry: containing the first six books of Euclid. Edinburgh: Bell & Bradfute; and G.G. & J. Robinson. 1795.
- Poggi, S. and Bossi, M. Romanticism in Science: Science in Europe, 1790-1840. Dordrecht and London: Kluwer Academic. 1994.
- Reiman D. H. and Fraistat N. Shelley’s Poetry and Prose. London: W.W. Norton & Company. 2002.
- Rucker R. Infinity and the Mind: The Science and Philosophy of the Infinite. Princeton: Princeton University Press. Reprinted 1995.
- Sharrock R. “The Chemist and the Poet: Sir Humphrey Davy and the Preface to the Lyrical Ballads”. Notes and Records of the Royal Society. 1962.
- Simson R. Euclidis Elementorum: Libri Priores Sex, Item Undecimus et Duodecimus. Glasgow. 1756.
- Simpson J and Weiner E. Oxford English Dictionary. 2nd Ed. Oxford: Oxford University Press. 1972-86.
- Tait P. G. Sir William Rowan Hamilton. North British Review 46. 1866. 37-74.
- Thomas W. K and Ober W. U. A Mind For Ever Voyaging: Wordsworth at Work Portraying Newton and Science. Edmonton: University of Alberta Press. 1989.
- Tsur R. Towards a Theory of Cognitive Poetics. London: North-Holland. 1992.
- Tuveson E. L. The Imagination as a Means of Grace: Locke and the Aesthetics of Romanticism. New York: Guardian Press. 1960.
- Watkins D. P. Keats’s Poetry and the Politics of the Imagination. London and Toronto: Associated University Presses. 1989.
- Williams L. P. “Kant, Naturphilosophen and Scientific Method”. In Giere and Westfall 1973.
- Winterbourne A. T. “Algebra and Pure Time: Hamilton’s affinity with Kant”. Historia Mathematica. 1982.
- Wordsworth W. The Prelude. Ed., De Selincourt E. and Gill S. Oxford: Oxford University Press. 1990[1805].
- Wordsworth W. and Coleridge S.T. Lyrical Ballads. Ed. Mason M. Longman Press. 1992[1802].
- Wyatt J. Wordsworth and the Geologists. Cambridge: Cambridge University Press. 1995.


