Étude des pratiques évaluatives en mathématiques de 25 professeurs des écoles français : une approche didactique à partir de l’analyse des tâches données en évaluation

Sayac, Nathalie

doi:https://doi.org/10.7202/1043566ar

Introduction

En France, depuis peu, l’évaluation des élèves est devenue une question vive qui préoccupe les différents acteurs de l’éducation jusqu’au plus haut niveau de l’institution scolaire. Cet intérêt spécifique s’est traduit sur plusieurs plans. Tout d’abord, à travers la Loi d’orientation et de programmation pour la refondation de l’École de la République du 8 juillet 2013, qui a introduit de nouvelles prescriptions institutionnelles sur l’évaluation et mis l’accent sur « l’évaluation positive », « valorisant les progrès » et évitant ainsi la « notation sanction ». Elle insiste d’ailleurs sur le caractère simple et lisible par les familles de l’évaluation positive pour mesurer le degré des connaissances, des compétences et la progression des élèves. Puis, à travers la création d’un Conseil national d’évaluation du système scolaire (CNESCO) en 2013 et à travers la publication de diverses prescriptions ciblant des questions d’évaluation (nouveaux programmes en 2016, nouveau référentiel de compétences professionnelles, circulaires de rentrée, etc.). La pression institutionnelle est donc devenue plus forte sur cette activité que les enseignants français pratiquent au quotidien dans leur classe. Ce qui est moins clair est la manière dont ils évaluent réellement les apprentissages de leurs élèves. Un rapport produit en juillet 2013 par l’Inspection générale de l’éducation nationale (IGEN) a établi que :

Le constat d’une absence d’objectivité est quasi constant : on ne sait pas ce qu’on évalue, les niveaux de performance ne sont pas définis [...]. L’absence de différenciation entre évaluation formative et sommative est récurrente. Le mélange des deux empêche les enseignants de connaître le niveau des acquis des élèves et donne aux élèves le sentiment d’être en contrôle permanent, ce qui engendre une forme de « stress » pour certains
IGEN, 2013, p. 31

L’enquête TALIS[1] (DEPP, 2013 ; OCDE, 2014) a également pointé quelques caractéristiques françaises autour de l’évaluation des élèves. Elle a notamment témoigné du fait que plus de 90 % des professeurs français avaient des pratiques d’évaluation très variées et que 86 % d’entre eux concevaient leurs propres évaluations (alors que la moyenne des pays se situe à 68 %).

Néanmoins, Mons précise, dans l’introduction du rapport de 2014 du CNESCO sur l’évaluation des élèves par les enseignants dans la classe, que ce type d’évaluation est peu étudié :

Les évaluations internes par les enseignants dans la classe, bien qu’au coeur historiquement de l’institution scolaire, et analysées, à travers différents champs scientifiques [...], par des chercheurs s’intéressant à la pédagogie (en particulier aux effets des évaluations sur les apprentissages des élèves), ont suscité peu d’état des lieux des pratiques des enseignants dans leurs classes
CNESCO, 2014, p. 7

Pour aller au-delà de ces constats établis à partir d’enquêtes quantitatives, nous avons donc voulu explorer cette problématique de l’évaluation des élèves en classe en étudiant, plus précisément, les pratiques d’évaluation en mathématiques des professeurs des écoles[2], en France. À cette fin, nous avons conçu une recherche qualitative visant à les étudier, dans la réalité du terrain, sur un domaine spécifique nous permettant de prendre en compte les différentes années de l’école élémentaire[3], soit du CP au CM2. Nous avons ainsi convenu de travailler sur le domaine de la numération des nombres entiers.

Cette recherche s’inscrit dans le cadre d’une approche didactique de l’évaluation que nous souhaitons développer et qui appréhende les pratiques évaluatives en mathématiques des enseignants dans la continuité des travaux sur leurs pratiques plus générales, notamment ceux de la « double approche » (Robert & Rogalski, 2002), dont nous retenons les dimensions centrales de stabilité et de complexité, et ceux de Roditi (2011), qui considère l’évaluation comme une des activités organisatrices des pratiques enseignantes.

Dans notre recherche, nous nous sommes principalement intéressée aux tâches mathématiques proposées en évaluation. Nous les avons analysées à l’aide d’un outil spécifique intégrant différents travaux en didactique des mathématiques et permettant de caractériser leur niveau de complexité (Sayac & Grapin, 2014, 2015). Nous avons également cherché à étudier et à comprendre comment les professeurs des écoles concevaient leurs évaluations et notaient les productions de leurs élèves, mais nous n’en rendrons pas compte dans cet article.

Nous avons choisi de montrer ici comment une analyse didactique des tâches évaluatives proposées par des professeurs des écoles permet à la fois de décrire du point de vue de la didactique des pratiques d’évaluation et de rendre compte des évaluations auxquelles sont soumis les élèves de l’école élémentaire française en mathématiques. L’étude des tâches proposées en évaluation nous permet en effet de mieux comprendre ce qui se joue sur le plan des apprentissages mathématiques des élèves, par la confrontation des savoirs enseignés avec les savoirs évalués.

Contexte

Chevallard et Feldmann (1986) ont été les premiers didacticiens des mathématiques à évoquer la question de l’évaluation dans leurs écrits, même s’ils se sont principalement intéressés à l’usage de la notation comme outil de négociation entre le professeur et ses élèves. Ils ont indiqué qu’une évaluation était « un acte par lequel, à propos d’un évènement, d’un individu ou d’un objet, on émet un jugement en se référant à un (ou plusieurs) critère(s), quels que soient ces critères et l’objet du jugement » (Chevallard & Feldmann, 1986, p. 4).

Dans leur Dictionnaire des concepts fondamentaux des didactiques, Cohen-Azria, Daunay, Delcambre, Lahanier-Reuter et Reuter (2013) ont précisé qu’étudier l’évaluation avec une approche didactique supposait de prendre en compte les relations entre enseignement, apprentissages et contenus, entre évaluation et construction des disciplines scolaires ou encore entre didactiques et pédagogies. Ces relations nous semblent en effet fondamentales pour étudier les pratiques évaluatives des professeurs des écoles en mathématiques du point de vue de la didactique. Nous avons choisi, pour notre étude, de cibler plus spécifiquement les tâches mathématiques proposées par des professeurs des écoles en évaluation et de les mettre au regard de celles proposées durant la séquence dans laquelle l’évaluation s’inscrit.

Nous présentons ci-dessous quelques éléments théoriques relatifs à l’analyse des tâches mathématiques proposées en évaluation. Nous décrirons ensuite comment l’utilisation d’un outil développé dans le cadre d’une recherche antérieure appliqué à des tâches évaluatives proposées en mathématiques dans des classes de l’école élémentaire permet de produire des résultats pour les pratiques d’évaluation d’un échantillon de professeurs des écoles français.

Description de l’outil d’analyse

L’outil que nous utilisons (Sayac & Grapin, 2014, 2015) pour analyser les tâches évaluatives proposées en évaluation s’inscrit dans la lignée des approches épistémo-didactique (Grugeon-Allys & Grapin, 2015) et psycho-didactique (Vantourout & Goasdoué, 2014). Il a été conçu pour analyser des évaluations externes, mais nous pensons qu’il reste pertinent pour étudier les tâches proposées lors d’évaluations internes. Nous souhaitons donc éprouver son usage dans ce cadre. Ayant été conçu pour analyser des items visant à évaluer à la fois les connaissances et les compétences des élèves, il intègre ces deux dimensions et se décline en trois facteurs : deux facteurs de complexité relatifs aux connaissances (FC1 et FC2) et un facteur de compétence (NC). Ces facteurs comprennent chacun trois niveaux correspondant à des degrés de difficulté croissants.

Avant de présenter ces facteurs, il convient d’abord de préciser qu’ils ont été conçus pour porter une attention particulière aux entrées qui les définissent (compréhension de la tâche, savoirs mathématiques, compétences), et non pour poser un verdict indiscutable sur le niveau de complexité des tâches étudiées. Nous avons qualifié ces facteurs de « facteurs de complexité » en référence aux travaux de Gras (1977), repris par Bodin (2004) sur les taxonomies des énoncés de problèmes mathématiques permettant de classer l’activité des élèves selon des niveaux hiérarchisés de complexité cognitive. Les trois niveaux permettant de déterminer la complexité a priori[4] des tâches prennent en compte les années d’études, c’est-à-dire que des niveaux de complexité différents peuvent être attribués à une même tâche selon l’année d’études dans laquelle la tâche a été donnée[5].

Facteur de complexité 1 (FC1) : la compréhension de la tâche

Le niveau de langue de l’énoncé, la nature et la quantité d’informations à traiter par l’élève ainsi que la présence d’un exemple sont pris en compte pour déterminer le premier niveau de complexité de la tâche. Ce qui importe dans ce facteur, c’est de considérer comment l’élève est amené à comprendre, aisément ou de façon plus implicite, la tâche qu’il doit réaliser.

L’exemple ci-dessous (voir Figure 1), extrait d’une évaluation proposée en CP, illustre bien le fait que certaines consignes ne sont pas toujours très claires. Par conséquent, elles conduisent à une compréhension de la tâche à réaliser moins explicite pour l’élève, ce qui se traduit par un facteur de complexité 1 élevé (de niveau 2, voire 3) :

Figure 1

***Exercice donné en CP par un professeur de notre échantillon***

En effet, même si la tâche de coloriage est explicite, celle de repérage de la boule à colorier l’est beaucoup moins. L’élève doit comprendre, sans aucune indication supplémentaire, qu’il doit d’abord situer la boule du 83 entre les boules des 70, 80 et 90 présentées, avant de la colorier dans la couleur indiquée.

Facteur de complexité 2 (FC2) : les savoirs mathématiques en jeu

Ce facteur est directement lié aux savoirs mathématiques en jeu. De ce point de vue, la tâche à réaliser peut être plus ou moins complexe. Nous nous référons aux divers travaux effectués en didactique des mathématiques dans les différents domaines concernés par l’évaluation pour déterminer la complexité des tâches mathématiques relativement à ce facteur et au domaine considéré (Chambris, 2008 ; Mounier, 2010 ; Tempier, 2013 ; Perrin-Glorian, 2012).

Par exemple, la tâche de comparaison de deux nombres entiers peut s’avérer plus ou moins complexe en jouant sur différentes variables didactiques (taille et présentation des nombres, présence de zéros). Voici une illustration des différents niveaux de ce facteur autour de cette tâche, issue de différentes évaluations récoltées durant notre étude :

Niveau 1 : Avec 23 456 et 23 537, le nombre de chiffres constituant ces nombres est le même. L’élève a simplement à appliquer la règle de comparaison étudiée en classe.
Niveau 2 : Avec 30 101 019 et 30 090 109, les zéros présents dans les deux nombres augmentent la complexité de la tâche, même si l’élève a certainement déjà réalisé ce type de comparaison.
Niveau 3 : Avec 301 011 190 et 300 000 + 11 000 + 200, ces nombres ne sont pas présentés de la même façon. L’élève doit recomposer le second nombre avant de pouvoir effectuer la comparaison demandée. La tâche de comparaison est donc ici rendue plus complexe.

Facteur de compétence (NC)

Il ne s’agit pas, pour ce facteur de compétence, de discuter de la pertinence de l’évaluation par compétences ni de la difficulté à la réaliser (Dierendonck & Fagnant, 2014 ; Demonty, Fagnant & Dupont, 2015), mais de déterminer des niveaux de compétence permettant de prendre en compte cette dimension dans l’analyse des tâches. Notre définition de compétence s’inspire de celle de Perrenoud (1997), mais prend également en compte l’aspect inédit de la tâche à réaliser retenu par certains auteurs (Beckers, 2002 ; Rey, Carette & Kahn, 2002). Il nous semble que ce caractère est déterminant pour témoigner de la disponibilité des connaissances que les élèves mobilisent lorsqu’ils réalisent une tâche mathématique. Nous appréhendons cette disponibilité à travers les différents niveaux de mise en fonctionnement des connaissances (Robert & Rogalski, 2002). Pour nous, une compétence se définit donc comme « une capacité d’agir de manière opérationnelle face à une tâche mathématique qui peut s’avérer inédite, en s’appuyant sur des connaissances que l’élève mobilise de façon autonome » (Sayac & Grapin, 2015, p. 113).

Nous avons donc défini trois niveaux de compétence, que nous illustrons à travers la tâche de mise en correspondance entre une surface à hachurer et une fraction :

Cette tâche relève d’un bas niveau de compétence puisque l’élève doit simplement appliquer ses connaissances pour réaliser une tâche extrêmement usuelle pour lui.

L’élève doit cette fois prendre à sa charge le découpage en quatre parties égales du carré, mais la figure proposée le permet aisément. Il a pu déjà réaliser ce type de tâche auparavant.

Cette fois, l’élève se trouve devant une tâche relevant d’un haut niveau de compétence puisqu’il doit d’abord réaliser que la fraction 5/10 est égale à la fraction ½ avant de pouvoir hachurer les quatre carreaux correspondant à la moitié du rectangle. Pour réaliser cette tâche, l’élève n’est en rien guidé dans sa démarche et n’a certainement jamais réalisé ce type de tâche.

Nous avons choisi ces exemples pour illustrer les différents niveaux de compétence de notre outil, mais nous aurions également pu les utiliser pour illustrer les différents niveaux de complexité du facteur 2[6]. En effet, différents travaux en didactique des mathématiques autour de la notion de fraction (Brousseau, 1989 ; Duval, 1993 ; Sensevy, 1996 ; Adjiage, 2001 ; Gagatsis, Elia & Mougi, 2002) nous amènent à distinguer les niveaux de complexité de ces tâches, également croissants[7].

Cet outil permet donc de déterminer la complexité a priori d’une tâche mathématique à partir de l’attribution de niveaux relatifs aux trois facteurs qui le composent. Ainsi, les niveaux de complexité 3 pour le premier facteur (FC1⇒3), 2 pour le deuxième (FC2⇒2) et 3 pour le facteur de compétence (NC⇒3) ont été attribués à la tâche suivante (voir Figure 2), proposée à des élèves de CM2 :

Figure 2

***Exercice donné en évaluation en CM2 par un professeur de notre échantillon***

Nous considérons que cette tâche est très complexe du point de vue du premier facteur (niveau 3) en raison de la longueur de l’énoncé, de la multiplicité des consignes données et des mots ou expressions utilisés. En effet, du point de vue du lexique, l’expression « de proche en proche » et l’emploi de deux mots (« trait » et « itinéraire ») pour désigner un même objet rendent complexe la compréhension de la tâche à réaliser par l’élève. Du point de vue des mathématiques, les nombres proposés ont des parties décimales de longueurs variables, ce qui génère une certaine complexité (niveau 2), sans toutefois qu’elle soit la plus élevée au regard de l’année d’études où cette tâche a été proposée. Concernant le niveau de compétence, nous avons également attribué le plus haut niveau (niveau 3), car, au-delà du nombre élevé de comparaisons à effectuer, l’élève doit gérer la disposition des nombres proposés dans l’espace alloué, ce qui surcharge la tâche à réaliser.

Méthodologie

Nous avons conçu une recherche en collaboration avec des professionnels de terrain intéressés par la question de l’évaluation en mathématiques. Pour constituer l’équipe de recherche, nous avons sollicité des formateurs de terrain investis dans la formation des professeurs des écoles : trois conseillers pédagogiques, deux maîtres formateurs et deux directeurs d’école élémentaire. Ces collègues ont facilité la récolte des données par leur implantation locale et ont participé à l’attribution, pour chacun des facteurs, des différents niveaux de complexité des tâches évaluatives proposées par les professeurs de notre échantillon.

Pour nous permettre d’étudier les pratiques évaluatives des professeurs des écoles, 25 professeurs ont accepté de nous fournir des données de natures différentes, avec des finalités complémentaires :

Un court questionnaire a permis de récolter des données biographiques et professionnelles des professeurs, indispensables pour examiner la dimension personnelle de leurs pratiques évaluatives ;
La ou les évaluations données par le professeur autour d’une séquence de numération ont permis d’étudier les différentes tâches les constituant ;
Les exercices donnés en classe ou en devoirs au cours de la séquence ont été récupérés. Il nous a en effet semblé indispensable d’explorer les questions de continuité et de rupture entre les tâches proposées lors de la séquence d’apprentissage et des évaluations ;
Un entretien semi-directif a été conduit auprès de chaque professeur visant à clarifier d’éventuels questionnements issus de l’analyse des tâches préalablement réalisée.

Parmi ces 25 professeurs se trouvent 9 enseignants du cycle 2 (CP et CE1) et 16 enseignants du cycle 3 (CE2, CM1 et CM2). Aussi, 8 enseignants sont dans des écoles classées en REP (Réseau d’éducation prioritaire), tandis que 3 sont dans des écoles rurales. Il y a 3 hommes et 22 femmes, dont 9 ont plus de 10 ans d’ancienneté (de 11 à 25 ans).

La totalité des évaluations récoltées s’est révélée être des évaluations sommatives. Nous avons donc étudié les 971 tâches données dans les 31 évaluations récoltées (comprenant de 16 à 82 tâches chacune) afin de déterminer leurs niveaux de complexité et de compétence. Nous avons également mis les tâches données en évaluation en regard avec celles données durant la séquence afin de repérer d’éventuels écarts entre elles. À partir de cette analyse, nous avons déterminé des questions susceptibles d’être posées pendant l’entretien visant à nous permettre de mieux comprendre le choix des tâches données et, éventuellement, de revenir sur des points spécifiquement repérés. Chaque entretien a été retranscrit et les réponses des professeurs ont été codées suivant une grille permettant de relever des éléments de pratique qui nous ont semblé incontournables : À quel moment élaboraient-ils leurs évaluations (en amont ou en aval de la conception de la séquence) ? Quelles ressources utilisaient-ils (sites Internet, manuels de la classe ou autres, programmes) ? Collaboraient-ils avec d’autres professeurs ou bien les élaboraient-ils seuls ? Quelle place accordaient-ils aux compétences des programmes ? Quelle notation adoptaient-ils (note chiffrée, lettres, niveaux d’acquisition de compétences) ? Quels usages faisaient-ils des évaluations (correction collective ou individuelle, identification de groupes d’élèves ayant des besoins spécifiques) ?

Nous avons réalisé des statistiques descriptives pour dégager des résultats, à la fois simples (par facteur) et combinés (en croisant les facteurs). La taille de notre échantillon et le nombre élevé de variables considérées ont rendu difficile toute autre exploitation[8].

Résultats

Conception des évaluations

Les professeurs de notre échantillon élaborent majoritairement seuls (72 %) les évaluations qu’ils proposent à leurs élèves, à partir de ressources qu’ils vont chercher sur Internet (72 %) ou à partir du manuel de la classe (68 %) ou d’autres manuels (68 %). Il semblerait qu’ils « piochent » ici ou là des exercices qu’ils assemblent pour élaborer des évaluations qui leur sont propres, et qui dépendent à la fois de ce qui a été fait durant la séquence[9] et de leurs attentes institutionnelles et professionnelles. Par ailleurs, près de la moitié des professeurs élaborent leurs évaluations en fin de séquence, au moment où ils estiment que leurs élèves sont « prêts à être évalués ». Si 36 % d’entre eux les élaborent en amont de la séquence, un certain nombre ont exprimé le fait qu’ils réalisaient des ajustements en fin de séquence. Concevoir une évaluation relève d’un travail personnel pour près des trois quarts des répondants de notre échantillon, ce qui pourrait expliquer la disparité constatée des tâches évaluatives proposées. Le lien avec le livret personnel de compétences (LPC)[10] des élèves, vecteur de communication entre parents et professeur, a été évoqué spontanément par 28 % des répondants lors de l’entretien qu’ils nous ont accordé. Pour ces professeurs, mais certainement pour d’autres qui ne l’ont pas exprimé spontanément[11], les évaluations sont conçues principalement dans le but de remplir le LPC. D’ailleurs, 64 % des répondants disent concevoir leurs évaluations à partir des compétences prescrites dans les programmes.

Analyse des évaluations

Dans l’ensemble, les tâches mathématiques proposées en évaluation à l’école élémentaire sont d’un niveau de complexité assez bas, aussi bien pour le facteur 1 que pour le facteur 2. Les professeurs des écoles ne veulent pas mettre en échec leurs élèves et attendent souvent, comme ils sont nombreux à nous l’avoir dit lors de leur entretien, que la majorité des élèves aient compris la leçon pour faire l’évaluation qu’ils ont prévue.

Le tableau 1 ci-dessous synthétise les pourcentages de tâches correspondant aux différents niveaux de nos facteurs :

Tableau 1

Répartition des pourcentages relatifs aux 971 tâches évaluatives par facteur et par niveau

-> See the list of tables

Concernant le facteur relatif à la compréhension de la tâche (FC1)

Pour nous permettre d’avoir une vision globale de la répartition des différents niveaux du facteur de complexité 1, nous avons dressé, pour chaque professeur, les pourcentages correspondant à l’ensemble des tâches qu’ils avaient données en évaluation et synthétisé les résultats dans la figure 3.

Figure 3

***Répartition des tâches données en évaluation par les 25 professeurs selon les 3 niveaux de complexité du facteur de complexité 1 (FCl)***

En ce qui concerne ce facteur de complexité, nous notons que la majorité des tâches d’évaluation proposées aux élèves ne relèvent pas d’un niveau élevé puisque les trois quarts d’entre elles sont du niveau 1 et que seules 2,7 % sont du niveau 3. Ce résultat est rassurant, dans la mesure où, pour évaluer les connaissances des élèves, il est important que ces derniers comprennent bien ce qu’ils doivent faire et que la complexité ne se situe pas dans la consigne ni dans la présentation de la tâche. Les tâches du niveau 3 sont souvent des tâches où ce que le professeur demande à l’élève de faire n’est pas explicite et où il revient à ce dernier de comprendre ce qui est attendu de lui avant de s’engager dans la résolution des tâches.

L’exemple ci-dessous (voir Figure 4), extrait d’une évaluation donnée en CE2, illustre bien le fait qu’une consigne peu claire peut conduire l’élève à mal interpréter ce qu’il doit faire :

Figure 4

***Réponse d’un élève de CE2 à une tâche incomprise***

Dans cet exemple, l’élève a mal lu ou mal interprété la consigne, qui, de fait, n’était pas très explicite. Nous avons pu constater que, souvent, lorsque les professeurs des écoles proposent une décomposition de nombres, ils accompagnent leur consigne d’une illustration, ce qui n’est pas le cas dans notre exemple. La présence ou non d’exemple est un des éléments que nous prenons en compte pour déterminer le niveau de complexité de ce facteur.

Pour estimer ce niveau de complexité, nous avons veillé à comparer les tâches travaillées durant la séquence avec les tâches évaluatives proposées en fin de séquence. En effet, certaines consignes auraient pu nous apparaître comme relevant d’un niveau de complexité élevé, alors qu’elles ne l’étaient pas forcément si, durant la séquence, les élèves s’étaient déjà retrouvés devant ce type de consigne, qui avait donc été explicitée à ce moment. Les niveaux de complexité de ce facteur ont intégré ce paramètre. La grande majorité des professeurs ont indiqué donner à leurs élèves, très strictement, les mêmes tâches que celles travaillées durant la séquence, certains le soulignant avec conviction. C’est d’ailleurs ce que nous avons constaté en confrontant les deux types de données.

Par ailleurs, durant les entretiens, de nombreux professeurs ont indiqué lire les consignes à haute voix et s’assurer que tous les élèves avaient compris ce qu’ils avaient à faire.

Comme le démontre le tableau 2, la répartition des niveaux de complexité relativement au facteur de complexité 1 (FC1) est assez homogène pour les deux cycles de l’école élémentaire.

Tableau 2

***Répartition des tâches par niveau et par cycle pour le facteur de complexité 1 (FC1)***

Nous pouvons donc retenir de cette enquête que les évaluations données à l’école élémentaire sont d’un niveau de complexité faible du point de vue des consignes et que les professeurs, quel que soit leur cycle d’enseignement, sont soucieux de ne pas proposer à leurs élèves des tâches qu’ils ne seraient pas à même de comprendre.

Concernant le facteur relatif aux savoirs mathématiques (FC2)

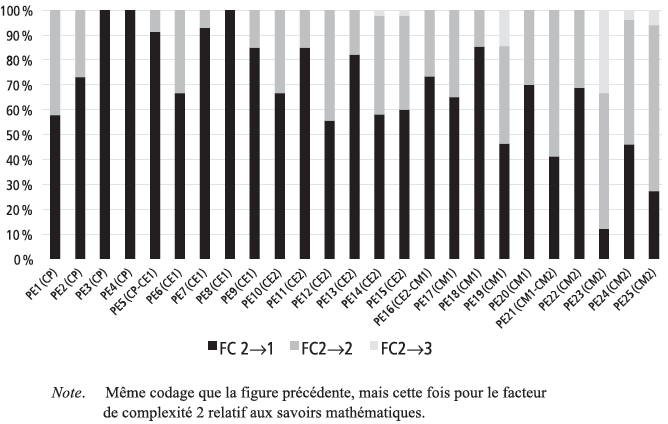
Sur le plan de la complexité des tâches mathématiques liée aux connaissances en jeu, nous avons également constaté que le niveau global des tâches demandées en évaluation à l’école élémentaire n’était pas très élevé : un peu plus des deux tiers des tâches relèvent du niveau le plus bas, environ 30 % se situent au niveau intermédiaire et seulement 2,5 % des tâches relèvent du niveau le plus haut et concernent exclusivement le cycle 3 (voir Figure 5). Le fait que peu de tâches évaluatives relevant d’un niveau de complexité élevé de ce facteur aient été proposées par les professeurs ne nous étonne guère, dans la mesure où la grande majorité des professeurs ont clairement affirmé qu’il ne s’agissait en aucun cas, lors des évaluations, de « mettre en échec » leurs élèves et que la « bienveillance » institutionnellement préconisée était de mise lorsqu’ils élaboraient leurs évaluations.

Figure 5

***Répartition des tâches données en évaluation par les 25 professeurs selon les 3 niveaux de complexité du facteur de complexité 2 (FC2)***

Sur le plan de la nature des tâches, la présence de zéros ou l’absence de certaines unités, la taille des nombres et le passage à l’unité supérieure ou inférieure sont les éléments principaux de complexification.

Parmi les tâches les plus complexes, du point de vue de ce facteur, nous avons relevé les tâches demandant à l’élève d’encadrer un nombre à un ordre d’unité près (p. ex., « Encadre ces nombres au millier près ») ou bien des correspondances de nombres en unités de numération présentées dans un ordre non hiérarchique (p. ex., « Écris en chiffre 7u de m + 3d + 1u + 5d de m »[12] en CE2).

En distinguant le niveau des tâches par cycle d’enseignement, nous constatons de toute évidence (voir Tableau 3) que les professeurs du cycle 3 proposent davantage de tâches de FC2 d’un niveau plus élevé.

Tableau 3

***Répartition des tâches par niveau et par cycle pour le facteur de complexité 2 (FC2)***

Il semblerait que la bienveillance revendiquée par les professeurs se heurte, au cycle 3, à la volonté de préparer les élèves à l’entrée au collège, ce qui se traduit, pour de nombreux professeurs, par la contrainte de donner des tâches plus complexes du point de vue des connaissances mathématiques, comme certains nous l’ont indiqué lors de l’entretien.

Le niveau de complexité des tâches données en évaluation varierait donc suivant le cycle d’apprentissage considéré. Le cycle 3 comporte davantage de tâches complexes, principalement en raison de la présence de zéros, de la taille des nombres et de l’identification des classes d’unité.

Concernant le facteur de compétence (NC)

Pour évaluer le niveau de compétence des tâches proposées en évaluation, nous n’avons pas retenu leur caractère innovant, dans la mesure où, pour tous les professeurs, les tâches données en évaluation ont été travaillées durant la séquence. Dans l’ensemble des évaluations récoltées, aucune tâche nouvelle n’a été donnée. Le caractère inédit des tâches, que certains associent à la notion de compétence comme le soulignent Rey, Carette et Kahn (2002), n’a donc pas été pris en compte pour ce facteur, ce qui a nécessité une adaptation de notre outil, qui l’intégrait initialement (voir Figure 6).

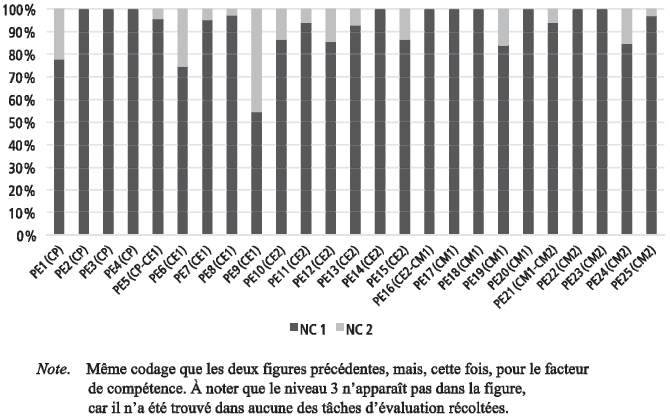
Pour différencier les niveaux de compétence, nous avons distingué les tâches qui nécessitaient la mise en relation de plusieurs connaissances ou savoir-faire des tâches qui étaient de simples applications de connaissances. Aucune tâche de niveau de compétence 3 (NC⇒3) n’a été donnée en évaluation, ce qui valide les propos des professeurs qui ont exprimé leur souci de ne pas mettre leurs élèves en échec. Toutefois, cela remet en question le contenu même de ces évaluations internes et leur finalité.

Figure 6

***Répartition des tâches données en évaluation par les 25 professeurs de l’échantillon selon les 2 niveaux de compétence (NC)***

Dans l’ensemble, le niveau de compétence 1 (NC⇒1) est celui retenu pour 92,6 % des tâches. Seulement 7,4 % des tâches données relèvent du niveau de compétence 2 (NC⇒2). En nous intéressant à l’année d’études où sont données les tâches de NC⇒2, nous constatons une grande variabilité qui laisse penser que cela ne semble pas rattaché à une année d’études ni à un cycle particulier, mais plutôt à la composante personnelle des professeurs.

Pour illustrer la différenciation des niveaux de compétence relativement à une même tâche, il nous semble pertinent d’évoquer les tâches de rangement de nombres proposées du CP au CM2. Au-delà des connaissances mathématiques nécessaires à la comparaison des nombres, le nombre de nombres à ranger est un élément important à considérer quant aux compétences requises pour réaliser la tâche. Si le professeur demande à l’élève de ranger cinq nombres, celui-ci doit réaliser un certain nombre de comparaisons deux à deux qui dépendent des nombres proposés, mais ce nombre grandit conséquemment si l’élève doit ranger neuf nombres. Les professeurs qui proposent un grand nombre de nombres à ranger souhaitent volontairement, pour la plupart, éprouver les connaissances de leurs élèves dans une situation plus complexe. Or, ils n’ont pas forcément conscience du fait que la complexité ne repose pas seulement sur les connaissances mathématiques qu’ils veulent évaluer, mais aussi sur des compétences méthodologiques. Nous avons choisi de prendre en compte ce type de difficulté pour ce facteur et donc en termes de compétence, bien que, dans l’approche psycho-didactique développée par Vantourout et Goasdoué (2014), il s’inscrit dans le second axe de la validité psycho- didactique, plus lié aux champs de la psychologie cognitive et de l’ergonomie. Ce choix résulte de la construction même de l’outil que nous avons développé et qui devait coïncider avec les finalités de l’évaluation externe étudiée[13]. Ce qui nous semble néanmoins important, c’est que ce type de complexité est pris en compte d’une façon ou d’une autre dans l’étude de tâches évaluatives, en complément d’une analyse strictement didactique.

Nous nous sommes également demandé si une distinction par cycle d’enseignement pouvait advenir concernant ce facteur.

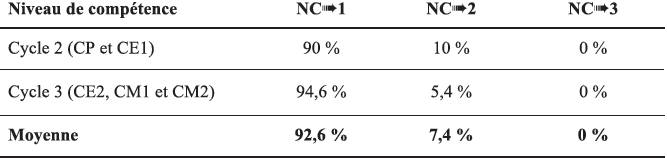
Tableau 4

***Répartition des tâches par niveau et par cycle pour le facteur de compétence (NC)***

Le tableau 4 témoigne du fait que, quel que soit le cycle, le niveau de compétence des tâches mathématiques données en évaluation à l’école élémentaire est extrêmement bas. Il convient donc de s’interroger sur la façon dont les professeurs conçoivent l’évaluation des compétences de leurs élèves en mathématiques au regard de la réduction de ces dernières à de simples applications directes de connaissances.

Variabilité des pratiques évaluatives

Afin d’affiner notre analyse, nous avons cherché à savoir si des résultats complémentaires pouvaient se dégager en croisant les facteurs et leurs différents niveaux de complexité. Nous avons donc calculé les moyennes pondérées[14] pour chaque professeur selon les trois facteurs, en fonction de la répartition par niveau de complexité des tâches proposées en évaluation (voir Tableau 5 en annexe).

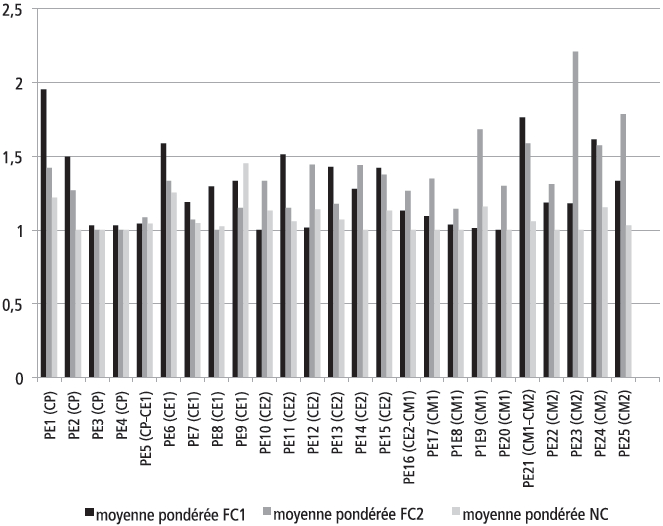
Figure 7

***Répartition de la moyenne pondérée des 3 facteurs par professeur***

La figure 7 obtenue ne permet pas vraiment de dégager des tendances, si ce n’est pour trois professeurs de CP qui ont des moyennes pondérées équilibrées pour les trois facteurs. Cela n’est toutefois pas suffisant pour en déduire que les professeurs de cette année d’études proposent à leurs élèves des tâches équilibrées du point de vue des trois entrées considérées. Néanmoins, sans que cela puisse vraiment être interprété comme des résultats fiables compte tenu du faible effectif de notre échantillon, il semblerait que la complexité des tâches relevant du FC1 soit souvent plus élevée pour les professeurs du cycle 2 que pour les professeurs du cycle 3, alors que, pour ces derniers, c’est plutôt la complexité des tâches relative au FC2 qui surpasse les deux autres. Il était déjà apparu que les tâches évaluatives proposées au cycle 3 étaient en moyenne plus complexes du point de vue des mathématiques en jeu que celles du cycle 2. Toutefois, que ces dernières soient plus complexes du point de vue de la consigne est assez étonnant et peu compréhensible. Il se pourrait néanmoins que les professeurs de CP et de CE1 n’aient pas toujours forcément conscience de la complexité liée aux énoncés ou aux consignes qu’ils proposent à leurs élèves. À moins que notre catégorisation par niveau pour ce facteur n’ait été trop sévère.

Nous retenons de ce croisement des trois facteurs par professeur qu’aucune tendance réelle ne se dessine et que les professeurs font des choix de tâches évaluatives très personnels, dont la complexité peut reposer sur une ou plusieurs des entrées que nous avons considérées pour rendre compte de la complexité des tâches mathématiques. Cela rejoint les travaux de Cizek, Fitzgerald et Rachor (1996), qui ont montré que les pratiques d’évaluation des professeurs étaient très variables et imprédictibles, car dépendantes de trop nombreux paramètres personnels et contextuels.

Il s’avère donc que l’analyse des tâches mathématiques réalisée à l’aide de nos facteurs de complexité et de compétence n’a pas permis de dégager des caractéristiques partagées suivant les années d’études où les professeurs de notre échantillon enseignent. Les autres données récoltées lors de cette étude nous permettent néanmoins de produire quelques résultats complémentaires, notamment du côté de la conception des évaluations.

Discussion

L’outil que nous avons utilisé pour étudier les tâches mathématiques données dans le domaine de la numération des nombres entiers ne nous a pas permis de dégager des résultats probants concernant les pratiques évaluatives en mathématiques des professeurs des écoles de notre échantillon, si ce n’est le constat d’une grande disparité dans la complexité des tâches proposées. Il nous a néanmoins amenée à nous demander si les professeurs avaient toujours conscience de la complexité des tâches qu’ils donnaient à leurs élèves en évaluation. En effet, même si dans l’ensemble peu de tâches complexes ont été proposées, nous avons réalisé, après avoir interrogé les professeurs lors de l’entretien, que ceux qui en avaient proposé n’avaient pas forcément conscience de leur niveau réel de complexité et que cela pouvait avoir un impact sur les résultats des élèves les plus faibles.

Pour illustrer notre propos, nous présentons à la figure 8 une tâche de dénombrement de collections proposée à des élèves de CP :

Figure 8

***Exercice donné en évaluation en CP***

Pour répondre correctement à cet exercice, l’élève doit utiliser une connaissance généralement méconnue des professeurs : l’énumération (Briand, 1999). En effet, l’élève doit, pour chaque collection d’animaux, organiser son dénombrement et discerner les animaux déjà comptés de ceux qu’il reste à compter, sans en oublier. Il va sans dire que cette tâche est plus complexe que si l’élève avait à dénombrer ces mêmes collections d’animaux, mais séparément[15]. Comme les tâches de dénombrement présentes dans l’évaluation du professeur se réduisaient à cet exercice, il est aisément possible d’imaginer que le professeur n’a pas permis aux élèves les plus faibles de réussir cette tâche et qu’il n’a pas eu conscience de sa complexité.

Une autre tâche, considérée comme complexe par notre outil (FC2⇒2 et NC⇒2 pour les éléments soulignés), mais pas considérée comme telle par le professeur, est la tâche suivante (voir Figure 9) de comparaison de nombres entiers :

Figure 9

***Série de tâches de comparaison de nombres donnée en CM2***

Les nombres soulignés dans l’exemple de la figure 9 ne sont pas présentés de la même façon que les autres. Ce découpage par tranche de deux ou trois chiffres complexifie la tâche de comparaison. En effet, ce découpage non usuel des nombres peut amener l’élève à vouloir mettre au même « format » les nombres proposés avant d’appliquer une quelconque règle de comparaison, sans que cela lui soit indiqué et sans qu’il ait été alerté sur ce fait (d’où des niveaux plus élevés de facteurs 2 et 3). Nous avons donc cherché à savoir si le professeur avait choisi délibérément de complexifier ces deux tâches en le questionnant lors de son entretien. Sa réponse a été : « Je n’avais pas réalisé ce problème ; c’est simplement une faute de frappe. » Cette réponse est doublement problématique, dans la mesure où non seulement le professeur n’a pas conscience de choisir des tâches plus complexes, mais aussi qu’il n’a pas eu conscience de la complexité générée par la présentation inusuelle de ces nombres. Or, comme le résument Bastien et Bastien-Toniazzo (2004), « les choix que font les maîtres dans la présentation de l’exercice engendrent des contraintes qui sont déterminantes pour la réussite ou l’échec » (Vantourout & Goasdoué, 2014, p. 12-13). Cela met également en lumière le fait que les compétences en évaluation des professeurs sont indispensables pour assurer la validité des évaluations de classe. Si un professeur n’est pas en mesure de déterminer la complexité des tâches évaluatives qu’il propose à ses élèves, il ne peut être apte à concevoir des évaluations valides. Vantourout (2004) a déjà mis en lumière le rôle essentiel que jouent les connaissances disciplinaires et didactiques des professeurs lors de la correction d’évaluations en mathématiques, mais elles sont également indispensables lors de la conception des évaluations.

Il pourrait ainsi s’avérer que notre constat de faiblesse de niveaux des tâches mathématiques proposées en évaluation serait encore plus marqué, dans la mesure où les professeurs n’ont pas toujours conscience de la complexité des tâches qu’ils proposent et qu’ils n’identifient pas toujours les savoirs mathématiques en jeu dans leur résolution.

Les évaluations étudiées dans le cadre de cette recherche se sont réduites à celles proposées en fin de séquence, car ce sont les seules qui ont été fournies par les professeurs de notre échantillon. Nous n’avons donc pas étudié celles qui l’ont été dans le cours de la séquence sans support écrit, peu observables dans le cadre de la méthodologie adoptée. Il conviendrait donc, pour avoir une vision plus juste des pratiques évaluatives de professeurs des écoles, d’étudier ces autres évaluations de classe ainsi que la négociation didactique inhérente à toutes les évaluations proposées au cours de l’étude d’une notion, comme ont pu le faire Chevallard et Feldmann (1986).

Nous aurions également souhaité davantage exploiter d’autres paramètres caractérisant les professeurs en croisant les données que nous avons récoltées dans le questionnaire avec l’analyse des tâches évaluatives que nous avons réalisée. Le faible nombre de professeurs appartenant à telle ou telle catégorie n’aurait pas rendu crédibles nos résultats. Nous aurions ainsi pu voir si des éléments tels que le cursus des professeurs (scientifique ou non), leur expérience professionnelle (années d’exercice du métier), l’école où ils enseignent (en REP ou « centre-ville ») ou même leur genre pouvaient avoir un lien avec la nature et la complexité des tâches évaluatives proposées. En effet, nous sommes convaincue que les pratiques évaluatives des professeurs sont « très variables et indissociables de caractéristiques telles que le dispositif d’évaluation adopté, le genre, l’année d’études, les années d’expérience, la familiarité avec la politique d’évaluation promue par le district de l’école » (Cizek, Fitzgerald & Rachor, 1996, p. 159).

Conclusion

Notre approche didactique nous a permis de porter un regard particulier sur les pratiques évaluatives en mathématiques d’un échantillon de 25 professeurs des écoles, en considérant plus spécifiquement la nature et la complexité des tâches proposées dans des évaluations autour de la numération. Nous avons ainsi pu réaliser que les tâches évaluatives proposées par ces professeurs étaient d’un faible niveau de complexité et de compétence, et qu’elles correspondaient presque exclusivement à des tâches que les élèves avaient déjà réalisées lors de séances ayant précédé l’évaluation. Considérant comme Moss (2013) que la validité d’une évaluation dépend du choix approprié des tâches relativement aux savoirs à évaluer et du format adapté à la nature de ces tâches, nous pouvons remettre en question la validité globale de ces évaluations de classe, même si une étude plus précise et individuelle mériterait d’être réalisée pour l’affirmer avec plus de certitude. Nous entendons par là que les évaluations proposées en mathématiques par les professeurs des écoles de notre échantillon ne permettent pas de déterminer ce que leurs élèves savent réellement. En effet, réussir des tâches d’un faible niveau de complexité ne renseigne pas sur le niveau de résistance des connaissances et compétences des élèves devant des tâches plus complexes. De même qu’échouer à une tâche complexe ne signifie pas que l’élève n’a acquis aucune connaissance ou compétence.

Nous avons ainsi pu observer une grande disparité des pratiques évaluatives en mathématiques des professeurs des écoles, disparité appréhendée à travers les tâches qu’ils proposent à leurs élèves lors des évaluations. Ces résultats rejoignent ceux trouvés par de nombreux chercheurs dans d’autres pays (McMillan, 2003 ; Cizek, Fitzgerald & Rachor, 1996 ; Stiggins, 2001 ; Remesal, 2007 ; Suurtamm, Koch & Arden, 2010). Ce constat résulte immanquablement de la très grande liberté pédagogique accordée aux professeurs français, de l’absence de formation à l’évaluation et d’un manque d’encadrement dans ce domaine.

Il semblerait donc que les évaluations de classe relèvent, en France, d’une fonction plus sociétale que pédagogique (Coll & Remesal, 2009). C’est certainement pourquoi l’évaluation formative est loin d’être le modèle de référence pour qualifier l’évaluation pratiquée par les professeurs français, même si de récentes directives ministérielles[16] préconisent cette orientation pour évaluer les élèves en classe. Nous estimons donc qu’il est indispensable de former les enseignants à mieux évaluer leurs élèves en leur fournissant des outils didactiques favorisant une évaluation plus constructive du point de vue des apprentissages. Nous sommes également convaincue que l’évaluation peut être un vecteur d’apprentissage pour les élèves et un levier de développement professionnel pour les enseignants (Stiggins, 2001 ; Hao & Johnson, 2013), même si la France, qualifiée de « village gaulois » en matière d’évaluation dans l’enquête internationale du CNESCO sur l’évaluation (CNESCO, 2014), se trouve devant un défi qui semble encore plus difficile à relever.

Étude des pratiques évaluatives en mathématiques de 25 professeurs des écoles français : une approche didactique à partir de l’analyse des tâches données en évaluation

Note de l’auteure

Résumé

Abstract

Resumo

Introduction