Résumés
Résumé
Cet article décrit de manière sommaire les principaux modèles de vote stratégique avec un grand nombre d’électeurs, dits modèles d’élections de masse. Dans ces modèles, on suppose que l’électeur décide de son vote en fonction des pivots, c’est-à-dire des événements où son unique voix va faire une différence quant au résultat de l’élection. Les principaux messages de ces modèles sont illustrés avec des exemples simples; ils sont ensuite présentés plus en détail; on examine enfin leurs applications et limites, notamment en ce qui concerne l’économie expérimentale.
Corps de l’article
Introduction
Le 6 décembre 2015 a eu lieu le premier tour des élections régionales françaises. Il s’agissait d’un scrutin par listes fermées, les listes étant couramment désignées par le nom de leur tête de liste. Les scores (en pourcentage) dans la toute nouvelle région Alsace-Champagne-Ardenne-Lorraine – dite Grand Est – ont été les suivants :
Florian Philippot (Front national, FN), Extrême droite |
36,06 |
Philippe Richert (Union de la droite, UD), Droite |
25,83 |
Jean-Pierre Masseret (Union de la gauche, UG), Gauche |
16,11 |
Sandrine Bélier (Europe Ecologie Les Verts, EELV), Ecologistes |
6,70 |
Laurent Jacobelli (Debout la France, DLF), Droite |
4,78 |
Jean-Georges Trouillet (Unser Land), Régionaliste |
4,74 |
Patrick Péron (Front de gauche, FG), Extrême gauche |
3,07 |
Julien Wostyn (Lutte Ouvrière), Extrême gauche |
1,48 |
David Wentzel (Union populaire républicaine), Droite |
1,23 |
Seules pouvaient se présenter au second tour les listes atant obtenu au moins 10 % des voix au premier tour. La liste UG était la liste soutenue par le Parti socialiste. Afin de faire barrage au Front national, le Parti socialiste (PS) a demandé à J.-P. Masseret de ne pas présenter sa liste au second tour. J.-P. Masseret et ses colistiers sont passés outre et ont perdu, de ce fait, le label qu’ils avaient au premier tour. Au second tour restaient donc en lice trois listes : celle du Front national, celle de l’Union de la droite et celle conduite par J.-P. Masseret, désormais étiquetée Divers gauche (DG). Ceci a conduit à une situation inhabituelle : l’appel du PS et du gouvernement socialiste à voter pour la liste UD malgré la présence de la liste DG.
Que doit faire un électeur rationnel dans pareil cas? Quelles sont les prédictions faites par la théorie des élections de masse dans un tel cadre? Pourquoi le PS a-t-il besoin d’appeler ses électeurs à ne pas voter pour son propre candidat? Telles sont les questions auxquelles nous tenterons de répondre dans cet article.
Pour ce faire, il convient d’abord, avant de rappeler les définitions formelles, d’illustrer certaines prédictions de la théorie des élections de masse dans le cadre de l’élection de la région du Grand Est.
Il s’agit d’élire l’Assemblée régionale. L’élection en question suit une règle de proportionalité avec prime au vainqueur : le nombre de sièges attribués à chaque liste est proportionel à son score, avec une « prime » de 25 % des sièges pour la liste arrivée en tête. L’existence de cette prime importante ramène en pratique cette élection proportionnelle vers une élection de type majoritaire. En effet, la liste arrivée en tête a de fait de fortes chances d’être à elle seule majoritaire à l’assemblée, et en tout cas de faire élire le président de l’assemblée.
Supposons que le seul but des électeurs du deuxième tour est d’élire le président de la région[1], en d’autres mots, leur utilité dépend uniquement du candidat élu et non pas de la distribution des votes (qui, ceci dit, peut avoir une influence sur la répartition du pouvoir au sein du gouvernement). Pour simplifier, nous diviserons les électeurs en trois groupes ou types. Le premier d’entre eux rassemble les électeurs qui préfèrent la victoire du FN à celle des deux autres partis–on les appellera les électeurs de type FN. Les électeurs des deux autres types sont ceux qui ne veulent pas la victoire du FN mais qui sont partagés entre ceux qui préfèrent l’UD à DG et vice versa. Aucun des trois groupes ne rassemble plus de 50 % de l’électorat mais les électeurs de type UD et DG forment ensemble une majorité.
Les électeurs majoritaires se trouvent alors face à un dilemme. S’ils parviennent à se coordonner, ces électeurs peuvent imposer un de leurs candidats comme président. Ils ont forcément intérêt à se coordonner car en cas de mésentente, ils se retrouveront dans la situation qu’aucun d’eux ne souhaite : l’élection du candidat FN. Cette situation est donc très similaire à un exemple classique de la théorie du vote dit de la majorité divisée décrit par Myerson et Weber (1993)[2]. Nous la représentons par le tableau suivant.
Lorsqu’on représente l’utilité d’un électeur de type UD par le vecteur (0,10,9), cela signifie que cet électeur associe un paiement de 0 pour la victoire du parti FN, 10 pour celle du parti UD et de 9 pour celle de DG.
L’appel du PS et du gouvernement aux électeurs de type DG à voter pour UD est clairement un appel à la coordination des électeurs. Cette coordination semble souhaitable pour ces électeurs. En effet, si tous les électeurs votent de manière sincère (c’est-à-dire pour leur parti préféré), ceci conduit à la victoire du parti FN. Or, pour une majorité d’électeurs, cette issue est la moins souhaitable. Ceci dit, l’existence même de cette consigne suggère que la situation où chaque type d’électeur ne vote que pour son parti préféré est tout à fait possible. En effet, comme le démontrent Myerson et Weber (1993), les trois cas de figure (vote des électeurs UD-DG pour UD, vote des électeurs UD-DG pour DG, et chaque électeur vote pour son parti préféré[3]) sont des situations d’équilibre[4]. Ceci veut dire que la règle de la pluralité ne garantit pas la coordination des électeurs de manière systématique : en d’autres mots, cette règle ne fournit pas aux électeurs les bonnes incitations pour pouvoir se coordonner systématiquement sur un des partis/candidats préférés par la majorité.
Bien qu’il semble raisonnable, pour cette majorité, de se coordonner de manière collective, reste à savoir comment doit agir individuellement un électeur rationnel dans cette situation. Doit-il suivre l’appel du PS ou au contraire voter de manière sincère? Ce comportement optimal de l’électeur–dit rationnel–dépend de ses préférences et surtout de ses croyances par rapport aux chances de gagner des différents candidats.
L’exemple qui vient d’être développé n’est qu’un exemple, mais il est clair que ce type de situation est fréquent. Les élections fédérales canadiennes de 2015 fournissent un autre exemple récent de « majorité divisée ». Rappelons que, après son score historiquement bas de 18,9 % en 2011, le Parti libéral abordait les élections de 2015 en état de crise alors que le Nouveau Parti démocratique avait formé l’opposition officielle au Parti conservateur au pouvoir de 2011 à 2015. Dès lors, ceux qui voulaient voter contre le Parti conservateur avaient un choix stratégique à faire : le Parti libéral ou le Nouveau Parti démocratique. Au début de la campagne, le Nouveau Parti démocratique était annoncé grand gagnant. Mais cela s’est renversé en cours de campagne et c’est finalement le Parti libéral qui a gagné avec 39,5 % des voix. Son leader Justin Trudeau est donc devenu Premier ministre. L’histoire de cette campagne est en bonne part l’histoire de la coordination dynamique des électeurs anticonservateurs.
Existe-t-il des systèmes électoraux qui permettent aux électeurs de se coordonner correctement ou, au contraire, tout système doit-il mener inévitablement à des défaillances de coordination? Autant de questions auxquelles nous tâcherons de répondre en considérant principalement les élections à plus de deux candidats. À cet effet, la première partie de notre revue de littérature (section 1) sera consacré à ce que nous appelerons le modèle de base qui reprend en grande partie celui de Myerson et Weber (1993). Nous présenterons ensuite deux exemples simples pour illustrer les messages principaux de cette littérature (section 2). La troisième partie, plus technique, sera consacrée au calcul et à l’estimation des probabilités pivots dans les modèles binomiaux et de Poisson (sections 3.1 et 3.2). Enfin, nous discuterons des quelques applications des modèles de grandes élections comme les problèmes de coordination, le système à deux tours et les modèles d’incertitude agrégée, et des limites de ces modèles mises en évidence par l’économie expérimentale (section 4).
1. Le modèle de Myerson-Weber
Sera repris ici, en grande partie, le modèle proposé par Myerson et Weber (1993), en laissant de côté la plupart des arguments techniques. La spécificité du modèle présenté réside dans sa simplicité : les probabilités des événements pivot (ou probabilités pivot plus simplement) ne sont jamais calculées ni estimées. Le raisonnement stratégique des électeurs dépend de la très astucieuse condition d’ordre qui permet d’établir des ordres de grandeur de ces probabilités et donc de simplifier énormément le raisonnement stratégique. Nous étudierons plus tard deux méthodes d’estimation de ces probabilités proposées par Myerson (2000) et Laslier (2009). Mais il en existe bien d’autres, tels par exemple ceux de Ledyard (1984) et Cox (1994) qui estiment les probabilités pivot en utilisant des techniques combinatoires.
1.1 Structure du modèle
Les ensembles finis d’électeurs et de candidats sont respectivement désignés par Ɲ = {1,…,n} et χ = {a, b,…,k}. Notons que n est supposé être grand. Les préférences d’un électeur sont représentées par une fonction d’utilité u : χ → ![]() , où u(x) est égal à l’utilité que l’électeur obtient en cas de victoire du candidat x. Pour chaque électeur i ∈Ɲ et toute paire de candidats x, y ∈χ, x ≻iy ⟺ ui (x) > ui (y).
, où u(x) est égal à l’utilité que l’électeur obtient en cas de victoire du candidat x. Pour chaque électeur i ∈Ɲ et toute paire de candidats x, y ∈χ, x ≻iy ⟺ ui (x) > ui (y).
Les électeurs votent de manière simultanée en choisissant un bulletin dans un ensemble fini V de bulletins. Par exemple, si on applique la règle de la pluralité, chaque électeur vote pour un seul des candidats ou s’abstient. Il choisit donc un bulletin v = (va,…, vk) ∈ Vp où vx ∈ {0, 1} représente le nombre de points associé au candidat x et il y a au plus un vx = 1. Par exemple, à trois candidats, l’ensemble Vp des bulletins de pluralité est le suivant :
Si la règle est le vote par assentiment (voir Brams et Fishburn, 1983; Laslier et Sanver, 2010, entre autres) chaque électeur a le droit de donner un point à n’importe quel sous-ensemble de candidats. L’ensemble de bulletins autorisés sous cette règle, Va, est l’ensemble de bulletins v tels que vx ∈ {0, 1}. À nouveau à trois candidats, Va est tel que :
Si la règle de Borda est utilisée, l’électeur doit classer les candidats. On peut donc la représenter en définissant chaque bulletin par une liste de nombres b = (b1,…,bk) avec ![]() . L’ensemble Vb de bulletins est l’ensemble des permutations de b et l’abstention. Ceci implique qu’avec trois candidats, l’ensemble des bulletins est égal à :
. L’ensemble Vb de bulletins est l’ensemble des permutations de b et l’abstention. Ceci implique qu’avec trois candidats, l’ensemble des bulletins est égal à :
Pour toute paire de candidats x, y ∈ χ, la relation majoritaire M est définie ainsi : x est M-préféré à y, xMy, si et seulement si N(x, y) > N(y, x) , avec ![]() . Le gagnant de Condorcet (GC) est le candidat qui est M-préféré à tout autre candidat : x est le GC si et seulement si xMy pour tout y ∈χ \{x}. Son existence n’est pas garantie pour tout profil de préférences, c’est-à-dire qu’il existe des profils qui n’en possèdent pas (sauf si l’on fait des hypothèses de restriction de domaines comme l’unimodalité). De même, s’il existe un candidat X tel que tout autre candidat y est M-préféré à x, on dit que ce candidat est le perdant de Condorcet (PC).
. Le gagnant de Condorcet (GC) est le candidat qui est M-préféré à tout autre candidat : x est le GC si et seulement si xMy pour tout y ∈χ \{x}. Son existence n’est pas garantie pour tout profil de préférences, c’est-à-dire qu’il existe des profils qui n’en possèdent pas (sauf si l’on fait des hypothèses de restriction de domaines comme l’unimodalité). De même, s’il existe un candidat X tel que tout autre candidat y est M-préféré à x, on dit que ce candidat est le perdant de Condorcet (PC).
1.2 Comportement stratégique des électeurs
Chaque électeur maximise son utilité espérée et choisit, pour ce faire, un bulletin dans l’ensemble V. Nous supposerons tout au long de cet article que son vote n’a d’impact sur son paiement qu’à la condition de modifier le gagnant de l’élection. Afin de pouvoir déterminer l’utilité espérée des différents bulletins, un électeur a dès lors besoin d’avoir une opinion a priori sur les ordres de grandeur de ce type de situations, qui sont appelés les événements pivots.
Deux candidats sont ex aequo si leur score est le même. L’ensemble H décrit les paires non ordonnées de candidats. La paire {x, y} ∈ H est simplement notée xy avec xy = yx. Pour chaque paire xy ∈ H, la probabilité pxy est la probabilité de l’événement « les candidats x et y sont premiers ex aequo ». Le vecteur pivot p = (pxy)xy ∈ H représente les différentes probabilités pivots pour les différentes paires de candidats. On impose une symétrie de l’information de manière exogène : le vecteur pivot p est connu par tous les électeurs par hypothèse.
Étant donné le vecteur pivot p, un électeur qui choisit le bulletin v pense que : la probabilité d’être décisif entre y et x est proportionnelle à pxy × max{vx – vy, 0}.
Plus précisément, « être décisif entre y et x lorsqu’on choisit v » signifie que x remplace y comme gagnant de l’élection lorsqu’au lieu de s’abstenir, l’électeur choisit le bulletin v. Ce changement du gagnant ne peut arriver que si vx ≥ vy. Autrement dit, la probabilité d’être décisif entre y et x en choisissant le bulletin v est proportionnelle à vx – vy et pxy est le coefficient de proportionnalité. De manière symétrique, la probabilité d’être décisif entre x et y en choisissant le bulletin v si vy ≥ vx est aussi proportionnelle à la différence des scores vy ≥ vx et a le même coefficient de proportionnalité (pxy).
Cette hypothèse de symétrie est équivalente à supposer que la probabilité de l’événement « les candidats x et y sont premiers ex aequo » est égale à celle de l’événement « les candidats x et y sont les deux premiers classés et x a un point d’avance sur y » et aussi à celle de l’événement « les candidats x et y sont les deux premiers classés et y a un point d’avance sur x ». Myerson et Weber (1993) justifient cette hypothèse en affirmant qu’elle semble vérifiée lorsque l’électorat est suffisamment important. Elle n’est pas vérifiée dans d’autres modèles comme les jeux de Poisson.
L’utilité espérée Ui(v; p) de l’électeur i lorsqu’il choisit le bulletin v étant donné le vecteur pivot p s’écrit : ![]() .
.
Un profil de stratégies σ = (σi, σ– i) est une fonction de χ dans l’ensemble des distributions de probabilités sur V. Chaque σi décrit la probabilité avec laquelle l’électeur i choisit chaque bulletin v dans l’ensemble V. Le gain en utilité espérée pour l’électeur i lorsqu’il joue la stratégie (mixte) σi est égale à ![]() . Pour tout profil de stratégies σ, la proportion de l’électorat qui choisit le bulletin v est représentée par
. Pour tout profil de stratégies σ, la proportion de l’électorat qui choisit le bulletin v est représentée par
Par conséquent, le score du candidat x est égal à
Pour tout profil de stratégies σ, l’ensemble des gagnants probablesw(σ) ⊆ χ contient les candidats dont le score S(x; σ) est maximal.
1.3 Scores et pivots : la condition d’ordre
Jusqu’à présent, nous avons supposé que les anticipations des électeurs sont complètement déterminées par le vecteur pivot p. De plus, ce vecteur est exogène, il ne dépend d’aucun autre paramètre du modèle. Or, en général, les anticipations des électeurs sur les probabilités d’être pivot (ou plus généralement sur le possible impact de leur vote) dépendent en grande mesure des anticipations sur les scores des candidats. Autrement dit, si l’élection est serrée, c’est-à-dire si les deux candidats principaux ont des scores très proches dans les sondages, il semble naturel d’anticiper qu’un seul vote peut faire la différence. De la même manière, si un seul gagnant émerge des sondages, un électeur rationnel devrait déduire qu’il est peu probable que son seul vote aura un impact sur la victoire de ce candidat.
Pour prendre en compte cette intuition, Myerson et Weber (1993) font deux hypothèses.
La première de ces hypothèses porte sur les anticipations des électeurs à propos des probabilités des événements pivots où deux candidats arrivent premiers ex aequo. Les électeurs anticipent que si le candidat y a un score plus bas que le candidat x et si l’un des deux doit être premier ex aequo contre un troisième candidat z, il est nettement plus probable que ce soit x qui soit présent à l’ex aequo. C’est-à-dire, ils imposent une corrélation entre les scores des candidats et leurs probabilités pivot. Mathématiquement, cette corrélation implique que pour tout candidat z, le vecteur pivot p vérifie la « condition d’ordre » par rapport à ε ∈ (0, 1) pour le profil de stratégies σ si pour tout x, y ∈ χ,
La deuxième hypothèse sur les probabilités pivot porte sur les événements pivots avec plus de deux candidats. Plus précisément, on suppose que les événements où plus de deux candidats sont premiers ex aequo ont une probabilité négligeable par rapport aux probabilités pivot des événements où deux candidats sont premiers ex aequo. Un électeur peut donc simplement se concentrer sur les événements pivots à deux candidats et ignorer les autres types de pivot.
1.4 Concept d’équilibre
Pour tout vecteur pivot p, l’ensemble des meilleures réponses pour un électeur i est représenté par
Le support de la stratégie σi de l’électeur i représente l’ensemble des stratégies pures jouées avec probabilité positive dans σi : Supp(σi) = {v ∈ V | σi(v) > 0}. Une suite de vecteurs pivot {pε}ε→0 vérifie la condition d’ordre par rapport au profil de stratégies σ si, pour tout ε > 0, pε est un vecteur qui satisfait la condition d’ordre.
Définition 1.1 Le profil de stratégies σ est un équilibre si et seulement si :
il existe une suite {pε}ε→0 de vecteurs pivot avec pεxy > 0 pour tout xy ∈ H et tout ε > 0 qui satisfait la condition d’ordre par rapport au profil de stratégies σ et
pour tout bulletin v ∈ V et tout électeur i ∈Ɲ, v ∈ Suppi(σ) ⇒ v ∈ BRi(pε)pour tout ε > 0.
Remarques :
Vund représente l’ensemble des stratégies pures non dominées. Rappelons qu’une stratégie est (faiblement) dominée s’il en existe une autre qui ne donne jamais un pire paiement pour toute stratégie des autres joueurs. À l’inverse, une stratégie est non dominée si elle n’est pas dominée. Par exemple, toute stratégie sous la pluralité où l’électeur ne vote pas pour son candidat le moins préféré ou s’abstient est non dominée. Sous le vote par assentiment, une telle stratégie doit (i) approuver le candidat préféré de l’électeur et (ii) ne pas approuver son candidat le moins préféré. Avec Borda et juste trois candidats, un bulletin est non dominé si l’électeur donne 1 ou 2 points à son candidat préféré, et 0 ou 1 à son pire candidat[5]. Afin d’unifier les résultats, nous nous intéressons uniquement aux équilibres du jeu où les électeurs ne choisissent que des stratégies non dominées.
Vsinc représente l’ensemble des stratégies sincères pour chaque joueur. Pour la pluralité, être sincère implique voter pour son candidat préféré alors qu’avec le système de Borda, afficher son vrai classement est considéré comme sincère. Sous le vote par assentiment, est considéré comme sincère tout bulletin avec la propriété suivante : si l’on approuve un candidat, on approuve également tout candidat préféré à celui-ci.
On peut démontrer qu’il existe toujours un équilibre si le nombre de types (c’est-à-dire préférences cardinales) autorisé dans le jeu est fini. Cette restriction est importante car la preuve d’existence se base sur celle de l’équilibre propre (Myerson, 1978), qui elle se base à son tour sur le nombre fini d’agents.
Dans la littérature des modèles de grandes élections, on compare les règles de vote en comparant les ensembles d’équilibres qui y sont associés. Plus particulièrement, on s’intéresse à l’ensemble des candidats gagnants à l’équilibre. Par exemple, on s’intéresse à l’existence d’un équilibre où la victoire du gagnant de Condorcet est assurée. D’une certaine manière, cette notion de comparaison des règles de vote est similaire aux idées présentes dans la littérature de l’implémentation. En effet, l’objectif de la théorie de l’implémentation est de construire un mécanisme qui implémente une fonction de choix social soit dans un des équilibres générés par le mécanisme, (implémentation de Nash) soit dans tous (implémentation complète); voir Laslier et Sanver (2010) pour une introduction. La différence fondamentale entre ces deux approches repose sur le pouvoir de prédiction de l’équilibre de Nash (même en stratégies non dominées) : il est quasi inexistant dans les modèles d’élection puisque dès que le gagnant de l’élection a plus de 2 voix d’écart avec le second, le profil de stratégies correspondant est un équilibre. Afin d’établir des prédictions électorales, on se voit donc obligé de faire appel à des modèles plus sophistiqués où les croyances des électeurs sont liées aux scores attendus des candidats en lice, ce qui est d’ailleurs réaliste.
2. Deux exemples simples
Pour illustrer les principaux messages des modèles d’élections de masse, nous présenterons ici deux exemples adaptés de Myerson (2002) et Myerson et Weber (1993). Ils sont tous les deux très simples (deux types d’électeurs et trois candidats), mais ils résument bien certains messages de cette littérature. Ils ont, en outre, tous les deux la particularité d’avoir chacun un surnom : « Au-dessus de la mêlée » et « La pomme pourrie ». Dans le premier, un candidat est unanimement préféré, dans le second, un candidat est classé dernier dans les préférences de tous les électeurs.
On remarquera que les mêmes exemples peuvent être analysés en utilisant le concept, plus traditionnel, d’équilibre de Nash. Or, le concept d’équilibre de Nash n’est pas très informatif dans les modèles de vote dans le sens suivant : tout profil de stratégies où un candidat gagne par plus de deux points est un équilibre car aucune déviation individuelle ne peut modifier le résultat. Le concept d’équilibre utilisé ici (définition 1.1) est propre aux modèles de vote et tient compte des anticipations de probabilités pivot de manière explicite; comme montré par la suite, il raffine les équilibres de Nash et donne « peu » de prédictions possibles.
2.1 Au-dessus de la mêlée
Comme annoncé, cet exemple compare les règles de vote dans un scénario où un candidat est le meilleur choix pour tous les électeurs. Ce candidat est donc « Au-dessus de la mêlée » (Above the Fray) ce qui conduit à penser qu’un bon système de vote doit le choisir dans tout équilibre.
Il y a trois candidats, et deux types d’électeurs. Précisément, on suppose que les préférences de l’électorat sur les candidats {a, b, c} sont décrites par le tableau suivant :
Avec le vote par assentiment, toute stratégie non dominée donne un point au candidat préféré de l’électeur et aucun au dernier placé. La seule question qui se pose à l’électeur est de savoir s’il va approuver ou non son second candidat. On en déduit immédiatement que, dans tout équilibre, le candidat a est seul gagnant de l’élection. Sous Borda, a est également élu à l’équilibre.
Si la règle de vote utilisée est celle de pluralité, il existe aussi un équilibre où le candidat a est bien élu. Mais ce candidat n’est pas forcément élu dans tout équilibre. Par exemple, le profil de stratégies σ suivant définit un équilibre où il n’est pas parmi les gagnants probables :
Ce profil σ induit les scores suivants ![]() . La condition d’ordre implique donc que la probabilité pivot pbc devient infiniment plus probable que les autres lorsque ε → 0 pour toute suite de vecteurs pivot {pε}. Étant donné ce vecteur pivot, les électeurs de type A et B ont respectivement une unique meilleure réponse : voter pour b et pour c, ce qui démontre que σ est bien un équilibre. Le candidat préféré par tous ne reçoit aucune voix, tous les électeurs « rationnels » se basant sur la prophétie (autoréalisée) qu’il n’a aucune chance.
. La condition d’ordre implique donc que la probabilité pivot pbc devient infiniment plus probable que les autres lorsque ε → 0 pour toute suite de vecteurs pivot {pε}. Étant donné ce vecteur pivot, les électeurs de type A et B ont respectivement une unique meilleure réponse : voter pour b et pour c, ce qui démontre que σ est bien un équilibre. Le candidat préféré par tous ne reçoit aucune voix, tous les électeurs « rationnels » se basant sur la prophétie (autoréalisée) qu’il n’a aucune chance.
2.2 La pomme pourrie
La situation est ici diamétralement opposée à celle décrite dans « Au-dessus de la mêlée ». Cette fois, l’un des candidats est le pire choix pour tous les électeurs. Ce candidat est donc « Une pomme pourrie ». Il semble donc pertinent de penser qu’un bon système de vote ne doit pas le choisir dans aucun équilibre.
De manière plus précise, on suppose que les préférences de l’électorat sur les candidats {a, b, c} sont décrites par le tableau suivant :
Avec le vote par assentiment, il est facile de voir que toute stratégie non dominée donne un point au candidat préféré de l’électeur et aucun au dernier placé. Il s’ensuit que, dans tout équilibre, le candidat c ne reçoit aucun point et qu’il est donc exclu des gagnants de l’élection. Si la règle de vote utilisée est celle de pluralité, le même raisonnement s’applique. Toute stratégie non dominée ne donnant pas de points au dernier placé, le candidat c ne reçoit pas de point à l’équilibre et se trouve donc, en fait, exclu des gagnants probables de l’élection.
Mais, cette fois, le problème résulte de l’application d’autres règles de vote. Par exemple, avec Borda, on peut démontrer que le candidat c fait partie des gagnants probables, ce qui démontre que cette règle est loin d’être idéale. En effet, supposons qu’il existe un équilibre σ sous la règle de Borda où les scores sont tels que S(a; σ) > S(b; σ) > S(c; σ). Étant donné que le candidat c est classé dernier, la condition d’ordre implique que le pivot le plus probable a lieu entre les candidats a et b. Ceci suffit à déterminer la meilleure réponse des deux types d’électeurs. Ceux de type A votent (1,0,1/2) pour empêcher b de gagner et ceux de type B votent (0,1,1/2) pour faire barrage au candidat a. Or ceci implique que S(a; σ) = α, S(b; σ) = (1 – α) et S(c; σ) = (1/2). Or, nous avons supposé que α ≥ 1 – α. Si α > 1/2, alors S(c; σ) > S(b; σ) et si α = 1/2, les trois candidats sont ex aequo. Ceci montre qu’il n’y a donc pas d’équilibre avec des scores S(a; σ) > S(b; σ) > S(c; σ). En appliquant de manière itérative le même raisonnement aux différents ordres des scores, on démontre que c doit toujours être parmi les gagnants probables afin d’avoir un équilibre : sous la règle de Borda, des candidats peu souhaitables peuvent se retrouver systématiquement parmi les gagnants à l’équilibre.
3. Estimation des probabilités pivots
Nous nous sommes concentrés jusqu’à présent sur les intuitions du vote stratégique sans prendre en compte le calcul des probabilités pivot. Or, une partie importante de la littérature porte sur ce point précis, principalement en raison de sa complexité. Par calcul des probabilités pivot, on entend en effet l’estimation pour tout nombre d’électeurs, compte tenu de leurs actions, des ordres de grandeur des différents événements où un seul vote peut faire la différence. Les développements ci-dessous décrivent l’estimation de ces probabilités pivot dans deux modèles.
3.1 Pivots endogènes : le modèle binomial
Le modèle binomial, décrit par Laslier (2009), est similaire au modèle de base décrit précédemment. Les deux modèles supposent que le nombre d’électeurs est exogène et connu, et que leurs préférences sont connaissance commune. Dans les deux modèles, l’électeur n’est pas sûr des conséquences de son vote et son choix dépend des probabilités de pivot. La principale différence porte sur l’estimation de ces probabilités. Alors que Myerson et Weber (1993) vont simplement supposer que les électeurs connaissent les probabilités de pivot éxogènes et vont exploiter leurs ordres de grandeur pour déduire le comportement optimal des électeurs, Laslier (2009) décrit un mécanisme qui génère l’incertitude sur les scores des candidats. Cette incertitude va, à son tour, permettre aux électeurs d’estimer les probabilités pivot. Le mécanisme d’incertitude est particulièrement simple : chaque point donné à chaque candidat peut être effacé (ou simplement ignoré) avec une probabilité très faible mais strictement positive (Florida tremble). Cette probabilité d’être effacé implique que les scores des candidats suivent des lois binomiales indépendantes les unes des autres. Cette indépendance a un grand avantage : elle permettra par la suite de déduire un comportement particulièrement intuitif pour les électeurs sous le vote par assentiment (voir théorème 4.2).
De manière plus formelle, Laslier (2009) considère un modèle avec un nombre fini d’électeurs et de candidats (que nous représentons toujours par Ɲ de cardinal n et χ de cardinal k). Les préférences cardinales de chaque électeur sont représentées par un type t dans l’ensemble fini T. La proportion d’électeurs de type t dans l’électorat est donnée par r(t) avec ![]() . Le problème de décision individuelle est très similaire à celui du modèle de base car on suppose, à nouveau, que les événements où plus de deux candidats sont premiers ex aequo sont négligeables par rapport aux probabilités pivot des événements où deux candidats sont premiers ex aequo. Pour représenter l’idée d’une élection de masse, on étudie des réplications de l’électorat. En d’autres termes, lorsque l’électorat est νƝ, la proportion d’électeurs de type t est égal à
. Le problème de décision individuelle est très similaire à celui du modèle de base car on suppose, à nouveau, que les événements où plus de deux candidats sont premiers ex aequo sont négligeables par rapport aux probabilités pivot des événements où deux candidats sont premiers ex aequo. Pour représenter l’idée d’une élection de masse, on étudie des réplications de l’électorat. En d’autres termes, lorsque l’électorat est νƝ, la proportion d’électeurs de type t est égal à ![]() .
.
En outre, la probabilité qu’un point pour un candidat soit effacé est égale à q avec ![]() . Cette probabilité est indépendante (i) du candidat qui reçoit le point et (ii) du bulletin qui assigne ce point. De plus, elle est supposée être indépendante de ν.
. Cette probabilité est indépendante (i) du candidat qui reçoit le point et (ii) du bulletin qui assigne ce point. De plus, elle est supposée être indépendante de ν.
Exemple : Dans un contexte où χ = {a, b, c}, si l’électeur i choisit le bulletin (1, 1, 0) alors :
avec probabilité q2, le bulletin enregistré est (0,0,0)
avec probabilité q(1 − q), le bulletin enregistré est (1,0,0)
avec probabilité q(1 − q), le bulletin enregistré est (0,1,0)
avec probabilité (1 − q)2, le bulletin enregistré est (1,1,0).
Il s’ensuit que les scores de a et b suivent des lois binomiales B(1, 1 − q).
Comme dans le modèle de base, σ décrit un profil de stratégies et τ(v, σ) la proportion de l’électorat qui choisit le bulletin v. À la différence du modèle de base, S(x; σ) représente cette fois le nombre maximal de points que reçoit chaque candidat x dans le profil de stratégies σ et lorsque l’électorat est représenté par Ɲ.
Pour chaque point j dans S(x; σ), la variable aléatoire ηj, x est égale à 1 avec probabilité q et à 0 avec probabilité 1 – q. Nous représentons le score aléatoire du candidat x associé au profil de stratégies σ par S(x; σ) où
Lorsqu’on réplique l’électorat (μƝ), le score de x est au plus de νS(x; σ) et donc est une loi binomiale avec espérance (1 − q)νS(x; σ) et variance q(1 − q)νS(x; σ).
Un gagnant probable de l’élection est un candidat tel que ![]() .
.
Pour simplifier nous supposons que le nombre maximal de points qu’on peut donner à un candidat est 1. Dans ce cas, un événement pivot où un seul vote est déterminant pour décider le vainqueur de l’élection entre les candidats x et y est donc un événement tel que :
Dans ce modèle, tous les électeurs n’ont pas forcément les mêmes croyances sur les probabilités des événements pivots. On doit donc définir pour tout électeur i, le vecteur pivot pi = (pixy)xy∈H.
Ceci dit, on peut démontrer le résultat suivant.
Théorème 3.1 Quand l’électorat est suffisamment répliqué dans le modèle binomial, les différences entre les vecteurs pivots n’ont pas d’impact sur les meilleures réponses des électeurs.
Ce résultat nous permet de retourner à la notation plus simple et de parler simplement du vecteur pivot p = (pxy)xy∈H.
Pour tout profil de stratégies σ, le vecteur pivot p satisfait la condition d’ordre limite si pour tout candidat z,
Théorème 3.2 S’il n’y a pas d’ex aequo parmi les scores attendus des candidats, le vecteur pivot satisfait la condition d’ordre limite dans le modèle binomial.
3.2 Pivots endogènes : le modèle de Poisson
Les préférences de chaque électeur sont représentées par son type t qui appartient à l’ensemble fini des types. À nouveau, l’identité du gagnant des élections est l’unique déterminant de l’utilité des électeurs. Les préférences de type t sont représentées par un vecteur ut qui associe à tout candidat une valeur numérique. Comme dans le modèle précédent, r(t) représente la proportion de l’électorat de type t. Les vecteurs u = (ut)t ∈ Tut et r = (r(t))t ∈ T représentent les possibles utilités de l’électorat et leurs respectives proportions.
La principale originalité du modèle de Poisson est de considérer que le nombre d’électeurs est aléatoire. Un jeu de Poisson de taille n est un jeu où le nombre d’électeurs est une variable aléatoire : sa distribution suit une loi de Poisson de moyenne n[6]. La distribution de probabilité et son paramètre sont de connaissance commune.
Un jeu fini de Poisson de taille espérée n est donc représentée par (χ, T, n, r, u). L’expression « grand jeu de Poisson » fait référence au comportement asymptotique d’une suite de jeux de Poisson de taille espérée n lorsque n est suffisamment grand. Pour tout ensemble fini de bulletins V, Z(V) représente l’ensemble des profils d’action possibles. En d’autres mots, Z(V) est l’ensemble de vecteurs z = (z(v))v ∈ V tel que chaque composante x(v) est un entier positif.
Ces jeux sont caractérisés par les deux propriétés suivantes :
les actions des électeurs dépendent uniquement de leur information privée à l’équilibre (équivalence environnementale), et
le nombre d’électeurs qui choisissent deux bulletins donnés sont indépendants l’un de l’autre (indépendance des actions).
Ces deux propriétés, comme le montre Myerson (1998b), font d’eux un outil pratique pour travailler dans des jeux à taille variable. En effet, l’indépendance des actions nous permet de simplifier la description des profils de stratégies. Au lieu d’écrire σi pour représenter l’action de l’électeur i, nous écrivons simplement σt pour décrire l’action de n’importe quel électeur qui a un type t : σt(v) est la probabilité qu’un électeur de type t choisisse le bulletin v.
Pour tout profil de stratégies σ, la proportion de l’électorat qui choisit le bulletin v est maintenant représentée par
Nous écrivons τ(v) au lieu de τ(v; σ) pour simplifier les notations. Une fois déterminées les proportions de l’électorat qui choisissent les différents bulletins, la probabilité que le résultat de l’élection coïncide avec le vecteur z ∈ Z(V) est égale à :
Le score attendu d’un candidat x associé au profil σ s’écrit
où vx représente le nombre de points que donne le bulletin v au candidat j. Les candidats avec le plus grand s(;σ) sont les gagnants probables de l’élection lorsque σ décrit le comportement des électeurs. Le score de chaque candidat x, S(x; σ), est une variable aléatoire de Poisson de paramètre ns(x; σ).
Pour tout événement z ∈ Z(V), les vrais scores des candidats sont décrits par le vecteur sz = (sz(x))x∈X avec ![]() . Lorsque le profil de vote est z ∈ Z(V), on définit
. Lorsque le profil de vote est z ∈ Z(V), on définit ![]() comme l’ensemble de candidats avec le plus grand score. Si les ex aequo sont décidés par tirage au sort, la probabilité de victoire du candidat x dans le vecteur z ∈ Z(V) est égale à :
comme l’ensemble de candidats avec le plus grand score. Si les ex aequo sont décidés par tirage au sort, la probabilité de victoire du candidat x dans le vecteur z ∈ Z(V) est égale à :
Pour tout vecteur z ∈ Z(V) et tout bulletin v ∈ V, z + {v} représente l’événement où un bulletin v est ajouté au vecteur z.
L’utilité espérée d’un électeur de type t s’il choisit le bulletin v et le profil de vote est z s’écrit
Un profil de stratégies σ est un équilibre dans un jeu fini de Poisson si pour tout v ∈ V et tout ![]() . En d’autres mots, un équilibre dans un jeu fini de Poisson est une liste de stratégies, une par type, telle que tout électeur prend une décision optimale compte tenu des stratégies des autres électeurs et de ses croyances sur le nombre d’électeurs de chaque type dans l’électorat. Ces équilibres existent et ont des limites bien définies lorsque la taille espérée de l’électorat devient arbitrairement grande. Myerson (1998b) propose d’utiliser ces limites d’équilibre comme source de prédictions des comportements stratégiques dans des élections de masse.
. En d’autres mots, un équilibre dans un jeu fini de Poisson est une liste de stratégies, une par type, telle que tout électeur prend une décision optimale compte tenu des stratégies des autres électeurs et de ses croyances sur le nombre d’électeurs de chaque type dans l’électorat. Ces équilibres existent et ont des limites bien définies lorsque la taille espérée de l’électorat devient arbitrairement grande. Myerson (1998b) propose d’utiliser ces limites d’équilibre comme source de prédictions des comportements stratégiques dans des élections de masse.
Plus formellement, nous définissons les limites d’équilibre lorsque la taille espérée de l’électorat n tend vers l’infini. Une suite convergente d’équilibres est une suite d’équilibres {σn}n → ∞ de jeux finis de Poisson de taille n tels que les vecteurs σn convergent vers une certaine limite σ lorsque n → ∞. Cette limite σ est un équilibre de masse.
Pour tout bulletin v et toute paire de candidats x et y, nous introduisons les notations suivantes :
pivot(v, x, y) représente l’événement où rajouter un seul bulletin v fait basculer le gagnant de l’élection du candidat x au candidat y,
pivot(v, x, y)
 .
.pivot(x, y) représente l’événement où rajouter un seul bulletin en plus peut faire basculer le gagnant de l’élection du candidat x au candidat y ou vice versa avec pivot(x, y)
 .
.
Remarquons que les électeurs ne s’intéressent qu’aux événements précédemment décrits pour déterminer leurs meilleures réponses.
Lorsque n tend vers l’infini, la probabilité d’un événement pivot tend généralement exponentiellement vers zéro. Le concept d’ordre de grandeur (magnitude) d’un événement est souvent plus utile que celui de sa probabilité car il simplifie les calculs. Un résultat A est un sous-ensemble de Z(V) avec ![]() . Pour une suite convergente d’équilibres {σn}n → ∞, la magnitude μ[A] d’un résultat A est définie par l’égalité suivante :
. Pour une suite convergente d’équilibres {σn}n → ∞, la magnitude μ[A] d’un résultat A est définie par l’égalité suivante :
4. Applications et limites des modèles d’élections de masse
Sont décrites ici les applications principales des modèles de grandes élections et leurs limites. On présente de manière sommaire les leçons générales qu’on peut tirer de la comparaison des règles de vote dans les modèles précédemment décrits. On s’intéressera d’abord à l’agrégation des préférences et à la multiplicité des équilibres. Par souci de simplicité, on présentera deux résultats, vérifiés dans le modèle de base (Myerson et Weber, 1993) et leur robustesse dans les deux autres modèles est discutée. On portera ensuite notre attention sur les incitations à la sincérité données par les différents systèmes. Puis, on finira par apporter quelques remarques sur les expériences de vote.
4.1 Coordination et équilibres
Le premier résultat concerne la règle de la pluralité. Il illustre, en une certaine mesure, la loi de Duverger (Duverger, 1951) selon laquelle les scrutins uninominaux (comme la règle de la pluralité) ont tendance à soutenir l’émergence de deux partis, et seulement deux. Un large éventail de recherches a été consacré à cette loi, qui est vérifiée dans la plupart des systèmes uninominaux, à quelques exceptions près, dont le Canada[7].
D’un point de vue théorique, Duverger (1951) présente cette loi en argumentant que le nombre de partis politiques est réduit à deux par un processus naturel de fusion et élimination comme suit. Si un parti reçoit un nombre réduit mais significatif de votes (qui n’assure pas sa participation active au gouvernement), il se voit confronté à un futur électoral hasardeux. Il peut donc choisir de s’allier, ou même de fusionner, avec un des deux partis majeurs en échange d’un partage des gratifications de la victoire. Ceci est le résultat d’un calcul stratégique fait par les leaders des partis, où le résultat indirect de la compétition interne entre les membres du parti (Roemer, 2009). Si le parti ne suit pas cette idée de fusion, il court le risque de voir ses électeurs le déserter progressivement et le parti se verra ainsi éliminé de la compétition électorale. Cette deuxième possibilité est celle décrite par le théorème suivant.
Théorème 4.1 Supposons que les préférences des électeurs sont strictes dans une élection sous la règle de pluralité. Pour toute paire de candidats xy, il existe un équilibre où tous les électeurs votent pour leur préféré parmi x et y.
Ce résultat n’est pas particulièrement positif pour la pluralité : on peut l’interpréter comme une sorte de « chaos » en ce sens que pratiquement tout candidat peut gagner l’élection. En effet, dès lors qu’il n’est pas le perdant de Condorcet, on peut toujours construire un équilibre où il gagne. À l’équilibre, la mécanique de vote suivie par les électeurs est assez simple : s’il est de commun accord que l’effet le plus probable d’un vote est de départager les candidats x et y, alors un électeur rationnel et instrumental ne va voter que pour son candidat préféré parmi x et y. Ceci va, à son tour, assurer qu’il est de commun accord que seuls x et y ont des vrais chances de gagner l’élection. Ce théorème est aussi vérifié dans les modèles binomiaux et de Poisson.
Le second des résultats porte sur le vote par assentiment, où la mécanique de vote est bien différente.
Théorème 4.2 Supposons qu’il existe un gagnant de Condorcet dans une élection sous le vote par assentiment. S’il n’y a pas d’ex aequo parmi les scores attendus des candidats, alors
il existe un unique équilibre en stratégies pures, et
le seul gagnant probable est le gagnant de Condorcet.
Ce théorème est un argument solide en faveur du vote par assentiment car il montre que cette méthode aide les électeurs à se coordonner sur le bon candidat dès qu’il existe. Ce résultat est aussi vérifié dans le modèle binomial mais ne l’est pas dans les jeux de Poisson. Les corrélations entre les scores des candidats, inhérentes aux jeux de Poisson avec le vote par assentiment, empêchent d’obtenir la condition d’ordre (voir Núñez, 2010).
Le comportement des électeurs dans l’équilibre décrit par le théorème 4.2 est décrit par la règle du leader (ou Leader’s rule, voir Laslier, 2009), car chaque électeur se positionne par rapport au leader (ou parti avec un plus grand score attendu) pour décider de ses votes. Cette règle de comportement peut être énoncée comme suit. Soit a le candidat considéré par l’électeur comme le gagnant le plus probable (le « leader »). L’électeur vote pour (ou approuve) tout candidat qu’il préfère à a et il n’approuve aucun des candidats qu’il considère moins bien que a. Finalement, pour décider d’approuver ou non le candidat a lui-même, il compare a au gagnant le plus probable parmi le reste des candidats (le challengerb), il ne vote pour a que s’il préfère a à b. Cette règle mène à un comportement sincère de la part de l’électeur et est relativement simple cognitivement : ce sont les candidats les plus sérieux qui sont utilisés comme benchmark dans la décision d’approbation.
Afin de l’illustrer, nous considérons une élection à quatre candidats {a, b, c, d}, où σ est un profil de stratégies qui génère les scores attendus suivants : S(a; σ) > S(b; σ) > S(c; σ) > S(d; σ). Un électeur avec des préférences c ≻i a ≻i d ≻i b raisonne de la manière suivante. Comme a et b sont respectivement le leader et le challenger, il va voter pour a car il préfère a et b. Comme il préfère c à a, il va voter pour c. Et, finalement, il ne vote pas pour d car il préfère a à d. Sa meilleure réponse est donc de voter {a, c}. De même, un électeur avec des préférences c ≻i b ≻i d ≻i a a le bulletin {b ,c ,d}comme unique meilleure réponse.
4.2 Sincérité et strategy-proofness
Une conclusion nuancée semble se dégager des différentes analyses : le vote par assentiment mène souvent à des résultats plus consensuels et à une meilleure coordination des électeurs. Mais qu’en est-il de la révélation des préférences? Les grands théorèmes d’impossibilité du début des années soixante-dix véhiculent en effet un message très clair : toute règle de vote, indépendamment de sa complexité, peut mener un électeur rationnel à mentir sur ses vraies préférences. Ceci a été interprété maintes fois en disant que toute règle de vote est donc également nuisible. Quel est donc l’intérêt des modèles de grandes élections? Ce type de modèles répond-il à ce type de critique?
Le résultat suivant[8] met clairement en avant les propriétés remarquables du vote par assentiment.
Théorème 4.3 Dans toute élection sous le vote par assentiment dans le modèle binomial, s’il n’y a pas d’ex aequo parmi les scores attendus des candidats, alors tout électeur est sincère à l’équilibre.
On dit qu’un électeur est sincère s’il joue des bulletins sincères, c’est-à-dire qu’en votant pour un candidat, il vote aussi pour les candidats qu’il préfère à ce candidat.
Ce résultat peut sembler paradoxal et aller à l’encontre des impossibilités déjà mentionnées. Afin d’illustrer en quoi il n’y a pas de paradoxe et de montrer comment les deux types de résultats peuvent coexister, nous présenterons une discussion sur la notion de sincérité et celle, beaucoup plus classique, de strategy-proofness.
D’emblée, nous ferons remarquer que la méthode de vote par assentiment, à différence du vote à la pluralité ou à la Borda, est hors du modèle canonique du vote (voir Sanver, 2010 et Endriss, 2013 pour une discussion à ce sujet). En effet, pour toute règle à points, il existe une correspondance claire entre vote sincère et préférence. Afficher son meilleur candidat sous la règle de la pluralité est évidemment l’unique message sincère alors que la sincérité oblige l’électeur à afficher son vrai classement sous Borda. Ni la pluralité ni la règle de Borda ne garantissent un comportement sincère à l’équilibre dans les modèles de grandes élections, ce qui ne nous surprend pas car le théorème de Gibbard-Satterthwaite peut s’étendre au modèle de Poisson comme le montre McLennan (2011)[9]. McLennan (2011) démontre que toute fonction de choix social unanime et strategy-proof est une dictature dans les jeux de Poisson.
Le vote par assentiment, en revanche, ne s’inscrit pas dans ce schéma de pensée car il demande à l’électeur de choisir un ensemble d’alternatives qu’il considère comme acceptables. Il n’est donc plus tout à fait clair ce que veut dire « être sincère ». Le concept de sincérité est en relation mais n’est pas vraiment équivalent à celui de strategy-proofness. En effet, on peut démontrer que les stratégies non dominées avec le vote par assentiment avec trois candidats sont forcément sincères. La différence clé entre ce résultat et le théorème de Gibbad-Satterthwaite est la suivante. Avec le vote par assentiment, il existe différents messages sincères. Si un électeur préfère le candidat 1 au candidat 2 et le candidat 2 au candidat 3, et vote pour les deux premiers, il peut préférer le candidat 2 au candidat 1 et ce dernier au candidat 3. Il n’existe pas en conséquence un unique message sincère pour toute préférence[10]. Si on accepte que la sincérité est un bon critère pour évaluer les systèmes électoraux[11], on doit remarquer qu’il existe d’autres définitions de sincérité dans la littérature du vote par assentiment. La définition de sincérité utilisée dans le théorème 4.3 est empruntée de Brams et Fishburn (2005). Elle est la définition la plus commune et acceptée; elle est en outre intuitive. D’autres définitions sont données dans Merill et Nagel (1987) et Dowding et van Hees (2008).
4.3 Le système à deux tours
Le scrutin uninominal majoritaire à deux tours (ou système à deux tours plus simplement) est le système électoral le plus utilisé pour les élections présidentielles : 61 des 91 pays qui élisent de manière directe leur président ont instauré une variante du système à deux tours (Blais, Massicotte et Dobrzynska, 1997). Sous ce système, un candidat gagne l’élection au premier tour s’il obtient une majorité absolue (plus de 50 %) des voix. Si aucun candidat n’obtient la majorité absolue au premier tour, un second tour a lieu entre (au moins) les deux candidats ayant eu le plus grand score au premier tour. Le candidat majoritaire au second tour gagne l’élection.
On pourrait s’attendre à que ce système (i) soit plus performant que la règle de la pluralité quant à la révélation des préférences et de l’information, et (ii) donne plus de légimité démocratique au gagnant, dans le sens où tout gagnant est élu par la majorité des électeurs. À l’appui de ces idées, on peut argumenter que, puisqu’il existe une possibilité de coordination au deuxième tour, les électeurs vont voter au premier tour pour leurs candidats préféré (Riker, 1982; Cox, 1997; Piketty, 2000; Martinelli, 2002). D’un autre côté, on peut aussi imaginer que le système à deux tours peut induire un comportement stratégique au premier tour et mener au laminage du centre, comme discuté plus loin dans la section 5[12].
Malgré sa popularité dans le monde réel, l’approche formelle de ce système est relativement récente et limitée. Elle se cantonne au cas de trois candidats et, dans la plupart des cas, à des profils de préférences particuliers. Lorsqu’on analyse ce système en utilisant les équilibres des jeux de Poisson, il ressort que ses propriétés théoriques sont, au mieux, mitigées. Bouton (2013) et Bouton et Gratton (2015) mettent en évidence une grande multiplicité d’équilibres parmi lesquels on retrouve les équilibres duvergeriens (comme ceux décrits par le théorème 4.1 avec la règle de la pluralité) où deux candidats concentrent tous les votes. Dans ce type d’équilibres, un des candidats gagne directement au premier tour. On retrouve aussi des équilibres (dont l’existence n’est pas assuré pour tout profil de préférences) où trois candidats sont viables. On peut donc conclure que la légitimité démocratique du gagnant n’est pas a priori assurée : on peut juste exclure que le perdant de Condorcet soit élu à l’équilibre, ce qui est bien la moindre des choses.
La modélisation par les équilibres de Poisson est donc peu conclusive, en particulier parce que ce modèle ne permet pas de dire si certains équilibres sont plus plausibles que d’autres. En prenant un example spécifique (un profil de préférences particulier sous information privé), Martinelli (2002) obtient des résultats plus précis sur la comparaison entre la règle de la pluralité et le système à deux tours. Il démontre que le système à deux tours domine la règle de la pluralité dans le sens suivant : une majorité des électeurs obtient une plus grande utilité espérée dès lors que l’information sur les candidats n’est pas très précise.
4.4 Les modèles d’incertitude agrégée
Jusqu’à présent, nous nous sommes concentrés sur les modèles de vote stratégique avec incertitude essentiellement sur les probabilités pivot. Comme on a vu, l’incertitude sur le nombre d’électeurs ou sur la mécanique d’enregistrement donne lieu à des modèles où le vote des électeurs génère de manière endogène ces probabilités, qui sont clés dans le comportement des électeurs. Ceci dit, l’analyse décrite se base sur une hypothèse cruciale : les électeurs ont une connaissance commune et parfaite des candidats sur lesquels l’élection se joue. Plus précisément, ces modèles se basent en général sur l’idée que les types des électeurs (leurs préférences) sont tirés de manière indépendante suivant une distribution connue : cette indépendance implique une quasi-certitude des supports populaires respectifs des différents candidats lorsque l’électorat devient suffisament grand (par une application de la loi des grands nombres). En d’autres termes, de manière agrégée, un électeur connaît, de manière quasi certaine, les préférences de l’électorat.
Or, ceci peut sembler peu pertinent ou réaliste dans un cadre d’élection de masse. L’existence même de sondages et leur grand nombre en période électorale peuvent être mis en avant pour affirmer qu’au niveau agrégé, un électeur a toujours de l’incertitude sur la popularité des candidats en lice. Cette observation a mené à la naissance d’une littérature en pleine expansion sur les modèles dits d’incertitude agrégée. Ce type d’incertitude a été modélisée de deux manières principales dans la littérature.
Une possibilité pour introduire ce type d’incertitude est de supposer que les votes (ou les types des électeurs) sont tirés d’un ensemble de distributions de probabilité, chacune d’entre elles étant choisie avec une certaine probabilité. Les votes sont donc conditionellement indépendants (s’ils sont tirés de la même distribution), mais sont corrélés de manière non conditionelle car ils sont tirés a priori de distributions différentes. L’exemple suivant, repris de Myatt (2015), illustre très simplement l’idée d’incertitude agrégée dans le cadre d’une élection à deux candidats. Considérons une élection entre deux candidats a et b. Chacun des n électeurs préfère a à b ou le contraire (pas d’indifférence). Un électeur tiré au hasard préfère a avec probabilité 1 – p et b avec probabilité p; on dit que p est la popularité relative de b par rapport à a. Conditionellement à p, les types sont indépendants. En effet, si p est le même pour tous les électeurs, on se trouve dans un modèle sans incertitude agrégée car lorsque n devient suffisament grand, la loi des grands nombres nous confirme que le ratio des tailles de chaque groupe se rapproche de p/(1 – p). Or, si on suppose que p est tiré d’une densité f(⋅) avec une moyenne p, on crée de l’incertitude agrégée. De manière rationelle, chaque électeur révise ses croyances sur les préférences des autres électeurs, conditionellement à la réalisation de son propre type : il y a donc de l’incertitude agrégée. Good et Mayer (1975) font partie des premiers travaux à identifier l’importance de cette sorte d’incertitude dans le calcul des probabilités pivot (ce résultat a été aussi souligné par Chamberlain et Rothschild, 1981; Myatt, 2007 et Mandler, 2012 montrent comment ceci va modifier la mécanique électorale dans le modèle de l’électeur rationnel). Fisher et Myatt (2002) mettent en évidence, dans un cadre expérimental, que les électeurs associent une importance moindre aux signaux publics que celle prédite par les modèles théoriques. Fisher et Myatt (2014) calibrent leur modèle sur des enquêtes conduites en Angleterre et montrent que, si l’incertitude agrégée est suffisament forte, le pouvoir prédictif théorique devient élevé. Bouton, Castanheira et Llorente-Saguer (2016b) complémentent les études précédentes en isolant l’effet de l’incertitude agrégée et parviennent à démontrer que l’existence (et non pas l’intensité) de l’incertitude agrégée suffit à expliquer l’existence d’équilibres non duvergeriens.
L’autre choix principal de modélisation de l’incertitude, qui est plus proche du modèle dit du jury de Condorcet, consiste à supposer que les électeurs sont incertains de leurs propres préférences. Les contributions de Austen-Smith (1996), Feddersen et Pesendorfer (1996) et Myerson (1998a) font partie des papiers pionniers dans cette approche, qui suppose qu’une des composantes des préférences est commune à tous les électeurs (on parle de valeurs communes). La valeur de cette composante n’est pas éxogène, elle va dépendre de l’état du monde. Par exemple, dans un jury, un juré préfèrera la condamnation ou la relaxe suivant l’état du monde (culpabilité ou innocence) dont il n’est pas certain.
Plus précisément, on suppose qu’il existe un certain nombre d’états du monde mais aucun des électeurs ne peut l’observer directement. Chaque électeur reçoit juste un signal sur le véritable état de monde (son information privée) qui est positivement corrélé avec la vérité. Son utilité espérée dépend donc de ses croyances. Les informations privées reçues par chaque électeur lui sont propres. L’objectif de l’élection est dorénavant d’agréger les informations individuelles, ce qui contraste avec l’agrégation des préférences qui est l’objectif des modèles sans incertitude agrégée. En utilisant cette approche, on obtient des prédictions plus réalistes sur la participation électorale à l’équilibre comme montré par Castanheira (2003) ou sur la coordination électorale comme un outil de communication de l’électorat (Piketty, 2000). On peut observer également dans ces modèles l’émergence, sous la règle de la pluralité, d’équilibres stables non duvergeriens, où les votes ne sont pas concentrés sur uniquement deux candidats, comme le montrent Bouton et Castanheira (2012), et Bouton, Castanheira et Llorente-Saguer (2016a). En outre, cette incertitude agrégée, alliée aux valeurs communes, peut parfois résoudre les problèmes de coordination souvent présents dans les contextes électoraux. En effet, dans la situation de la majorité divisée, le vote par assentiment mène à une aggrégation complète de l’information si les valeurs communes sont suffisament présentes. L’idée selon laquelle le vote par assentiment mène à une nette amélioration de l’agrégation de l’information par rapport à la plupart des règles de vote émerge aussi de la comparaison des règles de vote établie par Goertz et Maniquet (2011). Ces résultats théoriques sont confirmés par Bouton, Castanheira et Llorente-Saguer (2016a) qui comparent les règles de pluralité et d'assentiment dans un cadre expérimental.
Pour conclure cette section, on se doit de mentionner l’étude des référendums multiples (Ahn et Oliveros, 2012), l’extension du jury de Condorcet à plusieurs jurys proposée par (Ahn et Oliveros, 2012) ainsi que le modèle de Bhattacharya (2013) qui donne des conditions pour l’équivalence des prédictions électorales des modèles sans et avec incertitude agrégée, tous les trois se basant sur des techniques similaires à celles précédemment décrites.
4.5 Le vote et l’économie expérimentale
Comme on le voit, la théorie économique du vote fait grand cas d’un raisonnement assez spécifique prêté à l’électeur et qui consiste à envisager seulement le cas, même très peu probable, où son unique voix va faire une différence quant au résultat de l’élection; le « résultat » étant d’ailleurs le plus souvent entendu dans un sens assez étroit : qui est élu[13]. Or ce raisonnement entre souvent en contradiction avec d’autres motifs de vote, tout particulièrement avec la norme sociale qui veut qu’une élection soit une « consultation » dans laquelle chaque citoyen est supposé indiquer honnêtement son opinion (Fiorina, 1976; Brams et Fishburn, 1983; Blais et Young, 1999; Blais, 2000). La pertinence pratique des théories basées sur les événements pivots est donc tout sauf évidente et doit être validée empiriquement.
Plus précisément, deux éléments, à ne pas confondre, peuvent faire douter de la validité de cette théorie. D’une part, comme on vient de le dire, d’autres normes que la rationalité instrumentale peuvent déterminer les comportements. D’autre part, même un électeur désireux de suivre ce chemin de la rationalité peut tout simplement ne pas être convaincu par un raisonnement qui aboutit à baser son action sur un événement très improbable. Cette faute logique est commune, et correspond à une limitation cognitive connue : la difficulté du raisonnement conditionnel (Evans, Newstead et Byrne, 1993). Cette limite s’impose sans doute de manière d’autant plus forte que les recommandations « rationnelles » semblent parfois (on en donnera des exemples) contre-intuitives, voire « tirées par les cheveux ».
4.5.1 La participation
En laboratoire
Dans le modèle économique instrumental standard, la participation à une élection a un coût et la décision de s’abstenir ou pas relève d’un calcul coût-bénéfice standard, dans lequel le coût est fixe et le bénéfice dépend de cette fameuse probabilité « pivot » qu’un unique vote fasse une différence (Riker et Ordeshook, 1968; Ledyard, 1984). On a par conséquence cherché à valider, ou invalider, la théorie à propos de la participation.
Les prédictions qualitatives sont les suivantes. (i) Au premier ordre, la participation devrait être minuscule dans les élections politiques (car les probabilités objectives d’égalité exacte dans les élections de masse sont de fait minuscules). Cette prédiction théorique est clairement réfutée. (ii) La prédiction de second ordre est que la participation devrait être plus importante lors des élections les plus disputées. Ceci semble être le cas (Blais, 2000).
L’analyse coût-bénéfice ne permet donc pas d’expliquer pourquoi les électeurs participent aux élections réelles, mais ce qui peut être compatible avec ces observations est l’existence d’une frange de la population, qui obéisse aux prédictions qualitatives de cette théorie et ne se déplace donc que pour les élections les plus disputées, l’essentiel de la population obéissant à d’autres motifs.
Un test plus rigoureux de la théorie économique de la participation peut se faire en laboratoire. Il consiste à mettre les électeurs dans une situation dans laquelle les motifs politiques et sociaux sont effacés et seul reste l’intéressement au résultat. On donne ainsi toutes ses chances au raisonnement rationnel instrumental de se développer sans interférence avec d’autres normes. Ceci est facilement réalisé en laboratoire. Dans la version la plus simple (Schram et Sonnemans, 1996), on organise des jeux (le mot élection n’est pas prononcé) au cours desquels les participants, répartis dans deux groupes, doivent payer pour acheter des jetons (le mot vote n’est pas prononcé). La décision d’acheter un jeton est individuelle mais c’est le groupe qui achète le plus de jetons qui gagne.
De nombreuses variations sur ce thème ont été réalisées en laboratoire (Schram et Sonnemans, 1996; Tyran, 2004; Levine et Palfrey, 2007; Sauger et al., 2012; Blais et al., 2014). On observe en laboratoire un phénomène similaire à ce qui est observé en réalité. Premièrement, la participation est trop élevée par rapport aux prédictions de la théorie rationnelle (qui sont ici précises et quantitatives). Ceci constitue une réfutation d’autant plus forte que le protocole est destiné à donner toutes ses chances à cette théorie : les sujets sont en quelque sorte payés pour cela et les effectifs étant faibles, les probabilités d’être pivot sont réellement non négligeables, contrairement aux élections politiques réelles. Deuxièmement, les variations observées pour la participation suivant les paramètres du modèle, par exemple le nombre de participants, sont qualitativement conformes à la théorie (et à l’intuition aussi, d’ailleurs).
Sur le terrain
De nombreuses expériences ont été réalisées sur le terrain, destinées à comprendre les déterminants de la participation. Ces expériences se placent dans une longue tradition de la science politique, notamment américaine. En étudiant l’efficacité relative des diverses manières d’appeler les électeurs à participer, on démontre l’importance des effets de pression sociale. Pourquoi les électeurs votent-ils? La réponse est souvent : parce que les voisins regardent. Certaines de ces expériences sont très spectaculaires et convaincantes. Cependant, comme elles doivent assez peu à la science économique, nous ne les discutons pas ici. Le lecteur intéressé pourra lire par exemple Green et Gerber (2008).
4.5.2 Le vote stratégique
La théorie du vote « pivot » se révèle donc peu utile, voire clairement insuffisante, pour rendre compte de la participation électorale. Mais, bien entendu, ceci ne préjuge pas de sa capacité à expliquer tout ou partie des comportements des électeurs une fois qu’ils se sont déplacés pour aller voter ou, plus généralement, une fois qu’ils se sont acquitté du coût ou qu’ils ont retiré le bénéfice social de la participation. On s’intéresse donc maintenant aux expériences sur le vote rationnel au sens du choix « stratégique » du bulletin.
Deux branches de la littérature méritent d’être distinguées. La première s’intéresse aux élections à deux candidats. Le comportement stratégique dans le cas de deux candidats seulement, et sous les règles de vote usuelles, semble aller de soi : chacun vote pour le candidat qu’il préfère, compte tenu de son information. Une littérature de théorie des jeux s’est cependant développée à partir d’un paradoxe mis en lumière par Austen-Smith et Banks (1996) et Feddersen et Pesendorfer (1996), et lié à la « logique de l’événement pivot » dans les situations d’incertitude. Plus précisément, en présence d’information asymétrique et deux candidats, certains électeurs peuvent choisir à l’équilibre de voter contre leur meilleur candidat, de façon à déléguer la décision aux électeurs informés. Cette problématique a eu une abondante descendance théorique, et a fait l’objet de quelques tests expérimentaux en laboratoire (Guarnaschelli, McKelvey et Palfrey, 2000).
Le cas de deux candidats (décision collective binaire), bien que particulièrement pertinent aux États-Unis, est très restrictif et conduit à négliger une dimension importante des procédures démocratiques, à savoir les différentes manières d’adapter le principe majoritaire aux situations non binaires. On va donc surtout s’attarder sur les expériences traitant des élections entre plus de deux candidats.
Disons tout de suite que, contrairement à ce qui se passe à propos de la question de la participation électorale, la théorie économique rationnelle apporte des éclairages intéressants sur la question du choix du bulletin.
La théorie du vote rationnel est souvent identifiée à l’idée de « désertion des extrêmes ». Si on sait à l’avance quels sont les deux candidats qui vont probablement arriver en tête, voter pour un troisième candidat est inutile. Dans un vote à la pluralité simple (First Past the Post), la prédiction théorique est que deux candidats seulement reçoivent un nombre significatif de suffrages (Cox, 1997). En théorie ces candidats peuvent être quelconques – un cas typique d’une multiplicité d’équilibres –, ce qui nécessite une coordination entre les électeurs. Ce point est résumé en théorie par le théorème 4.1 vu plus haut. En pratique cette coordination se fait par le biais de l’histoire, les sondages d’opinion et les contributions électorales (voir Rietz, Myerson et Weber, 1973), et aboutit généralement à ce que les candidats extrêmes soient marginalisés.
Cette logique se vérifie très facilement en laboratoire avec le vote à la pluralité simple; voir par exemple Forsythe et al. (1993). On peut en particulier bien voir en laboratoire, en répétant les élections, comment un électorat se focalise progressivement sur une paire de candidats, d’une manière qui peut paraître inéluctable aux participants alors même que la paire de candidats qui émerge est en réalité aléatoire et varie effectivement, d’une session à une autre.
Du point de vue de l’électeur, la logique de la désertion des candidats non viables est en effet particulièrement simple dans le cas de la pluralité. Elle ne requiert que des informations de base sur les chances des différents candidats et aboutit à une recommandation évidente : voter en faveur de celui qu’on préfère entre les deux principaux candidats. Mais il en va tout autrement avec les autres règles de vote, et tout particulièrement avec la règle la plus commune pour les élections politiques destinées à élire un candidat, à savoir le système majoritaire à deux tours.
Le calcul rationnel du choix du bulletin au premier tour d’une élection à deux tours peut se révéler étonnamment complexe. Premièrement il doit intégrer des anticipations sur ce qui peut se passer au premier tour ainsi que dans les différents seconds tours envisageables. Deuxièmement il doit être du type backward induction (induction rétrograde), c’est-à-dire déduire ce qu’on veut obtenir au premier tour des conséquences de notre choix sur le second tour et tout ceci dans le cadre de raisonnements « pivots », basés sur des événements très peu probables.
L’économie expérimentale a montré depuis longtemps que les raisonnements par induction rétrograde sont peu utilisés en pratique. Ceci se vérifie à propos des élections à deux tours. Suivant les circonstances, les prescriptions rationnelles pour le vote à deux tours sont parfois intuitives, comme pour un vote à un seul tour, et parfois contre-intuitives, en invitant par exemple à faire passer au second tour un candidat, non pas parce qu’on veut le voir élu, mais, au contraire, parce qu’il a moins de chance qu’un autre de faire battre notre candidat préféré. Van der Straeten, Laslier et Blais (2013) montrent en laboratoire que les électeurs suivent, dans des élections à deux tours, les recommandations stratégiques si et seulement si ces recommandations se déduisent de raisonnements relativement simples. Les raisonnements sophistiqués n’opèrent pas.
Il existe quelques expériences de laboratoire à propos d’autres règles de vote, qui présentent un intérêt théorique et/ou sont utilisées dans certains pays : la règle de Borda, le vote par approbation, le vote alternatif. Certains de ces travaux sont décrits dans cette revue (Igersheim, Baujard et Laslier, 2017). Sur la question du vote rationnel, ces travaux confirment dans l’ensemble ce qu’on vient d’esquisser : en laboratoire, les participants votent de manière rationnelle tant que le raisonnement rationnel n’est pas trop sophistiqué. Si le raisonnement stratégique est trop complexe, les électeurs ne votent pas nécessairement de manière naïve, mais ils se reposent sur des heuristiques partiellement rationnelles.
Expériences hors du laboratoire
Rappelons que les études en laboratoire donnent toutes ses chances au modèle économique de calcul des bénéfices, les incitations étant, aussi purement que possible, monétaires. Il est donc important de ne pas se limiter à cette catégorie d’observations. Quelques expériences ont été faites, lors d’élections politiques, sur le terrain ou en ligne, à propos des questions soulevées précédemment. On peut ainsi étudier comment différentes règles de vote sont utilisées par les électeurs. Pour compléter ce qui a été dit dans la partie théorique, nous reprenons maintenant un des deux exemples déjà étudiés (« Au-dessus de la mêlée ») et abordons l’exemple classique du « laminage du centre ».
La situation décrite dans « Au-dessus de la mêlée », où un candidat (parmi trois) est considéré comme meilleur par tous les électeurs, ne se retrouve pas aussi simplement dans la réalité politique. Cependant l’équilibre théorique conduisant à la non-élection d’un tel candidat sous le vote à la pluralité décrit une logique dont il n’est pas exclu qu’elle puisse se mettre en place en réalité. Il s’agit simplement de l’idée qu’un candidat, même très bon, ne reçoit aucun vote parce que chaque électeur, pour ne pas perdre sa voix inutilement, vote pour celui qu’il préfère entre deux autres candidats, pourtant tous les deux moins bons. La théorie nous indique que ceci est possible avec la pluralité, mais pas avec le vote par approbation, car sous le vote par approbation, voter pour un candidat n’empêche pas de voter aussi pour un autre.
Toutes les expériences contrastant les comportements des électeurs sous les systèmes uninominaux (comme le vote à la pluralité) et multinominaux (comme le vote par approbation et plus généralement les systèmes par évaluation) confirment la validité de cette idée théorique. Par exemple, les électeurs à qui on offre la possibilité, pourtant déstabilisante, de voter pour plusieurs candidats, se saisissent de cette possibilité de manière intelligible et non triviale. Il s’ensuit que les candidats ne risquent plus, avec ces règles, d’être absorbés par de tels pièges spéculaires de non-viabilité. Ceci a été observé non seulement en laboratoire (Van der Straeten et al., 2010) mais aussi lors d’expériences in situ ou en ligne et dans des circonstances variées (Europe et Afrique, élections présidentielles ou législatives). Voir Laslier et van der Straeten (2004), Baujard et al. (2013), van der Straeten, Laslier et Blais (2013), Kabré. Laslier et Wantchekon (2015) et les nombreuses références décrites dans Igersheim, Baujard et Laslier (2017).
L’exemple de la « pomme pourrie » mentionné plus haut est intéressant dans le cas du vote suivant la règle de Borda. Cette règle étant pratiquement inusitée pour des élections de masse, nous ne nous y attardons pas et passons à un problème plus courant dit le « laminage du centre ».
Il s’agit du phénomène suivant. La désertion des extrêmes fait se reporter les voix des électeurs d’extrême droite sur un candidat de la droite modéré et celles des électeurs d’extrême gauche sur un candidat de la gauche modérée. Ce gonflement des voix récoltées au premier tour par deux candidats modérés fait qu’un candidat centriste ne passe jamais l’épreuve du premier tour. Il ne gagne donc jamais l’élection alors même qu’il aurait gagné au second tour contre n’importe quel adversaire : il gagnerait face à un candidat de droite, avec l’apport des voix de gauche et il gagnerait contre un candidat de gauche, avec l’apport des voix de droite.
Ce phénomène paradoxal est typique du système à deux tours et a une importance réelle; il semble avoir structuré la vie politique française pendant longtemps. On voit que la logique prêtée aux électeurs est bien celle du vote rationnel et des événements pivots, en fait assez semblable à celle décrite dans « au-dessus de la mêlée ». Cette logique s’applique au vote alternatif comme au vote à deux tours [14]. Au contraire, les expériences montrent que cette logique n’a plus cours dans le vote par approbation et les systèmes voisins.
L’ensemble de ces travaux dresse un tableau nuancé des comportements des électeurs, qui n’apparaissent ni naïfs ni infiniment calculateurs.
Conclusion
Nous avons traité de la littérature théorique sur les élections de masse en décrivant ses principales méthodes et conclusions, en trois parties.
La première partie, la plus classique, s’appuie sur le concept de pivot et de vote instrumental. Son objectif est de comprendre les raisonnements stratégiques d’un électeur qui tient compte des probabilités des pivots et anticipe les conséquences dans un cadre d’élection de masse. Avec différents degrés de sophistication mathématique, elle dresse une comparaison des règles de vote. Il en ressort que, sous la plupart d’entre elles, on peut s’attendre à un grand nombre d’équilibres et donc à une grande perméabilité des résultats électoraux à l’information dont disposent les électeurs. On remarquera que deux des règles les plus utilisées en pratique, comme la règle de la pluralité et le système à deux tours, appartiennent à cette catégorie. Par contraste, le vote par assentiment semble assurer une meilleure agrégation des préférences dans le sens où, sous des hypothèses raisonnables, le seul équilibre mène à l’élection du gagnant de Condorcet (s’il en existe un).
La deuxième partie, plus récente et dite de l’incertitude agrégée, s’attaque à une des faiblesses des premiers travaux. Plus précisément, elle relâche l’hypothèse selon laquelle, dans une élection de masse, un électeur rationnel est presque certain des préférences des autres électeurs. Ce faisant, elle obtient des résultats plus réalistes et explique mieux des phénomènes souvent peu ou mal compris comme la participation électorale. Ceci dit, étant donné qu’il s’agit d’une littérature en pleine expansion, on dispose pour l’instant de peu de travaux et la plupart d’entre eux portent sur des situations particulières. On a donc du mal pour l’instant à tirer des conclusions claires; en d’autres termes, il s’agit d’une littérature prometteuse qui devrait permettre de résoudre certaines difficultés posées par le modèle de l’électeur rationnel.
La dernière partie a trait à l’expérimentation. Elle cherche à (in)valider le modèle du vote rationnel et à proposer des alternatives qui décrivent, de manière moins caricaturale, le comportement dans l’isoloir. Elle met en avant certaines difficultés du modèle rationnel à propos de la participation électorale ou de la logique de l’induction rétrograde (souvent utilisée dans les approches théoriques des systèmes de vote à plusieurs tours). Par contre, elle semble valider certains aspects importants du vote stratégique comme la désertion des extrêmes où les problèmes de coordination. Cette littérature arrive, en d’autres mots, à la conclusion que les électeurs ne sont ni naïfs, ni trop sophistiqués dans leurs raisonnements.
Parties annexes
Remerciements
Nous remercions Jérôme Lang pour l’exemple des élections du Grand-Est, développé dans Lang (2015), ainsi que pour ses commentaires et Damien Bol pour ses renseignements sur les élections canadiennes. Nous remercions également l’éditeur et deux rapporteurs pour leurs nombreuses remarques et suggestions et l’ANR-14-CE24-0007-01 CoCoRICo-CoDec par son soutien financier.
Notes
-
[1]
Supposer que les électeurs s’intéressent uniquement au gagnant de l’élection et non pas aux pourcentages obtenus par les différents partis est une hypothèse simplificatrice, qui est utilisée de manière quasi exhaustive dans les modèles d’élections de masse, à quelques exceptions près (voir par exemple Núñez et Xefteris, 2015). Notons cependant dans le cadre de l’élection du Grand Est, la représentation obtenue in fine dans la région a une certaine dose de proportionnalité.
-
[2]
L’élection présidentielle américaine de 1912 est souvent citée comme exemple de ce type de divisions. Borda (1781) analyse également un problème similaire.
-
[3]
Ce dernier type d’équilibre, où les votes ne sont pas concentrés sur deux des candidats, est souvent instable comme démontré par Fey (1997), dans un modèle d’élections à la Myerson et Weber (1993).
-
[4]
À l’équilibre, aucun électeur n’a intérêt à dévier de manière unilatérale étant donné son information et les bulletins choisis par les autres électeurs.
-
[5]
Voir Dellis (2010) pour une caractérisation des stratégies non dominées pour les règles à point.
-
[6]
La probabilité qu’une variable aléatoire de Poisson de paramètre n soit égale à l est de
 , pour tout l entier positif.
, pour tout l entier positif. -
[7]
On peut citer entre autres les travaux sur les tests empiriques et les modèles théoriques comme par exemple ceux de Riker (1982), Rijer (1986), Feddersen (1992), Fey (1997) et Forand et Maheshri (2015).
-
[8]
Ce résultat n’est pas vérifié dans le modèle de Poisson comme montré par Núñez (2014).
-
[9]
Voir aussi les autres extensions récentes des théorèmes d’impossibilité comme celles de Campbell et Kelly (2009), Campbell et Kelly (2013), Chatterji et Sen (2011) et Man et Takayama (2013).
-
[10]
Wolitzky (2009) fait une analyse intéressante sur la différence entre strategy-proofness et sincérité dans le vote.
-
[11]
Elle ne garantit pas une agrégation satisfaisante des préférences même avec le vote par assentiment comme le montrent Núñez (2010), De Sinopoli, Dutta et Laslier (2006). Dans un cadre différent, la littérature sur le théorème du jury de Condorcet (Feddersen et Pesendorfer, 1996; Feddersen et Pesendorfer, 1997; Feddersen et Pesendorfer, 1998; Myerson, 1998) suggère que le vote insincère peut mener à un meilleur résultat que le vote sincère. En effet, quand les électeurs ne sont pas sincères, le meilleur candidat est le seul gagnant probable même lorsque l’information est biaisée.
-
[12]
Voir Van der Straeten et al. (2013) pour une analyse expérimentale de ce laminage.
-
[13]
Pour une analyse plus approfondie de la littérature empirique sur le vote stratégique, voir la contribution de Blais et Degan (2016) dans ce même numéro.
-
[14]
Le mode de scrutin appelé « vote alternatif », ou « vote simple transférable » ou encore « instant runoff » est utilisé dans certains pays anglo-saxons. Il peut être vu comme une extension du vote à deux tours. L’électeur soumet une liste ordonnée de ses choix. Dans un premier tour, on ne compte que les premiers choix. Le candidat le moins souvent en tête est alors éliminé et chaque vote qu’il avait attiré est alors transféré au choix suivant de l’électeur. Le processus est ensuite itéré jusqu’à ne trouver qu’un seul candidat.
Bibliographie
- Ahn, D. S. et S. Oliveros (2012), « Combinatorial Voting », Econometrica, 80(1) : 89-141.
- Ahn, D. S. et S. Oliveros (2014), « The Condorcet Jur(ies) Theorem », Journal of Economic Theory, 150 : 841-851.
- Austen-Smith, D. et J, Banks (1996), « Information Aggregation, Rationality, and the Condorcet Jury Theorem », American Political Science Review, 90 : 34-45.
- Baujard, A., F. Gavrel, H. Igersheim, J.-F. Laslier et I. Lebon (2013), « Vote par approbation, vote par note : une expérimentation lors des élections présidentielles françaises du 22 avril 2012 », Revue Economique, 64(2) : 345-356.
- Bhattacharya, S. (2013), « Preference Monotonicity and Information Aggregation in Elections », Econometrica, 81(3) : 1229-1247.
- Blais, A. (2000), To Vote or not to Vote?: The Merits and Limits of Rational Choice Theory, University of Pittsburgh Press.
- Blais, A. et A. Degan (2016), « L’étude du vote stratégique », L’Actualité économique, ce numéro.
- Blais, A., L. Massicotte et A. Dobrzynska (1997), « Direct Presidential Elections: A World Summary », Electoral Studies, 16 : 441-455.
- Blais, A., J.-B. Pilet, K. Vander Straeten, J.-F. Laslier et M. Héroux-Legault (2014), « To Vote or to Abstain? An Experimental Test of Rational Calculus in First Past the Post and PR Elections », Electoral Studies, 36 : 39-50.
- Blais, A. et R. Young (1999), « Why do People Vote? An Experiment in Rationality », Public Choice, 99(1-2) : 39-55.
- Borda, J.C. de. (1781), Mémoire sur les élections au scrutin.
- Bouton, L. (2013), « Theory of Strategic Voting in Runoff Elections », The American Economic Review, 103(4) : 1248-1288.
- Bouton, L. et M. Castanheira (2012), « One Person, Many Votes: Divided Majority and Information Aggregation », Econometrica, 80 : 43-87.
- Bouton, L., M. Castanheira et A. Llorente-Saguer (2016a), « Divided Majority and Information Aggregation: Theory and Experiment », Journal of Public Economics, 134 : 114-128.
- Bouton, L., M. Castanheira et A. Llorente-Saguer (2016b), « Multicandidate Elections: Aggregate Uncertainty in the Laboratory », Games and Economic Behavior.
- Bouton, L. et G. Gratton (2015), « Majority Runoff Elections: Strategic Voting and Duverger’s Hypothesis », Theoretical Economics, 10(2) : 283-314.
- Brams, S.J. et P. C. Fishburn (1983), Approval Voting, Birkhauser, Boston.
- Brams, S.J. et P. C. Fishburn (2005), « Going from Theory to Practice: The Mixed Success of Approval Voting », Social Choice and Welfare, 25 : 457-474.
- Brennan, G. et A. Hamlin (1998), « Expressive Voting and Electoral Equilibrium », Public Choice, 95(1-2) : 149-175.
- Campbell, D.E. et J.S. Kelly (2009), « Gains from Manipulating Social Choice Rules », Economic Theory, 40 : 349-371.
- Campbell, D.E. et J.S. Kelly (2013), « Breadth of Loss due to Manipulation », Economic Theory. DOI: 10.1007/s00199-013-0752-4.
- Castanheira, M. (2003), « Victory Margins and the Paradox of Voting », European Journal of Political Economy, 19(4) : 817-841.
- Chamberlain, G. et M. Rothschild (1981), « A Note on the Probability of Casting a Decisive Vote », Journal of Economic Theory, 25(1) : 152-162.
- Chatterji, S. et A. Sen (2011), « Tops-only Domains », Economic Theory, 46 : 255-282.
- Cox, G. W. (1994), « Strategic Voting Equilibria under the Single Nontransferable Vote », American Political Science Review : 608-621.
- Cox, G. W. (1997), Making Votes Count: Strategic Coordination in the World’s Electoral Systems, Cambridge Univ Press.
- De Sinopoli, F., B. Dutta et J.F. Laslier (2006), « Approval Voting: Three Examples », International Journal of Game Theory, 38 : 27-38.
- Dellis, A. (2010), « Weak Undominance in Scoring Rule Elections », Mathematical Social Sciences, 59(1) : 110-119.
- Dowding, K. et M. van Hees (2008), « In Praise of Manipulation », British Journal of Political Science, 38 : 1-15.
- Duverger, M. (1951), Les partis politiques. Colin.
- Endriss, U. (2013), « Sincerity and Manipulation under Approval Voting », Theory and Decision, 74 : 335-355.
- Evans, J. S. B., S. Newstead et R. MJ. Byrne (1993), Human Reasoning: The Psychology of Deduction, Psychology Press.
- Feddersen, T. (1992), « A Voting Model implying Duverger’s Law and Positive Turnout », American Journal of Political Science : 938-962.
- Feddersen, T. et W. Pesendorfer (1996), « The Swing Voter’s Curse », American Economic Review, 86 : 408-424.
- Feddersen, T. et W. Pesendorfer (1997), « Voting Behavior and Information Aggregation in Elections with Private Information », Econometrica, 65 : 1029-1058.
- Feddersen, T. et W. Pesendorfer (1998), « Convicting the Innocent: The Inferiority of Unanimous Jury Verdicts under Strategic Voting », American Political Science Review, 92 : 22-35.
- Fey, M. (1997), « Stability and Coordination in Duverger’s Law: A Formal Model of Preelection Polls and Strategic Voting », American Political Science Review, 91(01) : 135-147.
- Fiorina, M.P. (1976), « The Voting Decision: Instrumental and Expressive Aspects », The Journal of Politics, 38(02) : 390-413.
- Fisher, S. D. et D.P. Myatt (2002), « Strategic Voting Experiments », Technical report, Nuffield College politics working paper.
- Fisher, S. et M. Myatt (2014), « Strategic Voting in Plurality Rule Elections », Technical report, mimeo, London Business School.
- Forand, J.G. et V. Maheshri (2015), « A Dynamic Duverger’s Law », Public Choice, 165(3-4) : 285-306.
- Forsythe, R. R.B. Myerson, T.A. Rietz et R.J. Weber(1993), « An Experiment on Coordination in Multi-candidate Elections: The Importance of Polls and Election Histories », Social Choice and Welfare, 10(3) : 223-247.
- Goertz, J. et F. Maniquet (2011), « On the Informational Efficiency of Simple Scoring Rules », Journal of Economic Theory, 146 : 1464-1480.
- Good, I.J. et I.S. Mayer (1975), « Estimating the Efficacy of a Vote », Behavioral Science, 20(1) : 25-33.
- Green, D.P. et A.S. Gerber (2008), Get out the Vote: How to Increase Voter Turnout, Brookings Institution Press.
- Guarnaschelli, S., R.D. McKelvey et T.R. Palfrey (2000), « An Experimental Study of Jury Decision Rules », American Political Science Review, 94(02) : 407-423.
- Igersheim, H., A. Baujard et J.-F. Laslier (2016), « La question du vote. Expérimentations en laboratoire et in situ », L’Actualité économique, 92 : 151-189.
- Jackson, M.(2001), « A Crash Course in Implementation Theory », Social Choice and Welfare, 18 : 655-708.
- Kabré, A., J.-F. Laslier et L. Wantchekon (2015), « About Political Polarization in Africa: An Experiment on Approval Voting in Benin », miméo.
- Lang, J. (2015), « Le choix social à l’aide de l’électeur de gauche désemparé en région Grand Est », miméo.
- Laslier, J.F. (2009), « The Leader Rule: A Model of Strategic Approval Voting in a Large Electorate », Journal of Theoretical Politics, 21 : 113-136.
- Laslier, J-F. et M.R. Sanver (2010), Handbook on Approval Voting. Heildelberg: Springer-Verlag.
- Laslier, J-F. et K. VanderStraeten (2004), « Une expérience de vote par assentiment lors de l’élection présidentielle française de 2002 », Revue française de science politique, 54 : 99-130.
- Ledyard, J. O. (1984), « The Pure Theory of Large Two-candidate Elections », Public Choice, 44(1) : 7-41.
- Levine, D. K et T.R. Palfrey (2007), « The Paradox of Voter Participation? A Laboratory Study », American Political Science Review, 101(1) : 143-158.
- Man, P.T.Y. et S.A. Takayama (2013), « A Unifiying Impossiblity Theorem », Economic Theory, 54 : 249-271.
- Mandler, M. (2012), « The Fragility of Information Aggregation in Large Elections », Games and Economic Behavior, 74(1) : 257-268.
- Martinelli, C. (2002), « Simple Plurality versus Plurality Runoff with Privately Informed Voters », Social Choice and Welfare, 19(4) : 901-919.
- McLennan, A. (2011), « Manipulation in Elections with Uncertain Preferences », Journal of Mathematical Economics, 47 : 370-375.
- Merill, S. et J. Nagel (1987), « The Effect of Approval Balloting on Strategic Voting Under Alternative Decision Rules », American Political Science Review, 81 : 509-524.
- Myatt, D.P. (2007), « On the Theory of Strategic Voting », The Review of Economic Studies, 74(1) : 255-281.
- Myatt, D.P. (2015), « A Theory of Voter Turnout », miméo.
- Myerson, R.(1978), « Refinements of the Nash Equilibrium Concept », International Journal of Game Theory, 15 : 133-154.
- Myerson, R. (2002), « Comparison of Scoring Rules in Poisson Voting Games », Journal of Economic Theory, 103 : 219-251.
- Myerson, R. (1998a), « Extended Poisson Games and the Condorcet Jury Theorem », Games and Economic Behavior, 25 : 111-131.
- Myerson, R. (1998b), « Population Uncertainty and Poisson Games », International Journal of Game Theory, 27 : 375-392.
- Myerson, R. (2000), « Large Poisson Games », Journal of Economic Theory, 94 : 7-45.
- Myerson, R. et R.J. Weber (1993), « A Theory of Voting Equilibria », American Political Science Review, 87 : 102-114.
- Núñez, M. (2010), « Condorcet Consistency of Approval Voting: A Counter Example on Large Poisson Games », Journal of Theoretical Politics, 22 : 64-84.
- Núñez, M. (2014), « The Strategic Sincerity of Approval Voting », Economic Theory, 56(1) : 157-189.
- Núñez, M. et D. Xefteris (2015), « Electoral Thresholds as Coordination Devices », The Scandinavian Journal of Economics, 119(2) : 346-374.
- Piketty, T. (2000), « Voting as Communicating », The Review of Economic Studies, 67(1) : 169-191.
- Rietz, T., R. Myerson et R. Weber (1998), « Campaign Finance Levels as Coordinating Signals in Three-way, Experimental Elections », Economics & Politics, 10(3) : 185-218.
- Riker, W.H. (1982), « The Two-party System and Duverger’s Law: An Essay on the History of Political Science », American Political Science Review, 76(04) : 753-766.
- Riker, W.H. (1986), « Duverger’s Law Revisited », Electoral Laws and their Political Consequences : 19-42.
- Riker, W.H. et P.C. Ordeshook (1968), « A Theory of the Calculus of Voting », American Political Science Review, 62(1) : 25-42.
- Roemer, J.E. (2009), Political Competition: Theory and Applications, Harvard University Press.
- Sanver, R. (2010), « Approval as an Intrinsic Part of Preference », in Laslier, J.F. et R. Sanver (éds), Handbook on Approval Voting, Heildelberg: Springer-Verlag.
- Sauger, N., A. Blais, J.-F. Laslier et K. Vander Straeten (2012), « Strategic Voting in the Laboratory », in B. Kittel, W. Luhan, et R. Morton (éds), Experimental Political Science: Principles and Practices, Palgrave-Macmillan.
- Schram, A. et J. Sonnemans (1996), « Voter Turnout as a Participation Game: An Experimental Investigation », International Journal of Game Theory, 25(3) : 385-406.
- Schram, A. et J. Sonnemans (1996), « Why People Vote: Experimental Evidence », Journal of Economic Psychology, 17(4) : 417-442.
- Tyran, J.-R. (2004), « Voting when Money and Morals Conflict: An Experimental Test of Expressive Voting », Journal of Public Economics, 88(7) : 1645-1664.
- Vander Straeten, K., J.-F. Laslier et A, Blais (2013), « Vote au Pluriel: How People Vote when Offered to Vote under Different Rules », PS: Political Science & Politics, 46(2) : 324-328.
- Vander Straeten, K., J.-F. Laslier et A, Blais (2015), « Patterns of Strategic Voting in Run-off Elections », à paraître dans Blais, A., J.-F. Laslier et K. Vander Straeten (éds), Voting Experiments, Springer.
- Vander Straeten, K., J.-F. Laslier, N. Sauger et A. Blais, (2010), « Strategic, Sincere, and Heuristic Voting under Four Election Rules: An Experimental Study », Social Choice and Welfare, 35(3) : 435-472.
- Van Der Straeten, K., N. Sauger, J.-F. Laslier, J.-F. et A. Blais (2013), « Sorting out Mechanical and Psychological Effects in Candidate Elections: An Appraisal with Experimental Data », British Journal of Political Science, 43(04) : 937-944.
- Wolitzky, A. (2009), « Fully Sincere Voting », Games and Economic Behaviour, 67 : 720-735.


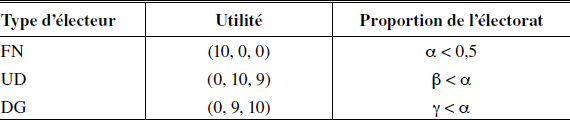


 10.7202/1039875ar
10.7202/1039875ar