Corps de l’article

Introduction

À l’instar de plusieurs autres États, le Québec a choisi d’orienter sa nouvelle réforme du système d’éducation selon une approche par compétence. Le nouveau programme de mathématiques vise ainsi, pour chacun des niveaux scolaires du primaire et du secondaire, le développement de trois compétences parmi lesquelles on retrouve « Communiquer à l’aide du langage mathématique » (Gouvernement du Québec, 2001). Ce choix curriculaire amène à s’interroger à la fois sur le rôle de la communication et du langage dans la pratique mathématique et dans son apprentissage, et sur la façon dont on peut évaluer chez un élève le degré de maîtrise de cette compétence.

Dans cet article, nous apportons quelques éléments de réponse à ces questions à partir de travaux effectués dans le cadre d’un projet visant à déterminer les effets de la formation fondamentale sur les compétences d’étudiants universitaires dans la résolution de problèmes de mathématiques appliquées (Caron, 2001). L’idée à l’origine de ce projet était d’identifier les facteurs dans l’enseignement et l’apprentissage des mathématiques qui en favorisent le transfert à des domaines d’application comme le génie, la gestion ou l’informatique. En particulier, nous nous interrogions sur la place à accorder à l’application et aux outils informatiques dans le cours de mathématiques.

Les compétences dans la résolution de problèmes

Il apparaît d’abord utile de rappeler que la notion de compétence nous vient de l’entreprise. Dans ce milieu, l’idée de compétence a en effet remplacé, depuis quelques années déjà, l’idée de « qualification » dont le caractère définitif ne permettait pas de suivre l’évolution rapide de la nature du travail (Dugué et Maillebouis, 1994). Cette évolution peut être caractérisée par une multiplication des connaissances et une complexité croissante des problèmes à résoudre, issus de contextes d’action de moins en moins structurés et portant sur des objets de plus en plus abstraits. Après avoir remplacé le « faire » par le « savoir-faire », le monde du travail valoriserait maintenant à son tour le « savoir que faire » (De Terssac, 1996) et ferait preuve d’un intérêt renouvelé pour les habiletés d’analyse, de synthèse, de communication, ainsi que pour les capacités d’apprentissage et le jugement critique (Conseil supérieur de l’éducation, 1994). Ce phénomène a sans doute favorisé la transposition en éducation de la notion de compétence, car plusieurs y ont vu une façon adéquate de décrire les enjeux de la formation fondamentale.

Privilégier les compétences, c’est inviter à établir un rapport différent aux savoirs et à se recentrer sur la formation de la pensée. L’idée de compétence dénote le souci d’initier dès l’école le développement d’habiletés complexes qui seront essentielles à l’adaptation ultérieure de l’individu à un environnement changeant. Elle suppose le développement d’outils intellectuels flexibles, aptes à s’ajuster aux transformations et à favoriser l’acquisition de nouvelles connaissances.

Gouvernement du Québec, 2001, p. 4

Dans le cadre de ses travaux en didactique des sciences, Orange (1997) présente la compétence comme un concept plus « modeste » permettant de traduire en classe les enjeux, à la fois pour la société et pour l’individu, d’une « culture scientifique » : partage d’une technicité, bien sûr, mais aussi « développement des structures mentales, des outils intellectuels, des capacités de penser qui ouvrent de nouvelles possibilités de compréhension ». À partir d’une telle définition, le concept de compétence semble tout indiqué pour étudier la capacité d’étudiants universitaires à utiliser, dans leur passage à l’application, les connaissances qu’ils ont acquises en mathématiques.

Orange (Ibid.) montre que la notion de compétence n’est utile que lorsqu’on y lie contenu et mise en oeuvre ou objets de savoir et méthodes. Il poursuit en suggérant que la mise en relation à travers la notion de compétence des contenus et de leur mise en oeuvre se définit par la « maîtrise de classes de problèmes ». Cette approche exploite le schéma circulaire qui lie de façon historique connaissances et problèmes dans un processus d’alimentation mutuelle : toute connaissance naît de la nécessité de résoudre un problème (Popper, 1991), et les nouvelles connaissances ainsi acquises modifient à leur tour le champ des problèmes.

La résolution de problèmes se retrouverait donc au coeur de l’approche par compétence, car elle apparaît à la fois comme le cadre d’observation des compétences et le mode privilégié de leur développement. C’est donc dans ce cadre que nous avons cherché à appréhender les compétences mathématiques liées à la communication et à l’utilisation des différents langages et représentations.

L’identification des compétences nécessaires à la résolution de problèmes dans un contexte particulier commande de partir des pratiques de référence (Perrenoud, 1998). Il nous a donc semblé pertinent, dans un premier temps d’analyse, de retourner du côté du milieu du travail, là où l’idée de compétence a d’abord émergé. Dans le cadre de ses recherches en sociologie du travail, De Terssac (1996) a identifié trois types de compétences qui différencient les individus et les mettent en concurrence. Nous avons cherché à projeter cette classification sur les différents modes d’utilisation du savoir mathématique :

  • Les « compétences d’explicitation » (les « savoir dire ») pour traduire ce qui est, ce qu’il y a à faire et ce qui a été fait. En mathématiques, cela implique la maîtrise d’au moins trois langages [1] différents (naturel, symbolique et graphique) (De Serres et Groleau, 1997) et du passage de l’un à l’autre par la modélisation et l’interprétation. On peut préciser cette description en accordant un statut particulier au langage numérique à l’intérieur du langage symbolique. On peut aussi y ajouter d’autres langages si l’on étend l’activité mathématique à la définition d’algorithmes (pseudo-code), la programmation (langage de programmation) et l’utilisation de logiciels de calculs (communication à l’interface).

  • Les « compétences d’évaluation » (les « savoir se situer ») pour identifier, légitimer et valider tout ce qu’on engage dans l’action. En mathématiques, cela paraît correspondre à la décomposition en sous-problèmes, à l’identification des cas possibles, à la reconnaissance des champs théoriques appropriés, à la navigation dans le réseau des concepts, à l’utilisation du raisonnement mathématique, à la vérification de propriétés, etc.

  • Les « compétences d’intervention » (les « savoir intervenir ») pour agir en mettant en situation les connaissances disponibles et en transformant les situations rencontrées en connaissances réutilisables dans d’autres contextes. Dans le contexte mathématique, cela correspond à l’utilisation des différentes méthodes (analytique et algorithmique) permettant de calculer, d’appliquer une transformation sur un objet, de résoudre un système d’équations, d’optimiser une fonction, etc., ainsi qu’à la généralisation par l’abstraction pour étendre des résultats ou l’emploi de méthodes à une classe de problèmes.

Ces trois types de compétence sont évidemment fortement liés. En particulier, les compétences d’évaluation s’appuient à la fois sur les compétences d’explicitation et d’intervention. On peut par ailleurs aisément concevoir qu’on ne puisse faire l’économie d’un des types de compétence dans la résolution d’un problème mathématique nouveau, pour lequel un algorithme menant directement de l’énoncé à la réponse n’est pas connu a priori. Il n’est donc pas surprenant de pouvoir établir des liens entre cette classification et les trois compétences visées en mathématiques par le nouveau Programme de formation de l’école québécoise (Gouvernement du Québec, 2001) et applicables du début du primaire à la fin du secondaire : les compétences d’« explicitation » correspondent à la compétence 3 « Communiquer à l’aide du langage mathématique », celles d’« évaluation » à l’essentiel de la compétence 2 « Raisonner à l’aide de concepts et de processus mathématiques », tandis que les compétences d’« intervention », souvent privilégiées dans une approche procédurale de l’enseignement des mathématiques, sont désormais réduites à une des composantes de la compétence 2 « L’élève applique des processus mathématiques appropriés à la situation ». La compétence 1 « Résoudre une situation problème mathématique » englobe toutes les autres compétences.

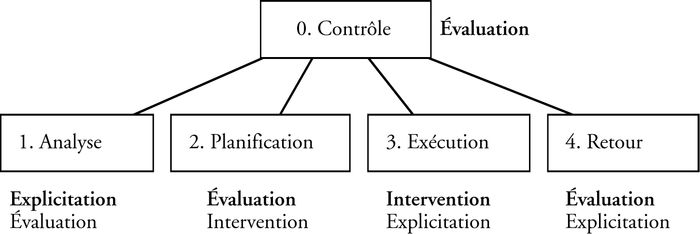
Les trois types de compétence définis par De Terssac (1996) peuvent servir à mieux caractériser les différentes phases du processus de résolution de problèmes définies par Polya (1945). En phase d’analyse, comme il s’agit essentiellement de traduire un énoncé de problème en une forme résoluble, on fait appel en premier lieu aux compétences d’explicitation pour comprendre l’objectif et les données du problème, et en deuxième lieu aux compétences d’évaluation pour identifier les concepts mathématiques qui pourraient être mis à contribution dans l’étude du problème. Les compétences d’explicitation servent aussi de soutien à la communication lors de l’exécution de la stratégie et du retour sur la solution pour interpréter et discuter les résultats. Les compétences d’évaluation jouent un rôle clé dans la planification de la résolution pour décomposer le problème et choisir les méthodes applicables, ainsi que dans le retour sur la solution pour juger de la qualité des résultats et de leur généralité. On peut aussi les associer au contrôle défini par Schoenfeld (1985), c’est-à-dire partout où il convient de prendre une décision sur la direction à prendre ou de porter un jugement sur le progrès accompli. Quant aux compétences d’intervention, elles sont les grandes responsables de la phase d’exécution pour appliquer les méthodes identifiées, mais elles sont aussi mises à contribution en phase de planification, là où la connaissance de méthodes d’intervention élargit le spectre des stratégies envisageables, ainsi qu’en phase de retour pour vérifier et généraliser les résultats. Ce modèle, associant phases et compétences, schématisé par la figure 1, nous a servi de cadre de référence dans l’étude des compétences mathématiques d’étudiants universitaires.

Figure 1

Les compétences dans la résolution de problèmes

Les compétences dans la résolution de problèmes

-> Voir la liste des figures

Méthodologie

Notre étude, de nature exploratoire, visait à clarifier les relations entre l’histoire éducative d’étudiants universitaires et leurs compétences en situation de résolution de problèmes de mathématiques appliquées. Nous avions choisi de couvrir trois domaines d’application différents : le génie, la gestion et l’informatique. Dans chacune des formations universitaires associées, nous nous sommes intéressée aux étudiants d’un cours obligatoire de première session faisant appel aux connaissances mathématiques. L’étude a été menée sur deux plans : le premier, que nous avons appelé « quantitatif », avec une quarantaine de participants volontaires et le deuxième, désigné sous le vocable « qualitatif », avec un sous-ensemble de douze participants.

L’histoire éducative des étudiants qui ont participé à l’étude a été constituée à partir de questionnaires (plan quantitatif) et d’entrevues (plan qualitatif) où nous cherchions à cerner les places respectives faites à la théorie mathématique, à l’informatique et à l’application dans la formation reçue, ainsi que les rapports qu’entretiennent ces étudiants avec ces composantes de leur formation. L’idée sous-jacente était de décortiquer les contributions respectives des savoirs théoriques et des savoirs pratiques dans le développement des compétences.

Pour pouvoir traduire en termes de compétence les productions des étudiants dans la résolution des problèmes proposés dans le cadre de leur cours, nous avons construit une grille d’analyse en associant aux différentes phases du processus de résolution de problèmes les compétences mises à contribution. Nous avons également précisé le type de compétence, soit d’évaluation, d’intervention ou d’explicitation. Pour être applicables à l’ensemble des secteurs d’application, ces compétences devaient être exprimées sous forme « générique », en reflétant les différents modes de pensée impliqués dans l’application des mathématiques et en évitant d’être liées à des contenus spécifiques (par exemple, identifier l’objectif, mettre en équations, structurer la résolution en décomposant en sous-problèmes, utiliser une fonction logicielle, valider avec des cas particuliers, etc.).

Au plan quantitatif, cette grille a servi à classer les erreurs commises par les étudiants dans la résolution de problèmes de leur cours : chacune des erreurs recensées devait être associée à la principale compétence qui semblait avoir fait défaut. Les professeurs, chargés de cours et auxiliaires d’enseignement des trois cours où s’est déroulée la collecte des données ont collaboré à la validation et à l’application de la grille. Cet exercice a permis d’intégrer une perspective didactique à l’évaluation, en attirant l’attention sur la raison de l’erreur, le caractère opératoire de la connaissance, les processus impliqués et les phénomènes récurrents. Il a aussi fait ressortir que l’évaluation des compétences n’échappe pas à une part d’interprétation en raison du caractère multiple de certaines erreurs (par exemple, une erreur en phase d’analyse peut ne pas être corrigée en phase de retour) et de la difficulté à repérer les différents processus cognitifs impliqués dans les productions des étudiants à cause d’une explicitation souvent très fragmentaire.

Participants

Quarante-trois étudiants ont accepté de participer à l’étude, étudiants qui, en janvier 2000, suivaient un cours de première session d’un programme universitaire où l’on applique les mathématiques. La formation mathématique que ces étudiants ont reçue au secondaire apparaît généralement conforme aux programmes des années 1980, définis selon une approche procédurale [2] : l’accent était mis sur les techniques de calcul avec un entraînement par les exercices, et le développement de capacités à démontrer n’était pas inclus dans la liste des objectifs visés. La formation mathématique reçue au collégial était définie en termes de contenus minimaux et non d’objectifs d’apprentissage, et se révèle, par conséquent, beaucoup plus variable dans les contenus couverts, les approches d’enseignement utilisées et le degré de formalisme impliqué. De façon générale, les applications étaient peu présentes dans le cours de mathématiques, et l’intégration d’outils technologiques s’est limitée bien souvent au maniement de la calculatrice numérique. Le tiers des participants ont été initiés à l’utilisation d’une autre approche technologique (calculatrice graphique, logiciel statistique, calculateur symbolique, etc.) dans le cadre d’un cours de mathématiques, particulièrement au collégial.

Parmi les participants sur le plan quantitatif, douze étudiants ont été choisis pour contribuer au plan qualitatif de l’étude. Ils ont été sélectionnés sur la base de leurs réponses à un questionnaire caractérisant leur formation, leurs intérêts et leurs perceptions. Pour chacun des trois secteurs d’application, nous avons cherché à constituer un échantillon représentatif, contrasté et révélateur, en visant une répartition équilibrée des quatre sujets retenus dans le plan défini par les dimensions théorique (richesse des connaissances mathématiques, place accordée à la démonstration, intérêt pour le raisonnement, etc.) et pratique (utilisation de la technologie, place accordée à l’application, expériences de travail, etc.) de la formation reçue. Ces étudiants ont été reçus en entrevue et nous avons procédé à une analyse didactique détaillée de leurs productions.

Résultats

Au plan quantitatif, les données recueillies indiquent que 70 % des erreurs des étudiants se retrouvent en phase d’analyse (37 %) ou de planification (33 %). De façon duale, les erreurs paraissent liées avant toute chose à l’évaluation (54 %), puis à l’explicitation (30 %) et, finalement, à l’intervention (16 %). Les deux erreurs les plus fréquemment observées sont des erreurs d’évaluation et ont trait à l’identification des concepts mathématiques sous-jacents ou à l’identification d’une méthode de résolution applicable : à elles seules, ces difficultés d’identification comptent pour près de 20 % des erreurs. Souvent au centre des apprentissages mathématiques au secondaire et au collégial, les manipulations algébriques ou analytiques (par exemple, calcul de dérivée) ne sont à la source que de 2 % des erreurs observées.

Au plan qualitatif, la mise en relation des stratégies d’apprentissage privilégiées avec les compétences mathématiques démontrées a fait ressortir à plusieurs reprises l’importance de l’explicitation dans le développement des compétences d’évaluation. En effet, ceux qui font montre de compétences supérieures en évaluation investissent davantage, et de façon personnelle et autonome, dans l’explicitation des contenus d’apprentissage : lecture, questionnement, argumentation, utilisation des définitions, réécriture du cours, confection de résumés, de tableaux synthèse, etc. Cette observation nous a amenée à envisager un modèle par niveaux des efforts d’explicitation mis à contribution dans l’apprentissage des mathématiques (voir figure 2). Par ce modèle, nous ne cherchons pas à réduire les mathématiques à un langage ni la pratique mathématique à l’exercice de différents langages, mais plutôt à démontrer l’importance de l’explicitation dans l’appropriation des concepts et dans l’exercice de cette pratique. Ce sont donc les différents niveaux d’explicitation que nous tâcherons de décrire et d’illustrer dans les sections qui suivent.

Figure 2

Niveaux d’explicitation dans l’apprentissage des mathématiques

Niveaux d’explicitation dans l’apprentissage des mathématiques

-> Voir la liste des figures

Niveau d’association

Au premier niveau, on retrouve l’association : on peut lire, reconnaître, mémoriser et reproduire une expression, une figure, une définition ou un énoncé. Une fois que le registre d’explicitation et l’élément qui s’y rapporte sont déterminés, on peut appliquer des méthodes d’intervention sur cet élément (par exemple, manipulations algébriques, calcul de dérivée, transformation géométrique, etc.).

Selon la plupart des étudiants rencontrés, il était tout à fait possible de très bien réussir au secondaire en se contentant de « faire ses exercices », d’étudier « ses formules » et de se limiter à un niveau d’association dans l’explicitation des contenus. « Au secondaire, ça se limitait vraiment à voir si t’étais capable d’appliquer une formule. On n’était pas aussi exigeant au niveau de la compréhension. » (Michel, étudiant aux HEC)

Ce traitement expéditif dans l’apprentissage n’était pas pour déplaire à tous : avec une vie plus chargée que jamais entre les études, la multiplication des loisirs et le travail rémunéré qui a pris depuis quelques années de nouvelles proportions, plusieurs étudiants en sont venus à considérer comme une stratégie rentable la mémorisation de la correspondance entre les énoncés des questions et les formules à appliquer, et à accorder, par conséquent, une grande importance à l’écriture symbolique des formules à mémoriser. Un étudiant nous a raconté qu’il se voyait avantagé par l’excellence de sa mémoire photographique qui lui permettait d’étudier ses formules à la toute dernière minute.

Le fait de privilégier dans l’apprentissage des mathématiques les calculs effectués au niveau symbolique mène à la situation paradoxale où plusieurs étudiants utilisent l’adjectif « concret » pour décrire les cours de mathématiques (même en l’absence de référence à toute application réelle). En revanche, certains étudiants associent l’abstraction et la théorie aux autres disciplines, qui semblent s’intéresser davantage aux capacités de conceptualisation, de modélisation et d’interprétation. « Parce qu’un cours de maths, ça va travailler directement avec les chiffres. En économie, ça va être conceptuel, abstrait, dépendant des théorèmes. » (Charles, étudiant aux HEC)

Poussée à l’extrême, cette vision amène à réduire le concept à son symbole. Ce dernier devient alors la réalité « concrète » à manipuler en appliquant les procédures prescrites. Ce phénomène n’est pas exclusif au secondaire ; nous avons pu l’observer aussi avec des concepts du collégial. En effet, il est remarquable de constater que, dans un problème de physique mécanique demandant de déterminer la hauteur d’un tremplin qui permettrait à une rondelle qui y glisserait de « parcourir la plus grande distance », aucun des participants de Polytechnique n’ait pensé à utiliser la dérivée, méthode pourtant au coeur des apprentissages mathématiques du collégial. Le peu d’importance accordée dans leur formation au sens de la dérivée, au-delà de l’application de règles de manipulation symbolique, permettrait d’expliquer ce phénomène.

Le problème d’informatique suivant a donné lieu à une autre illustration de la domination que paraît exercer le symbole au détriment du sens.

Alors que l’analyse de l’énoncé du problème aurait dû faire appréhender les variables i et j comme les limites de l’intervalle de recherche, et donc comme des paramètres dont la valeur était fixée à l’entrée de la procédure, la majorité des étudiants ont plutôt associé les symboles i et j à des compteurs, comme c’est souvent le cas tant en programmation que dans les suites et séries mathématiques.

Cette centration sur le symbolique permet, par ailleurs, d’occulter ce qu’on n’a pas compris, c’est-à-dire le sens qui pourrait se cacher derrière le langage. On peut ainsi se limiter à viser une cohérence interne, en reproduisant dans une langue étrangère une régularité qui nous a été imposée comme une loi. Avec des objectifs d’apprentissage qui constituent un contrat clair des procédures qui seront évaluées (et qu’il convient donc d’apprendre), l’approche procédurale paraît en effet dispenser de la nécessité de comprendre. Cela explique que les étudiants qui éprouvaient des difficultés de compréhension y aient adhéré fortement, car ils pouvaient se permettre de miser exclusivement sur l’entraînement et la mémorisation et obtenir de bons résultats en retour. En fait, avec une rétroaction continue grâce aux solutionnaires fournis et aux examens fréquents (formatifs et sommatifs), il n’apparaissait même pas nécessaire de se questionner sur les limites de sa compréhension. Une étudiante nous a ainsi confié qu’elle attendait les résultats de l’examen formatif pour déterminer ce qu’elle devait étudier.

Dans l’analyse des compétences d’explicitation, le symbole mathématique de l’égalité mérite une attention particulière, car il est au coeur de l’opération de modélisation. Si, lors de l’apprentissage de l’arithmétique au primaire, les élèves lui attribuent souvent un sens opératoire (« ça donne… »), on serait en droit de penser que le passage à l’algèbre, une fois complété, ait permis de lui restituer son sens original et de voir une équation pour ce qu’elle est, c’est-à-dire une égalité entre deux membres qui lient, entre elles, variables et constantes. Or il semble que l’apprentissage des mathématiques au secondaire ait eu pour effet, chez certains, de perpétuer le caractère opératoire de l’égalité, en la réduisant à un élément de liaison entre deux étapes d’une procédure, voire à un nouveau « ça donne » entre la formule et la réponse. Cette vision opératoire de l’égalité, sans doute renforcée par l’utilisation de la calculatrice et de sa touche « = », est difficilement compatible avec la conception d’un système d’équations lors de la « modélisation » d’un problème de mathématiques appliquées, car elle peut conduire à rejeter les équations faisant place à plus d’une inconnue.

Nous avons pu observer un tel comportement chez Mark, étudiant à Polytechnique. Au système d’équations qui aurait modélisé adéquatement un problème de mécanique, il a substitué un enchaînement séquentiel de formules qui, si elles s’avéraient inappropriées pour la plupart, étaient en revanche savamment agencées : le membre de gauche représentait systématiquement l’inconnue cherchée et le membre de droite utilisait exclusivement des variables dont les valeurs étaient connues ou avaient été « calculées » grâce à une des formules précédentes. Dans sa modélisation du système donné, il a ainsi fait suivre une formule qui supposait une accélération nulle par une autre formule qui l’a amené à calculer une valeur non nulle pour cette accélération, et ce, sans se questionner sur la valeur d’une telle démarche. « Moi, ce que j’aime, c’est quand on a appris toutes les formules et qu’on fasse un problème synthèse, qu’on essaye de mélanger ça, de chercher comment appliquer les formules dans le bon ordre. » (Mark, étudiant à Polytechnique)

Pour les étudiants qui se situent à un niveau d’association dans l’explicitation de leurs connaissances, l’utilisation des différents langages (symbolique, numérique, graphique et naturel) et le passage de l’un à l’autre ne garantissent pas l’émergence du concept à partir de la mise en relation de ses différentes représentations. En effet, ils se limitent bien souvent à mémoriser les associations entre ces représentations sans chercher à en comprendre la raison.

Ainsi, une intégration primaire d’outils technologiques en classe de mathématiques où l’on se contente d’observer les représentations graphiques de fonctions ou de transformations algébriques ne contribue pas nécessairement à la compréhension des concepts représentés. Sans un questionnement approfondi, toute la conceptualisation requise par l’activité de traduction entre une expression symbolique et sa représentation graphique peut être laissée entièrement à la charge du logiciel ou de la calculatrice graphique. Même si ensuite on retient momentanément la correspondance observée entre les formes symbolique et graphique, cela ne veut pas dire qu’on en ait dégagé le sens. De fait, certains étudiants identifient la rapidité du traitement informatique pour tracer des graphiques comme un obstacle à la compréhension, car elle ne leur laisse pas le temps d’observer « point par point », de chercher à comprendre les phénomènes sous-jacents et d’inférer pour l’ensemble de la fonction. D’autres vont jusqu’à conclure que la facilité avec laquelle on peut produire un graphique par ordinateur dispense de se questionner sur le comportement de la fonction.

Par ailleurs, l’utilisation d’un outil informatique introduit un nouveau registre d’explicitation qui, en raison de ses exigences de rigueur et de l’impossibilité d’utiliser une part d’implicite, peut accaparer toute l’attention des étudiants dans les activités proposées et reléguer la conceptualisation mathématique au second plan. Chez ceux qui ne sont pas à l’aise avec l’outil utilisé, on constate en effet un déplacement de l’activité d’explicitation : du plan symbolico-graphique (où l’on espérait favoriser l’établissement de liens) à l’interface-usager où il convient de déterminer les commandes à entrer pour définir l’objet mathématique et agir ensuite sur sa représentation graphique. Il en résulte que ces étudiants ne retiennent pas tant les propriétés d’un concept résultant d’une synthèse de différentes représentations qu’un ensemble flou de procédures et de leurs effets, demeurant ainsi à un niveau d’association de très courte rétention.

Je me rappelle plus c’était quoi, mais je me souviens qu’on mettait une suite de commandes puis à la fin, on avait un graphique qui apparaissait. Puis après, quand on changeait les commandes, le graphique, il tournait ou c’était une autre forme […]. Mais je me rappelle plus c’était quoi. (Helga, étudiante à Polytechnique)

Le risque d’une centration momentanée, dans le cours de mathématiques, sur le registre d’explicitation du logiciel n’apparaît recevable que dans la mesure où les compétences d’explicitation informatique ainsi développées seront réutilisables et transférables à la résolution de nouveaux problèmes, possiblement plus complexes. Cette prise de position amène à privilégier, dans les approches d’intégration des technologies, une exposition prolongée à un nombre relativement limité de logiciels outils « passe-partout » qui, tout en favorisant la compréhension par la visualisation des concepts mathématiques, permettent, à plus long terme, d’étendre les capacités d’intervention et, par conséquent, le champ des problèmes résolubles. Elle ne dispense pas toutefois de chercher à comprendre les mécanismes internes de ces outils pour en débusquer les limites et porter le regard critique qui s’impose sur les résultats qu’ils peuvent produire.

Niveau de compréhension

Le recours à la langue naturelle dans l’utilisation des définitions, dans l’expression des problèmes et des solutions attendues est une première façon d’aller au-delà des nombres et des symboles qui peuvent faire obstacle non seulement à l’attribution d’un sens des concepts, mais aussi à la capacité de porter un jugement sur ce que l’on a compris.

Quand est-ce que je sais que j’ai compris ? Quand j’arrive à répondre à une question, pas une grosse question avec plein de chiffres dedans où tu peux te mélanger avec les chiffres, une question juste comme pour dire l’essentiel, en une ligne. Juste pour dire que si tu raisonnes correctement, ça veut dire que t’as compris. (Alexandre, étudiant à Polytechnique)

Mais pour espérer atteindre une précision mathématique avec la langue naturelle, il faut redoubler de rigueur dans le choix du vocabulaire et de la syntaxe. Sur ce plan, force est de constater que l’approche procédurale n’a pas toujours accordé une grande importance au vocabulaire mathématique et aux définitions, leur préférant les symboles et les formules qui combinent économie dans la forme, efficacité dans l’exécution d’exercices et non-ambiguïté dans l’évaluation et la rétroaction. On peut d’ailleurs en observer les effets chez les étudiants : certains d’entre eux (typiques du niveau d’association) définissent un concept en faisant appel directement à la formule qui permet de lui associer une valeur, privilégiant ainsi non seulement le symbolique à la langue naturelle, mais aussi le processus à l’objet (Sfard, 1991). D’autres confondent les termes de concepts connexes (par exemple, « fonctions » et « équations » ou « chiffres » et « nombres ») et donc peuvent difficilement circonscrire ces différents concepts et exploiter les liens qui les unissent.

Par ailleurs, la responsabilité de problèmes liés à l’utilisation de la langue naturelle ne peut incomber entièrement à l’apprentissage des mathématiques. Parmi les douze participants au plan qualitatif, les cinq étudiants qui commettent le plus d’erreurs d’explicitation dans l’analyse des problèmes à résoudre ont connu aussi des difficultés dans leurs cours de français, notamment au collégial où ils étaient confrontés à une nouvelle rigueur dans l’usage des mots. Certains d’entre eux reconnaissent ne pas aimer lire.

J’aime pas ça lire. J’aime ça m’attaquer directement aux problèmes, puis ça, c’est pas… faut pas vraiment faire ça. Faut vraiment lire la théorie parce que le prof, elle fait juste tirer les grandes lignes. Faut vraiment lire, comprendre les exemples, puis après faire les exercices. Ça, ça cause un problème, faut que je m’habitue à lire plus. (Helga, étudiante à Polytechnique)

À l’opposé, les trois étudiantes du groupe qui se sont distinguées par leurs compétences d’explicitation témoignent d’un rapport tout à fait différent avec le français. Partageant au départ un intérêt marqué pour la lecture, elles ont particulièrement apprécié leur passage au collégial, car il leur permettait enfin de découvrir, à travers l’analyse, le sens et, par conséquent, le plaisir de la littérature, au lieu de se cantonner à chercher « la bonne réponse », comme c’était souvent le cas au secondaire [3]. Il n’est donc pas surprenant de voir ces étudiantes accorder aujourd’hui une grande importance à connaître et à comprendre les définitions dans leurs cours de mathématiques.

L’utilisation du langage graphique constitue une autre façon de retrouver le sens derrière la forme, tout en demeurant à l’intérieur du domaine mathématique. Sur ce plan, les outils informatiques offrent un potentiel intéressant (Tall, 1992), car ils permettent un passage rapide entre les différentes représentations : symbolique, numérique, graphique. Mais pour aller au-delà de la simple association, un certain questionnement s’avère nécessaire : d’abord sur la valeur de ce qui est affiché à l’écran, compte tenu des processus internes à l’outil informatique qui peuvent engendrer des erreurs dans l’illustration des concepts mathématiques (troncature, discrétisation des variables, représentation par pixels, méthodes itératives, etc.), et ensuite sur les raisons qui font que des relations paraissent émerger entre les différentes représentations affichées.

L’utilité perçue de ces relations peut aider à engager de façon autonome un tel questionnement. Ainsi, certains étudiants disent avoir apprécié le fait de pouvoir voir par le graphique et le calcul d’aire sous la courbe l’utilité de l’intégrale, ce qui les aurait amenés à chercher à mieux comprendre le concept.

Cette idée d’utilité est aussi présente lorsqu’on lie les concepts mathématiques à leurs applications. L’application permet en effet d’attacher une nouvelle image au concept, de voir « à quoi ressemble » l’objet enseigné. Pour plusieurs étudiants, cette image n’apparaît pas toujours disponible à l’intérieur du domaine mathématique. L’utilisation de l’application peut aussi inviter à une validation autonome en permettant de juger du réalisme d’une réponse obtenue : en mathématiques financières, notamment, certains étudiants disent faire preuve d’un regard critique selon l’ordre de grandeur ou le signe de la réponse qu’ils obtiennent. Mais cela demande d’abord de se dégager des habitudes développées dans un apprentissage procédural des mathématiques où, selon une étudiante, « on arrête toujours à la réponse ». Et de plus, pour être en mesure de valider selon le sens des variables, il faut une certaine expérience de l’application en question.

De fait, l’utilisation de l’application ne paraît contribuer à la compréhension des concepts mathématiques que chez les étudiants qui manifestent un intérêt ou, tout au moins, une curiosité à l’endroit du domaine d’application présenté. Par surcroît, elle fait appel à des compétences d’explicitation supérieures. En effet, le symbole doit perdre le statut « concret » qu’on a pu lui octroyer, comme réalité propre sur laquelle on se satisfaisait de travailler, pour redevenir une représentation d’un concept abstrait, lui-même abstraction possible de réalités concrètes. Pour sa part, la compréhension de ces réalités concrètes dans toute leur complexité peut nécessiter un investissement non négligeable en lecture. Cette exigence et les niveaux multiples de traduction qui découlent d’une activité de modélisation découragent fortement ceux qui n’aiment pas lire ou qui disent aimer les mathématiques « parce qu’il y a moins de choses à comprendre »…

Cela est d’autant plus vrai que l’application des concepts mathématiques pour résoudre des problèmes issus d’une autre discipline amène à faire intervenir des écrits et un langage propres à cette discipline. À titre d’exemple, dans une discipline comme la mécanique, on accorde une grande importance au réalisme de la représentation graphique des corps impliqués ; importance tout à fait justifiée puisque c’est ainsi que les problèmes se présentent. Cette représentation peut, du moins temporairement, faire obstacle à la notion de modèle, car elle peut masquer des éléments importants et mettre en valeur des éléments accessoires. Une étape importante consiste donc à extraire les éléments essentiels en mettant à contribution à la fois les principes physiques et la géométrie de l’ensemble. Cette étape représente une difficulté non négligeable si l’on se fie aux productions des dix étudiants de Polytechnique pour le problème suivant.

Figure 3

Mécanisme engrenage-crémaillère

Mécanisme engrenage-crémaillère

-> Voir la liste des figures

Parmi les participants qui ont cherché le point de contact entre l’engrenage et la crémaillère, essentiel à la résolution du problème, aucun ne l’a situé correctement en C ; on lui a préféré le point D (voir figure 4). Ici, il est clair que la figure 3 donnée dans l’énoncé du problème privilégie le réalisme à la pureté géométrique à laquelle l’enseignement des mathématiques a pu habituer. Le contact entre l’engrenage et la crémaillère ne paraît pas, en raison des dents associées à ces objets, se limiter à un seul point. Dans ces conditions, il peut être tentant de choisir D comme point de contact, car il permet de travailler avec le triangle rectangle suggéré par la figure initiale. Ce problème illustre bien la nécessité d’un certain niveau d’abstraction dans la phase d’analyse pour réussir le passage du dessin technique au modèle géométrique apte à guider la résolution.

Figure 4

Identification du point de contact

Identification du point de contact

-> Voir la liste des figures

Du côté de la langue naturelle, l’application ou l’apprentissage d’une nouvelle discipline peut aussi attribuer un sens différent à un terme rencontré initialement en mathématiques. Par exemple, l’« équation » en chimie a un tout autre sens qu’en mathématiques (De Serres, 2000) ; l’équation chimique serait, en fait, plus près de la vision qu’ont les étudiants de la formule mathématique (elle-même très loin de la formule chimique), car elle représente une transformation possible, un traitement applicable et non une égalité. Cette polysémie du terme pourrait même renforcer certains biais conceptuels en permettant à l’étudiant, lors du passage au niveau symbolique, de repérer le « résultat » d’une équation, d’associer fortement la petite flèche au signe d’égalité et de perpétuer ainsi le caractère opératoire de ce dernier.

En résumé, la compréhension du sens d’un concept mathématique fait nécessairement appel à l’identification de liens. Ces liens peuvent demeurer à l’intérieur du domaine mathématique avec l’exploitation des définitions et la conjonction des différentes représentations. Ils peuvent aussi, par des applications, mener à l’extérieur de ce domaine. Cette deuxième approche apparaît plus exigeante sur le plan de l’explicitation, mais si l’on prend soin d’offrir un éventail varié de contextes d’application de façon à rejoindre les intérêts de chacun, elle peut constituer une source de motivation importante et favoriser le développement de compétences de modélisation, d’interprétation et de validation.

Niveau de structuration

Au troisième niveau, la structuration, on cherche à organiser et, éventuellement, à synthétiser les concepts en fonction de leur généralité et de la nature des relations qui les lient (équivalence, ordre, hiérarchie, causalité, etc.). Le développement à ce niveau est favorisé par une valorisation de la pensée déductive, car celle-ci, tout en conduisant au mode d’argumentation accepté en mathématiques, fournit le moyen de retrouver des propriétés qu’on n’est donc plus tenu de mémoriser.

La démonstration constitue la forme achevée dans l’explicitation du raisonnement déductif admis par la communauté mathématique ; elle vise à refléter et à assurer la cohérence interne de ce champ de connaissance. Mais quand ce champ est découpé en petits éléments de connaissance formulés de façon à les faire paraître presque indépendants les uns des autres, comme c’était le cas avec l’approche procédurale, la nécessité d’assurer une telle cohérence paraît s’évanouir. De fait, les programmes du secondaire n’encourageaient pas particulièrement le recours à la démonstration dans l’enseignement, et l’on y proclamait haut et fort que « Rendre l’élève capable de démontrer des théorèmes n’est pas un objectif visé par ce programme » (Gouvernement du Québec, 1992).

Si certains étudiants ont quand même eu à rédiger quelques preuves au secondaire, l’expérience était souvent circonscrite dans le temps et limitée à un module spécifique (géométrie ou logique). Elle était donc vécue comme une discontinuité ponctuelle dans l’apprentissage des mathématiques, d’un niveau de difficulté auquel on n’avait pas été habitué. Pour plusieurs, le collégial a constitué le premier contexte où la preuve était régulièrement présente, mais cela ne signifie pas pour autant qu’elle ait été présente dans tous les cours de mathématiques ni que tous les étudiants aient eu à en rédiger.

Chez certains étudiants universitaires, le niveau de formalisme qui caractérise la démonstration constitue en soi un obstacle ; pour eux, comprendre une preuve, c’est d’abord être en mesure de la traduire en ses mots. Cet exercice ne les amène pas nécessairement à en comprendre la structure : certains « détails », qui garantissent pourtant la rigueur du raisonnement, leur paraissent superflus. Ils peuvent raconter ou même mémoriser le « récit » de la preuve, mais ne saisissent pas toujours le sens de l’argumentation. Cette difficulté se manifeste clairement lorsque vient leur tour de rédiger une démonstration, comme c’est souvent le cas dans les cours d’informatique théorique de niveau universitaire. Ils avouent ne pas savoir par où commencer ni même savoir si leur preuve est valable, car la démonstration, dans les ramifications logiques de son explicitation, échappe à la définition de « réponse » qu’ils associent normalement aux exercices mathématiques : un nombre ou une expression symbolique compacte, « égal » à la variable qu’on cherchait et qu’il est possible de comparer à la « vraie réponse », donnée à la fin du manuel.

Par ailleurs, le peu de place accordée à l’apprentissage de la logique formelle conduit les étudiants à un manque de rigueur dans l’interprétation et l’utilisation des connecteurs logiques (et, ou, non, si… alors, si et seulement si). Au sens strict de ces connecteurs en mathématiques, plusieurs étudiants substituent un sens qui reflète l’utilisation polysémique qu’on peut en faire dans le langage courant. Ainsi, lorsque confrontés au pas d’induction dans une preuve par récurrence, c’est-à-dire le fameux « si P(k) alors P(k+1) », ces étudiants n’essaient pas de vérifier l’implication logique, c’est-à-dire de prouver qu’on a toujours P(k+1) lorsqu’on a P(k). Ils appliquent plutôt un traitement, comme P(k) est vrai (puisqu’ils l’ont posé ainsi), ils ont alors le « droit » d’appliquer la fonction P pour la variable k+1. Pris dans cette logique dont ils sont les premiers à percevoir l’absurdité, ils se sentent alors bien obligés de conclure que P(k+1) est vrai. Cette interprétation du « si… alors », à laquelle on est exposé très jeune dans le discours quotidien, « Si tu fais ceci, alors tu pourras faire cela… », est assez proche de l’énoncé conditionnel qu’on retrouve en programmation informatique. Toutefois, elle ne correspond pas au sens de l’implication logique en mathématiques. Dans une démonstration, on cherche à décrire un état (conclusion) à partir d’un postulat (hypothèse), alors qu’en programmation, on cherche plutôt à appliquer un traitement (donc à modifier un état) à partir de la vérification d’une condition. Il y aurait sans doute lieu de préciser ces différences sémantiques lorsqu’on enseigne à démontrer à des étudiants qui ont d’abord appris à programmer.

À l’autre extrémité du spectre des compétences d’explicitation formelle, Zoé, une étudiante en informatique, s’est particulièrement distinguée par sa capacité à rédiger des démonstrations rigoureuses. À l’origine de son intérêt pour l’abstraction, le raisonnement et la rigueur, on retrouve chez elle une difficulté à mémoriser, difficulté qui s’était manifestée dès les apprentissages arithmétiques du primaire. Contrairement à plusieurs étudiants, qui limitent la recherche de structure dans leurs cours à la classification des problèmes selon la procédure à appliquer, elle préfère procéder à un travail de structuration sur le plan des concepts pour minimiser ce qu’elle aura à mémoriser. Mais cela lui demande un travail non négligeable de réécriture de ses notes, car, dit-elle, le cours est rarement organisé en ce sens et, pour y arriver, elle procède par analogie et par déduction.

Écoute, les cours, je prenais des notes, puis après, faut que je fasse une synthèse de tout ça, puis que je mette en concepts de […] comment je pense. Tu sais, c’est quand même un travail qui demande un petit peu d’efforts […]. Tout remettre ça en forme, ça fait des résumés quand même assez condensés, puis là j’étudie ça, puis je sais tout. […] Trouver c’est quoi la notion la plus importante de toutes… de laquelle toutes les autres découlent […] ou si on peut faire des analogies […] tu te rappelles de comment c’est organisé, tu te rappelles d’une organisation plus que des choses, là. Des choses, là, tu sais, une liste de choses, comment tu peux retenir ça ? (Zoé, étudiante en informatique)

Il y a chez Zoé une illustration très forte de l’idée d’économie cognitive (Sternberg et Smith, 1988) concernant la factorisation des concepts. Ce travail l’a amenée à développer, de façon presque autonome, une pensée déductive formelle et à valoriser, par conséquent, les définitions qu’elle utilise comme points d’appui, comme « instruments pour raisonner », dirait Rouche (1987). La recherche d’une structure liant les différents concepts l’amène ainsi à approfondir le sens de ces concepts pour dégager les liens qui les unissent et donc à procéder, en premier lieu, à un travail de compréhension directement à l’intérieur du domaine mathématique, en s’aidant des définitions et d’analogies au besoin. Sa volonté de comprendre et de structurer l’amène à une plus grande autonomie dans la validation. Elle ne dépend pas du solutionnaire pour juger de la valeur de son raisonnement, particulièrement dans la rédaction de preuves. « J’ai les définitions en tête. Quand on peut s’appuyer sur les définitions puis quand nos raisonnements découlent directement des définitions, c’est certain que c’est bon. » (Zoé, étudiante en informatique)

Pour bien des étudiants qui ne voyaient pas de problèmes à mémoriser dans un cadre procédural d’apprentissage, il n’y avait pas de motivation à procéder à une telle structuration des concepts. Ce besoin a pu toutefois émerger plus tard, devant la complexité accrue des problèmes. Car les difficultés d’évaluation des étudiants dans l’élaboration de stratégies ne se manifestent pas que dans le contexte où ils ont à rédiger une démonstration ; elles peuvent aussi surgir dès que le problème ne peut être associé immédiatement à une procédure de résolution connue. Pour s’y retrouver, certains tentent de structurer sur le plan de la forme des problèmes plutôt que sur le plan des concepts ou des principes sous-jacents, perpétuant un niveau d’association dans leur explicitation. Mais cet apprentissage en surface est tôt ou tard condamné par le grand nombre de cas de figures à considérer, comme c’est souvent le cas avec l’application.

Il devient alors essentiel de pouvoir juger de la portée d’un concept pour décider s’il peut être d’un secours pour modéliser et résoudre les nouveaux problèmes. Le questionnement et l’argumentation sont alors d’un grand secours.

Je fais pas tous les exercices, mais j’essaie de comprendre. Peut-être parce que je suis structuré. […] Je pose pas mal de questions au prof. Je pense c’est ça qui aide aussi. (Alexandre, étudiant à Polytechnique)

Ça m’a pris vingt ans, je pense, à comprendre le principe. Dans le fond, c’est que quand tu vas à l’école, tu devrais pas tout accepter, tu devrais faire l’inverse : tu rejettes tout, puis après, tu comprends pourquoi, tu l’acceptes. […] Je vais le faire aussi avec mes amis. Normalement, on va être trente à s’obstiner, puis après ça on va comprendre, puis après ça on va dire au prof : « Excusez-moi, est-ce que c’est correct si on dit que ça et ça […]. » Puis là, il va nous corriger. (Charles, étudiant aux HEC)

Un intérêt nouveau pour la compréhension des conditions d’application des théorèmes, et donc du rôle de ces conditions dans la validité des théorèmes, peut alors faire surface chez certains étudiants dans le développement de leur rapport à l’application. Ces derniers, éventuellement, reconnaissent à la démonstration une utilité pour développer le raisonnement et mener à un choix éclairé dans la résolution de problèmes.

Au lieu de faire comprendre le théorème, vraiment, puis comprendre la preuve qu’il y a derrière, comme je pense qu’ils devraient faire, c’est « ok, t’as cette formule-là, applique-moi-la jusqu’à temps que tu la comprennes, tu sais, comme, pratique-la ». C’est pas bon ça, parce que tu te souviens pas de toute façon après. Si tu comprends vraiment la logique qu’il y a derrière un problème, c’est beaucoup plus intéressant. (François, étudiant en informatique)

Niveau de reformulation

Si on cherche spontanément à redéfinir, selon les structures dégagées des concepts appris, les apprentissages connexes et les nouveaux problèmes à résoudre, nous dirons qu’il y a passage au dernier niveau, celui de la reformulation, qui amènera, selon le cas, à un transfert efficace des connaissances ou à un conflit et à une révision en conséquence des structures qui semblent poser problème.

Nous avons pu observer des traces d’un tel passage chez Zoé qui, en dépit d’une expérience en programmation inférieure à la moyenne des étudiants en informatique, s’est démarquée du groupe dans l’identification des éléments nécessaires et suffisants à la conception d’algorithmes efficaces. À titre d’exemple, pour le problème de la recherche dans une suite dont nous avons reproduit l’énoncé, elle a été la seule parmi les participants à explorer cette suite dans l’ordre décroissant des indices, incorporant de façon spontanée et intuitive des considérations d’efficacité, avant même d’acquérir des notions formelles d’algorithmique. Elle paraît ainsi pouvoir faire bénéficier la structuration de ses programmes de son intérêt marqué pour les structures logico-mathématiques.

Conclusion

Ce modèle par niveau des compétences d’explicitation semble en accord avec les études qui reconnaissent aux experts la capacité d’aborder la résolution d’un problème en l’analysant en fonction de sa structure profonde plutôt qu’à partir de ses caractéristiques de surface (Chi, Feltovich et Glaser, 1981). Il permet, par ailleurs, d’expliquer les difficultés qu’éprouvent certains étudiants universitaires à juger, à prouver ou à aborder et à résoudre de nouveaux problèmes dans leur domaine d’étude : en cherchant à mémoriser des formules, à reconnaître des énoncés de problèmes pour identifier la méthode à appliquer et en se fiant exclusivement aux réponses fournies pour valider leur approche, ils essaient de développer des compétences d’intervention en travaillant presque exclusivement à un niveau d’association dans l’explicitation, en négligeant le niveau de compréhension et en structurant en fonction de la forme. Une telle stratégie d’apprentissage est exigeante sur le plan de la mémorisation et peu efficiente. En l’encourageant dans la formation, on court le risque d’éliminer d’emblée plusieurs élèves qui ne voient pas le sens d’une telle entreprise ou qui ont du mal à mémoriser. Par ailleurs, ceux qui apprennent ainsi n’apparaissent pas outillés pour analyser, modéliser, évaluer, décider et contrôler ; leurs lacunes se manifestent dès qu’ils ont à faire face à des problèmes plus complexes, qu’ils relèvent de la théorie ou de l’application.

Il ne faudrait pas voir les différents niveaux de ce modèle comme des stades à respecter dans l’apprentissage. Nous croyons au contraire que la formation générale en mathématiques devrait viser à tout moment la compréhension et la structuration des concepts chez l’élève, car l’étude tend à montrer que le fait d’entretenir, pendant une période prolongée, un apprentissage par association peut handicaper fortement, chez certains étudiants, le passage aux ordres supérieurs. Sur ce plan, les nouveaux programmes du primaire et du secondaire, du moins dans leur intention de développer de véritables compétences mathématiques, paraissent rejoindre ces objectifs. Mais pour favoriser la réalisation de ces objectifs, il faudra sans doute revoir les pratiques d’évaluation, en élargissant la part d’explicitation laissée à l’élève, en acceptant une part d’interprétation dans l’évaluation des compétences, et en redonnant à l’enseignant le droit et le devoir d’exercer son jugement professionnel.