Répartition de l’actif d’un portefeuille d’actions internationales et exposition au risque de change

Résumé

Cet article présente un cadre d’analyse général du problème double de la décision de répartition de l’actif d’un portefeuille d’actions internationales à travers les marchés boursiers et de la décision d’exposition au risque de change selon que ces décisions sont déterminées de façon passive ou font l’objet d’une optimisation. Quatre approches possibles sont examinées en se basant sur les données historiques des indices boursiers Morgan Stanley Capital International du G-7 de juillet 1976 à juin 2001. La performance relative de chacune des approches est comparée a posteriori. Dans le cas des stratégies d’optimisa­tion, l’accent est mis sur le gain marginal obtenu par le relâchement des contraintes pratiques relatives aux marchés boursiers (importance de l’écart par rapport à la capitalisation relative de l’indice boursier) et/ou aux devises (couverture du risque de change, couverture croisée, exposition au risque de change).

Abstract

This study presents a general analytical framework for the double decision of country allocation and currency risk exposure. As each of these decisions can be taken in a passive way or in an active way via optimizations, four possible approaches are scrutinized. We use Morgan Stanley Capital International historical index returns for the G-7 countries from July 1976 to June 2001 and compare the relative performance of each approach on an ex post basis. For optimisation based strategies, we focus on the marginal gain of relaxing practical constraints relative to the market indexes (importance of the tilt relative to the market capitalization of the benchmark) and/or the currencies (hedging of the currency risk, cross-hedging, exposure to the currency risk).

Introduction

La décision de répartition de l’actif d’un portefeuille est la première étape et la plus importante dans le processus de gestion de portefeuille. Brinson, Hood et Beebower (1986) et Brinson, Singer et Beebower (1991) concluent que cette décision expliquerait plus de 90 % de la variation du rendement total d’un portefeuille[1]. Malgré cette conclusion, relativement peu de temps est alloué dans les faits à la détermination de la politique de placement et de la répartition d’actif qui en découle comparativement à la gestion active du portefeuille, à savoir l’allocation tactique ainsi que l’exercice de sélection de titres. De la même façon, pour un portefeuille international, le choix d’une politique de référence en matière d’exposition au risque de change aura des répercussions majeures sur l’ensemble du processus d’investissement.

Les gestionnaires d’un portefeuille d’actions internationales pourront adopter une politique de répartition de l’actif passive, c’est-à-dire choisir la pondération de chaque marché boursier en fonction du poids dans l’indice mondial ou à l’inverse, s’écarter des poids de l’indice mondial sur la base des poids obtenus via une optimisation. La répartition internationale de l’actif peut se faire non seulement sur la base des pays, mais aussi sur la base des secteurs. Hopkins et Miller[2] (2001) montrent qu’en raison de la globalisation croissante des marchés, les effets sectoriels deviennent aussi importants que les effets pays vers la fin des années quatre-vingt-dix. Toutefois, Heston et Rouwenhorst (1994, 1995), Griffin et Karolyi (1998) ainsi que Rouwenhorst (1999) montrent qu’en moyenne, l’effet pays a été plus important que l’effet secteur durant la période 1975-1998. Dans la mesure où la dimension pays était durant cette période la plus susceptible d’ajouter de la valeur à un portefeuille d’actions internationales, il aurait donc été intéressant d’optimiser le portefeuille selon cette dimension.

Qui dit diversification internationale dit aussi risque de change! De la même façon que pour la décision de répartition de l’actif, les responsables du portefeuille d’actions internationales pourront adopter une politique de couverture passive. Il n’existe pas encore à ce jour de consensus quant au ratio de couverture à privilégier. Perold et Schulman (1988) ont été les premiers à proposer une couverture complète des investissements étrangers qui aurait l’avantage de réduire considérablement le risque à un coût très faible et correspondrait en ce sens à un free lunch[3]. À l’opposé, Froot (1993) suggère de ne pas couvrir les investissements étrangers, puisque le risque de change ne diminue pas vraiment sur un horizon de long terme[4]. Entre ces deux pôles, Gastineau (1995) propose un ratio de couverture médian (compromis) de 50 % et Black (1989, 1995) propose un ratio optimal de l’ordre de 75 %. À l’inverse, Reinert (2000) affirme qu’une stratégie de couverture active domine invariablement une stratégie de non-couverture et de couverture complète pour un portefeuille contenant plus de 10 % en actifs étrangers. Glen et Jorion (1993) ainsi que Jorion (1994) concluent que les stratégies intégrant simultanément les deux décisions de répartition des positions dans les marchés boursiers et les devises (optimisation conjointe) sont clairement supé­rieures à celles ne tenant pas compte de l’interdépendance entre les rendements des marchés boursiers et des devises (optimisation partielle ou séparée).

Cet article examine, du point de vue d’un investisseur américain, quatre approches selon que la décision de répartition de l’actif d’un portefeuille d’actions internationales à travers les marchés boursiers et la décision d’exposition au risque de change sont déterminées de façon passive ou font l’objet d’une optimisation. L’étude porte sur les indices boursiers Morgan Stanley Capital International (MSCI) des pays du G-7 et couvre la période de juillet 1976 à juin 2001. Le premier objectif de cette étude est d’examiner a posteriori l’amélioration relative de la performance d’un portefeuille international ayant adopté une des quatre approches présentées. Pour les positions résultant d’une optimisation, le second objectif de ce travail est d’offrir un cadre d’analyse reflétant les contraintes auxquelles les gestionnaires d’actions internationales et de devises peuvent être soumis et d’en analyser l’incidence sur la performance relative des portefeuilles. À la différence de Jorion (1994) et de Clarke et Kritzman (1996), nous imposons des contraintes d’optimisation réalistes ayant trait à l’importance de l’écart entre la pondération adoptée et la pondération de l’indice boursier dans le G-7. Dans le cas des devises, des contraintes relatives à la couverture du risque de change, à la couverture croisée et à l’exposition au risque de change sont examinées.

Il ressort que comparativement à la gestion passive, l’optimisation a posteriori sur les marchés boursiers et/ou les contrats à terme sur devises aurait permis d’améliorer la performance d’un portefeuille d’actions internationales. Cette performance s’améliore sensiblement avec le relâchement des contraintes, notamment celles portant sur les positions en contrats à terme sur devises. Compte tenu de ces résultats sur les données historiques, l’application de cette démarche de façon prospective, c’est-à-dire sur la base des prévisions de rendement, risque et corrélations, est prometteuse. Les procédures d’optimisation basées sur des prévisions permettraient potentiellement d’ajouter de la valeur par rapport à une répartition d’actif plus arbitraire, mais l’amélioration relative de la performance des répartitions optimales sera alors conjointement liée à la justesse des estimations.

L’étude est structurée comme suit : les données utilisées et les statistiques descriptives sont présentées dans la première partie; la seconde partie présente les quatre approches retenues ainsi qu’une comparaison des résultats obtenus; la troisième partie détaille les contraintes examinées et les résultats correspondants dans le cadre d’une optimisation conjointe; enfin, les principaux résultats sont repris dans la conclusion.

1. Données utilisées et statistiques descriptives

Nous utilisons les indices boursiers Morgan Stanley Capital International (MSCI) représentant le rendement total (incluant le dividende brut) mensuel des marchés du G-7, à savoir les États-Unis, le Canada, le Japon, le Royaume-Uni, l’Allemagne, la France ainsi que l’Italie. Les pondérations utilisées sont celles relatives à la capitalisation boursière en dollars américains de chacun des indices MSCI. Les données sur les taux de change au comptant et à terme (forward 1 mois)[5] des six devises exprimées en dollars américains proviennent de la base de données Data Resources Incorporated (DRI)[6]. Toutes les données couvrent la période allant du mois de juillet 1976 à juin 2001.

1.1 Statistiques descriptives

1.1.1 Marchés boursiers

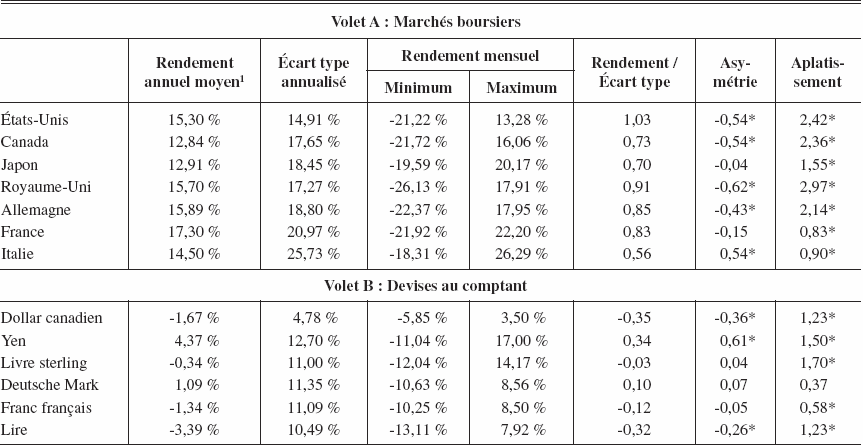
Le volet A du tableau 1 présente les principales statistiques descriptives des rendements couverts en dollars américains des sept indices boursiers. Le rendement le plus important a été réalisé sur le marché français avec une moyenne annuelle de 17,30 %; le marché canadien a connu le pire rendement avec 12,84 % par année en moyenne. Le marché américain a été le moins volatil avec un écart type annualisé de 14,91 %, le plus risqué ayant été l’Italie avec un écart type de 25,73 % (ses rendements mensuels ont oscillé d’un minimum de -18,31 % à un maximum de 26,29 %). En termes de performance globale, le marché américain a été le plus performant avec un rendement par unité de risque de 1,03, alors que l’Italie a obtenu la pire performance avec un ratio de 0,56. Les distributions de rendements présentent toutes, à l’exception de l’Italie, une asymétrie (skewness) négative, les distributions de rendements des États-Unis, du Canada, du Royaume-Uni et de l’Allemagne étant significativement étirées vers la gauche. Le coefficient d’aplatissement (kurtosis) indique que toutes les distributions sont significativement plus pointues qu’une distribution normale.

1.1.2 Taux de change

Les volets B et C du tableau 1 présentent les principales caractéristiques des rendements des taux de change au comptant et des contrats à terme sur devises. La devise s’étant la plus appréciée relativement au dollar américain est le yen avec un rendement moyen de 4,37 % par année, alors que la lire italienne s’est la plus dépréciée (-3,39 % par année). Le yen et le deutsche mark se sont appréciés, alors que le dollar canadien, la livre sterling, le franc français et la lire italienne se sont plutôt dépréciés par rapport au dollar américain durant cette période. Le rendement du yen a été le plus volatil avec un écart type annualisé de 12,70 %, alors que l’écart type des rendements du dollar canadien représente moins de 40 % de la volatilité des autres devises (4,78 %). La plus importante différence entre le rendement sur les taux de change au comptant et sur les contrats à terme est observée pour la lire italienne avec une différence de 5 % par année. Alors que la volatilité de la prime à terme[7] est environ 10 fois moins élevée que la volatilité des taux au comptant, la volatilité des rendements des contrats à terme (volet C) est proche de celle des devises au comptant (volet B). En ce qui concerne les troisième et quatrième moments de la distribution, le yen présente une asymétrie positive et significative alors que le dollar canadien et la lire italienne présentent des asymétries significativement négatives. Toutes les devises à l’exception du deutsche mark ont des distributions statistiquement plus pointues que la normale.

1.2 Corrélations

Les corrélations entre les différents marchés boursiers présentées dans le volet A du tableau 2 sont relativement élevées pour la période de juillet 1976 à juin 2001, soit de l’ordre de 0,45. Les corrélations les plus faibles sont observées entre l’Italie et l’Amérique du Nord (0,28 avec les États-Unis et 0,33 avec le Canada), de même qu’entre le Japon et l’Allemagne (0,31) ainsi qu’entre le Japon et l’Amérique du Nord (0,34). Les marchés canadiens et américains sont les plus fortement corrélés avec un coefficient de corrélation de 0,73.

Les corrélations entre les rendements des taux de change au comptant (volet B, tableau 2) sont très proches de celles entre les rendements des contrats à terme sur devises (volet C, tableau 2) avec une moyenne de 0,50 dans les deux cas. Ces corrélations sont toutefois très différentes d’une devise à l’autre : la corrélation entre le yen et le dollar canadien est de 0,06, alors que celle entre le deutsche mark et le franc français est de 0,95. Comme les corrélations entre les devises de la zone européenne sont très élevées, il pourrait être opportun d’utiliser seulement une ou deux devises pour couvrir l’ensemble des investissements de cette région (couverture croisée). Quant aux corrélations entre le rendement des contrats à terme et des marchés boursiers (volet D, tableau 2), elles sont beaucoup plus faibles que les corrélations présentées dans les volets précédents avec une moyenne de -0,02. En valeur absolue, la moyenne de ces corrélations est de 0,10.

Tableau 1

Statistiques descriptives sur les rendements mensuels des marchés boursiers couverts en dollars américains, des devises et des contrats à terme sur devises pour la période de juillet 1976 à juin 2001

Tableau 1 (suite)

Le détail des calculs est présenté en annexe.

^1.

Rendement arithmétique.

^2.

Rendement des contrats à terme sur devises = (S₁ – F₀) / S₀ = –c

^*

Significatif au niveau de confiance de 95 %.

Tableau 2

Corrélations entre les rendements mensuels des marchés boursiers, des devises, des contrats à terme sur devises et entre les contrats à terme sur devise et les marchés boursiers pour la période de juillet 1976 à juin 2001

Tableau 2 (suite)

Note :* Significatif au niveau de confiance de 95%.

Malgré la globalisation croissante des marchés, Odier et Solnik (1993) sou­lignent que sur la période de 1970 à 1990, il n’existerait aucune tendance à la hausse significative des corrélations entre les marchés boursiers. Par ailleurs, Jorion (1989) soutient que l’effet de la couverture réduirait la volatilité des actifs, mais augmenterait la corrélation entre les actifs étrangers et les actifs américains, réduisant ainsi les bénéfices de la diversification. Dans cette optique, l’effet d’une couverture complète des investissements étrangers sur le risque global du portefeuille est incertain et cet aspect doit être considéré lors de l’adoption d’une politique de couverture du risque de change.

2. Comparaison des résultats des différentes approches

Nous présentons tout d’abord le cadre d’analyse, puis examinons les résultats empiriques des quatre approches définies selon les types retenus de 1) décision de répartition de l’actif d’un portefeuille d’actions internationales et de 2) décision d’exposition au risque de change.

2.1 Cadre d’analyse

Selon que les investisseurs institutionnels pensent ou non avoir une capacité à prévoir les rendements ou du moins la tendance à long terme des indices boursiers ou des devises, ils adopteront des politiques passives (pondération indicielle des différents marchés boursiers et politique de couverture du risque de change selon un pourcentage fixé d’avance) ou procéderont à des exercices d’optimisation. Les combinaisons de ces deux dimensions correspondent à quatre approches possibles que nous détaillons ci-dessous.

L’approche 1, dans laquelle la répartition des actions et la couverture du risque de change sont passives, utilise la moyenne de la capitalisation relative de chaque marché boursier (w^*_i) dans l’indice MSCI G-7. Les ratios de couverture passifs prennent les valeurs de 0 %, 50 % et 100 %. Dans l’approche 2, seule la pondération des marchés boursiers est déterminée par optimisation; la politique de couverture du risque de change étant appliquée de façon passive comme dans le cas précédent. Dans l’approche 3, la répartition de l’actif selon les marchés boursiers est établie de façon passive, comme dans le cas de l’approche 1; la couverture du risque de change est ensuite déterminée par optimisation[8]. Finalement, dans l’approche 4, les positions dans les différents marchés boursiers et la couverture du risque de change sont toutes deux déterminées par une optimisation. L’optimisation des positions dans les marchés boursiers et en devises peut se faire de façon séparée, séquentielle (optimisation partielle)[9] ou simultanée (optimisation conjointe). C’est l’optimisation conjointe qui sera utilisée ici puisqu’elle tient compte des corrélations existant entre les marchés boursiers et les devises pour déterminer simultanément les positions optimales dans les marchés boursiers et les devises.

Les paramètres de l’optimisation peuvent être définis de façon prospective ou rétrospective. Dans un objectif de gestion de portefeuille, l’estimation des paramètres relatifs au rendement, au risque et aux corrélations des différentes caté­gories d’actif repose sur des données prospectives. Ces prévisions servent alors d’intrants dans le modèle d’optimisation dit a priori. À l’inverse, à moins de poser l’hypothèse que le passé est garant de l’avenir, les données historiques ne peuvent être utilisées pour déterminer de façon précise les poids optimaux pour fins d’investissement. L’utilisation des données historiques dans les procédures d’optimisation dites a posteriori présentées dans cette étude vise plutôt à analyser l’augmentation relative de la performance obtenue selon différentes approches et selon l’ajout de différentes contraintes. Dans le cadre d’une optimisation a posteriori, étant donné que l’optimisation et la mesure de la performance portent sur la même période historique et que les intrants sont connus, l’optimisation conjointe conduira toujours à des résultats supérieurs ou égaux à ceux résultant d’une optimisation partielle (Jorion, 1994)[10]. Il en est ainsi puisque l’ensemble de l’infor­mation (le rendement, le risque et les interactions entre tous les actifs) est pris en compte dans la procédure d’optimisation conjointe.

2.2 Formalisation

À l’instar de Clarke et Kritzman (1996), nous utilisons les rendements couverts des indices boursiers pour les fins d’optimisation de la répartition du portefeuille d’actions internationales. Bien que Jorion (1994) utilise des rendements non couverts, il nous apparaît préférable de baser les décisions d’allocation d’actif sur les rendements couverts, puisque la prime ou l’escompte du contrat à terme (ou le différentiel de taux d’intérêt) qui sert d’ajustement au rendement local du marché sont connus au temps 0, contrairement au taux de change futur qui lui n’est pas connu initialement[11]. Le rendement partiellement couvert R_pc d’un porte­feuille d’actions réparties sur N + 1 pays sera alors égal au rendement totalement couvert du portefeuille, R_tc, plus le rendement lié à la découverture du portefeuille, R_déc[12] :

(1)

R_pc = R_tc + R_déc = w'R_tc – H'(f – e) = w'R_tc – H'c

avec w' = (w_d, w₁, ..., w_N); R'_tc = (R_d, R₁ + f₁, ..., R_N + f_N); H' = (H₁, ..., H_N)

et c'(f – e)' = (f₁ – e₁, ..., f_N – e_N)'

où

w_i: pondération du marché i (i = 1, …, N)  ,

w_d: pondération du marché domestique (États-Unis)  ,

R_d: rendement du marché domestique en dollars américains  ,

R_i: rendement du marché i en devise locale  ,

R_tci = R_i + f_i: rendement totalement couvert du marché i en dollars américains  ,

S_it: taux de change au comptant de la devise i en dollars américains au temps t = 0 ou 1  ,

F_i0: taux de change à terme de la devise i en dollars américains au temps 0  ,

prime ou escompte du contrat à terme sur la devise i  ,

rendement du taux de change au comptant de la devise i  ,

c_i = f_i – e_i : rendement de la couverture (R_tci – R_nci)

H_i: position à découvrir de la devise i (h_i = H_i – w_i , position couverte de la devise i).

La variance de ce portefeuille partiellement couvert s’exprime alors ainsi :

(2)

où ∑ représente une matrice de variances-covariances de dimension (2N + 1, 2N + 1) entre les rendements des indices de marchés boursiers (rendement domestique et rendements totalement couverts), entre les rendements de la couverture de chaque marché, ainsi qu’entre les rendements des indices de marchés boursiers et les rendements de la couverture.

L’optimisation de type moyenne-variance repose sur l’hypothèse de distribution normale des rendements ou sur l’hypothèse de fonction d’utilité quadratique. Le rejet de cette hypothèse de normalité des rendements peut donc biaiser les résultats des optimisations (Bekaert et al., 1998)[13]. Le critère d’optimisation d’un portefeuille peut être de minimiser le risque total (portefeuille de risque minimum), de maximiser l’utilité espérée ou encore de maximiser le ratio Sharpe (rendement excédentaire par unité de risque). À l’instar de Jorion (1994), c’est le ratio Sharpe qui sera maximisé dans les optimisations et qui servira par la même occasion de mesure de comparaison de la performance des différentes approches. En maximisant le ratio Sharpe plutôt que l’utilité espérée, nous n’avons pas à poser d’hypothèse en ce qui a trait au degré d’aversion au risque. Le portefeuille optimal maximisant le ratio Sharpe représente le portefeuille de tangence de la Capital Market Line (CML) sur la frontière efficiente. La fonction objective qui sera maximisée peut donc s’écrire comme suit :

(3)

2.3 Performance relative des quatre approches

Le tableau 3 présente le rendement et le risque historiques de même que la composition d’un portefeuille d’actions et de devises selon les quatre approches définies précédemment. Dans les cas où la répartition de l’actif selon les marchés boursiers fait l’objet d’une optimisation, deux contraintes simples sont retenues : soit que la totalité de l’actif soit investie et que les poids associés aux marchés boursiers soient à l’intérieur d’un intervalle de ± 25 % autour des pondérations indicielles moyennes (voir C_MB1 dans le tableau 4). Dans les cas où la décision d’exposition au risque de change fait l’objet d’une optimisation, seule la couverture est autorisée (voir C_D1 dans le tableau 4).

Les trois premières colonnes du tableau 3 présentent les résultats de l’approche 1, soit une stratégie de répartition passive d’un portefeuille d’actions selon trois politiques de couverture passive du risque de change (0 %, 50 % et 100 %). Le portefeuille d’actions est pondéré selon la moyenne de la capitalisation boursière relative des indices MSCI G-7 de juillet 1976 à juin 2001 (volet B). Au cours des 25 dernières années, les États-Unis ont représenté en moyenne plus de 50 % de l’indice MSCI G-7, suivis du Japon avec une pondération de 25 % et du Royaume-Uni (10,3 %). Le Canada, l’Allemagne, la France et l’Italie ont représenté ensemble moins de 15 % de la capitalisation du G-7. Le rendement et le risque (volet A) les plus élevés sont observés pour le portefeuille non couvert avec un rendement excédentaire annuel moyen de 7,56 % pour un écart type annualisé de 13,83 %. À l’inverse, le portefeuille couvert à 100 % a connu le rendement (7,21 %) et le risque (12,95 %) les plus faibles parmi les trois portefeuilles. En termes de performance globale, c’est toutefois le portefeuille couvert à 50 % qui a obtenu un ratio Sharpe légèrement supérieur (0,56) aux deux autres portefeuilles.

Les trois colonnes suivantes du tableau 3 présentent les résultats de l’approche 2, soit une optimisation (maximisation du ratio Sharpe) sur les rendements couverts des marchés boursiers combinée aux trois politiques de couverture passive. Compa­rativement à l’approche 1, cette approche conduit essentiellement à une diminution de la pondération du Japon et du Canada en faveur des autres pays (volet B). On observe une amélioration de la performance, telle que mesurée par le ratio Sharpe, quelle que soit la politique de couverture. C’est toujours le portefeuille couvert à 50 % qui connaît la meilleure performance avec un ratio Sharpe de 0,576 comparativement à 0,568 et 0,569 pour les portefeuilles non couvert et totalement couvert.

La colonne suivante présente les résultats de l’approche 3, soit une répartition passive pour les marchés boursiers (approche 1) combinée à un exercice d’optimisation pour la couverture du risque de change. Les investissements canadiens, japonais et allemands auraient alors dû être couverts à 100 %, alors qu’aucune couverture n’aurait dû être appliquée sur la livre sterling, le franc français et la lire italienne (volet B). Au total, 15,23 % du portefeuille n’aurait pas été couvert (positions ouvertes). Nous observons dans le volet A un ratio Sharpe de 0,574, supérieur à ceux de l’approche 1; les approches 2 et 3 ne sont toutefois pas réellement comparables[14]. Comparativement au portefeuille couvert à 50 % de l’approche 1, l’optimisation de la couverture du risque de change permet d’augmenter le rendement de 7 points centésimaux à 7,46 % et de réduire le risque de 19 points centésimaux à 13 %. Il en résulte un ratio Sharpe qui passe de 0,56 pour le portefeuille couvert à 50 % de l’approche 1 à 0,574 pour le portefeuille dont on a optimisé la couverture du risque de change.

Finalement, la dernière colonne du tableau 3 présente les résultats de l’approche 4, soit d’une optimisation conjointe sur les actions et les devises. Comme dans l’approche 3, la maximisation du ratio Sharpe conduit à une couverture complète des investissements canadiens, japonais et allemands, alors que l’absence de couverture aurait été préférable sur la livre sterling, le franc français et la lire italienne. C’est évidemment l’approche 4 avec l’optimisation conjointe des positions dans les marchés boursiers et en devises qui aurait conduit à la meilleure performance avec un ratio Sharpe maximisé de 0,59.

3. Importance des contraintes

Dans cette partie, nous analysons l’impact d’un relâchement des contraintes d’optimisation au niveau des actions et des devises sur la performance relative des portefeuilles déterminés par optimisation. Pour ce faire, nous ne retenons que l’approche 4, soit l’optimisation conjointe maximisant le ratio Sharpe.

3.1 Contraintes

Les contraintes d’optimisation font immanquablement l’objet de critiques, tant dans les milieux académique que professionnel. D’un côté, si l’on introduit peu de contraintes, les poids optimaux souffrent d’un manque de réalisme; d’un autre côté, le souci de refléter la réalité en imposant des contraintes trop restrictives limite l’intérêt de l’optimisation. Les contraintes choisies pour les optimisations résultent donc d’un compromis. Il nous apparaît important de tenir compte des contraintes auxquelles sont confrontés les gestionnaires tout en gardant l’essence de la procédure d’optimisation. Cela nous permet en outre d’analyser l’impact des contraintes et surtout d’un relâchement de celles-ci sur la répartition optimale du portefeuille et la performance qui en résulte.

En ce qui a trait aux contraintes relatives aux marchés boursiers, en plus de la contrainte minimale d’usage voulant que 100 % de l’actif soit investi (C_MB1a,C_MB2a), nous examinons deux options reliées à l’écart entre la position permise et le poids moyen du marché boursier considéré dans l’indice MSCI G-7 : soit des bornes de ± 25 % autour des pondérations indicielles, C_MB1b, comme dans la partie précédente, et des bornes de ± 50 %, C_MB2b. Ces contraintes sont décrites dans le volet A du tableau 4

Tableau 3

Performance historique et composition des portefeuilles selon différentes approches de répartition passive ou déterminée par optimisation pour la période de juillet 1976 à juin 2001

Tableau 3 (suite)

Tableau 4

Contraintes utilisées sur les positions en actions et contrats à terme sur devise pour les différentes optimisations

Le volet B du tableau 4 présente les contraintes relatives à l’exposition au risque de change (C_D). Quatre types de contraintes sont retenus. Selon la première (C_D1), que nous avons utilisée dans la partie précédente, seule une couverture du risque de change entre 0 % et le poids du marché boursier (w_i) est permise. Le second type de contraintes permet une couverture croisée (cross hedging) entre les devises de la zone européenne (C_D2b) alors que seule la couverture du risque de change est permise pour le Canada et le Japon (C_D2a). La couverture croisée implique une troisième contrainte limitant la somme de la couverture appliquée sur les quatre devises européennes à la somme de l’actif investi dans cette zone (C_D2c). Avec le troisième type de contraintes, nous permettons à la fois la couverture du risque de change et l’exposition aux devises par le biais de positions longues en contrats à terme sur devises (C_D3a), tout en nous assurant que l’exposition totale du portefeuille (positions ouvertes) ne soit pas supérieure au total investi à l’étranger (C_D3b). Finalement, l’alternative la moins contraignante permet à la fois la couverture croisée pour les devises européennes de même que l’exposition aux devises (C_D4).

3.2 Impact d’un relâchement des contraintes

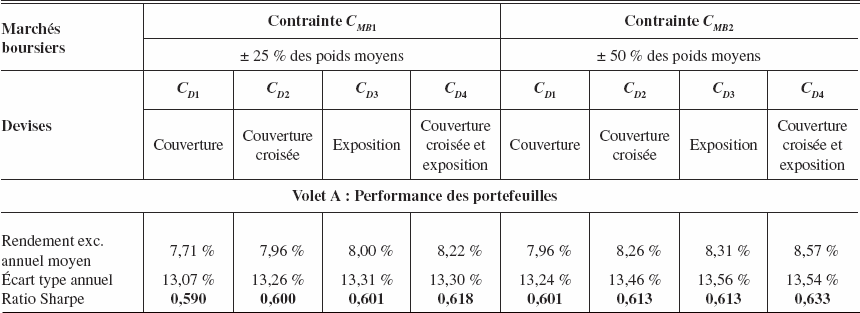
Dans le tableau 5, nous illustrons tour à tour l’impact d’un relâchement des contraintes sur les marchés boursiers (contraintes C_MB1 à C_MB2) et sur les devises (contraintes C_D1 à C_D4).

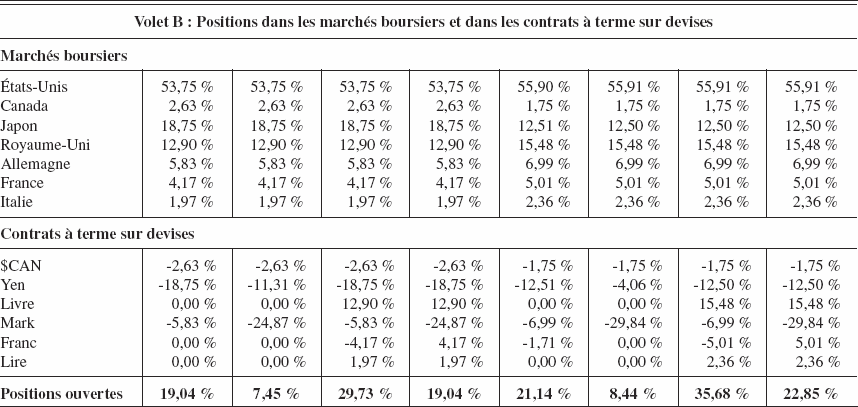
Plusieurs points méritent d’être soulignés quant à la performance historique et aux positions optimales dans les marchés boursiers et dans les contrats à terme sur devises. Dans un premier temps, tous les résultats des optimisations conjointes de ce tableau sont supérieurs à ceux des approches 1 à 3 présentés au tableau 3 puisqu’elles considèrent un plus vaste ensemble d’information[15]. Par ailleurs, pour un type de contrainte donné sur les devises (C_Dj, j = 1 à 4), le relâchement des contraintes sur les marchés boursiers (bornes passant de ± 25 % à ± 50 % autour de la pondération moyenne) résulte en une augmentation du rendement, mais aussi du risque des portefeuilles. Tous les ratios Sharpe sont améliorés. Par ailleurs, il est intéressant de noter que nous trouvons pratiquement la même répartition des marchés boursiers peu importe le type de contraintes sur les devises, et ce même si le portefeuille a été optimisé de façon conjointe. Cela signifie donc que les positions en devises n’ont pas eu d’impact sur les positions sur les marchés boursiers au cours de la période d’étude parce que les corrélations entre les marchés boursiers et les devises sont très faibles (tableau 2, volet D) ou que les contraintes sur les indices boursiers sont trop restrictives, ce qui est le cas ici puisque l’optimisation conduit à des poids correspondant à la borne minimale pour le Canada et le Japon et à la borne maximale pour les autres pays[16].

Pour un type de contrainte donné sur les marchés boursiers, le même phé­nomène est observé si l’on impose des contraintes moins restrictives sur les positions en contrats à terme sur devises. Le rendement et le risque augmentent lorsqu’on passe de la couverture standard (C_D1) à la couverture croisée pour les devises européennes (C_D2) et ensuite à l’exposition au risque de devise (C_D3). La seule exception concerne la contrainte la plus laxiste, permettant à la fois l’exposition au risque de devise et la couverture croisée (C_D4), où l’on observe une amé­lioration du rendement de même qu’une légère diminution du risque par rapport à la contrainte C_D3. De la contrainte la plus restrictive à la moins restrictive, le ratio Sharpe passe de 0,59 à 0,618 (de 0,601 à 0,633) pour les bornes de ± 25 % (± 50 %) autour du poids moyen de chaque marché boursier. Les portefeuilles permettant la couverture croisée (C_D2), l’exposition aux devises (C_D3) ou la combinaison des deux (C_D4) sont plus performants que les portefeuilles où seule la couverture standard est permise (C_D1). De même, la combinaison de la couverture croisée et des positions longues sur devises (C_D4) est plus optimale que les contraintes C_D2 et C_D3, la relation entre ces dernières étant toutefois plus ambiguë.

Au niveau de la répartition des positions en contrats à terme sur devises, les quatre types de contraintes conduisent à des pondérations assez différentes dans certains cas. En effet, alors que l’on couvrait la totalité des investissements japonais et allemands dans le cas C_D1, la couverture croisée (C_D2) permet de couvrir la totalité des investissements européens par le deutsche mark et de diminuer le ratio de couverture appliqué aux investissements japonais. Lorsque l’exposition aux devises est permise (C_D3), on couvre 100 % des investissements canadiens, japonais et allemands tout comme dans le cas C_D1. Toutefois, à la différence de la première contrainte, l’optimisation sous la contrainte C_D3 conduit à une couverture complète des positions sur le marché français et à une position longue en contrats à terme sur la livre sterling et la lire italienne. Finalement, avec la dernière contrainte (C_D4), tout comme dans la contrainte C_D3, on couvre 100 % des marchés canadiens et japonais et l’on prend une position longue sur la livre sterling et la lire italienne. La couverture complète des actifs européens est effectuée par le biais du deutsche mark comme dans C_D2. La seule différence a trait au franc où l’on prend une position longue plutôt qu’une position courte en contrats à terme. Ceci semble être causé par le besoin de garder une certaine exposition aux devises au niveau du portefeuille global (positions ouvertes) que l’on préserve en diminuant la couverture au Japon dans le cas C_D2 et en prenant une position longue sur le franc dans le cas C_D4. Finalement, l’exposition du portefeuille global (positions ouvertes) est légèrement plus élevée lorsque des bornes de ± 50 % autour des poids moyens sont utilisées.

Enfin, il est intéressant de noter que le passage d’un écart autorisé de ± 25 % à ± 50 % autour des poids moyens, ce qui est considérable dans le cas des États-Unis et du Japon, n’aurait augmenté le ratio Sharpe que de 0,013 en moyenne. À l’inverse, le fait de permettre les positions longues sur les devises ainsi que la couverture croisée (C_D4) aurait permis d’augmenter le ratio Sharpe de 0,03 par rapport à la couverture simple (C_D1).

Conclusion

Cet article examine la double décision de répartition de l’actif d’un portefeuille d’actions internationales et d’exposition au risque de change dans un cadre d’analyse considérant quatre approches possibles selon que l’allocation est déterminée de façon passive ou par optimisation. Il porte sur les rendements histo­riques des pays du G-7 sur la période de 1976 à juin 2001. À la différence de Jorion (1994) ou Clarke et Kritzman (1996), les optimisations correspondant aux stratégies de répartition de l’actif entre les marchés boursiers sont établies sous contraintes de ne pas s’écarter trop des poids relatifs de chacun des pays du G-7. De la même façon, les optimisations visant à déterminer les positions en contrats à terme sur devises sont effectuées sous différentes contraintes auxquelles sont généralement assujettis les gestionnaires de devises : couverture du risque de change seulement, couverture croisée ou possibilité d’augmenter l’exposition aux devises.

Selon l’approche 1, soit une répartition passive pour les actions et les devises, il apparaît sur la base du ratio Sharpe qu’un ratio de couverture du risque de change de 50 % aurait été supérieur à un ratio de non-couverture et de couverture à 100 %. Selon l’approche 2, où la répartition de l’actif selon les pays fait l’objet d’une optimisation alors qu’on applique une couverture du risque de change passive, un gestionnaire de portefeuille aurait pu améliorer sensiblement la performance d’un portefeuille d’actions internationales sur la base d’une optimisation a posteriori. Une couverture passive de 50 % aurait été encore une fois plus avantageuse en termes de ratio Sharpe qu’une couverture de 0 % ou de 100 %. Selon l’approche 3, où la répartition est déterminée de façon passive pour les actions et par optimisation pour la couverture du risque de change, il ressort que le ratio Sharpe est presque équivalent à celui de l’approche 2 dont le ratio de couverture est de 50 %. L’optimisation de la couverture du risque de change aurait donc pu avoir un impact aussi important en termes de mesure de performance qu’une optimisation de l’allocation des marchés boursiers autorisant des écarts de poids allant jusqu’à ± 25 % des poids moyens. Enfin, selon l’approche 4, soit l’optimisation conjointe des positions en actions et en devises, on observe une amélioration du ratio Sharpe.

Tableau 5

Performance historique des portefeuilles optimisés de façon conjointe et positions en actions et devises selon différentes contraintes pour la période de juillet 1976 à juin 2001

Tableau 5 (suite)

Dans le cas de l’optimisation conjointe, nous avons également évalué l’impact des contraintes imposées aux gestionnaires et du relâchement de celles-ci sur la performance d’un portefeuille d’actions internationales. Pour une même contrainte sur les devises, le relâchement de la contrainte sur l’écart des positions des marchés boursiers par rapport au poids de l’indice (de ± 25 % à ± 50 %) aurait eu un impact moins important que le fait de passer d’une situation de couverture simple du risque de change à une situation permettant la couverture croisée et l’augmentation de l’exposition à la devise.

Cet article illustre, en premier lieu, l’importance d’avoir une méthode systématique de la répartition de l’actif plutôt que de contourner cette décision capitale en se collant à une répartition passive. En second lieu, il illustre l’impact des contraintes plus ou moins sévères qui sont ni plus ni moins un mal nécessaire dans une procédure d’optimisation dont l’objectif est de fournir un outil d’aide à la décision. En aucun cas, nous ne prétendons qu’il est aussi aisé d’utiliser les procédures d’optimisation dans une approche a priori. Qui plus est, même si l’optimisation conjointe domine les autres approches dans une approche a posteriori, ce n’est pas nécessairement le cas lorsque les intrants du modèle sont des estimations sujettes à erreur. Les erreurs d’estimation pourraient en effet avoir des impacts non négligeables en raison de l’interdépendance entre les marchés boursiers et les devises. Il serait donc intéressant dans une étape ultérieure, de tester des modèles de prévisions dans une optique de détermination de la répartition d’actif par optimisation et d’analyser l’impact des erreurs de prévision si l’optimisation a lieu de façon conjointe, séquentielle ou séparée.

Notes

• [1] Ils affirment en outre que la contribution de la gestion active de l’allocation de l’actif et de la sélection de titres ne serait pas significativement différente de zéro.
• [2] Voir également Kerneis et Williams (2000), Baca, Garbe et Weiss (2000), Cavaglia, Brightman et Aked (2000).
• [3] Perold et Schulman (1988) affirment qu’un portefeuille couvert à 100 % contre le risque de change réduirait d’environ 20 % la volatilité par rapport à un portefeuille sans couverture.
• [4] Il précise que la couverture à 100 % réduirait substantiellement le risque de change, mais seulement à court terme (surtout sur un ou deux ans). Comme les investisseurs institutionnels ont généralement des horizons à long terme, il ne serait donc pas justifié d’utiliser une couverture complète qui réduit du même coup le rendement.
• [5] Un forward sur devise est un contrat à terme non standardisé entre deux parties concernant l’achat ou la vente d’un certain nombre de devises à un prix fixé aujourd’hui à une date ultérieure déterminée. L’échéance d’un mois est retenue puisqu’il s’agit des contrats les plus liquides.
• [6] Il s’agit de la moyenne arithmétique du prix acheteur et vendeur à la fermeture du marché de Londres.
• [7] Elle n’est toutefois pas reportée dans le tableau 1.
• [8] Bien que l’approche correspondant à la combinaison (politique passive de répartition de l’actif et optimisation de la politique de couverture du risque de change) ne soit pas courante dans la pratique, on l’utilise dans cette étude afin d’isoler l’impact de l’optimisation des positions en devises sur la performance globale du portefeuille.
• [9] L’optimisation partielle implique une première optimisation sur les marchés boursiers sans tenir compte des devises, suivie d’une seconde optimisation sur les devises, qui cette fois tient compte des positions sur les marchés boursiers trouvées préalablement et des corrélations entre les marchés boursiers et les devises.
• [10] Comme les optimisations a priori reposent sur des prévisions et que les paramètres ne sont donc pas connus avec certitude, l’optimisation conjointe ne donnera pas nécessairement des résultats supérieurs ou égaux aux autres approches. L’optimisation conjointe pourrait ne pas donner les meilleurs résultats si par exemple des erreurs de prévisions sur certains actifs se répercutaient sur d’autres actifs.
• [11] Le fait de retenir des rendement couverts ou non couverts n’a que peu d’impact dans une étude rétrospective (rendements calculés a posteriori). Toutefois, la mise en oeuvre de l’optimisation avec des rendements non couverts serait plus difficile dans le cadre d’une approche prospective (rendements estimés a priori). En effet, en utilisant le rendement non couvert du marché boursier, nous devrions à la fois faire une prévision du rendement du marché et de l’évolution des taux de change au comptant, pour l’exercice d’optimisation des positions sur les marchés boursiers.
• [12] Le détail du calcul des rendements couverts, non couverts et partiellement couverts est présenté en annexe.
• [13] Lorsque les distributions ne sont pas normales, la moyenne et l’écart type ne sont pas des statistiques suffisantes puisqu’elles ne tiennent pas compte des troisième et quatrième moments de la distribution. Cette réserve doit être gardée à l’esprit lors de l’interprétation des résultats.
• [14] La performance relative des approches 2 et 3 est plus difficile à déterminer a priori, mais il y a fort à parier que l’approche 2 domine l’approche 3 en utilisant des contraintes semblables sur les marchés boursiers et les devises dans la mesure où la décision relative aux marchés boursiers a sans doute plus de poids que celle relative aux devises.
• [15] Alors que l’optimisation conjointe tient compte du rendement, du risque et des corrélations entre tous les actifs du portefeuille pour déterminer les poids optimaux en une seule étape, les approches 1 à 3 ne tiennent pas compte d’une information aussi complète. Par exemple, l’approche 2 optimise les positions en actions sans tenir compte des devises qui peuvent néanmoins avoir un impact sur les actifs.
• [16] En laissant varier le poids de chaque marché entre 0 et 1, il ressort que la répartition du portefeuille d’actions est très différente selon que l’on considère les contraintes sur devises C_D1 à C_D4.