Fiabilité d’un dispositif d’évaluation de l’habileté à déterminer le résultat d’une chaîne d’opérations chez des élèves québécois du secondaire

Hébert, Marie-Hélène; Valois, Pierre; Scallon, Gérard; Frenette, Éric

doi:https://doi.org/10.7202/1034582ar

Introduction

L’arrivée du concept de compétence dans le champ de l’éducation a suscité une multitude de changements en cascade au sein de l’école québécoise, notamment sur le plan de l’évaluation. Cette interdépendance entre les mutations dans les programmes d’études et celles enregistrées dans le champ de l’évaluation scolaire ne date pas d’hier.

Au Québec, avant la venue du concept de compétence à l’école, les contenus à apprendre étaient découpés et hiérarchisés dans les programmes d’études sous forme d’objectifs pédagogiques. Dans le programme de mathématique pour la première année du secondaire (MEQ, 1993), discipline d’intérêt dans la présente étude, des énoncés précisaient en termes de comportements observables et mesurables ce que les élèves devaient être capables de faire à la fin d’une séquence d’apprentissage. La nomenclature du programme de 1993 a induit certaines pratiques d’évaluation dans les classes de mathématique. Pendant près de 15 ans, la tendance en évaluation certificative était aux examens qui s’harmonisent avec des contenus formulés selon une hiérarchie d’objectifs, souvent mesurés par des tâches simples (p. ex. : items à réponse choisie ou à réponse courte).

Alors que le programme de 1993 mettait en avant des contenus formulés d’après la séquence « verbe d’action − objet », la nouvelle mouture du programme de mathématique pour l’enseignement au premier cycle du secondaire (MELS, 2006a) favorise le développement des compétences. Si le concept de compétence n’occulte pas les contenus à apprendre, ceux-ci se voient néanmoins investis d’un tout autre rôle. Ils constituent en quelque sorte un bassin de ressources[1], nécessaires au développement des compétences. Jusqu’à tout récemment, la nouvelle tendance en évaluation dans les classes de mathématique québécoises allait de pair avec la singularité d’un programme par compétences : les tâches complexes nourrissaient les jugements portés sur les compétences et contribuaient à la notation, tandis que les tâches simples informaient sur la maîtrise des ressources, sans contribution aucune au bulletin de l’élève (MELS, 2006b, 2006c).

Dernièrement, le ministère de l’Éducation, du Loisir et du Sport[2] publiait la Progression des apprentissages en mathématique au secondaire (MELS, 2010a), un document complémentaire au programme de 2006 qui détaille et hiérarchise le bassin de ressources en question à la façon d’un programme par objectifs. Dans la foulée de cette publication, le MELS a annoncé son intention de revenir à une approche plus « traditionnelle » de l’évaluation. Si l’importance de vérifier la maîtrise des ressources dans un contexte formatif a toujours été d’actualité, il faut reconnaître que les mutations prescrites témoignent d’un retour en force du balancier ; depuis la rentrée scolaire de 2011, il y a lieu de faire contribuer l’évaluation de la maîtrise des ressources au bulletin de l’élève, au même titre que celle des compétences (MELS, 2010b, 2011). Une manière de faire qui reconduit d’emblée le questionnement sur la fiabilité des dispositifs d’évaluation de tâches simples. Si de telles études, héritées de la psychométrie classique, avaient été quelque peu délaissées par l’arrivée massive des tâches complexes dans les écoles (Hébert, Valois, & Frenette, 2008), elles risquent de ressortir de l’ombre, au Québec du moins.

Avec pour trame de fond l’école québécoise, la présente étude a pour objectif d’examiner, au moyen de la théorie de la généralisabilité[3], la fiabilité d’un dispositif d’évaluation employé pour évaluer chez des élèves la maîtrise d’une ressource mathématique à apprendre au premier cycle du secondaire : déterminer le résultat d’une chaîne d’opérations en respectant la priorité des opérations (MELS, 2010a). La fiabilité du dispositif s’en trouverait mieux assurée s’il était démontré que le rendement des élèves n’est pas tributaire des conditions particulières des tâches choisies pour apprécier ladite ressource, comme leur degré de réalisme et la complétude de leurs données.

En mathématique, il est traditionnel pour le MELS de distinguer les problèmes selon leur contexte et leurs données (MELS, 2006a ; MEQ, 1988). Dans son fascicule consacré à la résolution de problèmes publié en 1988, le MELS indique qu’un problème est à contexte :

réel, « s’il se produit effectivement dans la réalité » (p. 26),
réaliste, « s’il est susceptible de se produire réellement » (p. 26),
fantaisiste, « s’il est le fruit de l’imagination et qu’il est sans fondement dans la réalité » (p. 27), et
purement mathématique, « s’il fait exclusivement référence à des objets mathématiques : nombres, relations et opérations arithmétiques, figures géométriques, etc. » (p. 27).

Toujours dans le même document, dont les idées maîtresses ont été reprises dans le programme de mathématique de 2006, le MELS reconnaît que les problèmes sont à données :

complètes, s’ils « présentent, de façon explicite, toutes les informations nécessaires à leur résolution » (p. 30),
superflues, s’ils « présentent, de façon explicite, certaines informations qui ne sont pas nécessaires à leur résolution » (p. 30),
manquantes, s’ils « ne présentent pas, de façon explicite, toutes les informations nécessaires à leur résolution et tels que les élèves doivent trouver eux-mêmes les informations qui manquent » (p. 31), et
insuffisantes, s’ils « ne présentent pas, de façon explicite, toutes les informations nécessaires à leur résolution et tels que les élèves ne peuvent pas trouver eux-mêmes les informations qui manquent » (p. 31).

Seuls les contextes réaliste et purement mathématique, ainsi que les données complètes et superflues sont pris en considération dans la présente étude, parce qu’ils sont d’utilisation plus fréquente dans la classe de mathématique et plus faciles à manipuler en contexte expérimental que les autres types de contextes et de données. Il s’agit, dans ce contexte, de questionner la fiabilité d’un dispositif d’évaluation de l’habileté à déterminer le résultat d’une chaîne d’opérations dans lequel les tâches à faire résoudre par les élèves sont :

à contexte réaliste ou purement mathématique et
à données complètes ou superflues.

Dans l’optique d’établir si ladite habileté est tributaire ou non des tâches choisies pour l’apprécier, une sous-question s’ajoute à celle sur la fiabilité de la mesure : y a-t-il chez les élèves une différence de rendement entre les problèmes :

à contexte réaliste et purement mathématique et
à données complètes et superflues ?

Si l’examen de la fiabilité d’un tel dispositif d’évaluation apparaît inédit, des études déjà anciennes ont montré la plus grande difficulté :

des contextes purement mathématiques par rapport aux contextes réalistes (Caldwell & Goldin, 1979) et
des données superflues par rapport aux données complètes (Li, 1990).

Méthode

Avant d’en arriver à l’étude principale proprement dite, une démarche en quatre étapes (appelée ci-après « préexpérimentation ») a conduit à la production de tâches pour apprécier chez des élèves de première secondaire (12-13 ans) l’habileté à déterminer le résultat d’une chaîne d’opérations. Des problèmes « à contexte réaliste et à données complètes » ont d’abord été construits (étape 1), puis administrés à des élèves (étape 2). Parmi ces problèmes, certains ont été retenus sur la base d’un indice de difficulté calculé d’après le modèle de Rasch pour données dichotomiques (étape 3) pour ensuite être convertis en problèmes « à contexte purement mathématique » et « à données superflues » (étape 4). Ces étapes, et leur raison d’être, sont détaillées ci-après.

En plus d’assurer la clarté des problèmes auxquels seraient confrontés les élèves dans l’étude principale, la préexpérimentation visait ultimement à garantir qu’il soit possible d’associer aux facteurs liés à l’énoncé du problème manipulés (degré de réalisme et complétude des données), plutôt qu’à des effets parasites (p. ex. : ordre de grandeur des nombres), toute différence de rendement enregistrée chez les élèves entre les problèmes :

à contexte réaliste et purement mathématique et
à données complètes et superflues.

Préexpérimentation

Construction des problèmes

Quarante problèmes « à contexte réaliste et à données complètes », modulés sous la forme d’une somme de deux produits de nombres naturels (p. ex. : 83 × 9 + 79 × 8) ou de nombres décimaux (p. ex. : 2 × 2,39 + 4 × 2,19), ont été construits par des membres de l’équipe de recherche. Un exemple de problème « à contexte réaliste et à données complètes » construit pour les besoins de l’étude est reproduit en annexe. Au terme d’une démarche de validation conduite par un comité d’experts formé de deux professeurs de didactique des mathématiques, d’une enseignante de mathématique et de cinq étudiants des cycles supérieurs en éducation, 28 des 40 problèmes « à contexte réaliste et à données complètes », dont 14 avec nombres naturels et 14 avec nombres décimaux, ont été retenus en vue d’une passation auprès d’élèves de première secondaire.

Passation des problèmes

Puisqu’il s’est révélé irréalisable, faute de temps, de faire résoudre par un groupe d’élèves l’ensemble des 28 problèmes initialement prévus, un devis d’échantillonnage matriciel a été mis en place. Pour ce faire, deux problèmes avec nombres naturels et deux problèmes avec nombres décimaux, choisis au hasard parmi le lot, ont été retenus pour être passés à tous les élèves. Les 24 problèmes restants ont été répartis dans trois cahiers de tests, lesquels ont été distribués aléatoirement parmi 78 élèves (41 filles et 37 garçons) scolarisés dans trois classes de mathématique d’une même école (seuil de faible revenu = 2 ; indice du milieu socio-économique = 2)[4] dont les parents avaient consenti par écrit à ce qu’ils prennent part à la préexpérimentation. Au terme de la passation qui s’est échelonnée sur trois séances de 15 minutes sous la gouverne des enseignants responsables des classes de mathématique, 12 problèmes ont été administrés à chacun des élèves : quatre problèmes communs aux trois cahiers de tests et huit problèmes spécifiques.

Les réponses aux problèmes ont été corrigées de façon dichotomique par un seul correcteur d’après le barème de notation suivant : réponse juste (1 point) ou mauvaise réponse (0 point). Compte tenu de l’empan relativement réduit des patrons de réponse possibles à des tâches simples, il a été décidé de ne pas prendre en compte la démarche des élèves dans la correction des problèmes.

Choix des problèmes retenus au terme de la passation

Les tableaux 1 et 2 reprennent, pour les 28 problèmes administrés, l’indice de difficulté et l’erreur-type du modèle de Rasch pour données dichotomiques calculés à l’aide du logiciel Winsteps (version 3.32 ; Linacre, 2001) par domaine mathématique.

Tableau 1

Rendement des élèves aux problèmes avec nombres naturels administrés lors de la préexpérimentation : indice de difficulté selon le modèle de Rasch pour données dichotomiques et erreur-type

Tableau 2

Rendement des élèves aux problèmes avec nombres décimaux administrés lors de la préexpérimentation : indice de difficulté selon le modèle de Rasch pour données dichotomiques et erreur-type

Après examen de ces statistiques, il a été possible de créer quatre regroupements de quatre problèmes aux indices de difficulté les plus proches possible (deux regroupements chez les naturels et deux chez les décimaux). Les problèmes 5, 7, 10 et 13 ont constitué le premier regroupement chez les naturels, tandis que les problèmes 2, 3, 6 et 11 ont fait partie du second. Du côté des décimaux, les regroupements ont été formés de la façon suivante : regroupement 1 pour les problèmes 18, 19, 21 et 26 et regroupement 2 pour les problèmes 17, 20, 24 et 25.

Conversion des problèmes retenus pour l’étude principale

Pour atteindre l’objectif de l’étude, il restait à ce stade à construire des problèmes à contexte purement mathématique et à données superflues. La démarche qui a conduit à la rédaction de ces problèmes est décrite ci-après pour chacun des regroupements de problèmes formés chez les naturels (2 regroupements) et chez les décimaux (2 regroupements) :

Un premier problème « à contexte réaliste et à données complètes » a été sélectionné aléatoirement parmi les quatre problèmes du regroupement. Il porte ci-après le nom de problème « pivot » et sert de point de référence.
Un deuxième problème « à contexte réaliste et à données complètes » a été choisi au hasard parmi les trois problèmes restants du regroupement pour ensuite être modifié par la transformation de son contexte d’origine en un contexte purement mathématique. Puisque les premier et deuxième problèmes étaient de niveau de difficulté voisin avant l’ajout d’un contexte purement mathématique au second, une éventuelle différence de rendement entre le problème « pivot » et le problème « à contexte purement mathématique » nouvellement créé pourra être attribuable, en grande partie du moins, au degré de réalisme du problème. Un exemple de la transformation qui s’est opérée sur le deuxième problème choisi au hasard est montré en annexe.
Le troisième problème « à contexte réaliste et à données complètes » pigé a été modifié par l’ajout de données superflues à son énoncé. Puisque les premier et troisième problèmes étaient de niveau de difficulté voisin avant l’ajout de données superflues au troisième, une éventuelle différence de rendement entre le problème « pivot » et le problème « à données superflues » nouvellement créé pourra être attribuable, en grande partie du moins, à la complétude des données du problème. Un exemple de la transformation qui s’est opérée sur le troisième problème pigé est montré en annexe.
Le quatrième et dernier problème du regroupement a été laissé de côté[5].

La répartition des problèmes retenus en prévision de l’étude principale par structure de problèmes est reproduite au tableau 3.

Étude principale

Échantillon

Les 12 problèmes ont été administrés à 82 élèves de première secondaire (44 filles et 38 garçons) n’ayant pas pris part à la préexpérimentation, issus d’une même école (seuil de faible revenu = 2 ; indice du milieu socio-économique = 2) et scolarisés dans trois classes de mathématique distinctes. Un formulaire de consentement à l’étude a été signé par l’un des parents de chacun des élèves. Parce qu’il s’agissait de faire résoudre des problèmes dont les types de contextes et de données sont prévus dans le programme de mathématique (MELS, 2006a), les élèves ont été considérés comme familiers avec des problèmes d’une telle nature.

Collecte des données

Le mandat d’administrer les problèmes aux élèves a été confié aux enseignants responsables des classes de mathématique. Ces enseignants volontaires, au nombre de trois, ont été rencontrés au préalable afin d’uniformiser la marche à suivre. La passation des problèmes s’est déroulée sur quatre séances d’une quinzaine de minutes chacune. Les élèves ont dû résoudre l’ensemble des problèmes de façon individuelle et sans l’aide d’une calculatrice. Ils étaient libres de laisser, ou non, des traces de leur démarche. Les cahiers de tests remplis ont été récupérés auprès des enseignants au terme de la quatrième séance de passation.

Les réponses aux problèmes ont été corrigées de façon dichotomique par un seul correcteur : réponse juste (1 point) ou mauvaise réponse (0 point). À l’instar de la préexpérimentation, la démarche des élèves n’a pas été retenue comme critère d’évaluation pour apprécier la performance des élèves.

Plan d’analyse

Afin d’évaluer la fiabilité du dispositif employé pour évaluer l’habileté des élèves à déterminer le résultat d’une chaîne d’opérations lorsque sont manipulés des facteurs liés à l’énoncé du problème, les données ont été analysées en appliquant la théorie de la généralisabilité au moyen du logiciel EduG (version 5.0 ; Cardinet, Johnson, & Pini, 2010). Ce choix se justifie par la singularité du modèle statistique, qui permet notamment de déterminer si des observations sont « indépendantes » ou non du dispositif d’évaluation qui a permis de les recueillir (Pini & Hexel, 1998). Comme le requiert toute étude de généralisabilité, les données collectées ont été structurées suivant les plans d’observation, d’estimation et de mesure décrits ci-après.

Plan d’observation. Dans le contexte de l’étude, quatre facettes peuvent être distinguées : les Élèves (E), les Structures de problèmes (S), les Domaines mathématiques dans lesquels s’inscrivent les problèmes (D) et les Problèmes (P :DS). La facette Élèves comporte 66 niveaux (66 élèves ayant pris part aux quatre séances de passation[6]), la facette Structures de problèmes, trois niveaux (problèmes « pivot », « à contexte purement mathématique » et « à données superflues »), la facette Domaines mathématiques, deux niveaux (nombres naturels et nombres décimaux), et la facette Problèmes, deux niveaux (deux problèmes par croisement Structures de problèmes × Domaines mathématiques). Un résumé du plan d’observation du dispositif à l’étude est présenté au tableau 4.

Tableau 4

**Dispositif d’évaluation : plan d’observation**

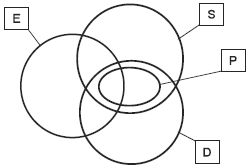
Puisque chaque élève, en résolvant chacun des problèmes, a rencontré chacune des structures de problèmes et chacun des domaines mathématiques, la facette Élèves a été « croisée » avec les facettes Problèmes (E × P :DS), Structures de problèmes (E × S) et Domaines mathématiques (E × D). Étant donné que chacune des structures de problèmes a fait intervenir chacun des domaines mathématiques, la facette Structures de problèmes a elle aussi été considérée comme « croisée » avec la facette Domaines mathématiques (S × D). Enfin, puisque chaque problème s’est inscrit à la fois dans une structure de problèmes particulière et dans un domaine mathématique particulier, la facette Problèmes a été « nichée » dans l’interaction entre les facettes Structures de problèmes et Domaines mathématiques. Les données pertinentes à l’étude ont été traitées selon le plan d’observation E(P :DS) illustré à la figure 1.

Figure 1

**Illustration du plan d’observation du dispositif d’évaluation**

Plan d’estimation. En présumant que les 66 élèves ont été choisis parmi des milliers d’élèves et que les 12 problèmes ont été puisés à même des milliers de problèmes, les facettes E et P :DS ont été qualifiées d’« aléatoires infinies ». Puisqu’il existe d’autres structures de problèmes[7] et d’autres domaines mathématiques[8] susceptibles d’être enseignés aux élèves de première secondaire, il a été décidé de considérer les facettes S et D comme « aléatoires finies ». Le tableau 5 rapporte ces informations.

Plan de mesure. Dans l’optique de différencier les élèves quant à leur habileté à déterminer le résultat d’une chaîne d’opérations au moyen des structures de problèmes (S), des domaines mathématiques (D) et des problèmes (P :DS), le plan de mesure E/DPS a été retenu.

Tableau 5

**Dispositif d’évaluation : plan d’estimation**

Résultats

Statistiques descriptives

Les tableaux 6 et 7 indiquent le rendement des élèves aux problèmes administrés lors de l’étude principale par structure de problèmes et par domaine mathématique. Il est à remarquer que les taux de réussite aux problèmes sont particulièrement faibles. Un seul problème, parmi les 12 administrés, avoisine les 80 % de réussite.

Tableau 6

**Rendement des élèves aux problèmes avec nombres naturels administrés lors de l’étude principale par structure de problèmes**

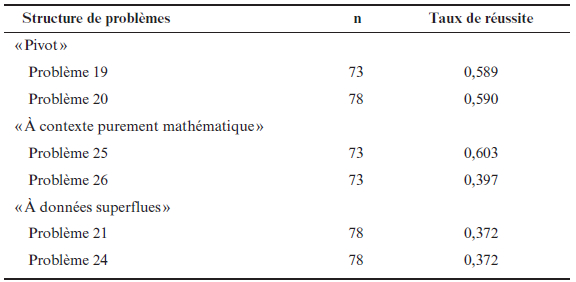
Tableau 7

**Rendement des élèves aux problèmes avec nombres décimaux administrés lors de l’étude principale par structure de problèmes**

Des analyses (test des signes) conduites avec le logiciel SPSS (version 18) montrent que les problèmes à contexte réaliste ne sont pas plus difficiles à résoudre pour les élèves que les problèmes à contexte purement mathématique (nombres naturels : z (69) = 0,000 ; p = 1,000 ; nombres décimaux : z (67) = –1,739 ; p = 0,082). À l’inverse, il apparaît que les problèmes à données superflues sont plus difficiles à résoudre pour les élèves que les problèmes à données complètes (nombres naturels : z (71) = –6,742 ; p = 0,000 ; nombres décimaux : z (71) = –3,714 ; p = 0,000)[9].

Étude de généralisabilité

Le tableau 8 synthétise les résultats de l’étude de la généralisabilité du dispositif d’évaluation au moyen du logiciel EduG.

Les coefficients de généralisabilité relatif (0,57) et absolu (0,48) n’atteignent pas le seuil traditionnellement requis (0,80 ; Bain & Pini, 1996)[10]. Un examen des sources de variation indique que c’est l’interaction Élèves × Problèmes (EP :DS) qui concourt le plus à l’erreur de mesure dans l’appréciation de l’habileté des élèves à déterminer le résultat d’une chaîne d’opérations. En comparant son importance relative à celle des autres sources de variation, les résultats du tableau 8 montrent que sa valeur (0,01571) représente 79 % de la variance d’erreur relative et 54 % de la variance d’erreur absolue. La source d’erreur la plus importante après l’interaction EP :DS est l’effet principal Structures de problèmes (S : 26 % de la variance d’erreur absolue), suivi de l’interaction Élèves × Structures de problèmes (ES : 15 % de la variance d’erreur absolue). En poursuivant l’étude de généralisabilité dans le but d’améliorer le dispositif d’évaluation, on estime que l’administration additionnelle de 66 problèmes[11] aux élèves aurait été nécessaire pour l’obtention d’une valeur acceptable du coefficient relatif (dans le cas du coefficient absolu, la passation d’une centaine de problèmes supplémentaires n’aurait même pas suffi). À l’opposé, une analyse de facettes a montré que l’élimination d’un domaine mathématique particulier ou d’une structure de problèmes particulière n’aurait pas conduit à de meilleurs coefficients de généralisabilité pour le dispositif d’évaluation.

Tableau 8

**Étude de généralisabilité du plan de mesure E/DPS**

Discussion et conclusion

La présente étude a examiné la fiabilité d’un dispositif d’évaluation employé pour évaluer chez des élèves l’habileté à déterminer le résultat d’une chaîne d’opérations en respectant la priorité des opérations lorsque sont manipulés deux facteurs liés à l’énoncé du problème : son degré de réalisme (réaliste ou purement mathématique) et la complétude de ses données (complètes ou superflues).

À la lumière des résultats obtenus, il n’y a pas lieu de recommander le dispositif d’évaluation dans son état actuel pour évaluer avec une fiabilité certaine l’habileté des élèves à déterminer le résultat d’une chaîne d’opérations. Les résultats observés aux 12 problèmes sont davantage le reflet de fluctuations aléatoires, introduites par le dispositif d’évaluation, que du véritable potentiel des élèves à déterminer le résultat d’une chaîne d’opérations.

La mise en évidence d’une interaction statistique Élèves × Problèmes, commune à plusieurs dispositifs d’évaluation (Lane, Liu, Ankenmann, & Stone, 1996; Randhawa & Hunter, 2001; Shavelson, Baxter, & Gao, 1993), soulève une inquiétude au sujet de la méthodologie de l’évaluation : le rendement des élèves varierait d’un problème à l’autre, et ce, indépendamment de leur habileté à déterminer le résultat d’une chaîne d’opérations et du degré de difficulté des problèmes à résoudre. Dans ce contexte, il devient alors souhaitable, comme l’a suggéré l’étude d’optimisation, de recourir à un nombre plus élevé de problèmes que n’en contient le dispositif d’évaluation pour évaluer l’habileté des élèves à déterminer le résultat d’une chaîne d’opérations. C’est d’ailleurs ce que dicte la théorie de l’échantillonnage : plus l’échantillon de problèmes à faire résoudre par les élèves est grand, plus la somme des erreurs aléatoires de mesure qui affectent leur rendement devrait tendre vers zéro.

En somme, la question qui se pose est la suivante : l’habileté des élèves à déterminer le résultat d’une chaîne d’opérations en respectant la priorité des opérations est-elle indépendante des conditions particulières des problèmes ? Les résultats de l’étude invitent à la prudence : il s’agirait plutôt d’une habileté limitée à des contextes particuliers, comme l’a montré l’étude de généralisabilité par la mise en évidence d’une interaction Élèves × Problèmes et d’un effet principal Structures de problèmes. Le rendement des élèves dépendant des problèmes dans lesquels ils sont placés, il devient inévitable de considérer les tâches retenues pour évaluer l’habileté des élèves à déterminer le résultat d’une chaîne d’opérations. Le phénomène, documenté en éducation notamment (p. ex. : Linn & Burton, 1994), est connu sous le nom de spécificité de la tâche (task specificity).

Les conclusions de l’étude conduisent à formuler des recommandations à l’intention des enseignantes et des enseignants qui oeuvrent dans le domaine de la mathématique. D’abord, étant donné que les problèmes à données superflues ont été plus difficiles à résoudre pour les élèves que les problèmes à données complètes, il y a lieu d’interpréter ce résultat comme un point valable pour encourager l’entraînement des élèves dans la résolution de problèmes d’une telle nature. Ensuite, en raison du degré de fiabilité limité du dispositif d’évaluation, et ce, malgré un contrôle très serré dans la rédaction des problèmes à faire résoudre par les élèves, il convient de suggérer que le personnel enseignant ait recours au plus grand nombre de problèmes qu’il soit possible d’administrer dans le contexte de leur classe pour évaluer l’habileté des élèves à déterminer le résultat d’une chaîne d’opérations en respectant la priorité des opérations.

Les limites engendrées par nos choix méthodologiques se situent à deux niveaux. Dans le but d’attribuer d’éventuelles différences au niveau du rendement des élèves aux facteurs liés à l’énoncé du problème manipulés, il a été décidé de former quatre regroupements de problèmes de niveau de difficulté voisin pour ensuite créer trois structures de problèmes qui ont servi à l’étude principale. Une limite de l’étude tient au fait que les indices de difficulté qui ont servi à la composition des regroupements n’étaient pas identiques chez les problèmes d’un même regroupement. Par conséquent, il est possible d’envisager que les variations, ou absence de variation, enregistrées sur le plan du rendement des élèves aux problèmes (a) à contexte réaliste et purement mathématique et (b) à données complètes et superflues ne soient pas à cent pour cent expliquées par les facteurs manipulés liés à l’énoncé du problème.

Une deuxième limite, liée à celle qui vient d’être énoncée, concerne le faible échantillon d’élèves retenu en préexpérimentation. Bien que Linacre (1994) ait avancé que le modèle de Rasch puisse offrir des estimés assez stables lorsqu’employé avec des échantillons de l’ordre de 50 participants, il y a lieu de croire qu’un nombre supérieur d’élèves aurait mené à des estimations plus précises des indices de difficulté (c.-à-d. à des erreurs-types plus faibles).

Malgré ses limites, l’étude ouvre la voie à un champ de recherche dans lequel d’autres chercheurs pourraient s’investir pour assurer la fiabilité des dispositifs d’évaluation de tâches simples, et même de tâches complexes, en mathématique. Parmi les avenues de recherche à explorer, il pourrait s’agir de poursuivre des efforts empiriques afin de déterminer l’ensemble des conditions nécessaires pour l’obtention de dispositifs d’évaluation fiables, dont le nombre minimal de tâches à y inclure. Par ailleurs, il serait souhaitable de reprendre l’étude en exploitant d’autres facteurs liés à l’énoncé du problème laissés en plan. Par exemple, les contextes réels, ainsi que les données manquantes et insuffisantes.

Au final, malgré la simplicité apparente des tâches et le respect de prescriptions ministérielles, l’étude a montré la difficulté d’évaluer avec un bon niveau de fiabilité une ressource mathématique à apprendre au premier cycle du secondaire. Que dire alors de l’évaluation des compétences par les tâches complexes ?

Fiabilité d’un dispositif d’évaluation de l’habileté à déterminer le résultat d’une chaîne d’opérations chez des élèves québécois du secondaire

Note des auteurs

Résumé

Abstract

Resumo

Introduction