Corps de l’article

1. Introduction: la résolution de problèmes écrits et la pensée algébrique

Les difficultés des élèves en résolution de problèmes écrits sont bien documentées par les chercheurs (p. ex. Lesh et Zawojewski, 2007). Notre équipe s’intéresse à cette problématique depuis 2008. Dans notre travail sur la résolution de problèmes écrits ayant des structures additives simples, nous nous inspirons des travaux de Vassili Davydov, un psychologue russe qui préconise le développement du raisonnement abstrait dès le début du parcours scolaire. Ses idées nous ont permis de développer et d’implanter, dans le contexte du système scolaire québécois, une séquence d’enseignement ayant pour but d’amener les élèves du premier cycle du primaire (âgés de 6 à 8 ans) à raisonner sur les problèmes écrits, traditionnellement appelés arithmétiques, en termes de relations entre les quantités et ainsi améliorer leur capacité de résoudre des problèmes de structures additives (Gervais et al., 2013; Polotskaia, 2015; Savard et Polotskaia 2017). Les chercheurs (p. ex. Squalli, 2003; Schmidt et Bednarz, 2002) associent le terme «raisonnement algébrique», entre autres, avec le raisonnement impliquant l’analyse de structures et de relations quantitatives ainsi que l’utilisation de l’idée d’égalité et de balance comme relation d’équivalence dans une déduction logique. À l’instar de chercheurs de l’école de Davydov, nous considérons la pensée qui s’appuie sur les relations quantitatives (la relation additive entre autres) comme précurseur du raisonnement algébrique et nous allons utiliser le terme «pensée relationnelle» pour l’évoquer. Dans notre article, nous allons utiliser l’expression «pensée algébrique» plutôt que «raisonnement algébrique» pour souligner le caractère préliminaire et non formel de ce que nous analysons. Nous allons aussi expliciter le lien entre la pensée relationnelle et la pensée algébrique.

Dans plusieurs expérimentations menées en Russie (Davydov, 1982; Mikulina, 1991), des lettres ont été utilisées très tôt dans l'apprentissage (à l’âge de 7 à 9 ans) pour exprimer les relations entre des quantités dans le contexte de résolution de problèmes écrits et ainsi promouvoir la pensée abstraite, potentiellement algébrique.

Le développement de la pensée algébrique ainsi que la transition arithmétique-algèbre, souvent difficile pour les élèves, préoccupent les chercheurs depuis des années. La pensée algébrique inclut, entre autres, savoir reconnaître et opérer sur les relations quantitatives variées (Kieran, 2014; Squalli, 2007; Blanton et al., 2015; Cai et al., 2005). Selon les écrits scientifiques, plusieurs éléments de la pensée algébrique sont accessibles aux élèves très tôt dans leur apprentissage des mathématiques à l’école. Par exemple, des recherches mettent en évidence les capacités des jeunes enfants à généraliser des motifs (patterns) à partir de suites numériques et géométriques (Lee et Freiman, 2006; Boily et al., 2015) et de travailler avec des équations et des lettres (Blanton et al., 2015; Mikulina, 1991). Aussi, certains chercheurs (Schmidt et Bednarz, 2002) ont utilisé le contexte de résolution de problèmes écrits pour étudier le développement de la pensée algébrique. Bref, nous partons de l’hypothèse que l’analyse des relations quantitatives et l’utilisation des lettres dans le contexte de résolution de problèmes écrits peuvent potentiellement favoriser le développement de la pensée algébrique chez les jeunes élèves.

Comme objet de recherche, nous nous intéressons principalement aux éléments de la pensée algébrique tels que savoir reconnaître et opérer sur les relations quantitatives variées. Plus précisément, notre expérimentation a visé la relation additive, définie par Davydov (1982) comme étant «the law of composition by which the relation between two elements determines a unique third element as a function» (p.229). Cette relation, parfois appelée «partie-partie-tout», est présente dans tous les problèmes arithmétiques qui peuvent être résolus par une addition ou par une soustraction.

Nos publications antérieures portaient sur divers aspects de l’expérimentation menée entre 2011 et 2014 qui avait comme but de soutenir l’apprentissage de résolution des problèmes ayant des structures additives pour les élèves du premier cycle du primaire au Québec. Entre autres, nous avons analysé et décrit les stratégies de résolution de problèmes utilisées par les élèves avant et après le traitement expérimental (Polotskaia, 2015; Polotskaia et al., 2016), ainsi que l’appropriation graduelle des stratégies didactiques nouvelles par les enseignantes lors de l’implantation des activités expérimentales (Savard et Polotskaia, 2014). Nous avons aussi analysé certaines activités expérimentales du point de vue de leur impact possible sur les apprentissages des élèves (Freiman et al., 2017; Savard et Polotskaia, 2017). Dans cet article, notre analyse se concentre spécifiquement sur l’émergence de la pensée algébrique dans le contexte expérimental, notamment le traitement des relations, la déduction logique et l’utilisation par les élèves du langage mathématique formel. Un modèle des trois mondes mathématiques qui s’appuie sur les idées de Van Hiele (1999) et de Tall (2013) nous sert de cadre conceptuel.

2. Du paradigme relationnel vers les trois mondes mathématiques

Une exploration théorique de la résolution des problèmes écrits d’addition et de soustraction à l’école primaire nous amène à y distinguer deux paradigmes: celui que nous appelons opérationnel et un autre dit relationnel (Polotskaia, 2017). Dans le «paradigme opérationnel», les problèmes écrits sont vus comme un outil d’apprentissage des opérations arithmétiques. Les curriculums (traditionnels) développés dans ce paradigme proposent d’abord l’apprentissage du dénombrement, du calcul avec des nombres naturels relativement petits, et la résolution de problèmes simples pour mettre les opérations en application. Ceci est le cas, par exemple, du programme de mathématiques au Nouveau-Brunswick francophone. En reconnaissant l’arithmétique (sens du nombre et opérations) comme l’un des cinq domaines des mathématiques, le programme place la résolution de problèmes écrits ayant une structure additive simple comme résultat d’apprentissage appartenant explicitement au domaine de l’arithmétique. En même temps, l’algèbre (régularités et relations), également considérée comme domaine, héberge une étude de l’égalité comme résultat d’apprentissage spécifique dès la 2e année, ce qui comprend, entre autres, l’utilisation de symboles mathématiques (lettres) ainsi que la tâche de trouver la valeur d’une inconnue dans une équation simple. Puisqu’on ne mentionne pas le contexte de résolution de problèmes dans ces visées, le type de liens que pourra faire l’élève entre les deux domaines demeure nébuleux. Ce que nous apprennent les recherches: l’enseignement basé sur ce paradigme opérationnel (qui sépare artificiellement les relations quantitatives du contexte de la résolution de problèmes) est propice pour le développement du raisonnement basé sur la connaissance des nombres (naturels) et les opérations, autrement dit le raisonnement arithmétique.

Au contraire, le paradigme relationnel considère les relations quantitatives comme le savoir préalable par rapport au calcul et à l’apprentissage des opérations. Selon Davydov (1998), la recherche des relations fondamentales dans chaque situation donnée est à la base de l’apprentissage: «This action [learning] is aimed at the search for an initial relation of the situation's object conditions that forms the general basis from which the whole multitude of particular problems can be solved later» (p. 7). Ainsi, le but de la résolution des problèmes écrits, dans le paradigme relationnel, est de mieux saisir le sens des relations décrites et d’opérer sur celles-ci à partir d’une modélisation appropriée (exprimée sous forme de schémas ou d’équations avec des lettres). Contrairement au paradigme opérationnel, l’analyse relationnelle et la modélisation par schéma ou équation rend explicites les liens entre la situation (problème écrit) et sa structure mathématique (voir algébrique). Autrement dit, le paradigme relationnel serait plus approprié pour soutenir le développement de la pensée algébrique (dans la partie de l’opérationnalisation des relations).

Pour clarifier la distinction entre les deux paradigmes, voici un exemple de problème:

Il y avait 21 tulipes dans le vase. Mela a pris des tulipes. Il y a maintenant 13 tulipes. Combien de tulipes Mela a-t-elle prises dans le vase?

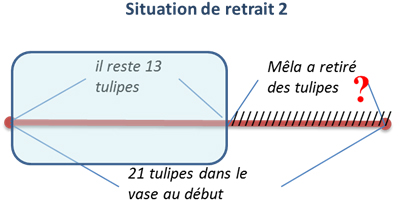
Pour résoudre ce problème, l’élève peut placer 21 jetons et les enlever un par un jusqu’à ce qu’il en reste 13. L’élève peut ensuite compter les jetons enlevés pour répondre à la question du problème. Selon le paradigme opérationnel, cette solution démontre une compréhension du sens de l’opération de soustraction, car l’élève interprète correctement la situation comme un acte de soustraction. Du point de vue du paradigme relationnel (Davydov, 1982), cette approche ne mène pas nécessairement l’élève vers une compréhension de la relation additive, qui peut être décrite par le raisonnement suivant: «Les tulipes dans le vase au début de la situation constituent deux parties: les tulipes prises par Mela et les tulipes qui restent». Ainsi, en restant dans le cadre du paradigme opérationnel, l’élève peut ne pas remarquer cette relation, mais simplement mimer l’histoire et ainsi visualiser la quantité recherchée (Polotskaia, 2015). Par contre, une modélisation effectuée dans le cadre du paradigme relationnel pourrait décrire cette relation à l’aide d’une équation 21–x=13 ou 21-?=13. Pour aider les élèves dans cette démarche de modélisation des relations, dans le cadre de notre projet, nous avons utilisé les schémas que nous avons nommés Range-Tout[1] (Figure 1) pour représenter les relations quantitatives de façon plus visuelle.

Figure 1

Le problème des tulipes représenté par un schéma Range-Tout

Le problème des tulipes représenté par un schéma Range-Tout

-> Voir la liste des figures

Chaque représentation, soit par l’équation ou par le schéma, explicite la relation en permettant un regard nouveau et plus abstrait sur le problème pouvant contribuer au développement des stratégies nouvelles de résolution. L’équation, une méthode algébrique typiquement introduite au secondaire, décrit et permet de manipuler avec l’équivalence. Le schéma représente visuellement les relations entre les grandeurs. Ainsi, l’utilisation de schémas ouvre la possibilité de manipuler à la fois le tout et ses parties. Pour identifier ou voir la partie inconnue du schéma ci-haut (Figure 1), nous considérons tout le segment représentant les tulipes du début et nous cachons la partie connue (les tulipes qui restent, Figure 2).

Figure 2

Manipulation sur le schéma: cacher la partie connue pour voir la partie inconnue

Manipulation sur le schéma: cacher la partie connue pour voir la partie inconnue

-> Voir la liste des figures

Les deux formes de représentation, les équations (forme symbolique) et les schémas (forme imagée), ouvrent la possibilité d’opérer sur des relations de façon algébrique. Dans le contexte du programme de mathématiques actuel au Québec, nous avons tenu compte du fait que les enfants ont déjà développé une culture de résolution de problèmes par l’arithmétique (travaillant dans le paradigme opérationnel). Le format imagé nous a paru plus plausible pour diriger la pensée mathématique des élèves vers l’analyse des relations (pensée algébrique).

Nous voulions ainsi que les élèves soient capables d’analyser le problème en portant leur attention sur la relation additive qu’il comporte et qu’ils deviennent plus efficaces dans leur résolution. En même temps, le raisonnement relationnel que nous souhaitions former chez l’élève peut potentiellement contribuer au développement du raisonnement algébrique plus tard, car reconnaître et opérer sur les relations quantitatives fait partie du raisonnement algébrique (Kieran, 2014; Squalli, 2007; Blanton et al., 2015; Cai et al., 2005). Afin d’articuler plus clairement la nature du processus de passage des objets physiques vers les relations puis ultérieurement vers une pensée algébrique qui a été provoquée chez les élèves dans notre expérimentation, nous nous inspirons de la théorie des trois mondes mathématiques de Tall (2013) que nous présentons dans la section suivante.

3. Les trois mondes mathématiques de Tall et la pensée algébrique

La théorie des trois mondes mathématiques proposée par Tall (2013) en continuité avec la théorie d’abstraction mathématique de Van Hiele (1999) nous offre un cadre théorique intéressant pour analyser le passage des manipulations physiques avec les objets vers les manipulations algébriques avec des lettres en passant par la manipulation sur les relations. Van Hiele (1999) a utilisé le contexte de la géométrie pour décrire comment la pensée mathématique se développe à partir d’observations des objets physiques, de leurs structures et de leurs propriétés vers une découverte des relations entre ces propriétés par la classification, l’abstraction, la déduction mathématique et, par la suite, vers la construction des systèmes axiomatiques exprimés dans un langage mathématique formel (lettres et symboles mathématiques). Inspiré par ces travaux, Tall (2013) propose de systématiser cette vision théorique sur le développement des pensées mathématiques de toutes sortes. Son modèle part d’une étude des objets physiques, de leurs structures et de leurs propriétés qui permet aux élèves de développer des structures abstraites, de créer des concepts mathématiques. En parallèle, l’étude des opérations arithmétiques sur les nombres et de leurs propriétés permet la généralisation algébrique et la création de l’abstraction opérationnelle.

Figure 3

Les trois mondes mathématiques adaptés de Tall (2013)

Les trois mondes mathématiques adaptés de Tall (2013)

-> Voir la liste des figures

Selon Tall (2013), ces deux progressions de développement des pensées mathématiques (notamment vers l’abstraction des structures géométriques et vers l’abstraction opérationnelle) arrivées à un certain niveau donnent naissance à l’abstraction formelle: la déduction mathématique et la création des objets formels de la pensée mathématique exprimées en langage mathématique (lettres et symboles mathématiques) (Figure 3).

Les objets physiques, leurs formes géométriques et leurs propriétés ainsi que les opérations sur les nombres et leurs propriétés constituent les deux fondements de la construction de la mathématique axiomatique formelle selon Tall (2013). Pour notre part, nous constatons que dans plusieurs curriculums contemporains (par exemple au Québec) les trois mondes mathématiques sont séparés. En effet, dans le programme de formation officiel (MELS, 2001), les objets et leurs propriétés (la forme, les mesures, etc.) sont étudiés au primaire dans le cadre de l’apprentissage de la géométrie et de la mesure. Les opérations sont appliquées principalement aux nombres et aux collections d’objets et font partie de l’étude de l’arithmétique. Quant au monde de la mathématique axiomatique formelle, elle est étudiée principalement au secondaire donnant lieu à de nombreuses difficultés liées au passage des pensées plus concrètes (objets, nombres, opérations arithmétiques) à des pensées plus abstraites (déductions complexes, preuves). Dans notre expérimentation, nous avons essayé de lier plus explicitement le monde des objets physiques et leurs relations avec le monde des opérations arithmétiques pour amener les élèves au niveau de la pensée mathématique la plus abstraite possible en contexte de résolution de problèmes écrits. Bien que le but principal de l’expérimentation fût l’amélioration de la réussite en résolution des problèmes à structures additives, nos observations suggèrent l’apparition chez les élèves d’éléments de pensée qui peuvent être qualifiés comme algébriques.

4. Intervenir en salle de classe pour faire émerger la pensée algébrique: un cadre d’analyse rétrospective

Durant les 3 ans du travail expérimental de recherche et de formation, 13 enseignantes de première année (6 enseignantes) et de deuxième année (7 enseignantes) du primaire ont implanté notre approche dans leurs classes (avec un total de 216 élèves). Les enregistrements vidéo de leur enseignement nous ont permis de capter les moments clés de l’apprentissage et ainsi d’assurer un suivi plus étroit et concret auprès des enseignantes pour soutenir leur développement professionnel.

Lors de l’expérimentation, différents groupes d’élèves ont vécu des parcours différents. Toutefois, la majorité d’entre eux ont participé aux activités expérimentales durant leur deuxième année au primaire (7-8 ans). En portant un regard réflexif et rétrospectif sur l’ensemble de nos activités, nous tentons de ressortir les éléments observables qui témoignent du développement de la pensée algébrique chez les élèves qui ont participé à l’expérimentation. Nous avons analysé le parcours de ces élèves en se référant aux niveaux d’abstraction dans les trois mondes mathématiques (Tall, 2013):

  1. Objets physiques

  2. Propriétés des objets

  3. Relations entre les propriétés

  4. Déduction

  5. Formalisme mathématique

Pour notre analyse, nous avons choisi trois types d’activités développées et expérimentées par les enseignantes participantes et leurs élèves qui nous permettent d’établir des liens avec différentes étapes du développement de la pensée mathématique décrites par Van Hiele (1999) et Tall (2013):

  1. les activités de manipulation avec des objets physiques;

  2. les activités d’analyse de problèmes écrits;

  3. l’activité de résolution sur l’ordinateur.

Dans le cas de chaque type d’activité, nous avons étudié comment les trois mondes mathématiques repérés par Tall (2013), soit les structures, les opérations et le formalisme mathématique, coexistent et interagissent. Toujours en s’appuyant sur les travaux de Van Hiele et de Tall, nous avons explicité le niveau d’abstraction de la pensée mathématique possible dans le contexte de résolution de problèmes additifs simples.

Tableau 1

Les niveaux d'abstraction

Les niveaux d'abstraction

-> Voir la liste des tableaux

Dans ce qui suit, nous présentons une courte description de chaque activité, des mondes mathématiques touchés et des niveaux d’abstraction possiblement atteints. Plutôt que donner des descriptions détaillées de chaque activité observée, nous présentons quelques observations clés pour créer une image globale du parcours réalisé par les élèves et pour donner du sens à ce parcours du point de vue des trois mondes mathématiques et de la pensée algébrique. Les éléments d’enseignement et d’apprentissage vécus de façon similaire sont décrits par un seul exemple, par contre les points de divergences sont tous abordés à part.

5. Macroanalyse rétrospective

Au total, six activités ont été incluses dans notre analyse: les activités de manipulation avec des objets physiques (activités 1-3); les activités d’analyse de problèmes écrits (activités 4-5) et l’activité de résolution sur l’ordinateur (activité 6). Dans ce qui suit, nous analysons les trois types d’activités expérimentales pour en ressortir la pensée mathématique possible des élèves.

5.1 Type 1. Les activités de manipulation avec des objets physiques

Les activités basées sur les propriétés des objets physiques et les relations entre les objets font partie de la phase préparatoire, au tout début de la démarche expérimentale. Pour chaque activité, nous présentons une courte description et nous décrivons le vécu.

Activité 1a. L’enseignante, ayant en mains deux ficelles, demande aux élèves de proposer verbalement une procédure complète de comparaison qu’elle puisse exécuter pour vérifier laquelle des deux ficelles est la plus courte. Les élèves, n’ayant pas d’objets en main, doivent prononcer tous les éléments clés de la procédure de comparaison, faute de quoi l’enseignante ne réussit pas la comparaison.

Activité 1b. Les élèves doivent comparer la longueur de deux ficelles les yeux fermés en respectant la procédure de comparaison formulée lors de l’activité 1a.

Activité 2. Les élèves doivent comparer la longueur de deux objets qu’ils ne peuvent pas déplacer ou superposer (p. ex.: une jupe sur le mur droit et une cravate sur le mur gauche). Les élèves doivent représenter leur expérience de comparaison en utilisant la métaphore des ficelles (schéma) et les symboles mathématiques de comparaison (<, >, =).

Activité 3a. Ayant en mains trois bandes de papier de longueurs variées, les élèves doivent vérifier si ces bandes peuvent représenter «le total, le morceau coupé et le morceau restant». Autrement dit, si deux de ces bandes représentent la somme de la troisième. Les élèves doivent soutenir leur raisonnement par la démonstration (manipulation).

Activité 3b. Ayant en mains deux bandes de papier, les élèves doivent construire la troisième, qui correspond à la somme de deux ou à leur différence (reconstruire un morceau coupé). Ils doivent expliquer leur solution à l’aide d’un schéma.

Les activités 1, 2 et 3 se trouvent au premier niveau d’abstraction, soit les objets et leurs propriétés, car les élèves doivent manipuler des objets physiques pour répondre à la question de l’activité. L’analyse de ces activités vécues en classe montre que plusieurs liens avec (un mouvement vers) les autres niveaux de la pensée mathématique se tissent. Par exemple, lors de l’activité de comparaison de deux ficelles (activité 1), l’enseignante a demandé aux élèves comment noter mathématiquement que la ficelle rose est plus longue que la ficelle grise. Un élève a proposé la notation suivante : 1+, 2-. Il a expliqué que la ficelle 1 est plus longue et la ficelle 2 est plus courte. Apparemment, l’élève essaie d’utiliser sa compréhension des symboles d’opérations pour exprimer la relation (comparaison). D’autres élèves ont proposé d’utiliser le symbole mathématique plus grand que «>» et ils sont arrivés à la notation «1>2», ce qui apparaît mathématiquement ambigu. Un troisième élève a proposé d’utiliser les lettres R pour la ficelle rose et G pour la ficelle grise. Finalement, le groupe, guidé par l’enseignante, a construit la notation mathématique: R > G, qui ressemble à celle culturellement adoptée par la communauté mathématique.

Figure 4

L'utilisation des symboles mathématiques de comparaison

L'utilisation des symboles mathématiques de comparaison

-> Voir la liste des figures

Malgré le fait que les lettres R et G ne sont pas utilisées de façon complètement abstraite et comportent un lien sémantique avec la manipulation concrète des objets physiques (elles remplacent les couleurs identifiant les objets), cette première expérience a permis aux élèves de comprendre que les lettres peuvent être utilisées et interprétées en mathématique autrement qu’en écriture des mots.

Dans l’autre groupe, l’enseignante a amené ses élèves à constater la réversibilité de cette relation: si la ficelle rose est plus grande que la ficelle grise, la ficelle grise est plus petite que la ficelle rose et on ne peut pas écrire R=G, car les longueurs des ficelles ne sont pas égales.

Nous pouvons constater que le lien entre les relations G<R et R>G est implicite (pas verbalisé) pour les élèves, car les deux expressions sont créées à partir de l’observation. Aucune n’est déduite formellement de l’autre. On ne peut donc pas parler de déduction. Il semble toutefois qu’une déduction simple soit à portée de main dans cette situation. L’enseignante pourrait poser la question sous forme abstraite: «si nous savons que A>B, que pouvons-nous dire par rapport à B comparé à A?» Malheureusement, dans notre expérimentation, cette dernière question n’a jamais été posée ni discutée.

Lors de l’activité 2 (comparaison des objets sans déplacement), les élèves ont réalisé une déduction simple. Puisque la superposition des objets à comparer n’était pas possible, les élèves ont dû utiliser un objet intermédiaire: une corde. Ils ont coupé une corde de la même longueur que le premier objet et l’ont comparée au deuxième objet. Les élèves sont parvenus à décrire la relation directement: cravate rouge < cravate verte (Figure 5) sans mention de l’objet servant d’intermédiaire (corde). Encore une fois, la déduction n’a pas été explicitée:

Si la corde (C) a la même longueur que la cravate rouge (R) et elle est plus courte que la cravate verte (V), donc la cravate rouge est plus courte que la cravate verte.

C = R & C < V = > R < V

Il est possible que pour les élèves la corde ne joue pas le rôle de l’objet intermédiaire, mais de la représentation physique du premier objet. Le niveau de la déduction formelle ne peut donc pas être confirmé.

Figure 5

Les lettres correspondent aux couleurs des objets

Les lettres correspondent aux couleurs des objets

-> Voir la liste des figures

L’activité 3a attire l’attention des élèves à la relation «partie-partie-tout» et l’activité 3b fait appel aux opérations d’addition et de soustraction (réunir et couper) sur les objets physiques. La grande majorité des élèves observés a déduit les opérations (procédures de manipulation nécessaires) à partir de la relation donnée et était capable de reporter les procédures à l’aide de schémas. Par exemple, sachant qu’une bande représente le total et l’autre représente la partie, l’élève a construit une bande égale au total en coupant un morceau égal à la partie pour retrouver l’autre partie. Toutefois, la déduction observée n’a pas atteint le niveau du formalisme, car les élèves ont d’abord manipulé pour ensuite seulement dessiner ce qu’ils ont fait sous forme de schéma. Ils n’ont donc pas appuyé leur raisonnement sur une représentation formelle de la relation (schéma ou équation), mais sur les propriétés des objets physiques en main.

Figure 6

Image réaliste de deux ficelles: les lignes arrivent à l’extrémité de la feuille de papier

Image réaliste de deux ficelles: les lignes arrivent à l’extrémité de la feuille de papier

-> Voir la liste des figures

Lors de ces premières activités, nous avons remarqué que plusieurs représentations créées par les élèves étaient plutôt des images plus ou moins réalistes des actions vécues. La Figure 6 montre qu’à la place de représenter la relation entre les deux longueurs (schéma ou pictogramme), un élève essaie de représenter les objets tels quels. Un autre élève utilise tout l’espace disponible pour représenter une ficelle dont la longueur dépasse la longueur de la feuille. Il semble ainsi que, pour plusieurs élèves, le passage du concret à une première abstraction pictographique n’est pas évident. Par contre, la limitation de l’espace disponible (sur les feuilles de travail de plusieurs activités) encourage l’utilisation de schémas-pictogrammes plutôt que d’une image réaliste et ainsi le passage vers l’abstraction.

Plus tard, dans des activités de résolution des problèmes écrits, les images des ficelles sous forme de schémas seront utilisées comme modèles des relations additives pour y ancrer l’analyse des situations décrites.

5.2 Type 2. Les activités d’analyse de problèmes écrits

Dans le cadre de notre projet, nous avons expérimenté quatre activités d’analyse et de résolution: la situation mathématiquement incohérente (SMI), le jeu du capitaine, la résolution de problèmes et l’analyse de schémas. Nous présentons ici notre analyse des activités SMI (Savard et Polotskaia, 2017) et des activités de résolution de problèmes ordinaires, car ces deux activités comportent l’étape de l’analyse de la relation additive et l’étape de déduction.

Les activités SMI ont été créées pour stimuler les élèves à identifier la structure plutôt que la séquence d’évènements dans le contexte de petits problèmes écrits traditionnellement considérés comme des problèmes d’addition ou de soustraction. Au lieu de présenter aux élèves un texte classique, soit une description suivie par une question, nous proposons une description mathématiquement incohérente, sans question à laquelle il faut répondre immédiatement. Voici un exemple:

Activité 4. Les élèves discutent la situation suivante écrite au tableau:

Rémi a 11 coeurs à la cannelle. Il en mange 6. Il lui reste 8 coeurs à la cannelle.

Puisque les nombres sont relativement petits, les élèves doivent s’apercevoir rapidement que «ça ne marche pas». Ensemble, ils réalisent que chacun des trois nombres peut être remplacé pour faire une histoire plus cohérente. Les élèves doivent représenter la relation décrite dans l’histoire avant de proposer, pour un nombre choisi, une opération permettant de calculer la valeur cohérente avec les deux autres nombres.

Lors des expérimentations, les élèves ont réalisé plusieurs activités SMI qui présentaient des structures sémantiques variées (comparaison, retrait, addition, composition). Chaque fois, l’enseignante insistait sur l’ordre dans lequel le travail devait être effectué :

  1. Analyser la situation et la représenter par un schéma sans tenir compte des valeurs des nombres.

  2. Analyser la représentation particulière, pour chaque nombre choisi comme inconnu, pour en déduire l’opération permettant de trouver la valeur du nombre choisi.

  3. Faire le calcul et donner du sens au résultat en retournant à la situation.

  4. Analyser et comparer les trois possibilités (les trois représentations particulières et les opérations correspondantes).

Selon notre cadre d’analyse, les activités SMI se trouvent au niveau des relations, car les élèves sont invités à comprendre et à formaliser (représenter par un schéma) la relation additive entre les éléments quantitatifs de chaque situation. Elles touchent aussi le niveau de déduction, puisque les élèves doivent déduire une opération arithmétique en s’appuyant sur la représentation formelle de la relation.

L’implantation des activités SMI dans nos classes expérimentales a fait apparaître plusieurs ruptures dans les connaissances mathématiques des élèves. Premièrement, la représentation d’un ensemble d’objets (quantité d’objets) par un segment (de droite) demande une capacité d’abstraction plus avancée par rapport à une représentation de chaque objet par un jeton ou un petit cercle en correspondance terme à terme. Dans les situations où les élèves avaient le choix, plusieurs d’entre eux privilégiaient la représentation par petits cercles, celle-ci leur étant plus familière. Leur pensée restait donc au niveau des objets discrets. Pour aider les élèves à franchir la frontière discret-continu (ensemble d’objets – quantité), nous avons conçu des activités complémentaires de représentation des ensembles d’objets par des segments.

Pour stimuler l’utilisation des schémas dans les activités SMI, les enseignantes participantes ont proposé des solutions variées. Par exemple, Diana a évoqué les manipulations avec des ficelles et des bandes de papier vécues auparavant et elle a proposé d’utiliser les images de ficelles comme métaphore de la taille: si nous avons plus d’objets nous allons dessiner une ficelle plus longue. Petra a commencé à construire le schéma elle-même et, à chaque étape, elle a demandé à ses élèves de deviner ce qui était représenté. Nicole, une autre enseignante, a utilisé les cercles de papier collant au tableau et les a arrangés en ligne pour ensuite n’utiliser que les lignes (segments, Figure 7).

Figure 7

Créer des liens entre les représentations discrètes et continues

Créer des liens entre les représentations discrètes et continues

-> Voir la liste des figures

Ainsi, la majorité des élèves ont réalisé avec succès le passage «représentation des objets > représentation des quantités» (Polotskaia, 2015).

Malgré la réussite de la majorité des élèves, quelques-uns ont montré une lacune importante dans la création des liens significatifs entre les mondes mathématiques. Nos observations en classe suggèrent que ces élèves ont adopté les schémas comme des gabarits obligatoires sans lien sémantique avec la situation qu’ils essaient de représenter. La Figure 8 montre une telle représentation de la situation mettant en scène le problème de Rémi.

Figure 8

Une représentation incorrecte du problème de Rémi

Une représentation incorrecte du problème de Rémi

-> Voir la liste des figures

On peut voir dans cette image que les éléments du schéma ne représentent pas des quantités, mais qu’ils sont juxtaposés avec les nombres par hasard (probablement dans l’ordre dans lequel ces nombres apparaissent dans le texte). Ce phénomène observé dans plusieurs classes, surtout avec des élèves en difficulté, nous a fait réviser les instructions données aux enseignantes. Dorénavant, le but ultime de l’utilisation d’un schéma serait la création des liens sémantiques entre les quantités décrites dans un problème, leur rôle dans la situation et leur représentation par schéma. Nous considérons la création de tels liens comme une étape incontournable du développement de la pensée relationnelle (algébrique) qui permet l’utilisation de la relation additive (sa représentation par schéma) comme un objet de pensée abstraite mathématique.

Un changement important dans le comportement des élèves a été observé par les enseignantes. Lors des premières activités SMI, les élèves constataient rapidement que le dernier nombre dans l’histoire n’était pas correct. Dans le cas de l’histoire de Rémi, ils ont tout de suite remarqué que 8 «n’est pas bon». Un effort a été nécessaire de la part de l’enseignante pour amener les élèves à considérer les deux autres nombres. Nous pouvons penser que les élèves ont interprété l’histoire comme une séquence des évènements, comme une «opération» sur les objets pour en envisager le résultat. Vraisemblablement, ils n’ont pas considéré la «relation» entre les trois quantités. Ils n’ont donc pas questionné les deux autres nombres. Après avoir réalisé quelques activités SMI, les enseignantes ont constaté que les élèves ont questionné les trois nombres par eux-mêmes et se sont lancés à chercher les valeurs cohérentes. Nous pouvons donc espérer que les élèves commencent à considérer la relation additive dans ce contexte. Il est aussi possible que ce comportement soit un résultat du contrat didactique imposé par l’activité SMI qui demande de chercher toutes les possibilités de la situation.

La création d’une connexion entre deux mondes mathématiques a été observée dans la classe d’Anna. Anna a discuté avec les élèves de la situation de Rémi et elle a construit les trois schémas qui représentent la situation sur un grand tableau vert (Figure 9). Au moment de la recherche de la troisième opération, un élève a dit à sa voisine: Ce n’est pas comme avant. On ne doit pas additionner; on doit soustraire.

Figure 9

Les trois analyses représentées simultanément

Les trois analyses représentées simultanément

-> Voir la liste des figures

En rendant visibles les schémas et les opérations des trois analyses simultanément, l’enseignante a permis aux élèves de référer une opération à l’opération précédente. Guidés par l’enseignante, ils ont finalement constaté que la même relation additive (même histoire) peut donner lieu à trois opérations différentes. C’est probablement le moment de connexion du monde des structures et des relations avec le monde des opérations. C’est la naissance d’une liaison entre la relation additive et les opérations d’addition et de soustraction, ce qui peut signifier un niveau de complexité accru. Toutefois, ce petit épisode ne peut pas confirmer la création complète de cette liaison complexe.

Activité 5. Lors des activités de résolution de problèmes, l’enseignante présente un problème écrit traditionnel (une histoire suivie par une question) aux élèves et leur demande de l’analyser, de le représenter par un schéma et de formuler une opération arithmétique sous forme standard pour calculer la réponse. Dépendamment de la connaissance des élèves sur les procédures de calcul, le calcul de la réponse s’effectue à l’aide d’une calculatrice ou par écrit.

Voici un exemple du problème présenté aux élèves sur un Tableau blanc interactif (Figure 10).

Figure 10

Problème de spectateurs présenté sur TBI.

Problème de spectateurs présenté sur TBI.

-> Voir la liste des figures

Premièrement, l’enseignante a proposé aux élèves de déterminer si une comparaison est présente dans le problème et de choisir le type de schéma à utiliser (le schéma à un segment – pas de comparaison, ou à deux segments – comparaison). En grand groupe, les élèves ont discuté de la signification de chaque élément de données du problème et les ont associés avec l’élément du schéma. L’enseignante a utilisé trois couleurs différentes pour identifier les trois éléments de la relation (Figure 11). Elle a aussi utilisé les lettres F et G pour montrer la quantité de filles et de garçons sur le schéma.

Malgré que les élèves ont proposé une opération correcte pour trouver la réponse (49–16 = ?), l’enseignante a insisté sur la manipulation du schéma: cacher la partie connue de l’ensemble des garçons pour voir la partie équivalente à l’ensemble des filles (Figure 11).

Enseignante: Si je prends tous les garçons et que j’enlève les 16 «de plus», qu’arrive-t-il à la ligne des garçons et à la ligne des filles?

Plusieurs élèves: Elles sont égales.

Figure 11

L'enseignante cache la partie connue sur le schéma

L'enseignante cache la partie connue sur le schéma

-> Voir la liste des figures

Plusieurs variations de la gestion de l’activité de résolution ont été observées: travail en grand groupe, travail par équipe (construction de schémas), travail individuel. En tout temps, les enseignantes ont insisté sur la déduction de la phrase mathématique à partir du schéma, notamment sur l’importance de préciser l’opération et les quantités (nombres) à utiliser pour trouver la troisième quantité. Par exemple, l’expression (49–16=?) est une phrase acceptable et (49–?=16) n’est pas acceptable. Cette restriction obligeait les élèves à déduire l’opération en s’appuyant sur le schéma et sur leur compréhension de la relation additive. La calculatrice joue le même rôle restrictif (si utilisée pour le calcul), car elle n’accepte pas l’opération de type (49–?=16).

Les enseignantes opéraient sur le schéma elles-mêmes et demandaient aux élèves de le faire: passer leur doigt sur les parties à compter ensemble ou cacher une partie pour voir ce qui est inconnu. Ainsi, les deux mondes mathématiques, les structures et les opérations, s’intégraient de plus en plus chez les élèves.

Figure 12

Un schéma utilisant les mots descriptifs

Un schéma utilisant les mots descriptifs

-> Voir la liste des figures

Dans la majorité des cas, les enseignantes et les élèves ont utilisé les nombres pour noter les éléments du schéma. L’autre stratégie utilisée par les enseignantes était l’utilisation de descriptifs (Figure 12) ou de lettres (comme dans le problème des spectateurs). En travaillant seuls ou en équipes, la majorité des élèves observés réussissaient à déduire la phrase mathématique appropriée à partir d’un schéma. Toutefois, les phrases mathématiques déduites ne comportaient que des nombres. Nous pouvons suggérer que la pensée des élèves atteignait le niveau de déduction: «relation représentée → opération». Cette déduction mathématique observée dans des classes reste numérique, donc moins abstraite qu’une opération en mots ou en lettres.

5.3 Type 3. L’activité de résolution sur l’ordinateur

L’activité de résolution de problèmes à l’ordinateur (Freiman, Polotskaia et Savard, 2017) a été conçue pour stimuler et soutenir la généralisation et la formalisation de travail avec les relations et les opérations dans le contexte de résolution de problèmes écrits.

Activité 6. Les élèves doivent travailler dans un environnement informatique spécialement conçu pour résoudre des problèmes et pour identifier les problèmes qui posent des difficultés. Ensuite, les élèves rapportent leurs questions et leurs difficultés au reste de la classe. Le groupe développe une meilleure compréhension des problèmes choisis par les élèves et propose des stratégies de résolution conformes avec l’environnement informatique, ce qui est vérifié sur l’ordinateur. Lors de la prochaine session sur l’ordinateur, les élèves réessaient de résoudre des problèmes par eux-mêmes.

Afin de permettre aux élèves de travailler avec les énoncés dans lesquels les valeurs numériques ont été remplacées par les lettres (donc suscitant explicitement la production par l’élève d’une expression algébrique), une interface informatique a été conçue (Figure 13). Elle contient le titre du problème, son énoncé, les outils permettant de rédiger, de façon interactive, des phrases mathématiques standards. Initialement, l’énoncé du problème ne contient aucune valeur numérique (seulement les lettres). Si l’élève le désire, il ou elle peut obtenir la valeur numérique qui remplacera la lettre et poursuivre la résolution dans cette forme, soit numérique, soit hybride (l’élève peut «ouvrir» toutes les lettres ou juste quelques-unes). À chaque fois que l’élève ouvre une lettre, son score diminue de 10 points (initialement, ce score est égal à 100). Si le problème n’est pas résolu correctement, le score est zéro. Le but de ce jeu n’est pas d’évaluer l’élève, mais de lui permettre d’explorer le problème, de réfléchir sur la relation que le problème présente.

La Figure 13 illustre comment l’élève peut faire glisser les lettres, les nombres et les opérations pour former une phrase s-f permettant de calculer le nombre de pommes restantes. On valide la réponse en cliquant sur le bouton «Valider».

Figure 13

L'interface informatique présentant un problème à résoudre

L'interface informatique présentant un problème à résoudre

-> Voir la liste des figures

Dans le cas d’un problème à plus d’une étape, on peut réutiliser la phrase obtenue à la suite de la validation (s–f) pour formuler la prochaine phrase comme «Étape 2». À la fin de la dernière étape, on fait glisser la phrase vers la ligne de résultat avant de l’envoyer comme réponse finale (Figure 13). L’ordinateur vérifie la solution (dans notre cas, ce serait (s–f)) instantanément et informe l’élève de son résultat.

La banque de problèmes de l’environnement informatique contient 89 problèmes ayant des structures additives de toutes sortes. Chaque problème contient au moins une donnée superflue. Les élèves sont encouragés à utiliser une feuille de papier pour représenter le problème avant de construire une solution.

La première étape de l’activité présente une opportunité de déduction «relation additive → opération» dans le mode le plus formel possible dans le contexte de résolution de problèmes écrits. Si l’élève déduit la phrase mathématique en n’utilisant que des lettres, nous pouvons considérer sa pensée comme déductive, relationnelle et formelle.

Dans les classes de deuxième année, on a observé trois types de comportements devant cette tâche. Ainsi, certains élèves utilisaient les lettres pour modéliser les problèmes avec succès. D’autres élèves ont eu tendance à obtenir les valeurs numériques de chaque lettre pour composer, par la suite, une expression numérique, ce qui représente la façon de faire habituelle de la classe. Il y a finalement quelques élèves qui ont tendance à composer une phrase mathématique rapidement sans prendre le temps de réfléchir. Très peu d’entre eux construisaient des schémas. Nous constatons ainsi que pour plusieurs élèves le mode de pensée par schéma (ou par la relation additive) n’était pas devenu l’habitude de pensée dans le contexte de résolution. Il est aussi possible que malgré l’utilisation des lettres auparavant pour noter les quantités ou les longueurs, l’apparition des lettres dans le texte d’un problème a irrité ou décontenancé certains élèves, surtout au début.

Lors de la deuxième partie de l’activité, à la première discussion en salle de classe, la majorité des élèves a exprimé le désir de travailler avec des nombres plutôt qu’avec des lettres. Ils ont eu tendance à proposer des phrases mathématiques sans construction de schémas. L’enseignante a insisté sur l’ordre de travail préconisé, soit l’utilisation de schémas et de lettres. Toutefois, déjà dans la première discussion, en travaillant avec des lettres, les élèves ont facilement identifié la donnée superflue et ont proposé de ne pas ouvrir la lettre correspondante. Finalement, le groupe a réussi la modélisation par schéma en utilisant les lettres et a déduit la phrase mathématique.

Dans les deux autres séances, lors des discussions en classe, les élèves se sont montrés plus ouverts au travail avec des lettres. Ils ont réussi à placer les lettres appropriées sur les éléments du schéma (Figure 14, qui présente le schéma où m poires sont toutes les poires au début et la petite lettre d signifie les poires restantes). Cependant, une certaine ambiguïté dans l’utilisation des lettres est visible pour l’observateur. Voici un exemple tiré d’une discussion en classe.

Chercheuse [pointe sur la partie droite du schéma]: Pour trouver ce morceau sur le schéma, qu’est-ce qu’on doit faire?

E1: On prend les poires qui étaient au début et on enlève la grande partie pour voir juste les poires vendues.

Chercheuse: Comment fait-on?

E1: On cache le d. Et on enlève le m et le d.

Figure 14

Le schéma représentant le problème de poires

Le schéma représentant le problème de poires

-> Voir la liste des figures

Figure 15

La manipulation sur le schéma

La manipulation sur le schéma

-> Voir la liste des figures

La Figure 15 montre l’élève cachant les deux lettres et la partie à enlever. D’une part, dans sa première explication verbale, l’élève parle des parties de toutes les poires. D’autre part, elle cache ensuite les lettres d et m avec ses mains. L’interprétation des lettres comme éléments de graphisme coexiste avec l’interprétation des lettres comme la notation des ensembles, les poires au début m et les poires restantes d. Finalement, les élèves ont réussi à construire une phrase mathématique correcte (Figure 16) en donnant un sens approprié à chaque lettre.

Figure 16

La phrase mathématique m-d déduite par les élèves

La phrase mathématique m-d déduite par les élèves

-> Voir la liste des figures

Nous constatons que les discussions entre les élèves guidés par leur enseignante ont atteint un niveau élevé d’abstraction. Ainsi donc, l’entrée dans le monde du formalisme mathématique, notamment par l’utilisation des lettres comme éléments d’abstraction des quantités pour exprimer leur relation et pour déduire l’opération, est accessible pour plusieurs élèves. Cependant, pour que l’utilisation de ce formalisme devienne un outil privilégié de pensée des élèves lors de leur travail autonome, les trois sessions d’activité à l’ordinateur ne se sont pas révélées suffisantes.

6. Discussion: cheminement de la pensée algébrique chez les élèves

Nous avons présenté les résultats de notre macroanalyse rétrospective des activités de résolution de problèmes conçues et expérimentées lors de notre projet 2011-2014 avec des élèves âgés de 6 à 8 ans. Nous avons ainsi tenté, à l’aide du modèle des trois mondes mathématiques (Tall, 2013), de dégager les éléments de la pensée mathématique menant à la genèse de la pensée algébrique chez les élèves.

Tout d’abord, les activités de manipulation donnent lieu à la manipulation d’objets physiques, à l’étude de leurs propriétés, notamment la longueur, et de leurs structures (toutes composés de deux parties). Également, la déduction de l’opération (manipulation pour trouver le tout ou une partie) fait partie intégrante de ces activités. Les mondes des structures et des opérations coexistent dans ces premières activités.

Ensuite, les activités SMI et la résolution de problèmes donnent lieu à l’analyse de la relation additive et à la déduction par l’élève des opérations à partir de schémas. À ce stade, les élèves ne manipulent plus des objets physiques, mais le schéma comme représentant de la relation additive, objet mathématique de la pensée. Les mondes de structures et des opérations sont alors étroitement intégrés dans ces activités.

Finalement, l’activité sur l’ordinateur intègre la relation additive et les opérations ainsi que le formalisme mathématique. À ce stade, grâce aux discussions organisées à partir de l’exploration autonome d’un logiciel par l’élève, l’intégration des trois mondes mathématiques devient accessible aux élèves sous forme de construction d’un schéma en utilisant les données abstraites (en lettres) et de l’analyse de relations et de déduction de l’opération abstraite (en lettres).

Le développement de la pensée mathématique des élèves a suivi la logique des activités expérimentales. Si, dans les premières activités de manipulation, une ligne de schéma est plus une image photographique d’une ficelle et de la manipulation vécue qu’un modèle de la relation entre les objets, dans les activités de résolution de problèmes suivants, les éléments d’un schéma ne reflètent plus les objets comme tels, mais plutôt leur relation additive. Le même changement est observable dans le travail des élèves avec des lettres. Lors des activités de manipulation, les lettres servent principalement à rappeler les noms ou les couleurs des objets (V pour une cravate verte). Dans la résolution des problèmes, les descriptifs (les mots) et les lettres rappellent plutôt le rôle de la donnée dans la situation, mais y sont attachés par un lien linguistique (F pour le nombre des filles). Dans les activités à l’ordinateur, les lettres sont utilisées pour identifier les quantités de façon abstraite, sans aucun lien linguistique (m pour les poires au début de la situation). Dans ce dernier cas, les élèves sont capables de tirer des liens sémantiques à travers le modèle-schéma vers le contenu du problème et d’opérer avec des lettres en préservant le sens. En lien avec les étapes de développement de la pensée mathématique identifiées par Van Hiele (1999), les élèves ont commencé par des manipulations et ils sont arrivés à une déduction bien formelle «relation → opération».

Selon Tall (2013), la généralisation et l’abstraction des objets élémentaires de la pensée ainsi que l’intégration des structures et des opérations facilitent la compréhension des idées plus complexes et soutiennent la créativité. Pendant très longtemps, le raisonnement algébrique était vu comme une partie des mathématiques à part, opposé au raisonnement arithmétique. Aujourd’hui, plusieurs chercheurs (Davydov, 1982; Dougherty et Slovin 2004; Schmittau et Morris, 2004) perçoivent les éléments de la pensée algébrique, notamment la pensée relationnelle abstraite, comme une des pierres angulaires du développement de la pensée mathématique. Cet élément fondamental doit être exploré en profondeur dès le début de l’apprentissage scolaire et doit grandir au fur et à mesure de la complexification des objets de la pensée mathématique. Nous suggérons de modifier et d’ajuster le modèle de Tall de façon suivante : dès le début de l’apprentissage, il faut assurer la coexistence, le codéveloppement et l’intégration des trois mondes mathématiques. La Figure 17 montre que, conformément au modèle de Tall (2013), les mondes des structures et des opérations, superposés et intégrés dès le début de la scolarisation pour donner lieu aux premières déductions et au formalisme mathématique, peuvent stimuler le développement précoce de la pensée algébrique.

Figure 17

Les trois mondes mathématiques intégrés donnant lieu à la pensée algébrique précoce

Les trois mondes mathématiques intégrés donnant lieu à la pensée algébrique précoce

-> Voir la liste des figures

7. Conclusion

Nous avons cherché à démontrer qu’au tout début de l’apprentissage des mathématiques, il est possible de proposer aux élèves âgés de 6 à 8 ans des activités dans lesquelles les trois mondes mathématiques se touchent. Dans nos expérimentations, les activités de manipulations avec des objets physiques ont donné lieu à la construction des relations entre les grandeurs, à la déduction, bien que supportée par la manipulation, et à l’utilisation du symbolisme mathématique formel.

Lors des activités de résolution, les élèves ont démontré un niveau d’abstraction accru, notamment par l’utilisation de la modélisation des relations à l’aide de schémas (schémas) pour en déduire l’opération arithmétique. L’activité de résolution sur l’ordinateur a permis d’observer les élèves utiliser des lettres dans leur pensée mathématique ainsi que dans le processus de modélisation et de déduction.

Dans la mathématique formelle, le concept de la «relation additive» n’est pas reconnu comme une «définition», au même titre que la loi «pour trouver une partie du total, il faut enlever l’autre partie du total» n’est pas considérée comme un «axiome». Toutefois, dans le contexte de notre expérimentation, il est logique de proposer que ces éléments de la pensée mathématique (centraux dans le cadre de notre projet) aient été implicitement exploités par les enseignantes et les élèves comme définition et axiome.

Notre recherche, qui s’aligne avec les expérimentations réalisées dans d’autres pays (Mikulina, 1991; Iannece et al., 2009; Schmittau et Morris, 2004), montre que les élèves peuvent étudier conjointement les relations et les opérations et développer une compréhension de plus en plus abstraite, ou algébrique. Une compréhension algébrique des problèmes et des situations élémentaires, à son tour, peut devenir un outil de pensée indispensable dans l’étude des objets mathématiques plus complexes, y compris les objets mathématiques algébriques.