Quelles connaissances et quels raisonnements en arithmétique favorisent l’entrée dans l’algèbre? Which arithmetic knowledge and reasoning facilitate students’ entry into algebra? ¿Cuáles conocimientos y cuáles razonamientos en aritmética favorecen la entrada al álgebra?

Résumé

Nous nous inscrivons dans le courant Early Algebra en soutenant que des connaissances et des raisonnements développés par les élèves en début de collège en France (11-12 ans) en arithmétique peuvent faciliter la transition de l’arithmétique à l’algèbre ou au contraire y faire obstacle. Nous définissons des critères pour analyser le rapport personnel des élèves à l’arithmétique en début de 5^e (12 ans), avant l’entrée dans l’algèbre. En nous plaçant dans le cadre de la théorie anthropologique, nous définissons ensuite des praxéologies (Chevallard, 1999) pour repérer la signification et le rôle que les élèves donnent à l’égalité, aux expressions numériques, aux propriétés des opérations, dont la distributivité, et au raisonnement analytique. Nous présentons l’évaluation de début de 5^e conçue dans ce cadre et analysons les réponses des élèves, puis ouvrons des perspectives sur les conditions d’un enseignement favorisant l’entrée dans l’algèbre.

Mots-clés :

• entrée dans l’algèbre,
• arithmétique,
• évaluation,
• égalité,
• expression algébrique

Abstract

Our research comes under the Early Algebra current, upholding that the arithmetic knowledge and reasoning developed by early middle-school students in France (11–12 years old) can facilitate, or conversely raise obstacles to, the transition from arithmetic to algebra. We define criteria for analyzing beginning cinquième (Canadian secondary two, 12 year old) students’ personal relationships to arithmetic before they start algebra. Drawing on anthropological theory, we then define praxeologies (Chevallard, 1999) for identifying the meaning and role that students assign to equality, numeric expressions, properties of operations including the distributive property, and analytical reasoning. We then present the beginning of cinquième evaluation designed in this context and examine the students’ answers, before exploring the instructional conditions that could facilitate students’ entry into algebra.

Keywords:

• entry into algebra,
• arithmetic,
• evaluation,
• equality,
• algebraic expression

Resumen

Nos adscribimos a la corriente Early Algebra sosteniendo que los conocimientos y los razonamientos desarrollados en aritmética por los alumnos que comienzan el nivel colegial en Francia (11 a 12 años) pueden facilitar la transición desde la aritmética al álgebra, o por el contrario, generar obstáculos a este paso. Definimos criterios para analizar la relación personal con la aritmética de los alumnos que comienzan el quinto grado (12 años), antes de entrar en el álgebra. Dentro del marco de la teoría antropológica, definimos a continuación praxeologías (Chevallard, 1999) para captar el significado y el rol que los alumnos entregan a la igualdad, a las expresiones numéricas, a las propiedades de las operaciones, entre ellas distributividad y al razonamiento analítico. Presentamos la evaluación concebida en este cuadro y aplicada al inicio del quinto grado y analizamos las respuestas de los alumnos, para después abrir las perspectivas acerca de las condiciones de una enseñanza que facilite la entrada al álgebra.

Palabras clave:

• entrada al álgebra,
• aritmética,
• evaluación,
• igualdad,
• expresión algebraica

1. Introduction

Depuis 1995, l’équipe de chercheurs en didactique des mathématiques impliqués dans le projet «Pépite» (Delozanne et al., 2010; Grugeon-Allys et al., 2012; Pilet, 2015) conçoit et diffuse des outils pour développer des pratiques d’évaluation diagnostique et de régulation pour l’enseignement en algèbre élémentaire. Ces outils concernent l’enseignement de l’algèbre pour des élèves de 13 à 16 ans (4^e à 2^de), c’est-à-dire après l’introduction du symbolisme algébrique. Plus récemment, dans le cadre du Lieu d’Education Associé «Pratiques d’évaluation en calcul numérique et littéral» (LéA Pécanumeli[1]), organisant un travail collaboratif entre enseignants et chercheurs, à la demande des enseignants, nous avons commencé à concevoir et à développer de tels outils avant l’introduction du symbolisme algébrique et son enseignement en 5^e (12 ans) (Horoks et Pilet, 2015). L’enjeu est de faire état du développement des connaissances et des raisonnements déjà utilisés par les élèves en arithmétique favorisant ou non l’entrée dans l’algèbre, que nous définissons comme l’introduction à la modélisation pour résoudre les problèmes du domaine algébrique (Chevallard, 1985, 1989).

Nous prenons en compte le courant Early Algebra (Kieran et al., 2016) qui vise à offrir aux élèves des opportunités pour soutenir la transition de l’arithmétique à l’algèbre dès l’école primaire et le début du collège. Quels sont les connaissances et les raisonnements développés par les élèves en début de collège en arithmétique qui peuvent faciliter la transition de l’arithmétique à l’algèbre ou au contraire y faire obstacle? À partir de quels critères et de quelles tâches les repérer? Comment analyser les réponses des élèves afin de pouvoir exploiter les informations recueillies?

Pour répondre à ces questions, nous rappelons d’abord les deux principaux courants développés pour interroger la transition entre l’arithmétique et l’algèbre. Nous identifions ensuite des critères d’analyse du développement des connaissances et des raisonnements déjà utilisés en arithmétique et qui sont liés à des concepts cruciaux pour l’entrée dans l’algèbre (égalité, expression numérique, etc.). Nous caractérisons ensuite des praxéologies (Chevallard, 1999) pour repérer la signification et le rôle que les élèves donnent à l’égalité, aux expressions numériques, aux propriétés des opérations dont la distributivité et au raisonnement analytique. Nous présentons l’évaluation conçue pour le niveau 5^e et soumise à un ensemble d’élèves et analysons les réponses des élèves. Pour terminer, nous discutons du potentiel des résultats obtenus pour organiser des pistes d’enseignement d’entrée dans l’algèbre et des perspectives de recherche.

2. Continuité ou discontinuité: deux points de vue sur la transition entre l’arithmétique et l’algèbre

Les travaux relatifs à la transition entre l’arithmétique et l’algèbre s’organisent en deux points de vue. Certains (Vergnaud, 1988; Rojano, 1989; Kieran, 1992) considèrent que l’algèbre se construit en rupture avec l’arithmétique. D’autres, s’inscrivant plus récemment dans le courant Early Algebra (Kieran et al. 2016; Radford, 2014), considèrent que la transition doit être négociée dès l’école primaire.

2.1 Travaux privilégiant une rupture entre arithmétique et algèbre

Certains travaux prônent une discontinuité entre l’arithmétique et l’algèbre (Grugeon, 1997). Vergnaud (1988) parle de double rupture épistémologique entre l’arithmétique et l’algèbre:

D'une part, l'introduction d'un détour formel dans le traitement des problèmes habituellement traités intuitivement, d'autre part, l'introduction d'objets mathématiques nouveaux comme ceux d'équation et d'inconnue, de fonction et de variable […].

p. 189

La première rupture concerne le raisonnement pour résoudre les problèmes. Contrairement au raisonnement arithmétique, qui part du connu pour calculer les inconnues en lien avec le contexte, le raisonnement algébrique consiste à représenter les relations entre les données et les nombres non connus du problème et à utiliser un traitement formel pour le résoudre.

La seconde rupture concerne l’évolution du statut des objets. En arithmétique, le signe d’égalité est majoritairement utilisé comme annonce de résultat pour effectuer les calculs (souvent de gauche à droite), alors que le traitement des expressions algébriques repose sur le statut d’équivalence de l’égalité. De plus, contrairement aux habitudes de calcul en arithmétique sur les expressions numériques, une expression algébrique peut conserver un signe opératoire après réduction des calculs, x+1 par exemple. Cette rupture avec les pratiques arithmétiques, qui peut constituer un obstacle durable chez les élèves, est identifiée par de nombreux chercheurs comme le dilemme process-product (Davis, 1975 dans Kieran, 1992) ou l’acceptance of lack of closure (Collis, 1974 dans Kieran, 1992).

Il en va de même pour les équations. Filloy et Rojano (1989) évoquent une coupure entre l’arithmétique et l’algèbre dans la résolution d’équations. Alors que la résolution d’équation du type ax+b=c peut se faire en utilisant des raisonnements arithmétiques qui consistent à inverser les opérations, et donc à raisonner uniquement à partir de quantités connues, la résolution d’équations du type ax+b=cx+d, pour des valeurs des coefficients conduisant à une solution rationnelle non décimale, repose sur un raisonnement algébrique. Un tel raisonnement nécessite d’opérer sur l’inconnue et s’appuie sur les propriétés de conservation de l’égalité. Vergnaud (1988) souligne que trop souvent les enseignants considèrent que l’algèbre commence avec l’introduction des équations, des fonctions et la manipulation des expressions littérales, alors que dès l’école primaire certaines activités relèvent de l’algèbre:

Pourtant, certains modes de représentation et d’écriture comme les égalités à trous, utilisées dès les premières classes de l’école élémentaire, ressemblent étrangement à l’algèbre. Et si l’on considère comme étant de nature algébrique, la tâche qui consiste à mettre un problème en représentation, c’est-à-dire à extraire d’un problème ou d’une situation les relations pertinentes, à en fournir un modèle symbolique, puis à traiter les relations ainsi représentées à l’aide d’une syntaxe propre au système symbolique choisi, alors l’algèbre commence, on peut commencer, dès l’école l’élémentaire.

p. 189

Pour Kieran (1992), étant donné que l’algèbre reprend des symboles comme les lettres ou le symbole d’égalité déjà utilisés en arithmétique, mais avec des significations différentes, la transition marque une fausse continuité. L’utilisation de nouveaux objets et le développement du raisonnement algébrique pour résoudre des problèmes marquent une discontinuité entre l’arithmétique et l’algèbre.

2.2 Le courant Early Algebra et le développement de la pensée algébrique

Le courant Early Algebra est né dans les années 2000 avec une volonté de rendre accessible à de jeunes élèves (6 à 12 ans) certains aspects de l’activité algébrique pour développer ce que les chercheurs de ce courant désignent sous le nom de «pensée algébrique». Radford (2014) définit la pensée algébrique en situation de résolution de problèmes à partir de trois caractéristiques, résumées ainsi par Kieran et al. (2016):

(a) indeterminacy: unknown numbers are involved in the given problem, (b) denotation: the indeterminate numbers are named or symbolized in various ways such as with gestures, words, alphanumeric signs, or some combination of these, and (c) analyticity: the indeterminate quantities are treated as if they were known numbers.

p. 5

L’analycité repose sur la déduction des résultats à partir de propriétés et s’oppose aux raisonnements arithmétiques décrits par Radford comme des raisonnements de type tâtonnement ou essai/erreur: «trial-and-error methods fail to satisfy the condition of analyticity» (Radford, 2014, p. 260). Radford propose des situations de généralisation basées sur des motifs (patterns) pour montrer qu’une pensée algébrique peut émerger chez des élèves jeunes. Dans ces situations, les élèves mettent en oeuvre un raisonnement analytique et expriment le nombre d’éléments à une étape de la séquence en fonction du numéro de cette étape.

Dans leur synthèse des travaux relevant de l’Early Algebra, Kieran et al. (2016) distinguent quatre thèmes principaux pour ce nouveau domaine: (1) la généralisation liée aux activités de motifs (patterns) numériques et géométriques, (2) la généralisation liée aux propriétés des opérations et aux structures numériques, (3) la représentation des relations entre les quantités et (4) l’introduction de la notation alphanumérique. Nous revenons ici sur les trois premiers thèmes.

Radford montre que dans des situations de généralisation et sous certaines conditions d’enseignement de jeunes élèves (dès le grade 2) peuvent rentrer dans une pensée algébrique sans aucun symbolisme alphanumérique. Les gestes associés à des verbalisations jouent un rôle primordial dans l’accompagnement des élèves pour développer l’analycité. En ce qui concerne notre problématique, repérer la présence ou non de raisonnement analytique en résolution de problèmes (généralisation) est un indicateur pertinent pour évaluer la disposition des élèves à entrer dans l’algèbre.

Dans le contexte arithmétique, dans la résolution de problèmes, mais aussi dans des calculs, les élèves peuvent développer le statut d’équivalence du signe d’égalité (Carpenter et al., 2003; Fujii, 2003) et généraliser des propriétés des opérations, notamment celle de distributivité. Cela permet aux élèves de considérer une opération non pas uniquement comme un processus, mais aussi comme un objet mathématique (Kieran et al., 2016). Nous pointons aussi le rôle joué par les propriétés des opérations lors de réécritures impliquées dans du calcul réfléchi (Butlen et Pézard, 2007). Le calcul réfléchi vise à transformer certains calculs en calculs plus économiques et efficaces par le biais d’une réécriture d’expressions numériques, à l’aide de propriétés des nombres et des opérations, comme 11×8=10×8+8 (distributivité de la multiplication par rapport à l’addition).

De plus, pour Kieran et al. (2016), l’enseignement de l’algèbre est basé sur la capacité à représenter des relations entre quantités. Nous ajoutons que le fait d’exprimer des relations entre quantités repose sur des conversions entre registres de représentation sémiotique (Duval, 1993) qui peuvent être travaillées dès l’école primaire à l’occasion de la résolution de problèmes, notamment dans des cas de non-congruence sémantique (Ibid.).

Ainsi, les recherches portant sur la transition entre l’arithmétique et l’algèbre convergent vers l’idée qu’il y aurait des potentialités à travailler des objets mathématiques à la frontière entre l’arithmétique et l’algèbre dès l’école primaire, avec l’hypothèse que cela faciliterait l’entrée dans l’algèbre.

3. Des critères pour analyser l’activité arithmétique avant l’entrée dans l’algèbre

Nous présentons le cadre d’analyse proposé par Grugeon (1997) pour repérer les connaissances et les raisonnements mobilisés par des élèves lors de la résolution d’une tâche de généralisation et de preuve donnée à l’entrée en 3^e et de début de lycée. L’enjeu est de transposer cette approche afin de définir des critères pour analyser l’activité arithmétique avant l’entrée dans l’algèbre en résolution de problèmes. Nous nous appuyons sur une synthèse de travaux de didactique portant sur l’entrée dans l’algèbre.

3.1 Un exemple d’analyse de réponses pour dégager des critères

Prenons le problème de généralisation et de preuve suivant, dit du «prestidigitateur» (Grugeon, 1997):

«Tu penses un nombre, tu ajoutes 8, tu multiplies par 3, tu retranches 4, tu ajoutes ton nombre, tu divises par 4, tu ajoutes 2, tu soustrais ton nombre: tu as trouvé 7. L'affirmation est-elle vraie? Justifiez votre réponse»

p. 184

Ce programme de calcul donne toujours le nombre 7, pour tout nombre initial, ce qu’il faut prouver.

Ce problème a été posé à des lycéens de filière technologique générale provenant d’un enseignement professionnel. Leur rapport personnel à l’algèbre (Chevallard, 1999) est issu d’un apprentissage dans plusieurs institutions faisant vivre des rapports institutionnels à l’algèbre différents de celui attendu en lycée technologique et qui, pour certains, laissent vivre des raisonnements arithmétiques en dehors de leur domaine de validité.

À partir d’une analyse a priori (Artigue, 1990), Grugeon (1997) catégorise les réponses d’élèves envisageables (présentées dans les tableaux 1 et 2) et, notamment, les raisonnements non idoines compte tenu de l’activité mathématique attendue à ce niveau scolaire. Nous organisons l’analyse a priori à partir de trois entrées: le raisonnement pour réaliser une preuve, le type d’écriture utilisé pour représenter le programme de calcul et les statuts des objets mobilisés et des traitements réalisés.

Tableau 1

Expressions numériques lors de la résolution

Tableau 1 (suite)

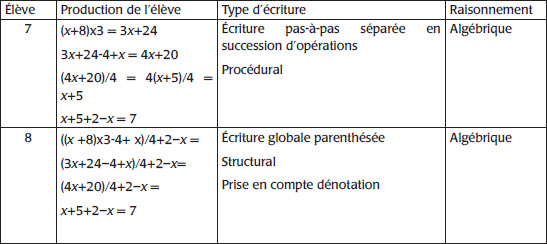
Tableau 2

Expressions symboliques lors de la résolution

Tableau 2 (suite)

Le raisonnement attendu à ce niveau scolaire au problème du prestidigitateur est un raisonnement algébrique (réponses 7 et 8 du tableau 2) s’appuyant sur la production d’une expression générale du programme de calcul ((x+8)×3-4+x)/4+2–x, puis sur la transformation de l’expression produite pour prouver que ce programme est égal à 7 pour tout nombre. D’autres raisonnements erronés sont envisageables: un raisonnement arithmétique à partir d’un ou de plusieurs exemples numériques (réponses 1 à 4) ou un raisonnement analytique (réponses 4, 5 et 6). En effet, l’élève de la réponse 4 propose un raisonnement analytique, car il considère 5 comme un nombre ayant un caractère générique (Balacheff, 1982) et formule que «multiplier un nombre par 3 et ajouter ce nombre, le tout à diviser par 4 correspond à ce nombre. Quand on soustrait ce nombre, il reste 0. Le calcul correspond donc à (8×3-4)/4+2, soit 7». Les réponses 5 et 6 proposent un raisonnement analytique à partir de plusieurs lettres pour désigner des nombres non connus, résultats intermédiaires du programme de calcul.

L’écriture attendue pour le résultat du programme de calcul est l’expression algébrique globale parenthésée ((x+8)×3-4+x)/4+2–x prenant en compte les priorités opératoires (réponse 8). Dans cette expression, x est une variable représentant n’importe quel nombre. La transformation de l’expression en appui sur la propriété de distributivité met en jeu l’égalité comme relation d’équivalence. Cependant, d’autres écritures, présentées plus loin, sont possibles (réponses 1 à 7). Ces écritures dépendent du rapport personnel construit à l’objet «programme de calcul» dans les institutions scolaires et de la conceptualisation des objets mathématiques rencontrés: ici, un programme de calcul en lien avec les expressions numérique ou algébrique, les statuts des lettres et du signe d’égalité. En particulier, les expressions peuvent indiquer les résultats des étapes d’un calcul pas-à-pas séparé ou non. Les chercheurs (Chevallard, 1990; Ruiz-Munzon et al., 2012; Douek et Morselli, 2012) attribuent au programme de calcul un rôle central pour donner des raisons d’être aux expressions au cours d’un enseignement préalgébrique ou algébrique.

Les réponses 1 et 2 s’appuient sur des suites de calculs numériques pas à pas, séparés (réponse 2) ou non (réponse 1), pour trouver le résultat du programme de calcul à partir d’une conception procédurale des expressions numériques qui favorise le signe d’égalité comme annonce de résultat ou comme «étiquette» pour indiquer le résultat et une nouvelle étape du calcul (cf. section 3.3). Il en est de même pour les réponses 5 et 6.

La réponse 3 relève d’une expression numérique non parenthésée et la réponse 4 d’une expression numérique parenthésée. La réponse 5 utilise plusieurs lettres pour désigner les résultats intermédiaires du programme de calcul dans une écriture pas-à-pas enchaînée incorrecte vis-à-vis de l’égalité. La réponse 6 représente les résultats intermédiaires dans une écriture pas-à-pas séparée, l’égalité indiquant une annonce de résultat, mais les transformations mises en oeuvre mettent en évidence le dilemme processus/résultat. La réponse 8 s’appuie sur des expressions algébriques indiquant les résultats des étapes intermédiaires et mobilisant le signe d’égalité comme annonce de résultat.

Ce type d’analyse donne accès à des informations sur les expressions produites, algébriques comme numériques, et sur la nature du raisonnement, algébrique, analytique ou arithmétique. Nous présentons maintenant les critères utilisés dans cet article et leurs valeurs possibles que nous retenons comme indicateurs pour analyser le rapport de l’élève à l’arithmétique avant l’entrée dans l’algèbre.

3.2 Statut du signe d’égalité

Le signe d'égalité a un double statut. Il peut désigner soit l'annonce d'un résultat, soit une relation d'équivalence. En arithmétique, le signe d'égalité est utilisé de façon dominante comme signe d'annonce de résultat (4+3=7). Dans des tâches spécifiques de calcul réfléchi, le signe d’égalité intervient comme relation d’équivalence avec la réécriture d’expressions numériques ayant la même valeur, en appui sur les propriétés des opérations et de la numération (47+14=47+3+11=50+11=61; 238=20×8+3×8 (distributivité)).

L’égalité peut aussi indiquer les étapes d’un programme de calcul et peut conduire à des écritures incorrectes. Par exemple, l’écriture 50-24=26+12=38 ne respecte pas la symétrie et la transitivité de l'égalité. Un manque de travail sur l’égalité comme relation d’équivalence peut être un obstacle à l’entrée dans l’algèbre, voire être un vecteur d’inégalités scolaires si l’institution le laisse implicite et à la charge des élèves (Castela, 2008; Rochex et Crinon, 2011). Le statut de l’égalité mobilisé par l’élève est un critère pertinent pour évaluer les potentialités d’arrimage de l’arithmétique à l’algèbre.

3.3 Dénotation des expressions et réécriture à partir des propriétés des opérations

La notion de dénotation d’une expression algébrique a été définie par Drouhard (1992) en référence à la distinction établie par Frege (1971) entre sens (Sinn) et dénotation (Bedeutung). Par exemple, les expressions numériques 47+14, 47+3+11, 50+11 mettent en jeu des signes différents, mais réfèrent à un même nombre (61), leur dénotation. En revanche, les expressions n'ont pas le même sens puisqu'elles ne relèvent pas du même point de vue et vont donner lieu à des stratégies efficaces de calcul et la mobilisation de propriétés opératoires. Le calcul réfléchi ou le calcul algébrique repose sur la transformation d'expressions à dénotation fixe. Leur réécriture s’appuie sur le sens des expressions et sur les propriétés des opérations et des nombres. Le statut du signe d'égalité est nécessairement une relation d'équivalence. La réécriture des expressions s’appuie sur les propriétés des nombres et des opérations (commutativité, associativité et distributivité de la multiplication par rapport à l’addition et à la soustraction). Constantin (2017) montre que la distributivité, utilisée implicitement en primaire, est un savoir qui unifie des connaissances numériques et algébriques. Il n’est pas suffisamment pris en charge au moment de l’introduction formelle de l’algèbre au collège alors qu’il joue un rôle essentiel dans la transition entre l’arithmétique et l’algèbre.

La capacité à raisonner en passant d’une écriture à une autre tout en s’assurant de conserver leur dénotation peut être travaillée dès l’école primaire. La prise en compte de la dénotation des expressions numériques lors de leur transformation dans un calcul étant un critère pour l’entrée dans l’algèbre.

3.4 Caractères procédural et structural d’une expression

Dans la section 3.2, le caractère structural d’un concept apparaît comme un élément clé pour développer l’usage des propriétés des opérations lors de leur réécriture. Rappelons que Sfard (1991) propose un modèle de développement conceptuel aboutissant à une réification des expressions symboliques. Ce modèle s'appuie sur une distinction entre les caractères structural et procédural des concepts mathématiques. Sfard (1991) distingue concepts et conceptions, les conceptions étant définies comme des représentations ou des associations évoquant des notions mathématiques abstraites. Les notions mathématiques abstraites peuvent être conçues de deux façons différentes: comme des processus (procédural) ou comme des objets (structural), ces deux caractères cohabitant lors de l’activité mathématique. Par exemple, en ce qui concerne le calcul de l’expression numérique 2×4+5, deux représentations du calcul sont envisageables, l’une qui privilégie le caractère structural de l’expression 2×4+5=8+5=13 appuyé sur les priorités opératoires, l’autre le caractère procédural 2×4=8; 8+5=13. Selon Sfard (1991), dans l’apprentissage d’un concept, l’élève mobilise souvent en premier son caractère procédural avant son caractère structural. La prise en compte par les élèves du caractère procédural ou structural est un critère pertinent pour étudier l’appréhension des expressions numériques par les élèves dans des contextes variés de calcul ou de production d’expressions pour représenter un problème.

En conclusion, les critères suivants permettent d’analyser l’activité arithmétique avant l’entrée dans l’algèbre: statut du signe d’égalité, prise en compte de la dénotation des expressions numériques en lien avec les propriétés des opérations, caractère d’une expression numérique. Le statut du raisonnement, notamment analytique, développé dans la section 2. est un autre critère que nous prenons en compte. L’usage de l’égalité comme relation d’équivalence et de la lettre comme variable, la transformation d’expressions numériques à dénotation fixe, la flexibilité entre les caractères structural et procédural d’une expression numérique, l’usage des propriétés des opérations et en particulier de la distributivité et l’usage d’un raisonnement analytique sont autant d’indicateurs d’une entrée adaptée dans l’algèbre. Ils fondent le bloc théorique des praxéologies qui caractérisent un rapport idoine à l’arithmétique favorable à l’entrée dans l’algèbre.

4. Quelles praxéologies pour analyser l’activité mathématique des élèves avant l’entrée dans l’algèbre?

Nous présentons maintenant comment nous avons sélectionné des types de tâches pour concevoir une évaluation diagnostique visant à repérer les connaissances et les raisonnements d’élèves en 5^e n’ayant pas entamé l’apprentissage du calcul littéral.

4.1 Un cadre de référence pour une évaluation diagnostique au service des apprentissages des élèves

Nous nous situons dans le cadre de la théorie anthropologique du didactique (Chevallard, 1999). Nous prenons en compte le développement des connaissances construites par les élèves dans une institution donnée (ici la classe de 5^e en France) au regard de ce qui leur a été enseigné depuis l’école primaire et en début de collège, c’est-à-dire relativement aux praxéologies mathématiques (Chevallard, 1999) impliquées dans la résolution des problèmes proposés dans l’institution[2]. Une praxéologie mathématique met en jeu conjointement un bloc praxique et un bloc théorique. Au niveau des praxéologies ponctuelles, le bloc praxique est constitué d’un type de tâches et d’une technique qui permet de réaliser ce type de tâches; le bloc théorique est constitué d’un discours technologique qui décrit, explique, justifie la technique, lui-même soutenu par une théorie plus ou moins développée et explicite. Les praxéologies ponctuelles s’organisent en praxéologies locales puis globales.

Nous étudions les praxéologies mises en oeuvre par les élèves lors de la résolution de tâches au regard des critères présentés dans la section 3.3. Nous proposons une évaluation pour situer l’activité arithmétique des élèves lors de la résolution de types de tâches travaillés à l’entrée en 5^e.

4.2 Types de tâches, technologie et théorie idoines pour étudier l’arrimage de l’arithmétique à l’algèbre

Préalablement, nous avons rappelé les types de tâches spécifiques de l’algèbre dans des contextes variés comme ceux de généralisation, de modélisation ou de preuve. Chevallard (1985, 1989, 1990) a étudié des difficultés liées à la transition arithmétique/algèbre dans l’enseignement d’un point de vue historique et épistémologique. Pour lui, la modélisation dans les cadres numérique et fonctionnel est spécifique à l’activité algébrique à tous les niveaux scolaires, dans différents contextes intra et extramathématiques et en rupture avec l’arithmétique. Chevallard met aussi en évidence l’importance de l’étude de l’ensemble des nombres comme un support pour définir des situations amenant les élèves à conjecturer des propriétés arithmétiques, à les généraliser, puis à les prouver en dégageant un nouvel outil, l’algèbre. D’autres recherches (Bednarz et al., 1996; Douek et Morselli, 2012; Radford, 2014) ont montré les potentialités des situations de généralisation, souvent sous la forme de motifs (patterns), pour favoriser l’entrée dans l’algèbre.

À partir des critères précédemment définis, nous listons un ensemble de types de tâches du domaine arithmétique pour repérer le développement de connaissances et de raisonnements qui peuvent faciliter l’entrée dans l’algèbre:

• Généraliser un motif (pattern): l’enjeu est d’évaluer si les élèves s’engagent dans un raisonnement analytique ou non et de repérer quels types de symbolisation (alphanumérique ou non) ils utilisent pour représenter les relations entre nombres connus et indéterminés.

• Résoudre des problèmes arithmétiques dans le domaine numérique ou dans celui des grandeurs: l’enjeu est d’étudier les expressions numériques produites pour représenter le problème, le caractère privilégié (procédural et/ou structural) des expressions et le statut du signe d’égalité mis en jeu, en lien avec la prise en compte de la dénotation des expressions numériques.

• Effectuer un calcul réfléchi: l’enjeu est aussi de repérer le statut du signe d’égalité mis en jeu, en lien avec la prise en compte de la dénotation des expressions, le caractère procédural ou structural des expressions privilégié lors de leur réécriture, la prise en compte des propriétés des opérations et des nombres, en particulier de la distributivité de la multiplication par rapport à l’addition.

• Calculer une expression numérique mettant en jeu les priorités opératoires et la distributivité.

• Associer des expressions numériques de structures différentes.

Un rapport idoine à l’arithmétique favorable à l’entrée dans l’algèbre est caractérisé par les praxéologies généraliser, résoudre et calculer, qui reposent sur le bloc théorique défini dans la section 3.

4.3 Des indicateurs pour évaluer des productions d’élèves

Nous analysons ici les techniques mises en jeu par les élèves pour résoudre chaque tâche à partir de leur analyse a priori. Nous présentons pour chaque critère les indicateurs utilisés pour décrire les éléments technologico-théoriques soutenant les techniques:

• Nature des signes: lettre, mot, dessin, nombre;

• statut de l’égalité: statut d’équivalence/annonce de résultat/étiquette;

• dénotation des expressions numériques: prise en compte ou non;

• caractère d’un concept: procédural et/ou structural;

• raisonnement: arithmétique/analytique (dans la résolution de problèmes de généralisation).

Nous opérationnalisons ensuite cette méthodologie pour une évaluation en classe de 5^e.

5. Des évaluations avant l’entrée dans l’algèbre en début de 5^e

5.1 Les évaluations dans les programmes et dans les manuels

Les programmes et les manuels donnent très peu d’outils aux enseignants pour évaluer les connaissances de leurs élèves avant l’entrée dans un nouveau thème et en particulier pour l’algèbre. En effet, parmi ceux analysés, seul le manuel de l’édition Triangle chez Hatier (2006) propose de «Faire le point» avant le chapitre sur le calcul littéral (figure 1).

Figure 1

«Je fais le point sur mes connaissances» du manuel Triangle (5^e éd.), Hatier 2006, p. 113

Plusieurs types de tâches listés dans la section 4.2 sont convoqués dans cet extrait de manuel. L’exercice 1, qui relève du type de tâches «calculer une expression numérique en ligne», permet de déterminer si l’élève prend en compte la structure de l’expression numérique et s’il s’appuie sur les propriétés des opérations pour savoir dans quel ordre effectuer le calcul. L’exercice 2 permet aussi de savoir si les élèves interprètent correctement la structure des expressions numériques. L’exercice 3.a permet de déterminer si les élèves savent exprimer la longueur d’un segment représentée par une figure codée en une expression numérique. Enfin, l’exercice 3.b peut donner des informations riches sur les types d’écritures utilisés par les élèves (cf. section 3.1) et donc sur leur capacité à mobiliser le caractère structural des expressions.

Cette évaluation présente donc des potentialités pour repérer si les élèves privilégient un des deux caractères procédural ou structural des expressions numériques et quels types d’écritures numériques ils utilisent. Cependant, elle ne permet pas de repérer si les élèves s’engagent dans des raisonnements analytiques. De plus, nous nous interrogeons sur l’utilisation en classe qui peut en être faite par les enseignants si les critères d’analyse ne leur sont pas explicités. Cette évaluation a-t-elle une fonction formative ou bien est-elle exploitée uniquement quantitativement, en termes de réponse correcte ou incorrecte?

5.2 Analyse a priori d’une évaluation à l’entrée en 5^e

Nous avons conçu cette évaluation avec des enseignants de collège dans le cadre du LéA Pecanumeli sur les pratiques d’évaluation des enseignants en calcul algébrique et littéral. Les enseignants ont fait des propositions de tâches que nous avons négociées avec eux. L’ensemble des tâches retenues devait faire partie des types de tâches spécifiées dans la section 4.2, mais aussi répondre aux contraintes des enseignants, notamment le temps de passation et l’insertion de l’évaluation dans leurs séquences d’enseignement.

5.2.1 Les tâches

Les tâches diagnostiques retenues sont présentées en figure 2. Il est prévu de faire passer le test une fois les priorités opératoires travaillées en début de 5^e, et avant l’introduction des expressions algébriques.

Figure 2

Les tâches retenues

Les tâches retenues suite à la négociation avec les enseignants recouvrent en partie les types de tâches (tableau 3) définis pour étudier l’arrimage entre l’arithmétique et l’algèbre. Ils n’ont pas choisi de tâches de calcul parce qu’elles avaient été travaillées par ailleurs. La tâche de généralisation (exercice 1) a fait l’objet d’une discussion spécifique avec les enseignants. En effet, en France, les élèves ne rencontrent jamais de telles tâches et les enseignants craignaient que leurs élèves ne produisent rien. Après avoir discuté avec eux des critères d’analyse, nous avons insisté sur le rôle de cette évaluation: repérer si ce que produisent les élèves peut favoriser ou non l’entrée dans l’algèbre et non évaluer des supposés acquis.

Tableau 3

Les types de tâches présents dans l’évaluation diagnostique

5.2.2 Analyse a priori de la première tâche

L’analyse a priori de la tâche 1 vise à étudier la nature des techniques mobilisées par les élèves et la nature des écritures produites pour déterminer si les élèves généralisent analytiquement ou non et si dans leurs écritures ils mobilisent les caractères procédural et/ou structural. Cette tâche relève d’un problème de généralisation dont le modèle mathématique est une suite arithmétique. Elle consiste à déterminer le nombre d’éléments d’un motif à une étape donnée. L’élève doit repérer la structure du motif à partir des trois premières itérations. Soulignons le choix de l’initialisation du motif. Il conduit à une formulation complexe puisque le terme général de rang n s’exprime en fonction de n-1, ce qui peut s’avérer être une difficulté pour les élèves.

Plusieurs techniques sont possibles, elles sont présentées dans le tableau 4. Nous les hiérarchisons par rapport aux éléments technologico-théoriques qu’elles mobilisent, du comptage à l’algébrique.

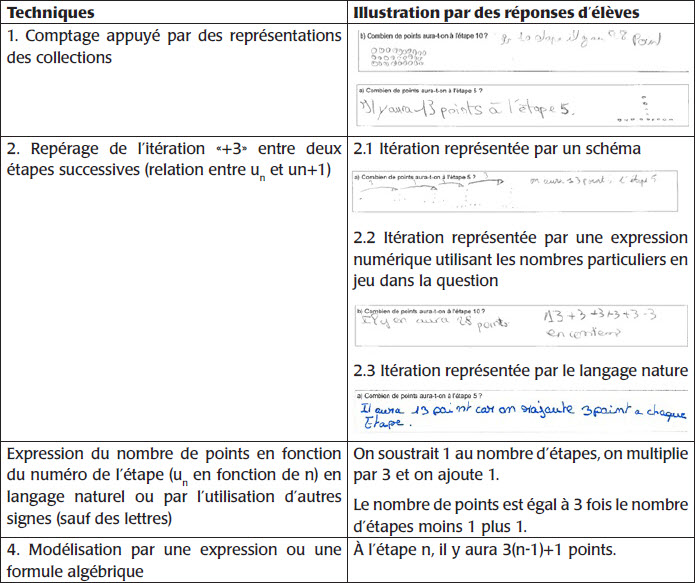
Tableau 4

Techniques et illustrations par des productions d’élèves pour la tâche 1

La technique 1 repose sur du comptage et ne met en jeu ni un raisonnement arithmétique ni un raisonnement algébrique. D’après Radford (2014), seules les techniques 3 et 4 relèvent de l’analycité. La technique 2 consiste à repérer l’itération «+3» et met en jeu une généralisation arithmétique, mais non algébrique, car aucun raisonnement analytique n’est impliqué (Radford, 2014). En effet, elle ne permet pas d’exprimer une généralité sur le nombre de points à une étape donnée en fonction de cette étape. Nous indiquons dans le tableau plusieurs représentations possibles dans des registres différents.

La généralisation ayant peu, voire pas été rencontrée préalablement à la 5^e et n’étant pas demandée ici, nous nous attendions à trouver principalement les techniques 1 et 2.

5.3 Analyse a posteriori de l’évaluation à l’entrée en 5^e

Au total, 129 élèves de 5^e provenant de cinq classes d’un même établissement en Seine Saint-Denis ont passé l’évaluation en septembre 2011. Pour chaque réponse, nous analysons la validité, la technique utilisée et les éléments technologico-théoriques mis en oeuvre.

5.3.1 Analyse a posteriori de tâche 1: Généraliser un motif

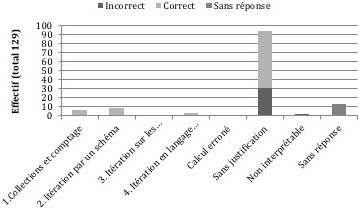
Figure 3

Techniques utilisées par les élèves de la tâche 1.a

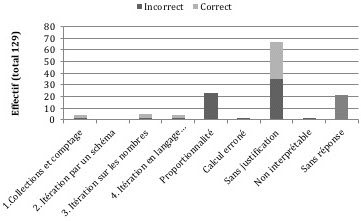
Figure 4

Techniques utilisées par les élèves de la tâche 1.b

73 % des élèves à la question 1.a et 67 % à la question 1.b, (cf. figures 3 et 4) donnent une réponse non justifiée qui conduit dans au moins la moitié des cas à une réponse correcte. Aussi, les productions des élèves donnent peu d’information sur les techniques qu’ils utilisent. Six élèves représentent les collections pour dénombrer le nombre d’éléments. Quelques élèves (10 % à la tâche 1.a et 8 % à la tâche 1.b) justifient leur réponse en exprimant l’itération «+ 3» d’une étape à une autre par un schéma, en utilisant les nombres en jeu ou en langage naturel. Même si, comme souligné précédemment, ces élèves ne sont pas dans un raisonnement analytique, dans certaines productions, dont un exemple est présenté en figure 5, nous pouvons faire l’hypothèse qu’ils utilisent les nombres en jeu pour exprimer l’itération avec une certaine généricité, qui pourra être un levier pour les amener à l’algèbre.

Figure 5

Une généralisation émergente?

Comme attendu, aucune production ne propose de généralisation algébrique du processus, même en langage naturel.

Une technique est apparue à la question 1.b pour près de 18% des élèves (cf. figure 6): elle utilise un raisonnement erroné de proportionnalité que nous n’avions pas anticipé. Ayant repéré le facteur multiplicatif 2 entre les étapes 5 (question 1.a) et 10 (question 1.b), les élèves ont multiplié le nombre de points de l’étape 5 par 2 pour trouver celui de l’étape 10.

Figure 6

Un exemple de raisonnement erroné de proportionnalité

Le pourcentage de non-réponse, qui varie entre 9 % et 20 % sur l’ensemble des tâches de l’évaluation, est difficilement interprétable. Le contexte inhabituel d’une évaluation diagnostique pour les élèves comme pour les enseignants l’a peut-être favorisé.

5.3.2 Analyse a posteriori de la tâche 2: Écrire une formule pour calculer le périmètre d’un carré

Plusieurs formulations sont envisageables pour calculer le périmètre d’un carré: une expression ou une formule, avec des nombres, avec des mots ou des lettres, prenant en compte la mesure ou non.

Figure 7

Les différentes réponses des élèves à la tâche 2

54 % des élèves mobilisent des lettres ou des mots pour exprimer une relation entre deux grandeurs (cf. figure 7). Parmi eux, 69 % redonnent une expression ou une formule du périmètre du carré faisant usage des lettres, dont la moitié est correcte. 31 % redonnent une expression ou formule, mais en utilisant des mots. 19 % utilisent un exemple numérique. Finalement, 6 % ne comprennent pas l’énoncé et 20 % ne répondent pas.

La moitié des élèves fournit donc une réponse ayant un caractère général pour représenter des relations correctes vis-à-vis de la grandeur recherchée. C’est un point d’appui pour l’entrée dans l’algèbre. Les productions informent également de la prégnance du signe d’égalité comme annonce du résultat. Certains élèves (figure 8) mettent un signe d’égalité après l’expression, comme dans l’attente d’un calcul (cm de côté x 4=…)

Figure 8

Quelques productions d’élèves à la tâche 2

5.3.3 Analyse a posteriori de la tâche 3: Calculer le périmètre d’une figure donnée

L’analyse des solutions s’appuie sur l’interprétation de la figure (correcte ou non) et de la grandeur en jeu et sur le type d’écriture utilisé dans le calcul du périmètre (posé en colonne), exprimant le processus de calcul (calcul pas à pas) ou le résultat (calcul en ligne).

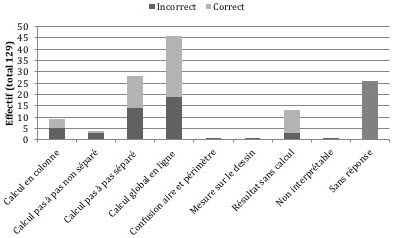
Figure 9

Écritures utilisées par les élèves dans la tâche 3

Figure 10

Utilisation ou non de la multiplication comme addition itérée

Figure 11

Quelques exemples de productions d’élèves sur la tâche 3

Les productions (cf. figures 9 et 11) montrent une forte diversité des écritures utilisées par les élèves: 6 % des élèves écrivent leurs calculs en colonne, 22 % écrivent leurs calculs pas à pas, 3 % les écrivent en pas-à-pas non séparé et 16 % des élèves qui écrivent un calcul en ligne utilisent l’addition itérée et non la multiplication (cf. figure 10). Ces productions donnent à voir certaines habitudes d’écriture des calculs héritées de l’école primaire. Mais ces habitudes présentent des limites. Elles ne permettent pas de rendre compte de l’ensemble des calculs avec une même expression et, par conséquent, elles privilégient l’aspect procédural des expressions numériques. Les élèves qui écrivent des calculs non séparés favorisent majoritairement le statut d’annonce du résultat du signe d’égalité et ne cherchent pas à conserver la dénotation des expressions, ce qui pourra être un frein lorsqu’ils seront confrontés à des transformations d’expressions algébriques ou d’équations. De plus, nous soulignons que 45 % des réponses sont erronées, souvent en raison de la présence de nombres décimaux.

L’évaluation diagnostique a donc permis de décrire des aspects du rapport personnel à l’arithmétique construit en début de collège qui peuvent s’ériger en obstacle pour l’entrée dans l’algèbre. À travers les analyses menées, il ressort que les principaux indicateurs favorisant l’entrée dans l’algèbre sont peu présents et doivent être travaillés avec les élèves.

6. Discussion et conclusion

Dans le cadre de cet article, nous avons défini des critères pour analyser l’activité arithmétique avant l’entrée dans l’algèbre (cf. section3). En nous plaçant dans le cadre de la théorie anthropologique du didactique, nous avons listé des types de tâches nécessaires pour travailler ces différents critères. Cette étude reste exploratoire et pourra conduire à établir une praxéologie épistémologique de référence (Bosch et Gascon, 2005) relativement aux savoirs numérico-algébriques (Constantin, 2017). Une telle praxéologie de référence serait un point d’appui pour analyser la complétude des programmes et dégager des praxéologies implicites ou peu travaillées, mais nécessaires à l’entrée dans l’algèbre.

L’évaluation proposée ne couvre qu’une partie des types de tâches définis dans la section 4.2 et ne permet d’analyser que partiellement le rapport personnel à l’arithmétique avant l’entrée dans l’algèbre. Il s’agissait d’une première version, qui a néanmoins permis aux enseignants de l’équipe de prendre conscience de la nécessité d’enrichir les aspects épistémologiques d’objets mathématiques que sont l’égalité, les opérations, les expressions numériques, ainsi que des propriétés de ces objets, souvent déjà rencontrées en arithmétique (cf. section 3) comme la distributivité. Ces aspects épistémologiques sont des leviers pour construire des stratégies d’enseignement adaptées aux besoins d’apprentissage des élèves (Cusi et Malara, 2012).

Notre étude met en lumière la nécessité d’inscrire dans les manuels de primaire des types de tâches actuellement peu présents, comme du calcul réfléchi pour produire et interpréter des écritures équivalentes d’un même nombre, ou de la production d’expressions numériques en résolution de problèmes, notamment de généralisation.

Dans la résolution de problèmes arithmétiques à plusieurs opérations mettant en jeu des programmes de calcul (Ruiz-Munzón et al., 2012), il est également possible d’encourager les élèves à produire des écritures en ligne de leurs calculs et non uniquement des écritures pas à pas. L’usage du signe d’égalité et des opérations en accord avec celui qui sera fait en algèbre, et du caractère structural des expressions serait alors favorisé. De plus, produire une expression numérique en ligne pour résoudre un problème arithmétique permet de modéliser la situation puisqu’elle donne les relations entre les objets (Butlen et Pézard, 2000).

Notes

• [1] Pour plus d’informations, voir http://ife.ens-lyon.fr/lea/le-reseau/les-differents-lea/college-martin-du-gard.
• [2] Les praxéologies sont définies à partir de l’étude des programmes, des documents d’application et des principaux manuels utilisés dans les classes.