Résumés
Résumé
Différentes recherches indiquent que les élèves présentent des difficultés à résoudre des problèmes algébriques. D’autres montrent qu’ils peuvent résoudre ce type de problèmes avant que l’algèbre soit enseignée. Cet article analyse ce que font les élèves avant et après l’enseignement de l’algèbre à l’école. Nous avons analysé la production de 528 élèves (6e année à secondaire 2 au Québec, élèves de 11 à 14 ans). Les résultats indiquent que les procédures privilégiées lors de la résolution de problèmes algébriques sont semblables avant et après son enseignement. Nous observons deux catégories de difficultés: la compréhension de relations du problème et la manipulation d’équations algébriques. Identifier et discuter ces difficultés permet de mieux cibler des éléments de réflexion à considérer pour travailler les problèmes en classe et pour favoriser le passage de la résolution de problèmes écrits en mots vers l’écriture des expressions algébriques.
Mots-clés :
- apprentissage de l’algèbre,
- enseignement primaire-secondaire,
- difficultés en algèbre,
- problèmes de partage inéquitable,
- résolution de problèmes mathématiques
Abstract
Some studies indicate that students struggle with solving algebra problems. Others show that they are able to solve such problems before they are taught algebra. This article examines what students do prior and subsequent to their school-based algebra instruction. We examined the productions of 528 students (6th year of primary school to 2nd year of secondary school in Quebec, students 11–14 years old). The results indicate that the procedures used to solve algebra problems are similar before and after students receive algebra instruction. Two categories of difficulties emerge: understanding problem relationships and manipulating algebraic equations. Identifying and discussing these difficulties offers a way to better determine elements of reflection to take into account in order to work on problems in class and to promote the shift from solving problems trough words to writing algebraic expressions.
Keywords:
- algebra learning,
- primary-secondary instruction,
- difficulties in algebra,
- unfair division problems,
- mathematical problem-solvingant
Resumen
Diversas investigaciones indican que los estudiantes presentan dificultades en la resolución de problemas algebraicos. Otras muestran que ellos pueden resolver este tipo de problemas antes de su enseñanza. Este artículo analiza lo que los alumnos hacen antes y después de la enseñanza del álgebra en la escuela. Hemos analizado la producción 528 estudiantes (desde sexto año de primaria hasta segundo año de secundaria en Quebec, cuyas edades fluctúan entre los 11 y los 14 años). Los resultados indican que los procedimientos privilegiados en la resolución de problemas algebraicos son similares antes y después de la enseñanza del álgebra. Observamos dos categorías de dificultades: por una parte, la comprensión de las relaciones en el problema y por otra, la manipulación de las ecuaciones. Identificar y discutir sobre esas dificultades permite enfocar mejor los elementos de reflexión que deben considerarse para trabajar con problemas en clase y para favorecer la transferencia de problemas descritos en palabras hacia la escritura de expresiones algebraicas.
Palabras clave:
- aprendizaje del álgebra,
- enseñanza primaria y secundaria,
- dificultades en álgebra,
- problemas de repartición inequitativa,
- resolución de problemas matemáticos
Corps de l’article
1. Introduction
Différentes recherches portant sur l'apprentissage de l'algèbre indiquent que les élèves présentent des difficultés à résoudre des problèmes de ce type (Adihou et al., 2015; Bednarz et Janvier, 1996; Chevallard, 1989; Da Rocha Falcão, 1996; Demonty, Fagnant, et Vlassis, 2015; Duval, 2000; Kieran, 1992; Lochhead et Mestre, 1988; Marchand et Bednarz, 2000). D'autres études montrent également que les élèves sont en mesure de résoudre différents types de problèmes algébriques avant tout enseignement de l'algèbre (Adihou et al., 2015; Bronner, 2015; Câmara dos Santos et Oliveira, 2010; Oliveira et Rhéaume, 2014; Smith et Thompson, 2008). En tant que chercheures, nous nous questionnons à savoir si les habiletés des élèves et les difficultés rencontrées pour résoudre des problèmes algébriques sont les mêmes avant et après l’apprentissage de l'algèbre à l’école.
Par ailleurs, depuis les études fondamentales sur l'apprentissage de l'algèbre dans les années 1990-2000 (Bednarz et Janvier, 1996; Kieran, 1991; Marchand et Bednarz, 2000; Radford et Grenier, 1996; Radford, 1996), une nouvelle vague de recherches s'intéresse à cet apprentissage. Ces nouvelles études sont motivées, entre autres, par différentes réformes et programmes d'études qui ont été depuis mis en place. Ces programmes préconisent une compréhension chez l’élève basée sur la recherche de sens et le développement d'une pensée algébrique dès le début du primaire afin de faciliter le passage vers des mathématiques plus formelles. Par exemple, le programme du Brésil indique qu'au primaire certaines dimensions touchant le travail algébrique doivent être abordées (les régularités, la généralisation et les propriétés de l'égalité) sans avoir recours à l'utilisation des lettres. Tandis qu'au secondaire, les élèves seront amenés à comprendre les différents sens des variables numériques et à établir la généralisation d'une propriété, entre autres (Ministério da educação, 2017). Quelques études récentes s'intéressent plus particulièrement à l'apprentissage précoce de l'algèbre (Early Algebraization) (Cai et Knuth, 2011a; Kaput, Carraher, et Blanton, 2008) comme moyen de développer la pensée algébrique au primaire et, par conséquent, de faciliter l'apprentissage de l'algèbre à l'école secondaire. De notre côté, cette nouvelle vague nous amène plutôt à investiguer le développement de la pensée algébrique par la résolution de problèmes dans le contexte québécois où l’introduction de l'algèbre a lieu au début du secondaire (13-14 ans). Ceci permet d'identifier les difficultés et les habiletés à résoudre des problèmes en algèbre avant et pendant son introduction au secondaire auprès des élèves de la fin du primaire (6e année) et du début du secondaire (secondaires 1 et 2).
2. Enjeux liés à l'apprentissage de l'algèbre
À ce jour, différentes recherches ont fait ressortir des enjeux liés à l'apprentissage de l'algèbre. Quelques chercheurs ont étudié les difficultés d'un point de vue épistémologique (Artigue, 2012; Chevallard, 1989; Kieran, 1992). Ils ont mis en évidence l'existence d'une certaine rupture entre les raisonnements arithmétique et algébrique qui peut se traduire par la non-compréhension du sens de l'égalité ou encore une non-reconnaissance de la structure algébrique et qui fait en sorte que les élèves manipulent les relations par des procédures arithmétiques souvent familières, mais pas toujours appropriées à la résolution des situations proposées. Ceci étant dit, plusieurs élèves sont aussi en mesure de résoudre ce type de problème au moyen de procédures arithmétiques correctes.
Il est important de situer le raisonnement algébrique et la procédure algébrique pour contextualiser cette étude. Bednarz et Charbonneau (1992) caractérisent le raisonnement algébrique d'après le type d'engagement dans le problème, la distance prise lors du traitement des grandeurs et des contextes, la considération de certaines règles générales de manipulation qui guident la résolution, la désémantisation du langage, le type de réflexion sur le nombre et les opérations et le caractère analytique du raisonnement et de la recherche d'un procédé général. La mise en place de tous ces éléments caractérise la procédure algébrique.
2.1 Différentes procédures possibles
Certaines études ont répertorié des procédures mises en place lors de la résolution des problèmes algébriques (Bednarz, Janvier, Mary, et Lepage, 1992; Câmara dos Santos et Oliveira, 2010; Oliveira et Câmara dos Santos, 2011). Par ailleurs, les résultats d'une étude antérieure (Oliveira et Rhéaume, 2014) amènent un autre élément à considérer lors de l'étude des procédures identifiées. Ce que nous entendons par «explicitation des relations», ce sont les traces laissées par l'élève qui indiquent de quelle manière ces relations sont mobilisées. L’élève prend des notes ou retranscrit les relations, symbolise et dessine des flèches afin de représenter explicitement les relations. Ensuite, cette explicitation écrite est utilisée pour la construction des équations ou pour faire les calculs. Chaque procédure mobilisée par les élèves pour résoudre des problèmes de partage inéquitable est expliquée ci-dessous[1].
-
Fait une division: L’élève divise le total connu par le nombre de sujets/objets présents dans l’énoncé du problème et attribue le résultat de cette division à l’un des sujets/objets ou parfois à tous les sujets/objets. Le résultat de cette division n'est nullement réinvesti dans l'établissement des relations présentes dans le problème. De notre point de vue, cette procédure mène nécessairement à une réponse erronée.
-
Partage équitable: L’élève partage en parts égales la quantité totale donnée dans le problème par le nombre de sujets/objets qui la compose. Ensuite, il utilise cette «moyenne» comme point de départ pour appliquer les relations indiquées dans le problème et ainsi obtenir le nombre pour chaque sujet/objet.
-
Essai numérique: L’élève attribue un nombre de départ aux sujets/objets (pour l’une des valeurs recherchées), un certain état à partir duquel le total va pouvoir être reconstruit une relation à la fois. Nous distinguons deux types d’essais. Cette distinction précise la manière d’aborder le problème:
-
Sans explicitation des relations (SER): Ce type d'essai illustre un travail qui se centre d’abord sur des nombres. L’élève ne représente pas explicitement les relations entre ces nombres.
-
Avec explicitation des relations (AER): Ce type d'essai illustre un travail qui se centre d’abord sur l’explicitation des relations entre les sujets/objets pour ensuite entamer un travail sur ces nombres. Après quoi, l’élève essaie de trouver les nombres qui respectent ces relations.
-
-
Total comme source: En partant du total indiqué dans l’énoncé, l’élève applique les relations établies dans le problème pour trouver les nombres. Le travail sur les relations sert à contrôler les grandeurs en jeu et fait référence à un raisonnement en termes de parts. Nous distinguons deux types de procédures «total comme source» qui se différencient par la manière d’aborder le problème:
-
État final (EF): L’élève se construit dès le départ, avant même de commencer les opérations, une représentation globale des relations présentes dans le problème. Ensuite, il identifie l’état final et l’utilise lorsqu’il opère sur le total (la source).
-
États intermédiaires (EI): À partir du total (la source), l’élève identifie et applique les relations une à la fois et étape par étape (états intermédiaires).
-
-
Algébrique: L’élève met en oeuvre de manière conjointe un certain nombre d’actions. D’abord, avant même de commencer les opérations, il se construit une représentation globale des relations présentes dans le problème. Ensuite, il dégage des structures algébriques et manipule ces expressions algébriques par le biais d’une notation symbolique.
-
Calcul quelconque: L’élève fait un calcul en utilisant un ou des nombres qui apparaissent dans l’énoncé du problème. Ce calcul n’est nullement lié aux relations dans le problème.
-
Non identifiée: L’élève n’écrit que la réponse ou nous ne sommes pas en mesure de reconnaître la procédure utilisée.
2.2 Identifier et construire l'expression algébrique
Un autre enjeu porte sur le fait que les élèves ne sont pas toujours en mesure d'identifier ou de construire l'expression algébrique associée à un problème présenté sous la forme d'un énoncé écrit (Demonty et al., 2015; Kaput et Sims-Kinght, 1983; Lochhead et Mestre, 1988; Oliveira et Rhéaume, 2014). Pour surmonter cette difficulté, Kaput et Sims-Kinght (1983) insistent sur l'importance de favoriser l'usage de mathématiques de plus en plus formelles afin de développer des habiletés à traduire à partir de différents systèmes de représentation. Leurs propos rappellent la distinction à faire entre la capacité de mettre en jeu un raisonnement mathématique approprié et l’habileté à construire des expressions traduisant les mêmes raisonnements mathématiques. Ces habiletés sont étroitement liées à d'autres systèmes de représentation, dont le langage.
Le besoin de développer les habiletés liées à la traduction nous rappelle la difficulté liée au passage d'un mode de représentation à un autre. Ainsi, une des conséquences de cette difficulté serait que les élèves ne sont pas en mesure de dégager les relations. Une autre conséquence serait qu'ils ne verraient pas ou perdraient de vue l’enchaînement des relations du problème. Cette difficulté rejoint les résultats des travaux d'autres chercheurs (Bednarz et Janvier, 1996; Booth, 1984, 1988; Hitt, 2004; Kieran, 1992) où la traduction des données présentées en langage naturel s'avère être une tâche très ardue pour les élèves.
2.3 Différentes difficultés possibles
D’autres recherches (Artigue, 2012; Bednarz et Janvier, 1994; Cai et Knuth, 2011a, 2011b; Kieran, 1991, 1992, 2007; Marchand et Bednarz, 1999) suggèrent qu'il faut davantage faire travailler les élèves sur la compréhension de la structure du problème. Comme le soulignent Cai et Knuth (2011b), l'apprentissage de l'algèbre se doit d’aller au-delà de l’efficacité avec les opérations arithmétiques vers une explicitation des structures sous-jacentes. Ces pistes rejoignent les résultats concernant les difficultés identifiées chez les élèves.
La revue de littérature (Booth, 1984; Demonty et al., 2015; Kaput et Sims-Kinght, 1983; Lochhead et Mestre, 1988; Vlassis et Demonty, 2000; Vlassis, Fagnant et Demonty, 2015) a permis d’identifier plusieurs difficultés pouvant influencer la résolution d'un problème algébrique. Ces difficultés sont associées à différents moments de la résolution. Chaque difficulté est expliquée dans le tableau 1.
Tableau 1
Liste de difficultés identifiées
L’étude des habiletés et des difficultés lors de la résolution de problèmes algébriques s’avère féconde pour identifier et clarifier les enjeux vécus par les élèves lors des premiers apprentissages de l'algèbre. La résolution de problèmes fait appel à la mise en place des relations et offre une certaine latitude aux élèves quant aux choix des procédures.
3. Recueil et analyse de données
3.1 Recueil de données
Afin de documenter les procédures mobilisées par les élèves avant et après l’introduction de l’algèbre ainsi que les difficultés qu’ils peuvent rencontrer, nous avons proposé à des élèves de résoudre individuellement six problèmes de partage inéquitable. Au total, 352 élèves, dont 61 de 6e année (11-12 ans), 140 de 1re secondaire (12-13 ans) et 151 de 2e secondaire (13-14 ans), ont participé à l’étude. Ces élèves proviennent de huit écoles (une école privée et sept écoles publiques) de la région de Québec. Toutes les écoles participantes sont situées dans des milieux socioéconomiques similaires. Cette recherche descriptive est l’occasion de porter une attention particulière au travail des élèves en termes de procédures mobilisées et de difficultés rencontrées.
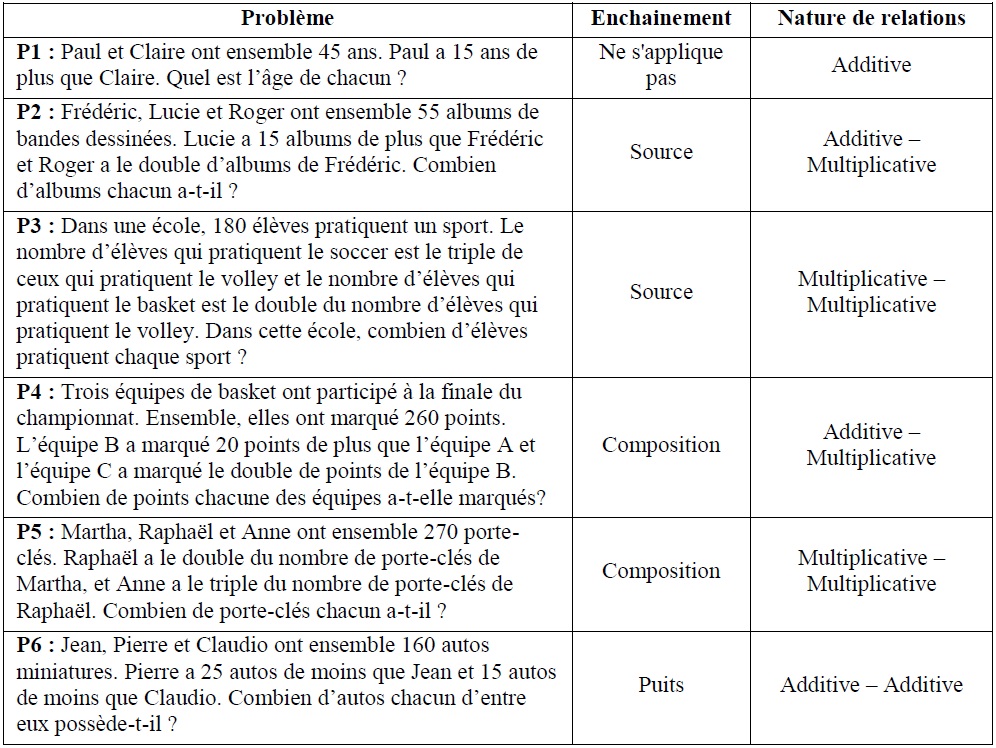
3.2 Différents types de problèmes
Les six problèmes proposés dans ce questionnaire sont inspirés des problèmes déjà étudiés dans d'autres recherches portant sur le partage inéquitable (Bednarz et Janvier, 1994, 1996; Câmara dos Santos et Oliveira, 2010; Marchand et Bednarz, 1999, 2000; Oliveira et Câmara dos Santos, 2011).
Pour favoriser l’engagement des élèves dans cette activité, le premier problème présente seulement une relation. Comme il ne comporte qu’une seule relation, ce problème ne sera pas analysé. Les autres problèmes comportent tous deux relations et sont présentés de manière aléatoire dans le questionnaire.
Tableau 2
Structure de problèmes donnés aux élèves
3.3 Analyse des données
Les productions des élèves ont fait d’abord l’objet d’analyses quantitatives: celle de la variance du taux de réussite et celle des procédures mobilisées. Ensuite, nous avons examiné les procédures mises en place ainsi que les difficultés rencontrées par les élèves par le biais d’une analyse qualitative. Les catégorisations ont été réalisées en fonction des procédures et des difficultés déjà répertoriées précédemment dans cet article.
4. Résultats
Afin de situer les élèves, nous présentons d'abord le taux de réussite par problème. Ces résultats permettent d'établir des distinctions entre les trois niveaux scolaires puis d'identifier les problèmes que les élèves réussissent mieux à chacun des niveaux. Ensuite, nous présentons les procédures privilégiées pour l'ensemble des élèves et les principales difficultés dégagées.
4.1 Le taux de réussite
La figure 1 permet d’observer le taux de réussite chez les élèves pour chacun des problèmes.
Figure 1
Taux de réussite des élèves ayant répondu les problèmes 2 à 6 selon le niveau scolaire
D’une part, il n'est pas surprenant d’observer que les élèves du secondaire réussissent mieux que les élèves du primaire, et ce, pour chaque problème. Puisque le taux de réussite augmente du primaire au secondaire, le niveau scolaire semble jouer un rôle dans la réussite des problèmes de partage inéquitable. Néanmoins, il y a une différence significative entre le taux de réussite des élèves de 6e année et des élèves de secondaire 2 seulement pour les problèmes 3 (z = -2.4421 et p = 0.014) et 4 (z = -3.4756 et p = 0.000). Une différence significative pour seulement deux des cinq problèmes atténue l'écart entre ces deux niveaux scolaires. Nous pouvons même affirmer que la figure 1 illustre une progression attendue en ce qui concerne l'apprentissage de l'arithmétique due à l'expérience, l'âge et la scolarisation. Nous observons avec surprise que les taux de réussite des élèves de secondaire 1 et 2 sont très proches pour tous les problèmes et qu’il n'y a aucune différence significative entre ces deux niveaux. Étant donné que l’introduction explicite aux différentes notions de l’algèbre a commencé pour les élèves de 2e secondaire, on aurait pu s'attendre à un taux de réussite significativement plus élevé chez ces derniers.
D'autre part, ces résultats illustrent que le problème 2 et le problème 3 sont les plus faciles à résoudre pour l’ensemble des élèves. Par niveau scolaire, il n’y a aucune différence significative entre ces deux problèmes. L’analyse des taux de réussite entre les différents problèmes nous permet d’observer une différence significative entre le problème 2, ayant le plus haut taux de réussite, et les problèmes 4 et 6, ayant les plus bas taux de réussite, et ce, pour chaque niveau scolaire (p < 0.05). En accord avec Marchand et Bednarz (1999), les problèmes de type source (problème 2 et 3) présentent un enchaînement moins complexe à résoudre que les problèmes de type combinaison ou puits (problème 4, 5 et 6). Le type d'enchaînement dans la structure algébrique des problèmes semble donc également jouer un rôle dans la réussite de ces problèmes.
Les résultats illustrent que plusieurs élèves présentent des habiletés arithmétiques nécessaires à la résolution des problèmes de partage inéquitable avant l’introduction à l’algèbre. Ils pointent aussi le rôle que peuvent jouer, sur la réussite du problème, les variables imbriquées dans une structure algébrique de partage inéquitable. Par exemple, nous remarquons la complexité de l'enchaînement «puits» comme source de difficultés au problème 6. Nous remarquons aussi que lorsque des problèmes présentent un type d'enchaînement ayant deux relations de même nature (problèmes 3 et 5, multiplicative/multiplicative) ils sont généralement mieux réussis que ceux présentant des relations mixtes (additive/multiplicative). La mixité dans la nature des relations semble être un autre exemple de complexité qui s’ajoute au type d’enchaînement venant jouer sur le taux de réussite des élèves. Ce constat soulève l'importance de tenir compte de ces variables, de les diversifier, afin d’offrir des situations favorisant un travail sur des relations de natures différentes. Néanmoins, les résultats apportent d'autres questions en ce qui concerne le rôle de l'enchaînement et la nature des relations. Si nous comparons uniquement les problèmes 4 et 6 par niveau scolaire, nous remarquons que le problème 6 a un taux de réussite plus élevé que le problème 4 chez les élèves du primaire et qu'au contraire le problème 4 a un taux de réussite plus élevé que le problème 6 chez les élèves du secondaire. Il est important d'indiquer que le problème 6 est plus complexe que le problème 4. En effet, pour résoudre le problème 6, l’élève doit inverser les relations telles qu’elles sont présentées dans l'énoncé afin de construire l'équation. Dans l'énoncé, on peut lire par exemple «Pierre a 25 autos de moins que Jean». Pour résoudre le problème, l'élève doit voir cette relation comme étant: «le nombre d’autos de Pierre est égal au nombre d’autos de Jean plus 25». Tandis que dans le problème 4 les relations restent les mêmes. Par exemple, nous pouvons lire dans l'énoncé: «L’équipe B a marqué 20 points de plus que l’équipe A». Pour résoudre le problème, l’élève doit voir cette relation comme étant: «Le nombre de points de l’équipe B est égal au nombre de points de l’équipe A plus 20». La relation reste alors semblable.
4.2 Les procédures privilégiées
La figure 2 permet d’analyser l’utilisation de chaque procédure en fonction du problème présenté aux élèves.
Figure 2
Procédures privilégiées par problème pour les élèves de 6e année et de 1er et 2e secondaire ayant répondu à la question
Notons que le nombre d’élèves ayant répondu à la question diffère pour chaque problème, car nous avons pris soin de supprimer de l’analyse les élèves n’ayant pas réalisé le problème.
4.2.1 Essai numérique
L’essai numérique sans explication des relations (SER) est la procédure la plus utilisée par les élèves pour chaque problème. Plus le type de problème est complexe (composition ou puits), plus les élèves ont tendance à se tourner vers cette procédure: 32,74 % pour le problème 4 et 6. Selon ces résultats, il semble que la complexité de la structure du problème ait une influence sur la procédure privilégiée par les élèves. L'analyse du taux de réussite de cette procédure indique qu’elle mène généralement les élèves à la bonne réponse: 76,92 % pour le problème 2, 96,92 % pour le problème 3, 75 % pour le problème 4, 88,75 % pour le problème 5 et 61,96 % pour le problème 6. Même les élèves de secondaire 2 ont eu recours à cette procédure alors qu’ils ont été introduits à l’algèbre et plus précisément à la notation algébrique.
L’autre variante de l’essai numérique, l’essai numérique avec explicitation des relations (AER), est moins utilisée par les élèves (entre 7 % et 12 % en fonction du problème), mais elle les mène également vers la réponse correcte: 76,92 % pour le problème 2, 96,97 % pour le problème 3, 63,89 % pour le problème 4, 82,76 % pour le problème 5 et 82,61 % pour le problème 6.
Dans l’ensemble, la comparaison des résultats de l’essai numérique avec (AER) et sans (SER) explicitation des relations indique que l’explicitation des relations n’assure pas un plus grand taux de réussite chez les élèves, même si l’essai numérique mène majoritairement à une bonne réponse (problème 4 et 5). Nous pouvons envisager que le fait d'expliciter les relations lorsque le problème est plus complexe, comme dans le cas du problème 6, favorise la réussite chez l'élève.
Figure 3
Résolution du problème 5 par essai numérique sans explicitation des relations
Figure 4
Résolution du problème 5 par essai numérique avec explicitation des relations
4.2.2 Non-identifiée
Dans cette catégorie, nous retrouvons les procédures dites «non identifiées», c’est-à-dire que nous ne sommes pas en mesure de reconnaître la procédure utilisée avec certitude ou que l’élève ne mentionne pour réponse qu’un résultat, correct ou non.
Figure 5
Résolution du problème 5 par une procédure non identifiée
Toutefois, étant donné qu’en 2e secondaire un important pourcentage d'élèves se retrouve dans ce cas (37,67 % pour le problème 2, 35,04 % pour le problème 3, 36,36 % pour le problème 4, 33,33 % pour le problème 5 et 38,64 % pour le problème 6), nous avons classé dans le graphique ci-dessous (figure 6) les différentes réponses parmi quatre sous-catégories: les réponses correctes et incorrectes qui indiquent uniquement un résultat (réponse correcte et réponse incorrecte) ainsi que les réponses correctes et incorrectes provenant d’une procédure ne pouvant pas être identifiée avec certitude (non identifiée correcte et incorrecte). Cette analyse permet d’observer que la majorité des réponses indiquent uniquement le résultat (sans procédure illustrée), mais que ce pourcentage diminue en fonction du niveau de difficulté et du taux de réussite des problèmes.
Figure 6
Répartition en pourcentage des procédures non identifiées en secondaire 2 par problème
En effet, nous observons pour le problème 2, qui est un problème bien réussi, que 54,55 % des réponses sont correctes avec uniquement le résultat, tandis que pour le problème 6, qui est plus complexe, nous observons ce type de réponse dans 29,41 %. Face à ces résultats, nous nous posons certaines questions auxquelles nous ne pouvons pas répondre. Ces problèmes sont-ils trop faciles pour un certain pourcentage d’élèves, ce qui faciliterait la mise en place d'un calcul mental? Les élèves ont-ils écrit leurs calculs sur une autre feuille?
4.2.3 Total comme source
Cette procédure se décline en deux variantes distinctes. Tout d’abord, un travail sur l’état final (EF) où l’élève prend en considération l’ensemble des relations présentes dans le problème. À cet effet, la figure 7 illustre un raisonnement en termes de parts attribuées à chacun (x, 2x, 3x) puis une considération des relations entre elles pour établir un total de neuf parts pour l'ensemble des porte-clés. Nous remarquons que cette procédure est surtout utilisée dans la résolution des problèmes 3 (11,84 %) et 5 (8,71 %) (Figure 2). La nature homogène des relations pour ces deux problèmes (multiplicative-multiplicative) semble faciliter une vision d'ensemble des relations. L’autre variante de cette procédure, faisant appel à un certain nombre d’étapes intermédiaires (EI), est davantage utilisée pour la résolution des problèmes 2 (15,57 %) et 6 (12,46 %). L'exemple de la figure 8 illustre les différentes mises en relation exécutées l’une après l’autre. Ainsi, l'élève travaille sur des états intermédiaires.
Figure 7
Résolution du problème 5 par la procédure total comme source état final (EF)
Figure 8
Résolution du problème 3 par la procédure total comme source états intermédiaires (EI)
4.2.4 Algébrique
Puisque la plupart de ces élèves n'ont pas encore appris la notation algébrique à l'école, la procédure algébrique est minoritairement utilisée et n’apparaît qu'en 2e secondaire (2,10 % pour le problème 2, 1,64 % pour le problème 3, 1,42 % pour les problèmes 4 et 6 et 1,52 % pour le problème 5). Toutefois, nous remarquons que cette procédure engendre un taux de réussite variable: 57,14 % pour le problème 2, 80 % pour le problème 3, 25 % pour les problèmes 4 et 5 et 0 % pour le problème 6. Nous pouvons observer une diminution du taux de réussite en fonction de la structure du problème présenté. En effet, ces élèves ne semblent pas être en mesure d’utiliser une procédure algébrique face à un problème plus complexe.
Figure 9
Résolution du problème 5 par la procédure algébrique
4.2.5 Partage équitable
Cette procédure peut mener aussi bien à la réponse erronée qu’à la réponse correcte. Seul le taux de réussite du problème 3 (54,17 %) dépasse les 50 %. En effet, le taux de réussite des autres problèmes s’élève à 33,33 % pour le problème 2, 9,09 % pour le problème 4, 25 % pour le problème 5 et 6,67 % pour le problème 6. Nous remarquons que la structure des problèmes où la nature des relations est multiplicative-multiplicative (problèmes 3 et 5) semble favoriser une réponse correcte, mais cela ne semble pas être le cas lorsqu’il y a des relations additives. La figure 10 illustre ce que fait l'élève lorsqu’il mobilise cette procédure de manière correcte. L'élève partage le tout (270) d’abord de manière équitable pour avoir une idée, une moyenne par personne sur laquelle il s’appuie, pour ensuite être en mesure de jouer avec les nombres et les relations. Finalement, il applique ces relations afin de résoudre le problème.
Figure 10
Résolution du problème 5 par la procédure partage équitable
4.2.6 Division
L’utilisation de cette procédure mène nécessairement à une réponse erronée. L’exemple de la figure 11 illustre une simple division, un partage des porte-clés pour les trois personnes, sans ensuite prendre en considération les relations multiplicatives nécessaires à la résolution du problème. Cette procédure est très peu utilisée par l’ensemble des élèves (4,79 % pour le problème 2, 7,24 % pour le problème 3, 8,19 % pour le problème 4, 6,82 % pour le problème 5 et 3,91 % pour le problème 6). Les pourcentages indiquent qu'elle a été principalement utilisée lors de la résolution du problème 4, problème avec le taux de réussite le plus faible. Une analyse plus poussée de la répartition des procédures par niveau scolaire indique que cette procédure est majoritairement utilisée par les élèves du primaire, et ce, pour chaque problème. Cela pourrait traduire une incompréhension des relations du problème due au niveau scolaire des élèves ou le fait de s’accrocher à une procédure arithmétique plus familière dans le cas des élèves du secondaire.
Figure 11
Résolution du problème 5 par la procédure division
4.2.7 Calcul quelconque
Le fait d'utiliser les nombres présents dans l'énoncé pour faire une opération quelconque démontre le peu de compréhension de l'élève vis-à-vis du problème.
Figure 12
Résolution du problème 5 par la procédure calcul quelconque
D'une façon générale, nous pouvons observer que les élèves tant du primaire que du secondaire participant à notre étude sont en mesure de résoudre plusieurs des problèmes proposés. Leurs résolutions reposent avant tout sur des habiletés arithmétiques. En ce sens, ces élèves privilégient la procédure d'essais numériques comme moyen pour résoudre les différents problèmes. Nous pouvons noter également que même si les élèves de secondaire 2 ont déjà été introduits à l'algèbre et à l'écriture algébrique, ils mobilisent très peu cette procédure pour résoudre les problèmes proposés.
4.3 Les erreurs et les difficultés identifiées
Cette partie porte sur l’analyse des difficultés identifiées parmi les productions des élèves. Dans la mesure du possible, l’analyse sera suivie d’un exemple issu d’une procédure arithmétique (essai numérique, total comme source, division, partage équitable) et d’un exemple issu d’une procédure algébrique.
4.3.1 Identifier et comprendre les relations
Il s’agit d’une des difficultés qu’un élève peut rencontrer lors de la résolution d'un problème. Cette difficulté provient du passage du langage naturel vers une interprétation mathématique. Après la lecture du problème, l’élève ne dégage pas correctement les relations. La procédure de division, où l'élève divise le nombre total selon le nombre de personnages dans le problème, est un exemple de fausse interprétation ou de non-compréhension des relations sous-jacentes en jeu dans le problème.
Dans le premier exemple (figure 14), l’élève utilise une procédure algébrique, mais il ne dégage pas correctement toutes les relations du problème. Il a correctement indiqué que Pierre a 25 de moins que Jean et 15 de moins que Claudio. Comme l'élève a expliciter cette relation, on pourrait croire qu'il a bien compris les relations du problème. Néanmoins, la manière par laquelle il représente Jean et Claudio (les deux sont représentés par l’inconnue x) et par laquelle il construit l'équation nous indique qu’il a copié littéralement l'énoncé du problème et qu’il n’est pas en mesure de faire les transformations pour identifier l’inconnue. La bonne résolution du problème demanderait plutôt la mise en place des relations suivantes pour représenter les quantités de Jean et Claudio.
Figure 13
Présentation de la structure «puits» du problème 5
Nous pouvons observer que toute la résolution du problème est erronée à la suite de cette interprétation des relations.
Figure 14
Exemple algébrique: l'élève ne dégage pas correctement les relations
Une analyse plus approfondie de cette difficulté nous a permis d'observer que certains élèves n’explicitent pas les relations du problème par écrit et parviennent à obtenir la bonne réponse, tandis que d’autres explicitent les relations par écrit et n’obtiennent pas la bonne réponse (figure 15).
Figure 15
Répartition des élèves qui explicitent ou non les relations en fonction de la réussite du problème
Nous notons que la majorité des élèves n’explicite pas les relations et détermine tout de même une réponse correcte: 46,6 % pour le problème 2, 48,6 % pour le problème 4, 33,5 % pour le problème 4, 38,9 % pour le problème 5 et 28,1 % pour le problème 6. Ces pourcentages diminuent lorsqu’il s’agit d’un problème plus complexe (problèmes 4 et 6). Nous observons également que parmi les élèves qui obtiennent une réponse incorrecte les plus nombreux sont ceux qui n’explicitent pas les relations. Nous formulons l’hypothèse que l’explicitation des relations n’est pas un gage de réussite et que la majorité des élèves résolvent les problèmes sans explicitation. Cependant, elle a tout de même une influence sur l’échec de la résolution des problèmes, car le pourcentage de réponses incorrectes est plus faible avec l’explicitation des relations. L’explicitation des relations pourrait favoriser un certain contrôle sur l’interprétation du problème. Ceci étant dit, il faut être prudent lorsqu'on parle d'explicitation des relations en laissant sous-entendre qu'il y a eu compréhension des relations. En effet, l'explicitation pourrait être le fruit d'une transcription directe de l'énoncé sans qu'une réelle compréhension des relations soit en jeu (voir figure 9 et 14). Dans l’ensemble, les données indiquent que la réussite semble davantage reposer sur le fait que l’élève puisse interpréter et dégager correctement les relations plutôt que sur le fait qu’il les explicite, même si cette explicitation semble réduire le taux d’échecs. Si nous examinons à nouveau les figures 9 et 14, nous remarquons que c'est lors de la mise en équation que l'incompréhension des relations se manifeste davantage. Nous pouvons croire que si l'élève les avait effectivement comprises il n'aurait pas accepté le résultat obtenu au moment de retourner aux relations afin d'indiquer la valeur associée à chaque personne (M=135, R=90 et A=45 à la place de M=30, R=60 et A=180). Ce qui nous amène à la difficulté suivante qui touche la mise en équation des relations.
4.3.2 Construire et manipuler l’égalité
Une fois les relations identifiées, certains élèves ne sont pas en mesure de les manipuler dans une équation pour résoudre le problème. À la suite de l’analyse des productions écrites des élèves, nous avons remarqué que ce sont principalement ceux qui mobilisent une procédure algébrique qui rencontrent ce type de difficulté. La difficulté réside dans le fait d’être en mesure de construire une égalité à partir des relations puis de la manipuler pour résoudre le problème.
Dans l’exemple suivant (figure 16), l’élève est capable de dégager correctement les relations du problème. Par contre, il n’est pas en mesure de construire une égalité algébrique qui traduit les relations et il commet des erreurs d’écriture. En effet, lorsqu’il additionne les x+x+x+x, il indique x4 comme réponse. Il ne respecte pas les règles et les conventions d’écriture d’expressions algébriques. De plus, il n’égalise pas la somme au total de 260 points et ne crée donc pas une égalité. L’élève résout de manière arithmétique, une étape à la fois (260-60=200, puis 200 qu’il divise par 4), ce qui indique qu’il ne manipule pas l'égalité dans son ensemble de façon algébrique. Notons aussi que le sens que l'élève attribue au x4 est celui de 4x. Ceci étant dit, cette erreur, dans le cas de ce problème, n'empêche pas l'élève d'obtenir la bonne réponse.
Figure 16
Exemple algébrique: erreur de construction de l'équation
4.3.3 Opérer sur les relations
Certains élèves ne construisent pas d’égalité algébrique ou arithmétique. Ils opèrent par conséquent directement sur les nombres présents dans le problème. Cette façon de faire est identifiée surtout chez les élèves privilégiant une procédure arithmétique (sauf total comme source état final). Dans ce cas-ci, le défi qu'ils rencontrent porte sur l'association des relations identifiées avec des opérations arithmétiques puis sur le fait de les respecter tout au long du processus. Ainsi, lorsque l'élève met en place une procédure arithmétique, il doit garder les relations en tête tout au long du processus de résolution. Ce besoin peut provoquer des erreurs dans la démarche de l'élève, mais les difficultés à garder les relations en tête lors de la mise en place d'une procédure arithmétique ne peuvent pas être considérées comme étant une difficulté associée à l’apprentissage de l’algèbre. Il s'agit plutôt d'une difficulté associée à la procédure privilégiée.
Figure 17
Exemple arithmétique: erreur de calcul ou oubli des relations
Dans l’exemple ci-dessus (figure 17), l’élève n’explicite pas par écrit les relations, mais il les applique correctement à la première ligne de son tableau d’essais numériques (50, 25 et 40). Cependant, lorsqu’il recherche la bonne combinaison de nombres, il perd de vue les relations et commet une erreur à la deuxième ligne (60, 30 et 45) et à la troisième ligne (70, 35, 50).
4.3.4 Retourner aux relations
Une autre difficulté que peut rencontrer un élève, peu importe la procédure mobilisée (algébrique ou arithmétique), est le retour aux relations. Cette difficulté est illustrée, d'abord, dans l’exemple algébrique ci-dessous (figure 17). En effet, l’élève détermine avec précision les relations ainsi que la valeur de x dans l’expression algébrique. Cependant, au moment de contextualiser sa réponse, il n’applique pas correctement les relations et donne une réponse erronée. Lors d’une procédure algébrique, l’élève se dégage des relations le temps de la manipulation. Il doit ensuite contextualiser la solution au moment de formuler la réponse. C'est lors de ce retour que la difficulté peut faire surface.
Figure 18
Exemple algébrique: erreur de retour aux relations
Figure 19
Exemple arithmétique: erreur de retour aux relations
Dans l'exemple ci-dessus (Figure 19), l'élève a identifié les relations au départ. L’explicitation des relations pourrait nous laisser croire que l’élève les comprend. Néanmoins, la suite de ses calculs nous laisse penser que les relations explicitées pourraient être le fruit d'une transcription directe de l'énoncé. Notons que, malgré le fait qu’il y ait une erreur par rapport à la valeur attribuée à Frédéric (20 au lieu de 10), au moment d’identifier les autres valeurs du problème (retourner aux relations), l’élève ne respecte pas les relations qu’il a identifiées au départ.
4.3.5 Lorsque plusieurs difficultés se rencontrent
L’exemple qui suit illustre les multiples défis qu’implique la résolution de problèmes algébriques chez les élèves. À travers les réponses de l’élève (13, 28 et 26) présentées à la figure 19, nous pouvons supposer a priori qu’il voit et applique les relations qui existent entre Frédéric, Roger et Lucie. En effet, dans la reconstruction des résultats dans le tableau, l’élève ajoute bien 15 au nombre d’albums de Frédéric pour obtenir le nombre d’albums de Lucie et a bien doublé le nombre d’albums de Frédéric pour obtenir le nombre d’albums de Roger. Toutefois, une vue d’ensemble de la résolution (d’abord, il soustrait correctement 15 de 55 puis il divise l’état par 3 et non par 4) nous indique qu’il ne traduit pas le problème correctement lors de la construction des égalités qu’il manipule une à la fois (procédure Total comme source EI). Nous ne savons pas s’il perd de vue l’une des relations ou s’il interprète incorrectement le problème au moment d’écrire ce calcul. Autrement dit, il voit les relations au moment où il reconstruit les états, mais n’est pas en mesure de les traduire sous forme d’équation.
Figure 20
Premier exemple de difficultés multiples
Cet exemple présente à la fois la difficulté d’interpréter (÷ 4) ou de maintenir les relations (enchaînement), de traduire cette interprétation en une seule égalité (55-15) ÷ 4 = x, mais aussi de retourner aux relations (ici, le total 55) en fin de résolution. En effet, il en vient à perdre de vue le total puisque 13 + 28 + 26 = 67.
Lorsque nous analysons l'exemple 2 (figure 21), nous remarquons que l'élève présente également différentes difficultés tant pour dégager l’enchaînement des relations (C = x: 2 au lieu de C = 2x + 40) que pour construire et manipuler l'équation ainsi qu'une difficulté associée au retour aux relations.
Figure 21
Deuxième exemple de difficultés multiples
5. Discussion et conclusion
Dans ce qui suit, nous reviendrons sur les trois principaux aspects abordés lors de la présentation des résultats: le taux de réussite des problèmes, les procédures mobilisées et les difficultés rencontrées.
Pour le taux de réussite, les résultats permettent de constater que les élèves réussissent bien les problèmes proposés. Ils sont en mesure d’établir les relations qui sont mises en application parmi différentes procédures (arithmétiques ou algébrique). Néanmoins, certaines structures de problèmes s'avèrent plus complexes et ont une influence sur le type de procédure privilégiée. Il est également important de mentionner le peu de différence qu'il y a entre les élèves du secondaire. Contrairement à ce que l'on pouvait s'attendre les taux de réussite des élèves de secondaire 1 et 2 sont très semblables, et ce, malgré le fait que les derniers ont déjà été introduits formellement aux problèmes de structure algébrique et au contenu d’algèbre (notation, équation, inconnue, égalité). L’autre aspect concernant le taux de réussite porte sur la nature des relations. Celle-ci influence tant le taux de réussite que le type de procédure privilégié par les élèves.
Par rapport aux procédures, nous retenons que lorsque les relations du problème sont de nature multiplicative-multiplicative les élèves présentent une certaine tendance à utilise la procédure «Total comme source» état final. Étant donné que cette procédure fait appel à un raisonnement analytique et se rapproche par certains aspects d'une procédure algébrique (Oliveira et Rhéaume, 2014), il serait intéressant de présenter en classe des problèmes faisant appel à ce type de relations de manière à favoriser un rapprochement entre des procédures arithmétiques initiales des élèves et celle qui sera attendue lors de l'enseignement de l'algèbre.
Ensuite, nous retenons que plus le problème est complexe, plus les élèves privilégient une procédure du type essai numérique. Il est possible que lorsque la structure du problème est plus complexe, les élèves cherchent des procédures avec lesquelles ils se sentent plus confortables. Ainsi, la procédure algébrique étant récente pour eux, ils la laisseraient de côté pour privilégier une procédure qu'ils maîtrisent mieux afin de se centrer sur les relations plus complexes. À cet effet, comme le mentionnent Bednarz et al. (1992), les procédures arithmétiques sont porteuses de sens chez les élèves, mais leur utilisation pour résoudre des problèmes algébriques peut s'avérer ardue, car l’élève doit «garder en tête» toutes les relations, et ce, tout au long du processus de résolution (Oliveira et Rhéaume, 2014). Ceci témoigne du contrôle que les élèves ont sur leur activité mathématique, mais démontre également qu'ils ne font pas encore le passage vers des procédures algébriques et continuent d’utiliser une procédure qui est considérée loin du raisonnement algébrique.
Les difficultés pouvant être rencontrées par les élèves demeurent les mêmes que celles identifiées dans la littérature. Ceci étant dit, cibler «la» difficulté à surmonter s’est avéré une tâche complexe alors que plusieurs scénarios s'entrecroisent. D'abord, il est possible d'identifier différentes difficultés chez différents sujets. Il est également possible d'identifier différentes difficultés chez un même sujet. Ces difficultés émergent à différents moments de la résolution du problème et sont guidées, entre autres, par la structure du problème et par la nature des relations qui sont établies. En ce sens, pour un enseignant, cibler adéquatement en cours d’apprentissage la ou les difficultés pouvant apparaître de manière simultanée lors de la résolution de problèmes peut s'avérer une tâche complexe.
Pour les difficultés liées aux relations présentes dans les problèmes, un résultat qui nous saute aux yeux porte sur l'importance de bien comprendre les relations, de bien les traduire et d’être en mesure de retourner au contexte pour valider et interpréter la réponse numérique obtenue. Ceci n'oblige pas la mise en place d'une procédure algébrique, au contraire. Il est important de considérer aussi que l’explicitation des relations n'est pas garante d’une compréhension du problème. En ce sens, une piste pour le travail de l'enseignant serait de profiter des procédures du type «total comme source» pour faciliter l'entrée dans l'algèbre et réduire les erreurs liées au retour au contexte et aux opérations sur les relations. En effet, à certains moments, les élèves donnent l'impression d'avoir «compris» les relations parce qu’ils l'ont explicitées, mais nous soupçonnons que les traces écrites qui en témoignent ne soient parfois que le résultat d'une transcription directe de l'énoncé du problème. Nous avons aussi pu observer que certaines difficultés n'émergent que lorsque l'élève met en place une procédure algébrique comme celle de «construire et manipuler une égalité».
Finalement, notre questionnement de départ concernait les habiletés et les difficultés des élèves liées à la résolution de problèmes algébriques. L’analyse des productions des élèves nous a amené à cibler davantage l'importance du travail et l’attention portée à l’identification de différents éléments intervenant dans la résolution du problème par l'élève. Parmi ces éléments nous identifions la compréhension des relations, la construction et la manipulation des égalités, l’opération et le retour aux relations. Alors, en tant qu’enseignant, être en mesure de cibler la manifestation de l’ensemble de ces difficultés chez ses élèves est l'une des pistes à considérer lors de l'enseignement. En somme, situer l’élève dans ses apprentissages en algèbre nécessite d’avoir en tête les imbrications possibles entre les connaissances acquises, les difficultés, les structures algébriques impliquées et les procédures privilégiées. La prise en considération de ces imbrications pourrait aider l'enseignant à mieux situer les acquis des élèves, à mieux comprendre les procédures mises en place ainsi qu’à mieux comprendre les erreurs de sources multiples pouvant être présentes dans leurs productions.
Parties annexes
Note
-
[1]
Des exemples des procédures seront présentés dans la section portant sur les résultats.
Bibliographie
- Adihou, A., Squalli, H., Saboya, M., Tremblay, M. et Lapointe, A. (2015). Analyse des raisonnements d’élèves à travers des résolutions de problèmes de comparaison. In Actes du colloque EMF-2015 Pluralités culturelles et universalité des mathématiques: enjeux et perspectives pour leur enseignement et leur apprentissage (p. 1-16). Alger: Université des Sciences et de la Technologie Houari Boumediene.
- Artigue, M. (2012). Enseignement et apprentissage de l’algèbre. Document téléaccessible à l'adresse http://educmath.ens-lyon.fr/Educmath/dossier-manifestations/conference-nationale/contributions/conference-nationale-artigue-1
- Bednarz, N. et Charbonneau, L. (1992). Synthèse des discussions. In Actes du colloque portant sur l’émergence de l’algèbre (p. 111-118). Montréal: CIRADE-UQAM.
- Bednarz, N. et Janvier, B. (1996). Emergence and development of algebra as a problem-solving tool: continuities and discontinuities with arithmetic. In N. Bednarz, C. Kieran et L. Lee (dir.), Approaches to algebra: perspectives for research and teaching (p. 115-136). Dordrecht: Kluwer.
- Bednarz, N. et Janvier, B. (1994). The emergence and development of algebra in a problem solving context: a problem analysis. In Proceedings of the 18th International Conference for the Psychology of Mathematics Education (p. 64-71). Lisbonne: International Group for the Psychology of Mathematics Education.
- Bednarz, N., Janvier, B., Mary, C. et Lepage, A. (1992). L’algèbre comme outil de résolution de problèmes: une réflexion sur les changements nécessaires dans le passage d’un mode de traitement arithmétique à un mode de traitement algébrique. Actes du colloque portant sur l’émergence de l’algèbre (p. 17-31). Montréal: CIRADE-UQAM.
- Booth, L. (1988). Childrens difficulties in beginning algebra. In A. F. Coxford et A. P. Shulte (dir.), The ideas of algebra, K-12 (p. 299-306). Reston: NCTM.
- Booth, L. (1984). Erreurs et incompréhensions en algèbre élémentaire. Petit x, 5, 5-17.
- Bronner, A. (2015). Apport des problèmes de généralisation et d’une analyse praxéologique. In Actes du colloque EMF-2015 Pluralités culturelles et universalité des mathématiques: enjeux et perspectives pour leur enseignement et leur apprentissage (p. 1-18). Alger: Université des Sciences et de la Technologie Houari Boumediene.
- Cai, J. et Knuth, E. (dir.) (2011a). Early Algebraization: a global dialogue from multiple perspectives. Berlin: Springer.
- Cai, J. et Knuth, E. (2011b). Preface to part I. In J. Cai et E. Knuth (dir.), Early Algebraization: a global dialogue from multiple perspectives (p. 3-4). Berlin: Springer.
- Câmara dos Santos, M. et Oliveira, I. (2010). Estratégias e registros utilizados por alunos de 6° ano na resolução de problemas de estrutura algébrica. In Actes du colloque X Encontro Nacional de Educação Matemática (p. 1-11). Salvador, Brésil.
- Chevallard, Y. (1989). Le passage de l’arithmétique à l’algèbre dans l’enseignement des mathématiques au collège – deuxième partie: perspectives curriculaire: la notion de modelisation. Petit x, 19, 43-72.
- Da Rocha Falcão, J. T. (1996). Clinical analysis of difficulties in algebraic problem solving among brasilian students: principal aspects and didactic issues. Proceedings of the 20th International Conference for the Psychology of Mathematics Education (p. 257-264). Seville: Universitat de Valencia .
- Demonty, I., Fagnant, A. Et Vlassis, J. (2015). Différences entre les raisonnements mis en place par les élèves avant et après l’introduction de l’algèbre? Actes du colloque EMF-2015 Pluralités culturelles et universalité des mathématiques: enjeux et perspectives pour leur enseignement et leur apprentissage (p. 1-17). Alger: Université des Sciences et de la Technologie Houari Boumediene.
- Duval, R. (2000). Écriture, raisonnement et découverte de la démonstration en mathématiques. Recherches en didactique des mathématiques, 20(2), 135-170.
- Hitt, F. (2004). Les représentations sémiotiques dans l’apprentissage de concepts mathématiques et leur rôle dans une démarche heuristique. Revue des sciences de l’éducation, 30(2), 329-354.
- Kaput, J. J., Carraher, D. W. et Blanton, M. (dir.) (2008). Algebra in the early grades. New York: Routledge.
- Kaput, J. J. et Sims-Kinght, J. (1983). Errors in translations to algebraic equations: roots and implications. Focus on Learning Problems in Mathematics, 5(3-4), 63-78.
- Kieran, C. (2007). Learning and teaching algebra at the middle school through college levels: Building meaning for symbols and their manipulation. In F. K. Lester Jr (dir.) Second handbook of research on mathematics teaching and learning (p. 707-762). Charlotte: Information Age.
- Kieran, C. (1992). The learning and teaching of school algebra. In D. A. Grouws (dir.), Handbook of research on mathematics teaching and learning (p. 390-419). New York: Macmillan.
- Kieran, C. (1991). Une approche aidante pour faire la transition avec l’algèbre. Bulletin de l’A.P.M.E.P., Mai, 25-28.
- Lochhead, J. et Mestre, J. P. (1988). From words to algebra: Mending misconceptions. In A. F. Coxford et A. P. Shulte (dir.) The ideas of algebra, K-12 (p. 127-135). Reston: NCTM.
- Marchand, P. et Bednarz, N. (2000). Développement de l’algèbre dans un contexte de résolution de problèmes. Bulletin AMQ, 40(4), 15-25.
- Marchand, P. et Bednarz, N. (1999). L’enseignement de l’algèbre au secondaire: une analyse des problèmes présentés aux élèves. Bulletin AMQ, 39(4), 30-42.
- Ministério da educação. (2017). Base nacional comum curricular: educação é a base (3e versão). Brasilia, Brésil.
- Oliveira, I. et Rhéaume, S. (2014). Comment s’y prennent-ils? La résolution de problèmes de partage inéquitable par des élèves avant enseignement formel de l’algèbre. Canadian Journal of Science, Mathematics and Technology Education, 14(4), 404-423.
- Radford, L. (1996). Sur la résolution de problèmes dans la classe de mathématiques. Le Nouvel Ontario, 18, 11-34.
- Radford, L. et Grenier, M. (1996). Entre les choses, les symboles et les idées ... une séquence d’enseignement d’introduction à l’algèbre. Revue des sciences de l’éducation, 22(2), 253-256.
- Smith, J. P. et Thompson, P. W. (2008). Quantitative reasoning and the development of algebraic reasoning. In J. J. Kaput, D. W. Carraher et M. L. Blanton (dir.), Algebra in the early grades (p. 95-132). New York: Routledge.
- Vlassis, J. et Demonty, I. (2000). La résolution des équations du premier degré à une inconnue. Cahiers du Service de Pédagogie Expérimentale de Université de Liège, 3(4), 35-51.
- Vlassis, J., Fagnant, A. et Demonty, I. (2015). Symboliser et conceptualiser, deux facette indissociables de la pensée mathématique: l’exemple de l’algèbre. In Actes du colloque EMF-2015 Pluralités culturelles et universalité des mathématiques: enjeux et perspectives pour leur enseignement et leur apprentissage (p. 1-13). Alger: Université des Sciences et de la Technologie Houari Boumediene.
Liste des figures
Figure 1
Taux de réussite des élèves ayant répondu les problèmes 2 à 6 selon le niveau scolaire
Figure 2
Procédures privilégiées par problème pour les élèves de 6e année et de 1er et 2e secondaire ayant répondu à la question
Figure 3
Résolution du problème 5 par essai numérique sans explicitation des relations
Figure 4
Résolution du problème 5 par essai numérique avec explicitation des relations
Figure 5
Résolution du problème 5 par une procédure non identifiée
Figure 6
Répartition en pourcentage des procédures non identifiées en secondaire 2 par problème
Figure 7
Résolution du problème 5 par la procédure total comme source état final (EF)
Figure 8
Résolution du problème 3 par la procédure total comme source états intermédiaires (EI)
Figure 9
Résolution du problème 5 par la procédure algébrique
Figure 10
Résolution du problème 5 par la procédure partage équitable
Figure 11
Résolution du problème 5 par la procédure division
Figure 12
Résolution du problème 5 par la procédure calcul quelconque
Figure 13
Présentation de la structure «puits» du problème 5
Figure 14
Exemple algébrique: l'élève ne dégage pas correctement les relations
Figure 15
Répartition des élèves qui explicitent ou non les relations en fonction de la réussite du problème
Figure 16
Exemple algébrique: erreur de construction de l'équation
Figure 17
Exemple arithmétique: erreur de calcul ou oubli des relations
Figure 18
Exemple algébrique: erreur de retour aux relations
Figure 19
Exemple arithmétique: erreur de retour aux relations
Figure 20
Premier exemple de difficultés multiples
Figure 21
Deuxième exemple de difficultés multiples
Liste des tableaux
Tableau 1
Liste de difficultés identifiées
Tableau 2
Structure de problèmes donnés aux élèves