Résumés
Résumé
Les besoins en eau, en perpétuelle croissance, nécessitent une mobilisation des eaux de surface. La construction de barrages, menacés par un envasement précoce, nécessite une exploitation rationnelle, moyennant des outils d’aide à la quantification et à la prédiction des dépôts de sédiments. Ainsi, le comblement des retenues peut être simulé pour différentes périodes d’exploitation. La maîtrise du processus transport-déposition des sédiments, constitue un centre d’intérêt vers lequel convergent plusieurs approches : prédiction, modélisation stochastique et modélisations mathématique et physique. De multiples interactions existent entre les matériaux solides formant le lit, ceux transportés à proximité du fond et ceux se trouvant en suspension, se traduisant par divers modes de transport. Cette contribution présente un modèle numérique qui se prête au calcul par ordinateur dont le comportement morphologique du lit d’un cours d’eau peut être facilement simulé. Les étapes de son élaboration sont décrites avec détail, le code de calcul ainsi produit est mis en valeur sur un site test de validation. Un tronçon de 17 km est étudié, entre un barrage en exploitation et une station hydrométrique, sise à l’amont de celui-ci avec une bathymétrie à l’appui. Le transport solide dans le cours d’eau naturel est représenté par un système d’équations unidimensionnelles décrivant un mélange Eau-Sédiment et traduisant les lois de conservation. La méthode utilisée aux différences finies est appliquée, avec un schéma implicite. Elle est du premier ordre en temps et du deuxième ordre en espace. Les équations des écoulements à surface libre, en régime non permanent et graduellement varié, sont utilisées qui, associées à l’équation de continuité solide, forment le système de Saint-Venant-Exner. Une formule de charriage est utilisée pour exprimer le débit solide. Les résultats obtenus expliquent la contribution du transport solide par charriage dans le comblement de la retenue d’un barrage étudié en zone semi-aride.
Mots-clés:
- transport solide,
- charriage,
- modèle numérique,
- Saint-Venant-Exner,
- différences finies,
- barrage SMBA
Abstract
The constant growth of our need for water requires mobilization of surface water. The construction of dams can be envisaged, but many of them are threatened by early sedimentation; there is clearly a need for tools to quantify and forecast sediment deposition. Reservoir sedimentation can be simulated for different operating periods and understanding the process of sediment transport and deposition is a focus of many approaches: prediction, stochastic modeling, mathematical models and physical models have been used. Multiple interactions exist among bed load sediment, sediment transported near the river bed surface, and suspended sediment, resulting in different modes of transport. This contribution presents a numerical model that allows the simulation of the morphologic behaviour of river bed. The stages of its development are described in detail and the resulting computer code is then applied to a validation site. A section of 17 km is studied, between a dam in service and a hydrometric station located upstream of the dam. Sediment transport in the natural stream is presented by a system of one-dimensional equations describing a water-sediment mixture and translating the laws of conservation. The numerical method used is a finite difference method using an implicit scheme. It is first-order in time and second-order in space. Equations for free surface flow, for unsteady and gradually varied conditions, are used. Combined with the sediment continuity equation, these equations form the Saint-Venant-Exner model. The obtained results show the contribution of bed load transport in the sedimentation of the reservoir in a semi-arid zone.
Key words:
- Sediment transport,
- Bed load,
- Numerical model,
- Saint-Venant-Exner model,
- Finite difference,
- Dam SMBA
Corps de l’article
1. Introduction
Les besoins en eau, en croissance perpétuelle, nécessitent la mobilisation des eaux de surface par la construction de barrages dont la capacité se voit menacée par les dépôts de sédiments. Un développement d’outils d’aide à la quantification et la prédiction de ces dépôts est indispensable, se traduisant par la compréhension et la modélisation du transport-déposition des sédiments dans le système barrage-cours d’eau. L’objectif serait d’identifier les dépôts de sédiments sur un tronçon du cours d'eau se jetant dans la cuvette du barrage, dont l’origine provient non seulement de l’érosion hydrique des sols mais aussi du réseau d’écoulement. L’approche unidimensionnelle adoptée convient à ce type de problème, relatif à la continuité sédimentaire sur un tronçon donné, représenté par un profil en long. Ainsi, il est pertinent d’élaborer une approche capable de localiser les zones de dépôt et/ou d’érosion pour des débits liquides donnés qui repose sur l’utilisation des valeurs moyennes, de vitesse, de débit, de pente, etc., pour résoudre un système d’équations unidimensionnelles. Celui-ci décrit un mélange Eau -Sédiment et traduit les lois de conservation valables pour les eaux non profondes qui, associées à l’équation de continuité solide et à une formule empirique de charriage, forment le système de Saint-Venant-Exner.
2. Équations gouvernant le transport solide
Dans un cours d’eau naturel et en présence d’un lit mobile, l’hydraulique fluviale est abordée en étudiant simultanément l’écoulement des phases liquide et solide, par la détermination classique des valeurs moyennes des grandeurs physiques (U,Q,B,H,Z) et d’autres caractéristiques de l’écoulement. Seulement, une bonne caractérisation de la phase solide nécessite l’identification des paramètres mis en équation par les lois dites de conservation, à savoir : la taille des sédiments (courbe granulométrique), la masse volumique des sédiments et la porosité.
2.1 Continuité liquide/solide et équation de quantité de mouvement
La variation de la masse fluide contenue dans un volume donné, pendant un temps donné, est la somme des masses fluides qui y entre, diminuée de celles qui en sortent. Pour la phase liquide, il en résulte l’équation 1 représentant la continuité pour un fluide incompressible dans un canal non prismatique.
où : U, S, h et B représentent la vitesse moyenne, la surface mouillée, le tirant d’eau, la largeur au miroir.
Et pour la phase solide, il en résulte l’équation d’Exner formulée dans l'équation 2, forme finale de l’équation de continuité solide, liant la côte du fond et le débit solide à chaque pas de temps et de l’espace.
où : Z : côte du fond; qs : débit solide par unité de largeur; et P : porosité du fond.
L’équation dynamique exprimant la conservation de la quantité de mouvement pour un écoulement non permanent et non uniforme à ciel ouvert est donnée dans l'équation 3.
avec : g : accélération de la pesanteur; Jf : pente du fond; et Je : pente d’énergie.
Le regroupement des équations différentielles partielles de base 1, 2 et 3 forme le système Saint-Venant-Exner. La pente d’énergie est une relation semi-empirique, donnée par la formule de Chézy pour un écoulement uniforme en régime permanent, équation 4 (Graf et Altinakar, 1993).
où : Je : pente d’énergie; n : représente la rugosité; et RH : le rayon hydraulique.
Ainsi, le système d’équations de Saint-Venant-Exner peut être réécrit pour un canal naturel, équation 5 :
avec : ![]()
Q: débit liquide par unité de largeur.
2.2 Solutions à l’aide des modèles
Selon GRAF et ALTINAKAR (1996), des solutions analytiques aux équations de Saint-Venant-Exner ne sont possibles qu’avec l’utilisation des hypothèses de quasi-stationnarité et de quasi-uniformité de l’écoulement. De ce fait, seule la modélisation numérique peut apporter une solution par couplage ou non des phases solide et liquide, méthode retenue pour le tronçon étudié. Les méthodes implicites aux différences finies couplent les phases liquide et solide par une résolution simultanée qui se prête au calcul par ordinateur. L’algorithme sommaire de simulation expliquant cette démarche est donné à la figure 1.
Figure 1
Algorithme de la modélisation couplée.
Coupled modeling algorithm.
2.3 Approximation aux différences finies des équations de Saint-Venant-Exner
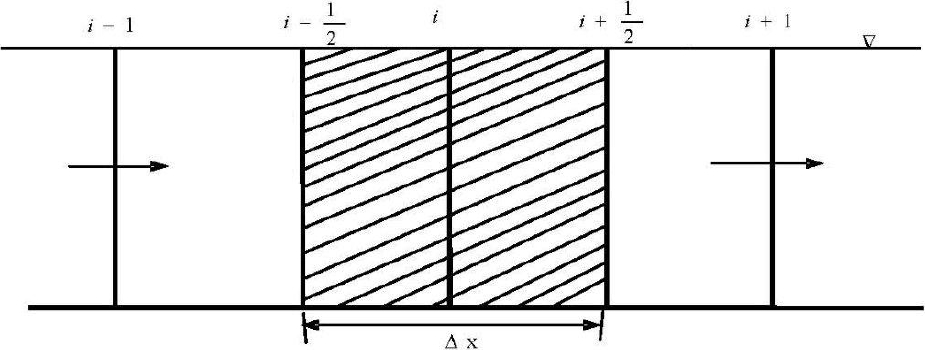
Dans cette discrétisation, l’exposant (j+1) est utilisé pour désigner le temps (t+Δt), quand la variable n’est pas connue explicitement. L’exposant (j) désigne le temps t, quand la valeur de la variable est connue explicitement. L’indice (i) désigne l’abscisse du point concerné, un pas de Δx en avance donne le point d’indice (i+1). La stabilité est un obstacle au calcul numérique, d’où l’utilisation d’un schéma implicite inconditionnellement stable.
2.4 Discrétisation de l’équation de continuité liquide
Pour répondre à la forme implicite, un schéma du premier ordre progressif en temps et centré en espace est choisi, donnant l’équation 6.
avec : i : indice de position pour le volume de contrôle; ![]() : tirant d’eau au temps (t+Δt), et au temps (t); : pas de temps; : pas d’espace entre deux sections adjacentes limitant le volume de contrôle;
: tirant d’eau au temps (t+Δt), et au temps (t); : pas de temps; : pas d’espace entre deux sections adjacentes limitant le volume de contrôle; ![]() : largeur au miroir au point i, et en temps (t);
: largeur au miroir au point i, et en temps (t); ![]() : vitesses d’écoulement au temps (t+Δt) pour les deux sections de contrôle (sections d’entrée et de sortie); et
: vitesses d’écoulement au temps (t+Δt) pour les deux sections de contrôle (sections d’entrée et de sortie); et ![]() : surface d’écoulement limitant le volume de contrôle au temps j (Figure 2).
: surface d’écoulement limitant le volume de contrôle au temps j (Figure 2).
Figure 2
Volume de contrôle pour l’équation de continuité.
Control volume for the liquid-phase continuity equation.
2.5 Discrétisation de l’équation dynamique
Dans l’équation dynamique (équation 3), remplaçons Je par l’expression donnée par l’équation 4 :
La discrétisation se fait avec une attention particulière car l’équation dynamique regroupe les variables des trois principales équations à résoudre. En s’appuyant sur le volume de contrôle (Figure 3), l’approximation des dérivées partielles devient moins difficile.
Figure 3
Volume de contrôle pour l’équation dynamique.
Control volume for the momentum equation.
De la discrétisation de l’équation 1, trois inconnues en temps (t+∆t) et deux inconnues représentant respectivement la vitesse au stade i - 1/2 et i + 1/2 et la hauteur d’écoulement au stade sont obtenues. Celles-ci devant figurer obligatoirement dans la discrétisation de l’équation dynamique 7, conduisant ainsi à une double discrétisation pour la vitesse U au stade i - 1/2 et i + 1/2. Le schéma aux différences finies suivi est progressif en temps et centré en espace. Alors que, pour les inconnues h et Z, un schéma rétrograde est choisi (Équation 8).
Posons :
Ce qui donne :
De même, nous obtenons :
2.6 Discrétisation de l’équation de continuité solide
L’équation d’Exner 2 se réécrit en différences finies selon l’équation 13 :
De nombreuses formules empiriques sont proposées pour modéliser le transport par charriage. Chacune d’elles présente un intérêt pratique en absence de jaugeages, mais nécessite d’être vérifiée par des mesures de terrain en matière de pente et de granulométrie. La formule de charriage d’Einstein-Brown (GRACIA, 1982), qui tient compte de la vitesse d’écoulement, est retenue (Équation 14).
où : F, facteur dépend du diamètre d50, diamètre moyen des grains sédimentaires correspondant à 50 % du tamisât et Ss = ρs (masse volumique du sédiment / ρo (masse volumique de l'eau).
La résolution de l’expression de qs en modèle puissance donne des équations algébriques non linéaires, engendrant des difficultés en posttraitement; la convergence en calcul numérique est un grand problème, l’erreur d’itération augmente avec le nombre de boucles nécessaire à cette dernière. Pour éviter une telle situation, la linéarisation de l’équation 14, seule équation présentant une puissance supérieure à un, est nécessaire. Le système résultant est linéaire, résolu par la méthode « Élimination de Gauss ».
Alors :
De même :
Posons :
et
Il en résulte des équations discrétisées en différences finies avec un schéma implicite (Équation 19).
Si, les expressions données par les équations 11 et 12 sont remplacées dans les équations 6 et 19, deux équations à résoudre simultanément sont obtenues :
avec :
Les deux équations complètement discrétisées, appliquées de façon systématique à tout point de maillage, forment cette matrice. Les ![]() sont la solution de cette matrice [A] (2n x 2n). Qlin, qsin, Qlout, qsout sont les débits liquides et les débits solides à l’entrée et la sortie du tronçon étudié (Figure 4).
sont la solution de cette matrice [A] (2n x 2n). Qlin, qsin, Qlout, qsout sont les débits liquides et les débits solides à l’entrée et la sortie du tronçon étudié (Figure 4).
Figure 4
Système algébrique [A] écrit pour les différentes sections d’un tronçon.
Algebraic system [A] written for different sections of a river reach.
3. Application sur le système barrage-cours d’eau (SMBA-oued Mina)
Le tronçon barrage SMBA-Cours d’eau oued Mina convient à ce type de modélisation, son profil longitudinal est muni de plusieurs profils en travers (Figure 5), avec une vingtaine de sections transversales non uniformément réparties. Étant donné que le maillage est uniforme, le choix conditionné des profils en travers est fait à la base d’un pas régulier.
Figure 5
Maillage du tronçon du système barrage-cours d’eau.
Networking of the system consisting of the dam and the river channel.
Les paramètres géométriques d’une section naturelle sont résumés dans le tableau 1.
Tableau 1
Fonctions de corrélation de type polynomiale pour les paramètres géométriques d’une section exemple.
Polynomial correlation functions for the geometric parameters of a typical section.
3.1 Conditions aux limites
Le tronçon étudié est contrôlé, à son amont, par la station d’Oued El Abtal, disposant d’une série d’apports allant de 1979/80 jusqu'à 2003/04. Le barrage constitue la deuxième section de contrôle (section de sortie), les différents paramètres sont connus à cet endroit : le niveau initial du lit et les débits sortant durant toute la période de son exploitation, BOUHENICHE (2005). Pour la phase solide, les conditions aux limites à l’extrémité amont sont déduites de celles de la phase liquide, la formule de charriage utilisée est fonction de la vitesse d’écoulement liquide. À la sortie (extrémité avale), le débit solide sortant est nul; ce barrage n’a jamais eu d’opération de curage.
3.2 Simulation des dépôts aux différentes périodes d’exploitation et discussion des résultats
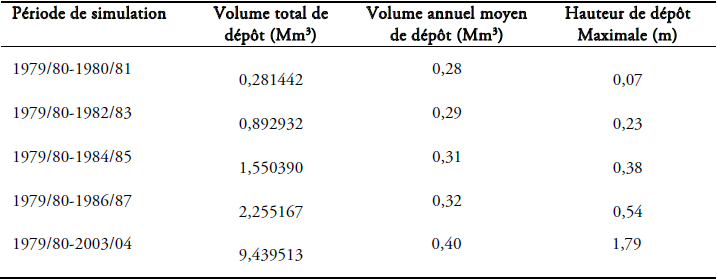
La simulation des dépôts à diverses périodes d’exploitation nécessite un fond et une ligne d’eau initiale. Les côtes du fond avant la mise en eau (1978) sont prises comme données initiales (ANB, 1979), bien que la ligne d’eau soit prise juste après le remplissage du barrage (1980). En raison de la disponibilité des mesures de dépôt, évaluées par le biais de la bathymétrie (1986 et 2003), les simulations sont faites sur différentes périodes incluant celles de sept et 24 ans (Tableau 2).
Tableau 2
Volume des dépôts pour différentes périodes de simulation.
Deposit volume for different periods of simulation.
Au vu du tableau 2, l’accumulation moyenne des dépôts passe de 0,281 à 0,4 Mm3 respectivement pour une année et pour la période 1979/80-2003/04, soit un dépôt de sédiment de 1,8 m de hauteur.
Les figures 6, 7 et 8 représentent des profils longitudinaux du système barrage-cours d’eau permettant une comparaison entre l’état initial et l’état final du lit.
Figure 6
Profile longitudinal du system SMBA-Oued Mina.
Longitudinal profile for the system SMBA-Oued Mina.
Figure 7
Simulation sept ans sur le system SMBA-Oued Mina.
Simulation for 7 years for the system SMBA-Oued Mina.
Figure 8
Simulation 24 ans sur le system SMBA-Oued Mina.
Simulation for 24 years for the system SMBA-Oued Mina.
Les résultats obtenus ne confirment pas les dires de la CIGB (Commission Internationale des Grands Barrages). Ils contrarient aussi les conclusions d’une étude de l’état d’envasement de 15 barrages de l’Algérie du Nord (BOUHENICHE, 2001), affirmant que la vitesse d’envasement décroît au cours des années d’exploitation. Reste à éclairer que ceci n’est pas une règle ou une loi, ce n’est qu’une conclusion obtenue dans un espace et une période définis. Elle sert ici à démontrer que cette retenue se comporte différemment de son environnement.
3.4 Comparaison avec la bathymétrie de 1986 et 2003
Le volume simulé des dépôts, sur la période de 1979/80-1986/87, est estimé à 2,255 Mm3, soit environ le 1/3 de celui enregistré par la bathymétrie qui est de 9 Mm3. La hauteur maximale des dépôts trouvée par la simulation est ∆ZF = 0,543 m, elle est enregistrée au tronçon 8, alors que la bathymétrie confirme une autre valeur ∆ZF = 1,6 m pour ladite section (Figure 7). Comme cette simulation ne concerne que le transport par charriage, le volume simulé rapporté au volume réel est de 25,05 %. Celui ci représente la contribution de ce mode de transport dans le dépôt enregistré pour cette période, confirmant les résultats des travaux de recherche de TOUAIBIA (2000) dans ce bassin. Dans la cuvette du barrage, le dépôt est dû aux deux modes de transport (charriage + suspension) dont la part de la suspension est de 75 %.
Après 24 ans d’exploitation, selon la bathymétrie, 84 Mm3 se sont déposés, soit une augmentation 9,33 fois plus grande que le volume déposé durant les sept premières années. Par contre, la simulation donne un volume de 9,976 Mm3, soit un rapport simulé/réel égal à 0,1187, c'est-à-dire que la contribution du charriage pour cette période est passée de 25,05 % à 11,87 %. La hauteur maximale simulée de dépôt est égale à 1,87 m. Une comparaison détaillée de cette simulation avec le levé bathymétrique ne peut être faite car ce dernier ne dispose pas de profil en long. Cette bathymétrie a évalué le volume des dépôts seulement. Les deux simulations confirment que les trois derniers sous-tronçons sont les plus touchés par le dépôt, appuyées par l’analyse détaillée de la bathymétrie de 1986.
4. Conclusion
L’analyse détaillée des résultats a montré le comportement de cette retenue de barrage. Durant la période 79/80-86/87, le dépôt simulé est de 2,255 Mm3, soit 0,95 % de la capacité initiale de stockage perdue, ce qui signifie une perte moyenne annuelle d’environ 0,31 Mm3. Le volume de dépôt mesuré par bathymétrie (9 Mm3) montre une contribution du charriage évaluée à 25,05 % dans le dépôt total. Durant la période 79/80-03/04, il s’est accumulé 84 Mm3, une perte annuelle accrue moyenne de 3,5 Mm3, soit trois fois la moyenne des sept premières années. La simulation sur cette période n’a pas suivi cette tendance, le volume déposé est égal à 9,976 Mm3, ce qui signifie une chute de la contribution du charriage à 11,87 %. De cette comparaison, il en ressort l’existence d’une différence entre les volumes simulés et mesurés, un comblement croissant en temps et que la partie inférieure du réservoir est la plus touchée par ce comblement. Certes, le modèle numérique nécessite une amélioration pour qu’il puisse prendre en compte les apports latéraux. L’autre voie consiste en l’amélioration de la qualité des données géométriques par un raffinage du maillage et par l’utilisation des fichiers de données au lieu du recours aux fonctions d’interpolation. Indépendamment de ces considérations topographiques, un complément intéressant peut être apporté au code de calcul. Une répartition des sédiments dans la section en travers sera un atout prometteur pour le calcul des volumes.
Parties annexes
Références bibliographiques
- ANB (Agence Nationale des Barrages) (1979). Rapport synthèse de l’avant-projet détaillé : projet de Barrage de Sidi Mohamed Ben Aouada. Ministère des Ressources en eau, Algérie.
- BOUHENICHE, S. (2001). Contribution à l’étude de l’état d’envasement des barrages de l’Algérie du Nord. Mémoire d’ingénierie d’État en Hydraulique. École nationale supérieure d’hydraulique, Blida. Algérie,120 p.
- BOUHENICHE, S. (2005). Contribution en une approche numérique de la modélisation du système barrage-cours d’eau, transport solide-déposition : Cas du barrage de Sidi M’hamed Benaouda sur l’Oued Mina. W. Relizane. Mémoire de magister, École Nationale Polytechnique, Alger, Algérie, 92 p.
- GRACIA, S. (1982). Mathematical model for simulation of delta formation and erosion down stream of reservoir. Dans : ICOLD Congress Q54, R8, Rio de Janeiro, Brésil.
- GRAF, W.H. et M.S. ALTINAKAR (1993). Hydraulique fluviale, écoulement permanent uniforme et non uniforme. Tome 1, Presses polytechnique et universitaires romandes, Lausanne, Suisse.
- GRAF, W.H. et M.S. ALTINAKAR (1996). Hydrodynamique une introduction. Presses polytechnique et universitaires romandes, Lausanne, Suisse.
- TOUAIBIA, B. (2000). Érosion - Transport solide - Envasement de barrage. Cas du bassin versant de la Mina dans la Wilaya de Relizane. Thèse de Doctorat d’État, Institut National Agronomique, Alger, Algérie, 181 p.
Liste des figures
Figure 1
Algorithme de la modélisation couplée.
Coupled modeling algorithm.
Figure 2
Volume de contrôle pour l’équation de continuité.
Control volume for the liquid-phase continuity equation.
Figure 3
Volume de contrôle pour l’équation dynamique.
Control volume for the momentum equation.
Figure 4
Système algébrique [A] écrit pour les différentes sections d’un tronçon.
Algebraic system [A] written for different sections of a river reach.
Figure 5
Maillage du tronçon du système barrage-cours d’eau.
Networking of the system consisting of the dam and the river channel.
Figure 6
Profile longitudinal du system SMBA-Oued Mina.
Longitudinal profile for the system SMBA-Oued Mina.
Figure 7
Simulation sept ans sur le system SMBA-Oued Mina.
Simulation for 7 years for the system SMBA-Oued Mina.
Figure 8
Simulation 24 ans sur le system SMBA-Oued Mina.
Simulation for 24 years for the system SMBA-Oued Mina.
Liste des tableaux
Tableau 1
Fonctions de corrélation de type polynomiale pour les paramètres géométriques d’une section exemple.
Polynomial correlation functions for the geometric parameters of a typical section.
Tableau 2
Volume des dépôts pour différentes périodes de simulation.
Deposit volume for different periods of simulation.





![Système algébrique [A] écrit pour les différentes sections d’un tronçon.](/fr/revues/rseau/2013-v26-n1-rseau0508/1014916ar/media/5012824n.jpg)