Résumés
Abstract
In this work, we study optimal strategies of wastewater reuse for refilling Jaunay Lake (a water reservoir located on the French western coast) which shows an alarming volume reduction due to the human water intake. To grasp the multiple issues to ascertain the appropriate location for the reused water discharge, mathematical modelling is particularly adapted for testing different conditions (physical, meteorological) and optimizing the system to achieve targets (maximum allowable concentration of pollutant for drinking water and recreational uses). We focus on modelling the distribution of a generic pollutant in the reservoir, which is expected to vary with time and space. The model assumes that the reservoir volume stays constant (because the flow rates at the refilling and removal points are considered to be quasi-identical), the density of the pollutant is smaller than that of the reservoir water (so that the pollutant remains at the top level of the water column) and its dynamics is influenced by two main effects: wind and water currents. The model accounts for the reservoir geometry, the operating conditions of the transfer pipes (input and output) and real data regarding chronicles of wind velocity and river flow. Then, we tackle a multi-optimization problem which aims to find optimal refilling locations which reduce the pollutant concentration at two strategic regions of the reservoir. A Pareto front is presented as a decision-tool to choose the optimal strategy according to different water quality criteria.
Keywords:
- water resources management,
- wastewater reuse,
- pollutant propagation,
- mathematical modelling,
- multi-objective optimization
Résumé
Dans ce travail, nous étudions des stratégies optimales de réutilisation d’eaux usées traitées pour le remplissage du lac de Jaunay (un réservoir d'eau situé sur la côte ouest-française), qui montre une réduction de volume alarmante en saison estivale due aux prélèvements anthropiques. Afin d’appréhender les multiples contraintes pour déterminer l'emplacement approprié du point de rejet, la modélisation informatique est particulièrement adaptée pour tester différentes conditions (physiques, météorologiques) et optimiser le système pour atteindre des cibles (concentration maximale du polluant pour de la production d'eau potable et des activités récréatives). Nous nous concentrons sur la modélisation de la distribution d'un polluant générique dans le réservoir qui varie en temps et en espace. Le modèle suppose que le volume du réservoir reste constant (en considérant que les débits aux points du rejet et de la prise d’eau sont quasiment identiques). La densité du polluant est supposée inférieure à celle de l'eau (donc le polluant reste à la surface de la colonne d’eau) et sa dynamique est influencée par deux effets principaux : les courants d’eau et le vent. Le modèle tient compte de la géométrie du réservoir, des conditions du pompage (en entrée et en sortie) et des données réelles concernant les chroniques du vent et du débit de la rivière. Ensuite, nous abordons un problème d’optimisation multiobjectif qui vise à trouver des emplacements optimaux de recharge qui réduisent la concentration du polluant dans deux régions stratégiques du réservoir. Un front de Pareto est présenté comme un outil de décision qui permet de choisir la stratégie optimale en fonction des différents critères sur la qualité de l'eau.
Mots-clés :
- gestion des ressources en eau,
- réutilisation des eaux usées traitées,
- propagation de polluant,
- modélisation informatique,
- optimisation multiobjective
Corps de l’article
1. Introduction
The reuse of treated wastewater is already practiced in many countries, both in dry regions (e.g. Sahel, Golf Persian, etc.) and more widely regions with high water stress index (e.g. around the Mediterranean), a frequent use being agricultural irrigation. Its use to refill reservoirs (lakes, ponds, aquifers, etc.) is not widely practiced or currently forbidden in countries like France. Indeed, adding treated wastewater may modify the composition of the water reservoir (chemically and biologically) and lead to health risks. A possible solution could be to purify the wastewater to a high quality (such as drinking quality), this approach being the safest but not economically viable due to advanced treatment costs. Seeking the best compromise between the exploitation of available treated water and the restrictions on its use is currently mobilizing researchers and policy makers to propose solutions in order to face water scarcity (ALCALDE-SANT and GAWLIK 2014; CONDOM et al., 2013).
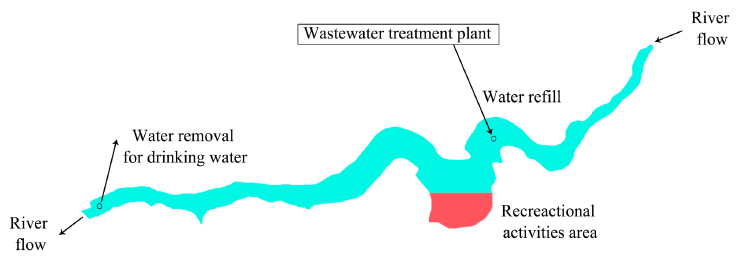
In this work, we aim to propose optimal strategies of wastewater reuse for refilling a generic water reservoir and then apply the proposed methodology to a concrete case study suggested by Vendée Eau. Vendée Eau is a nonprofit public body in charge of the drinking water supply on the French western coast, which produces drinking water mainly from surface resources. Particularly, it is in charge of the water intake in Jaunay Lake (a fresh water reservoir of 3 700 000 m3), its purification and its distribution to neighboring populations. This water intake results in a reduction of the lake volume, which becomes alarming in dry seasons when its volume may decrease to half of its capacity. In order to preserve the lake water volume to a desired value, Vendée Eau proposes to refill the lake with reused water, coming from a coastal wastewater treatment plant, so that the volume of the lake stays roughly constant during the refill operation (see figure 1 for a detailed description of the water balance occurring in Jaunay Lake). The reused water is obtained after adding a tertiary treatment unit and it may still contain pollutant. Our objective is to find an optimal location of the refilling point such that the pollutant concentration is minimized at the region of the lake devoted to recreational activities, and at the same time maintained under a desired threshold near the removal point. On account of the absence of regulations and unprecedented cases of indirect potable reuse in France, Vendée Eau envisions the implementation of a 1:4 scale demonstrator during the 2018-2024 period including tertiary treatment unit, transfer pipe and discharge zone.
Figure 1
Schematic representation of the Jaunay Lake configuration
Représentation schématique de la configuration du lac de Jaunay
To grasp the multiple issues to ascertain the appropriate location for the reused water discharge, mathematical modelling is particularly adapted for describing the water quality under different system and meteorological conditions (ALAVANI et al., 2010; BARBIER et al., 2016; GAJARDO et al., 2017; RAPAPORT et al., 2014). Our strategy resides in introducing a mathematical model which describes the evolution of the water quality in the reservoir, carrying out numerical simulations and solving the desired optimization problem with an appropriate optimization algorithm. In this work, we focus on modelling the distribution of a generic pollutant in the reservoir through the refilling process with treated water from a wastewater treatment plant. Following ALAVANI et al. (2010) and references thereinafter, we assume that the density of the pollutant is smaller than that of the lake water (so the pollutant remains at the top level of the water column). Moreover, we consider that the reservoir volume remains roughly constant (because the flow rates at the refilling and removal points are assumed quasi-identical). Furthermore, we consider that two main effects influence the pollutant distribution: wind and water currents, the latter resulting from the pumping processes and the discharge of Jaunay River into the reservoir. In order to tackle the proposed bi-objective optimization problem, which aims to control the water quality at two different lake sectors, we present a Pareto front showing how improving one objective is related to deteriorating the second one. This methodology has been broadly used when solving multi-objective problems for water management (AL-ZAHRANI et al., 2016; MORTAZAVI et al., 2012; VEMURI 1974; ZHANG et al., 2014), since it provides a decision-tool to a posteriori help in choosing the optimal strategy according to different water quality criteria.
The article is organized as follows: in section 2 we introduce the model describing the distribution of a generic pollutant in a large water reservoir through the refill process. In section 3 we state the optimization problem which aims to preserve the water quality at two specific regions by choosing a suitable refilling location. In section 4, we explain the numerical experiments carried out for the optimization problem and show the results obtained for the Jaunay case study.
2. Mathematical modelling
Let us denote by Ω ⊂ ℝ2 the spatial domain describing the surface of the water resource (see figure 2 for a physical description). The boundary of the domain, denoted by Ω, can be seen as ∂Ω = Γin ∪ Γout ∪ Γwall, where Γin and Γout are the parts of the boundary through which the water enters and leaves the reservoir due to natural flow, respectively, and Γwall = ∂Ω / Γin ∪ Γout is the part of the boundary where null flux is considered. The refilling and removal locations are denoted by Γref and Γrem, respectively. We denote by Ωcrit ⊂ Ω the critical area of the domain usually devoted to recreational activities.
Figure 2
Domain representation of the Jaunay Lake surface geometry
Représentation de la géométrie de la surface du lac de Jaunay
Following ALAVANI et al. (2010), we assume that the density of the pollutant is smaller than that of the lake water, so that it remains at the top level of the water column. Additionally, we consider that the possible changes on the lake volume occurring along the process are negligible.
We denote by c(x, t) the pollutant superficial concentration, measured as the volume of pollutant per surface area at (x, t) ∈Ω (0, T), where T is the final time for which we want to model the process. We consider that the evolution of c is governed by four main effects, namely:
The diffusion of the pollutant.
The wind induced transport.
The water currents induced transport.
The spill and removal of pollutant resulting from the pumping processes.
Under these assumptions, the space-time distribution of c is governed by the following advection-diffusion type equation:
where D is the diffusion coefficient of the pollutant in the reservoir water, ![]() is the wind velocity vector and α is a drag factor measuring the percentage of the wind speed inducing the pollutant transport. The water currents velocity vector, denoted by
is the wind velocity vector and α is a drag factor measuring the percentage of the wind speed inducing the pollutant transport. The water currents velocity vector, denoted by ![]() , is computed by solving the well-known Navier-Stokes equations (GLOWINSKI, 2013) taking into account the lake geometry, the river velocity at its mouth and the pumping velocities at the removal and refilling locations. Furthermore, we denote by c0, cref and cin the pollutant concentration in the lake at the beginning of the process, the pollutant concentration at the refilling location Γref and the pollutant concentration at the river mouth Γin, respectively.
, is computed by solving the well-known Navier-Stokes equations (GLOWINSKI, 2013) taking into account the lake geometry, the river velocity at its mouth and the pumping velocities at the removal and refilling locations. Furthermore, we denote by c0, cref and cin the pollutant concentration in the lake at the beginning of the process, the pollutant concentration at the refilling location Γref and the pollutant concentration at the river mouth Γin, respectively.
3. Optimization problem
We consider the optimization problem consisting in minimizing the amount of pollutant in the critical region Ωcrit, while the pollutant concentration is maintained under a desired threshold ![]() at the removal point Γrem, by choosing a suitable refilling location Γref. Given the final T > 0 for which we want to model the process, the optimization problem can be formulated as follows:
at the removal point Γrem, by choosing a suitable refilling location Γref. Given the final T > 0 for which we want to model the process, the optimization problem can be formulated as follows:
where JT is defined as the amount of pollutant in Ωcrit along the process,
and ![]() denotes the maximum pollutant concentration reached at Γrem,
denotes the maximum pollutant concentration reached at Γrem,
4. Numerical experiments
In this section, we first introduce the numerical solver used for computing the solutions of the system (Equation 1) and describe the considered numerical experiments based on the optimization problem (Equation 2). Then, in section 4.2 we analyze the effect of the wind and water currents on the pollutant distribution for the Jaunay case study. Section 4.3 presents the optimization results and outline the influence of setting different water quality thresholds on the obtained optimal refilling location for the Jaunay case study.
4.1 Numerical implementation of the model
The solution of equation 1 was computed using the software COMSOL Multiphysics 5.3 (www.comsol.com) based on the Finite Element Method. Model variables (Equations 3 and 4) were estimated using the functions Domain Integration (based on a trapezoidal approximation of the integral) and Boundary Maximum of COMSOL, respectively. The numerical experiments were carried out in a 2.8 Ghz Intel i7-930 64 bits with 12 Gb of RAM. We used a triangular mesh with around 14 000 elements. Depending on the considered case (detailed below), each function evaluation in equation 2 may take from 20 min up to 4 h.
Model parameters were taken following the data provided by Vendée Eau. The period of time for which we have modeled the process is 1 June 2016 - 31 August 2016. In order to compute the velocity vector ![]() we assumed that the river enters in the lake with a flow rate of 1.96 x 10-3 (m3∙s-1), the flow rate of the pumping is 3.47 x 10-1 (m3∙s-1) and the physical pipe in charge of the pumping is a cylinder with a cross section of radius 3 m. Additionally, data regarding the wind velocity
we assumed that the river enters in the lake with a flow rate of 1.96 x 10-3 (m3∙s-1), the flow rate of the pumping is 3.47 x 10-1 (m3∙s-1) and the physical pipe in charge of the pumping is a cylinder with a cross section of radius 3 m. Additionally, data regarding the wind velocity ![]() was extracted from the free source COPERNICUS (http://marine.copernicus.eu/services-portfolio/access-to-products/). The pollutant was assumed to diffuse with rate D = 1.31 x 10-8 m2∙s-1 (HAMAM, 1987) and show a drag factor α = 2 x 10-3 (ALAVANI et al., 2010). At initial time, the pollutant concentration in the lake was taken constant with value c0 = 0.05 kg∙m-2. We assumed that the water entering the lake through the refilling pipe was charged with a pollutant concentration cref = 0.19 kg∙m-2, while the water entering the lake through the river was clean, i.e. cin = 0 kg∙m-2. The solution of equation 2 was approximated by taking 1 400 possible refilling locations uniformly distributed through the lake surface,
was extracted from the free source COPERNICUS (http://marine.copernicus.eu/services-portfolio/access-to-products/). The pollutant was assumed to diffuse with rate D = 1.31 x 10-8 m2∙s-1 (HAMAM, 1987) and show a drag factor α = 2 x 10-3 (ALAVANI et al., 2010). At initial time, the pollutant concentration in the lake was taken constant with value c0 = 0.05 kg∙m-2. We assumed that the water entering the lake through the refilling pipe was charged with a pollutant concentration cref = 0.19 kg∙m-2, while the water entering the lake through the river was clean, i.e. cin = 0 kg∙m-2. The solution of equation 2 was approximated by taking 1 400 possible refilling locations uniformly distributed through the lake surface, ![]() , and computing the objective values
, and computing the objective values ![]() (kg) and
(kg) and ![]() (kg∙m-2) (see equations 3-4 associated to each prospective location
(kg∙m-2) (see equations 3-4 associated to each prospective location ![]() , i = 1,..., 1400).
, i = 1,..., 1400).
4.2 Analysis of the wind and water current induced transport
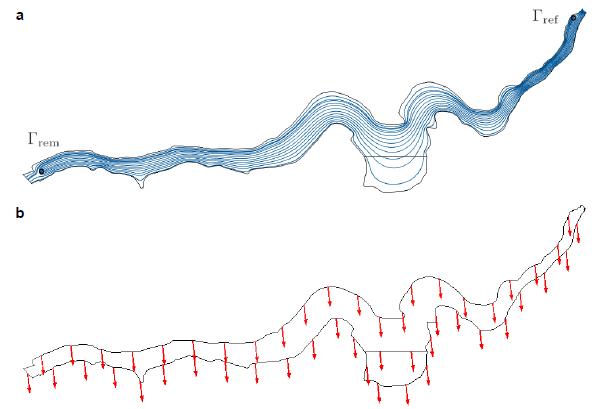
As explained in section 2, we assume that the pollutant transport is due by two main factors: water currents and wind. The water currents speed vector ![]() does not depend on time, since we consider that the river velocity and pumping flow rates are constant along the process. Figure 3a shows an example of the streamlines of vector
does not depend on time, since we consider that the river velocity and pumping flow rates are constant along the process. Figure 3a shows an example of the streamlines of vector ![]() (computed for a specific choice of refilling and removal locations) showing the direction in which a Lagrangian particle travels at any point in the lake surface. We observe that the trajectory of the particles follows the natural flow induced by the upstream river mouth. The removal pipe absorbs some of the particles while the rest leave the lake through the downstream lake boundary. On the other hand, real data seem to show that in the region of France where Jaunay Lake is located, the wind velocity vector
(computed for a specific choice of refilling and removal locations) showing the direction in which a Lagrangian particle travels at any point in the lake surface. We observe that the trajectory of the particles follows the natural flow induced by the upstream river mouth. The removal pipe absorbs some of the particles while the rest leave the lake through the downstream lake boundary. On the other hand, real data seem to show that in the region of France where Jaunay Lake is located, the wind velocity vector ![]() usually has a direction from north-west to south-east, as depicted in figure 3b. When this occurs, the wind pushes the pollutant to the south eastern zones of the lake (as for instance the recreational activities area Ωcrit).
usually has a direction from north-west to south-east, as depicted in figure 3b. When this occurs, the wind pushes the pollutant to the south eastern zones of the lake (as for instance the recreational activities area Ωcrit).
Figure 3
Analysis of the wind and water current velocity vectors for Jaunay Lake: a) water current streamlines associated to an specific choice of Γref and Γrem, b) usual wind directions registered in the lake region
Analyse des vecteurs de vitesse du courant d'eau et du vent pour le lac de Jaunay : a) lignes de courant d'eau associées à un choix spécifique de Γref and Γrem, b) directions habituelles du vent enregistrées dans la région du lac
4.3 Optimization results
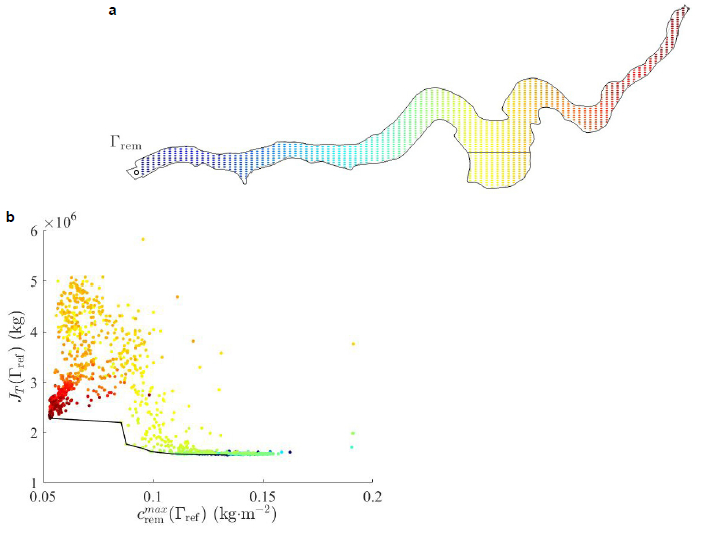
The bi-objective optimization problem (Equation 2) may have multiple optimal solutions depending on how restrictive are the constraints in each of the objectives (in our case, reducing the pollutant concentration at areas Γrem and Ωcrit). In this case, a usual methodology to visualize the possible optimization results is to plot the Pareto front (AUBIN, 1984), a curve that informs the decision-maker how improving one objective is related to deteriorating the second one while moving along the curve. In figure 4a, the tested refilling locations ![]() are plotted such that the distance to the removal point decreases from blue to red. In figure 4b, each depicted point corresponds to the pair of objective values,
are plotted such that the distance to the removal point decreases from blue to red. In figure 4b, each depicted point corresponds to the pair of objective values, ![]() , obtained for an specific refilling location
, obtained for an specific refilling location ![]() in figure 4a, from which the color plot is inherited with a view to easily associate distinct ranges of the objective values with specific sectors in the lake. The Pareto front is depicted with a black curve. As expected, numerical simulations seem to show that refilling locations near the removal point Γrem reduce the amount of pollutant at the recreational activities area Ωcrit. On the contrary, refilling locations near the river mouth induce low pollutant concentration at the removal point. This representation may help the decision makers to balance their choice between the two criteria.
in figure 4a, from which the color plot is inherited with a view to easily associate distinct ranges of the objective values with specific sectors in the lake. The Pareto front is depicted with a black curve. As expected, numerical simulations seem to show that refilling locations near the removal point Γrem reduce the amount of pollutant at the recreational activities area Ωcrit. On the contrary, refilling locations near the river mouth induce low pollutant concentration at the removal point. This representation may help the decision makers to balance their choice between the two criteria.
Figure 4
Graphical interpretation of a) tested refilling locations  used to obtain b) the objective values
used to obtain b) the objective values  ,
,  in equation 2. The black curve represents the Pareto front
in equation 2. The black curve represents the Pareto front
Interprétation graphique a) des emplacements de recharge testés  utilisés pour obtenir b) les valeurs des objectifs
utilisés pour obtenir b) les valeurs des objectifs  ,
,  dans l’équation 2. La courbe noire répresente le front de Pareto
dans l’équation 2. La courbe noire répresente le front de Pareto
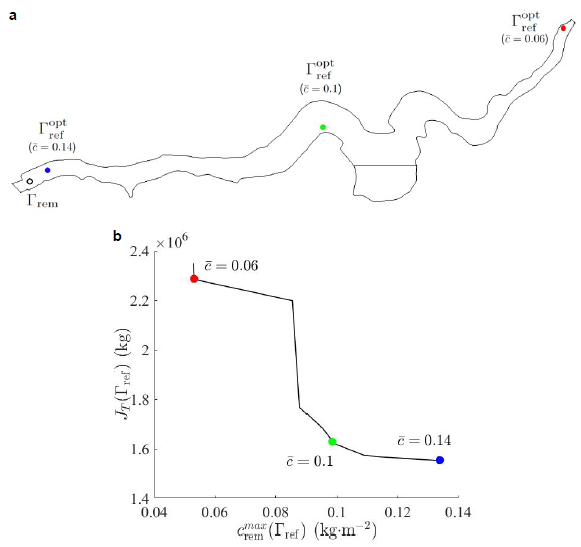
Figure 5a shows the optimal refilling locations, solution of equation 2, obtained when setting ![]() ∈ {0.06, 0.1, 0.14} kg∙m-2, that is, obtained when imposing three different water quality thresholds at the removal point. Figure 5b plots the points of the Pareto front corresponding to the optimal locations in figure 5a. By choosing the most restrictive threshold,
∈ {0.06, 0.1, 0.14} kg∙m-2, that is, obtained when imposing three different water quality thresholds at the removal point. Figure 5b plots the points of the Pareto front corresponding to the optimal locations in figure 5a. By choosing the most restrictive threshold, ![]() = 0.06, we aim a high quality effluent at the removal point Γrem, while setting
= 0.06, we aim a high quality effluent at the removal point Γrem, while setting ![]() = 0.14, we priorize the water quality at the region of the lake devoted to recreational activities, Ωcrit. The intermediate constraint
= 0.14, we priorize the water quality at the region of the lake devoted to recreational activities, Ωcrit. The intermediate constraint ![]() = 0.1 represents a trade-off for which the pollutant concentration is controlled at both areas Γrem and Ωcrit.
= 0.1 represents a trade-off for which the pollutant concentration is controlled at both areas Γrem and Ωcrit.
Figure 5
Graphical interpretation of the optimization results solution of equation 2 when  ∈ {0.06, 0.1 0.14} kg∙m-2: a) optimal refilling locations
∈ {0.06, 0.1 0.14} kg∙m-2: a) optimal refilling locations  , b) objective values
, b) objective values  ,
,  associated to these optimal refilling locations. The black curve represents the Pareto front
associated to these optimal refilling locations. The black curve represents the Pareto front
Interprétation graphique des résultats d'optimisation solution de l’équation 2 lorsque  ∈ { 0,06, 0,1 0,14} kg∙m-2 : a) emplacements optimaux de recharge
∈ { 0,06, 0,1 0,14} kg∙m-2 : a) emplacements optimaux de recharge  et b) valeurs des objectifs
et b) valeurs des objectifs  ,
,  associées à ces emplacements optimaux. La courbe noire représente le front de Pareto
associées à ces emplacements optimaux. La courbe noire représente le front de Pareto
Finally, figure 6 represents the pollutant distribution at final time (31 August 2016) obtained with the optimal refilling locations in figure 4a. As explained in section 4.2, one can observe that due to the wind effect, the pollutant concentration is notably accumulated at the southern areas of the lake. Indeed, high pollutant concentrations are reported at Ωcrit whenever the refilling pipe is placed at the right hand side of this region. As a result, one can conclude that in order to reduce the pollutant concentration at areas Γrem and Ωcrit, the refilling pipe must be placed as far as possible from Γrem and at the left hand side of Ωcrit.
Figure 6
Pollutant concentration c (kg∙m-2) at the simulated final time (31 August 2016) associated to the optimal refilling locations  solution of equation 2 when
solution of equation 2 when  = a) 0.06, b) 0.1, c) 0.14 kg∙m-2
= a) 0.06, b) 0.1, c) 0.14 kg∙m-2
Concentration du polluant c (kg∙m-2) à la date finale simulée (31 août 2016) associée aux emplacements optimaux de recharge  solution de l’équation 2 lorsque
solution de l’équation 2 lorsque  = a) 0,06, b) 0,1, c) 0,14 kg∙m-2
= a) 0,06, b) 0,1, c) 0,14 kg∙m-2
5. Conclusions
We have proposed a methodology to determine optimal strategies for refilling water resources with reused water still containing some pollutant. The methodology has been applied in the case of Jaunay Lake, a water reservoir located on the French western coast, which shows an alarming volume reduction due to the human water intake. The main objective was to find optimal refilling locations ensuring that a water quality threshold was maintained at the region of the lake devoted to recreational activities but also at the intake location, while maintaining the volume of the lake almost constant.
We have used a mathematical model, based on a partial differential equation of advection-diffusion type, which describes the distribution of a generic pollutant through the lake. The model assumes that pollutant remains at the surface of the water reservoir and the evolution of its distribution is mainly influenced by wind and lake water currents. Using the Finite Element Method, we have numerically computed the transient pollutant distribution associated to a particular refilling location. A total of 1 400 prospective refilling positions have been computationally tested and a Pareto front has been obtained, informing the policy-maker about the trade-offs among the water quality at both lake regions. Besides, real data seem to show that, in the area of France where Jaunay Lake is located, the wind velocity usually has a direction from north-west to south-east, which results in an accumulation of pollutant at the south-eastern zones of the lake (as for instance the recreational activities area). One concludes that, in order to achieve a reasonable trade-off among the two water quality objectives, the refilling pipe must be positioned as far as possible from the intake location and downstream the leisure region. Vendée Eau, the nonprofit public body in charge of the water management in Jaunay Lake, envisions the implementation of a 1:4 scale demonstrator during the 2018-2024 period based on the optimization results presented here.
In this work, we have considered that the volume of the lake remains roughly constant through the refilling process. Dropping this assumption is a matter of future work and the ultimate goal of this project, since we aim at decreasing the speed of the volume reduction more than at maintaining the volume to a constant value.
Parties annexes
Acknowledgements
The authors thank the LabEx Numev (project ANR-10-LABX-20) incorporated into the I-Site MUSE for the postdoctoral grant of the first author at Mistea lab, Montpellier, France. We are grateful to the association of municipalities Vendée Eau and the Saur Group for their assistance with data acquisition in Jaunay Lake and fruitful exchanges.
References
- ALAVANI C., R, GLOWINSKI, S, GOMEZ, B, IVORRA, P, JOSHI and A.M. RAMOS (2010). Modelling and simulation of a polluted water pumping process. Math. Comput. Model., 51, 461-472.
- ALCALDE-SANT L. and B. GAWLIK (2014). Water reuse in Europe within guidelines, needs and barriers to innovation. A synoptic overview. JRC Science and policy reports, Publications Office of the European Union, JRC92582, Luxembourg, 51 p.
- AL-ZAHRANI M., A. MUSA and S. CHOWDHURY (2016). Multi-objective optimization model for water resource management: a case study for Riyadh, Saudi Arabia. S. Environ. Dev. Sustain., 18, 777-798.
- AUBIN J.P. (1984). L'analyse non linéaire et ses motivations économiques. Coll. Mathématiques Appliquées pour la Maîtrise, Masson, France, 214 p.
- BARBIER S., A. RAPAPORT and A. ROUSSEAU (2016). Modeling of biological decontamination of water in natural resource environment and related feedback strategies. J. Sci. Comput., 68, 1267-1280.
- CONDOM N., B. MOLLE, S. TOMAS, Y. OLIVIER, M. AUDOUARD and J. GRANIER (2013). La réutilisation maîtrisée des eaux usées : approfondir les connaissances pour lever les freins et relever les défis. Sci. Eaux Territoires, 11, 54-57.
- GAJARDO P., J. HARMAND, H. RAMIREZ, A. RAPAPORT, V. RIQUELME and A. ROUSSEAU (2017). Modeling and control of in-situ decontamination of large water resources. ESAIM Proc. Surv., 57, 70-85.
- GLOWINSKI R. (2013). Numerical methods for nonlinear variational problems. Scientific computation. Springer-Verlag Berlin Heidelberg, New York, 493 p.
- HAMAM S.E.M. (1987). Diffusion of crude oil. J. Environ. Sci. Health, 105, 445-456.
- MORTAZAVI M., G. KUCZERA and L. CUI (2012). Multiobjective optimization of urban water resources: Moving toward more practical solutions. Water Resour. Res., 48, W03514.
- RAPAPORT A., A. ROUSSEAU and J. HARMAND (2014). A method of treating a fluid resource, computer program and associated processing module. Patent No. FA 78 4546 - EN 13 55129.
- VEMURI V. (1974), Multiple-objective optimization in water resource systems. Water Resour. Res., 10, 44-48.
- ZHANG W., C. WANG, Y. LI, P. WANG, Q. WANG and D. WANG (2014). Seeking sustainability: Multiobjective evolutionary optimization for urban wastewater reuse in China. Environ. Sci. Technol., 48, 1094-1102.
Liste des figures
Figure 1
Schematic representation of the Jaunay Lake configuration
Représentation schématique de la configuration du lac de Jaunay
Figure 2
Domain representation of the Jaunay Lake surface geometry
Représentation de la géométrie de la surface du lac de Jaunay
Figure 3
Analysis of the wind and water current velocity vectors for Jaunay Lake: a) water current streamlines associated to an specific choice of Γref and Γrem, b) usual wind directions registered in the lake region
Analyse des vecteurs de vitesse du courant d'eau et du vent pour le lac de Jaunay : a) lignes de courant d'eau associées à un choix spécifique de Γref and Γrem, b) directions habituelles du vent enregistrées dans la région du lac
Figure 4
Graphical interpretation of a) tested refilling locations  used to obtain b) the objective values
used to obtain b) the objective values  ,
,  in equation 2. The black curve represents the Pareto front
in equation 2. The black curve represents the Pareto front
Interprétation graphique a) des emplacements de recharge testés  utilisés pour obtenir b) les valeurs des objectifs
utilisés pour obtenir b) les valeurs des objectifs  ,
,  dans l’équation 2. La courbe noire répresente le front de Pareto
dans l’équation 2. La courbe noire répresente le front de Pareto
Figure 5
Graphical interpretation of the optimization results solution of equation 2 when  ∈ {0.06, 0.1 0.14} kg∙m-2: a) optimal refilling locations
∈ {0.06, 0.1 0.14} kg∙m-2: a) optimal refilling locations  , b) objective values
, b) objective values  ,
,  associated to these optimal refilling locations. The black curve represents the Pareto front
associated to these optimal refilling locations. The black curve represents the Pareto front
Interprétation graphique des résultats d'optimisation solution de l’équation 2 lorsque  ∈ { 0,06, 0,1 0,14} kg∙m-2 : a) emplacements optimaux de recharge
∈ { 0,06, 0,1 0,14} kg∙m-2 : a) emplacements optimaux de recharge  et b) valeurs des objectifs
et b) valeurs des objectifs  ,
,  associées à ces emplacements optimaux. La courbe noire représente le front de Pareto
associées à ces emplacements optimaux. La courbe noire représente le front de Pareto
Figure 6
Pollutant concentration c (kg∙m-2) at the simulated final time (31 August 2016) associated to the optimal refilling locations  solution of equation 2 when
solution of equation 2 when  = a) 0.06, b) 0.1, c) 0.14 kg∙m-2
= a) 0.06, b) 0.1, c) 0.14 kg∙m-2
Concentration du polluant c (kg∙m-2) à la date finale simulée (31 août 2016) associée aux emplacements optimaux de recharge  solution de l’équation 2 lorsque
solution de l’équation 2 lorsque  = a) 0,06, b) 0,1, c) 0,14 kg∙m-2
= a) 0,06, b) 0,1, c) 0,14 kg∙m-2