Résumés
Résumé
Le Cours de Linguistique Générale consacre deux chapitres à la phonologie sous les titres “Définition des phonèmes” et “Le Phonème dans la chaîne parlée”. Ces textes se présentent aujourd’hui sous le double aspect d’une question d’histoire des sciences non-résolue et d'une question théorique ouverte, l’irrésolution de la première masquant l’intérêt systémique de la seconde.
Critiqués dès 1930 par les théoriciens de l’École de Prague (Troubetzkoy, Jakobson), les Principes de Phonologie de Saussure ont perdu tout crédit scientifique et sont tombés dans l’oubli. La critique des Pragois est à la fois élogieuse et sévère. Tout en se réclamant de son caractère fondateur, ils reprochent à la théorie saussurienne d’être contradictoire, mêlant, selon leurs analyses, deux disciplines devant demeurer distinctes, la phonétique et la phonologie. Les contradictions relevées par les maîtres de l’École de Prague paraissent, en effet, évidentes. D’une part Saussure écrit : “L’essentiel de la langue est étranger au caractère phonique du signe linguistique” (CLG : 21) ou “la question de l’appareil vocal est secondaire dans le problème du langage” (CLG : 26); mais d’autre part, il affirme que “la liberté de lier les espèces phonologiques (phonèmes) est limitée par la possibilité de lier les mouvements articulatoires” (CLG : 79). On ne peut, en effet, soutenir la nécessité d’une distinction stricte entre traits différentiels de langue et mécanique articulatoire et, en même temps, affirmer que la délimitation des phonèmes dépend de contraintes de l’appareil vocal. Ainsi Troubetzkoy et Jakobson reprocheront-ils au maître genevois de réintroduire la phonétique dans le débat phonologique.
Mais il y a malentendu. En confrontant les critiques pragoises aux textes de Saussure, on découvre, à la place des contradictions attendues, la description d’un système double de catégories et de fonctions dont chaque partie, dûment développée, aboutit à une loi. La thèse de Saussure maintient strictement (mais subtilement) la distinction entre phonétique et phonologie, contrairement aux allégations des Pragois. Dans une lecture systémique des Principes de Phonologie de Saussure, nous n’avons trouvé ni les “contradictions” ni le “psychologisme naïf” ni non plus de “retour aux procédés de la phonétique motrice” que Jakobson avait critiqués. Il s’agit dans cet article de reconstruire et tester ce modèle saussurien discrédité. Les historiens des sciences auront alors à nous expliquer l’étonnante indifférence dans laquelle est tombée une analyse (si opérante et importante) placée au milieu du livre le plus lu de la linguistique générale.
Mots-clés :
- phonologie,
- systémique,
- valeurs pures,
- notation tabulaire numérale,
- clôture topique
Abstract
Ferdinand de Saussure’s Course in General Linguistics (CLG in French), edited and published by Charles Bally and Albert Sechehaye in 1916, contains two chapters on phonology : “Definition of the Concept of Phoneme” and “The Phoneme in the Spoken Chain”. These texts were criticised by Nicolas Troubetzkoy (1949) and Roman Jakobson (1976) and judged inconsistent and as a result lost their scientific credibility and are mostly forgotten today. Prague School criticism was simultaneously laudatory and harsh. Recognizing the highly original nature of Saussure’s contribution, it was criticized for being contradictory in its amalgamation of phonetics and phonology. And clearly, some passages from the Course in General Linguistics appear to support Troubetzkoy’s and Jakobson’s claim. Yet, this view rests on a misunderstanding.Close reading of Saussure shows rather that he sought to describe a double system of categories and functions uncovering a linguistic law. Saussure’s thesis strictly – but subtly – maintains the disctinction between phonectics and phonology, contrary to the assertions of the Prague linguists.
Indeed a systematic reading of Saussure’s Principes de phonologie shows no “contradiction”, no trace of any “naive psychologism”, nor a “return to procedures of motor phonetics” as Jakobson would have it. In this article, I therefore endeavor to reconstruct and test Saussure’s discredited model. I leave it to historians to explain how it is such a key and operational analysis set midway through the most widely read general linguistic treatise could have fallen into such indifference.
Keywords:
- Phonology,
- Systemics,
- Pure Values,
- Numeral Tabular Notation,
- Closure Principle
Corps de l’article
Le Cours de Linguistique Générale de Ferdinand de Saussure (ci-après, CLG) consacre deux chapitres à la phonologie sous les titres “Définition des phonèmes” et “Le Phonème dans la chaîne parlée”. Ces textes, édités à partir des trois conférences de F. de Saussure sur la Théorie de la Syllabe de 1897, se présentent aujourd’hui sous le double aspect d’une question d’histoire des sciences non-résolue et d’une question théorique ouverte, l’irrésolution de la première masquant l’intérêt systémique de la seconde.
Critiqués dès 1930 par les théoriciens de l’École de Prague (Troubetzkoy, Jakobson), les “Principes de Phonologie” du CLG ont perdu leur crédit scientifique et sont tombés dans l’oubli. La critique des Pragois est à la fois élogieuse et sévère. Tout en se réclamant de son caractère fondateur, ils reprochent à la théorie saussurienne d’être contradictoire, mêlant, selon leurs analyses, deux disciplines devant demeurer distinctes, la phonétique et la phonologie. “Comment saisir l’extrême malentendu qui domine les raisonnements sur le langage (Saussure 2002 : 42)? Car il y a malentendu. En confrontant les critiques pragoises aux textes du CLG, on découvre, à la place des contradictions attendues, la description d’un système double, de catégories et de fonctions, dont chaque partie, dûment développée, aboutit à une loi. La thèse saussurienne maintient strictement (mais subtilement) la distinction entre phonétique et phonologie, contrairement aux allégations des Pragois. Dans la lecture systémique des “Principes de Phonologie” du CLG présentée ici, nous n’avons trouvé ni les “contradictions” ni le “psychologisme naïf” ni le “retour aux procédés de la phonétique motrice” que Jakobson avait critiqués.
Saussure entreprend la construction des premiers éléments de l’architecture de la langue, la phonologie et le syllabaire (CLG). Sa démonstration n’est pas complète, mais les principes qu’il met en oeuvre sont solides et clairs, suffisamment, en tout cas, pour permettre la mise au jour deux lois systémiques qui confirment l’ancrage empirique de sa théorie et la précision de sa méthode. Il s’agit dans ce qui va suivre de reconstruire, pas à pas (et de prolonger jusqu’à son terme), la démonstration de Saussure, en se limitant au chapitre intitulé dans le CLG “Les espèces phonologiques”. Pour poursuivre ce travail constructiviste et le faire aboutir, il faut en conserver les principes et les méthodes sous peine d’une élaboration ad hoc, toujours possible, mais sans intérêt au regard de la question historique posée, à savoir : le programme de la Langue, Système de Valeurs Pures existe-t-il dans le corpus saussurien et, si oui, est-il scientifiquement légitime, c’est-à-dire évident, cohérent et pertinent aujourd’hui?
“Définition du phonème”[1]. Coupe physiophonétique
Telle qu’elle est présentée dans “Les espèces phonologiques”, la construction du système phonologique du français suit une progression qui peut s’avérer trompeuse et donner raison à ses détracteurs. Elle commence en prenant appui sur une coupe physiophonétique de l’appareil vocal. Les Pragois y ont vu, sans hésiter, une flagrante contradiction entre phonétique et phonologie.
Contrairement à l’apparence, l’appareil vocal n’est pas pour Saussure un générateur sonore signifiant, mais un résonateur catégorisé : “l’expiration, élément positif, qui intervient dans tout acte phonatoire, n’a pas de valeur différenciatrice”. Dans aucune langue, la distinction (générateur/résonateur) ne constitue un trait pertinent, semble-t-il.
Que je crie ou parle à voix normale, que je chuchote, que ma voix soit celle d’une fille ou d’un garçon, que je sois jeune ou vieux, les infinies variations de la voix, pertinentes comme “traits sémiématiques” (selon le vocabulaire de Damourette et Pichon), sont des différences indifférentes pour le système phonologique; la voix est une nécessité et parfois un art, mais n’est, en aucun cas, un facteur linguistique discriminant. “Ce n’est pas le son matériel, chose purement physique (qui vaut dans l’exercice de la langue) mais l’empreinte psychique de ce son (1916 [1972 : 98])”, empreinte uniquement constituée de différences qualitatives. Saussure enseigne que “l’essentiel de la langue est étranger au caractère phonique du signe linguistique” (1916 [1972 : 21]). En d’autres termes, il n’y a pas de phoné dans les phonèmes; les phonèmes ne sont pas des voix, mais des différenciateurs de sens[2].
On ne se pénètrera jamais assez de l’essence purement négative, purement différentielle, de chacun des éléments du langage auxquels nous accordons précipitamment une existence. Il n’y en a aucun dans aucun ordre, qui possède une existence supposée.
ibid. 2002 : 64-65
Si la propension de la phonétique est la production des sons de langage, celle de la phonologie est “l’oreille”, “l’empreinte psychique”, la prise en acte de la parole; entre ces deux sciences, il faut inverser les rôles : respectivement parler ou entendre.
De la coupe physiophonétique à la tabulation par idéogrammes
Saussure transcrit littéralement les catégories listées dans la coupe phonétique sous forme de tables de symboles et leurs légendes. Pour lui “le système phonologique [est] le tableau des sons qu’il met en oeuvre” (ibid. 1916 [1972 : 58]). Pour obtenir un classement tabulaire à partir d’une description en coupe (conçue comme un instrument de musique résonateur), il met au point une notation faite d’idéogrammes dont l’effectivité combinatoire est, il faut l’avouer, malaisée.
Lecture des tableaux saussuriens
Il faudra donc établir pour chaque phonème : quelle est son articulation buccale, s’il comporte un son laryngé (~~~) ou non ([]), s’il comporte une résonance nasale (. . . .) ou non ([]). Quand l’un de ces trois éléments n’est pas déterminé, l’identification du son est incomplète; mais dès qu’ils sont connus tous les trois, leurs combinaisons diverses déterminent toutes les espèces essentielles d’actes phonatoires.
ibid. 1916 [1972 : 69]
Tableau 1
Tiré de Saussure (1916 [1972 : 72]
Ce premier modèle tabulaire est précis dans ses descriptions des phonèmes, mais ne permet aucune combinatoire.
Structures d’algèbre
La langue est un système serré, et la théorie doit être un système aussi serré que la langue. Là est le point difficile, car ce n’est rien de poser à la suite l’une de l’autre des affirmations, des vues sur la langue; le tout est de le coordonner en système.
Saussure in Godel 1957 : 69
“L’algèbre” dont parle Saussure n’est pas un outil préalable de formalisation, mais se découvre comme une propriété sémiotique de la langue. Ni les méthodes classificatoires et quantitatives, ni la logique déductive, ne constituent des modèles adéquats pour en rendre compte. La linguistique mathématique que réclame Saussure n’est pas une mathématisation ou une formalisation, car, en tant que système sémiotique, la langue est sa propre mathesis. Saussure a recours intuitivement, mais de manière non fortuite, à des structures d’une topologie algébrique qui n’existait qu’à peine en son temps.
De la tabulation idéographique à la numération sémiotique
On peut numéroter les éléments phoniques d’une langue.
– F. de Saussure
Dans l’ontologie négative de Saussure, l’activité de langage ne prend appui que sur des différences et des différences de différences. Ces “rapports de rapports” sont des cas particuliers d’une propriété générale qui s’applique à toute l’architecture du langage.
Dans la langue, il n’y a que des différences. Bien plus : une différence suppose en général des termes positifs entre lesquels elle s’établit; mais dans la langue, il n’y a que des différences sans termes positifs.
1916 [1972 : 166] [nous soulignons.][3]
Devant l’étonnante abstraction de cette déclaration (qu’est-ce qu’une différence sans bornes positives?), il n’est pas étonnant que cette note connue soit restée une belle citation sans suite, faute d’une notation tabulaire numérale pour l’exploiter.[4] Saussure concède que “[…] sans cette fiction, l’esprit se trouverait littéralement incapable de maîtriser une pareille somme de différences, où il n’y a nulle part à aucun moment un point de repère positif et ferme” (2002 : 64-65). Sans cette notation matricielle, la théorie des valeurs pures est inextricable, impraticable et reste enfouie.
Saussure constate que le point de compatibilité entre des numéros, d’une part, et des éléments de langue, d’autre part, est qu’ils sont tous deux porteurs d’une coupure; ce sont des valeurs relatives. Il écrit : “En raison du caractère purement différentiel des éléments phoniques d’une langue, on pourrait se contenter de les désigner par des numéros” (Godel : 69). Sans contradiction, l’usage différentiel des numéros élimine la tentation objective de numéroter quoi que ce soit, car il ne s’agit pas d’assigner des numéros, mais de les appréhender eux-mêmes, dans leur suite disinctive, comme des valeurs. Par cet isomorphisme (numéros/valeurs L), la numération saussurienne opère comme une simulation d’un système différentiel (et non pas comme une formalisation). En d’autres termes, dans la simulation de L, les numéros sont les valeurs.
Au plus simple, les numéros saussuriens sont des nombres ordinaux dont on exploite les propriétés sémiotiques. La structure de données qui porte ces numéros est, par définition, une suite finie; on dit suite, liste ou table (ou tableau) de dimension 1 ou encore paradigme L, selon les usages qui sont très variés. Ces termes sont synonymes pour la propriété sémiotique que nous étudions.
Par le choix exclusif de la différence, Saussure inscrit la pratique grammairienne dans une table numérale qui, par produits cartésiens, établit les dualités de catégories “paires de choses”. Les valeurs (phonèmes) correspondent donc à des jeux de dualités catégoriques.
Un système de dualités solidaires apparaît vite comme une intrication de données qui virent assez tôt à l’amalgame. Saussure note : “Tel qu’il est offert, le langage ne promettrait que l’idée d’une multiplicité, elle-même composée de faits hétérogènes, formant un ensemble inclassable” (2002 : 298). Mais il reste optimiste sur l’analyticité et la systémicité d’un système qui, quoi qu’intriqué, doit pouvoir être construit à partir de “formules relativement simples”. Il écrit :
Le mécanisme de la langue – prise partout À UN MOMENT DONNÉ, ce qui est la seule manière d’en étudier le mécanisme – sera un jour, nous en sommes persuadé, réduit à des formules relativement simples. Pour le moment on ne saurait même songer à établir ces formules.
2002 : 43
Qu’en est-il cent ans plus tard? Saussure ouvre la voie. “Le langage est réductible à cinq ou six DUALITÉS ou paires de choses. – C’est un avantage considérable de pouvoir le réduire à un nombre déterminé de paires” (2002 : 298). Pour être montrable, le système doit être simple. Sans cette minimalité (critère d’évidence), il ne montrerait rien.
Table numérale des catégories phonologiques. Rangs d’aperture A[4]
La phonologie de Saussure surprend par sa numération tabulaire et son mode de classement des données. Il écrit :
On classe généralement les sons d’après le lieu de leur articulation. Notre point de départ sera différent. Quelle que soit la place de l’articulation, elle présente toujours une certaine aperture, c’est-à-dire un certain degré d’ouverture entre deux limites extrêmes qui sont : l’occlusion complète et l’ouverture maximale.
1916 [1972 : 70]
Sur cette base, et en allant de l’aperture minimale à l’aperture maximale, les sons seront classés en sept catégories désignées par les chiffres 0,1,2,3,4,5,6. C’est seulement à l’intérieur de chacune d’elles que nous répartirons les phonèmes en divers types d’après le lieu de leur articulation propre.
1916 [1972 : 70]
Dans le système saussurien, les valeurs phonologiques (qui sont des données diachroniques) sont réparties par rangs d’aperture qui varient entre deux limites extrêmes, une mécanique (occlusion complète), par exemple l’occlusive (p), et une autre dite d’ouverture maximale, par exemple la voyelle lâche (a) au-delà de laquelle la voix peut aller, mais non pas la langue française.
A |
|
1 |
aperture minimale |
2 |
|
3 |
|
4 (5, 6) |
aperture maximale |
Chaque langue se manifeste par le nombre de rangs des apertures qu’elle accepte. Le français, selon Saussure comporte sept rangs qu’une série de tests de minimalisation permet de ramener à six (voire à quatre comme on peut le voir dans le syllabaire).
Tableau 2
Légendes des rangs d’apertures (classement saussurien)
Le graphe des apertures ci-après (qui reproduit un exemple de Saussure) correspond à une image de la chaîne parlée à l’échelle la plus élémentaire. Les points, comme dans un solfège, notent les rangs d’aperture sous lesquels les phonèmes tombent[5] :
particulièrement
Tableau 3
Graphe des apertures
Table des catégories phonologiques
Un des résultats les plus prestigieux de l’École de Prague est d’avoir montré que l’infinie variété des sons de langage dans les six mille langues du monde peut être minimalisée sous un nombre restreint de catégories phonologiques primaires. Les catégories constitutives d’une langue particulière correspondent à un sous-ensemble de cet inventaire. Le système phonologique du français en retient sept données ici, sous une notation traditionnelle :
Tableau 4
Légende des catégories phonologiques du français
Quand on généralise la méthode de numération des rangs d’aperture A (1.2.3.4.5.6) aux autres catégories phonologiques, on obtient la table sous-catégorisée ci-dessous :
Tableau 5
Table des catégories phonologique
Catégorie B, Articulations buccales
De la représentation en coupe phonétique à la tabulation en idéogrammes, jusqu’à la tabulation numérale, la catégorie B (articulations buccales) est sous-catégorisée en huit valeurs, plus une nulle.
Tableau 6
Catégorie B, Articulations buccales
Les cinq catégories VNAAO restantes sont des timbres; elles sont binaires : Voisement (sourd/sonore), Nasalité, Arrondie, Antériorité, Ouverture. On les écrit comme des valeurs booléennes (0,1) permettant ainsi un traitement homogène du système numéral.
Loi de solidarité (S)
Pour l’attestation des valeurs, la phonologie saussurienne requiert un critère plus “serré” que celui qui est en usage dans la phonologie structurale : il s’énonce sous la forme d’une loi de solidarité :
Pour tout phonème appartenant à une langue, il en existe au moins un autre, appartenant à cette langue, identique, à une et une seule différence près.
ΛxєL VyєL / (x = y ± 1 di) |
Loi de Solidarité (loi S) |
Muni de ce critère strict (x = y ± 1 di), l’attestation s’obtient, comme il est d’usage, par commutation ou paires minimales, sachant que les dualités phonologiques n’ont que la distinction du sens pour fonction.
A1 (occlusives et fricatives)
Les formules des valeurs (p | b), bilabiales non-voisée / voisée, sont distinctes à un trait près. Cette distinction est attestée en français comme suit :
Tableau 7
Bilabiales non-voisée / voisée Aperture
En observant la table, on constate que la description de la valeur p est intégralement contenue dans celle de b, car b = p +1 di. Il ne s’agit donc pas de lien (logique) entre des objets, mais d’une “intégration” de valeurs. Cette observation se poursuit dans toute la table.
De même, la valeur b est intégralement contenue dans la valeur m; m = b +1 di. Les deux valeurs sont identiques (ou différentes) ± 1di.
Tableau 8
Bilabiales voisées non-nasales / nasales
Réunissons et comparons les trois valeurs.
Tableau 9
Bilabiables non voisée / voisée/ nasale
Le rang d’aperture et le trait catégorique B (1) (bilabiales) sont communs aux valeurs p b m; le voisement et la nasalité les différencient.
Aperture A2 (liquides)
La même méthode d’attestation stricte à une et une seule différence catégorique près s’applique pour définir l’aperture 2 (liquides) qui ne contient que deux valeurs ( l ) latérale dentale et (r) latérale vibrante.
Tableau 10
Liquides – latérale dentale/latérale vibrante
On peut grasseyer, rouler les (r) ou au contraire les enrouler, cela n’a aucune incidence tant que la différence avec le phonème (l) est maintenue; c’est (r) jusqu’à (l) et vice versa. Saussure souligne cette “latitude dont les sujets jouissent pour la prononciation dans la limite où les sons restent distincts les uns des autres”. (CLG : 164). En d’autres termes, la langue française impose arbitrairement un vide signifiant entre lois et rois; ainsi, une latérale dentale 271 (l), substituée à une vibrante 281(r), peut semer la confusion dans la cité.
l |
nous sommes pour les lois |
latérale dentale |
r |
nous sommes pour les rois |
latérale vibrante |
Aperture A3 semi-consonnes
Les phonèmes A3, appelés semi-consonnes, portent la catégorie B[7].
Tableau 11
Semi-consonnes, Catégorie B
Les couples j - µ et µ - w correspondent à des identités différentielles, à un et un seul trait près. Ainsi les chaînes signifiantes ci-dessus ne se distinguent que par l’occurrence ou l’absence d’une catégorie.
Aperture 4 Voyelles
Dans la table L, un facteur négatif (0) est tout aussi pertinent qu’un facteur positif (1). La catégorie B, par exemple, participe à la formation de toutes les consonnes, semi-consonnes incluses, mais elle est absente des voyelles. Une valeur phonologique qui ne porte pas la catégorie B n’est donc pas une consonne. En conséquence, l’indice de vacuité B (0), par élimination de toutes les consonnes, couvre toutes les voyelles, d’où la règle tabulaire : B (0) → Voyelles.
Aperture 4 voyelles tendues
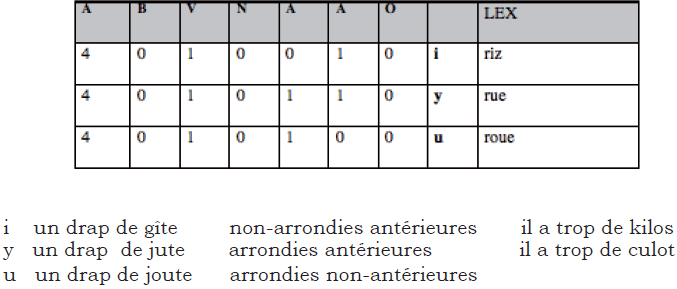
Tableau 12
Aperture 4, Voyelles tendues
La formule des voyelles tendues (i, y, u) est parallèle à celle des semi-consonnes, à la différence près que la catégorie B est nulle.
Aperture 5 voyelles moyennes
Tableau 13a
La différence ouvert|non-ouvert est phonétiquement faible en français, selon les dialectes. Mais l’important ici ne réside pas dans la prononciation, mais dans l’entente (l’attente) d’une différence sémique.
Aperture 5 voyelles moyennes
e |
une tablée d’hôtes |
antérieures |
Ə |
une table d’hôtes |
non-antérieures |
Dans le premier cas, il s’agit d’invités; dans le second, il s’agit de clients.
Résumons la table :
Tableau 14
Table des valeurs phonologiques (phonèmes) du français
La déconstruction, par paires minimales, des valeurs phonologiques du français constitue une attestation empirique rigoureuse, car il ne suffit pas de dire que tout dans la langue est différence, il faut ajouter que ces différences sont établies à un trait près et qu’elles forment un système clos. Ainsi, l’écriture tabulaire numérale garantit l’analyticité de la théorie, mais aussi sa systémicité. Appliquons la loi pour montrer sa systémicité, appliquons la loi de Solidarité[8].
Voisinages topiques
Une valeur “vaut”, à une di (différence) près, toutes les valeurs qu’elle n’est pas; ce jeu de valeurs défectives constitue son voisinage topique. Le graphe ci-dessous montre que le phonème o, est identique, à un et un seul trait près, à tous les phonèmes qui constituent son voisinage.
Voisinage topique de la voyelle o
Tableau 15
Voisinage de la voyelle (o)
Dans un voisinage topique, toute valeur est la transformée d’une autre, au moins. Autrement dit, chaque phonème est une valeur “pure”, “entité négative”, sans soma ni “substance”, uniquement définie par sa différence avec d’autres valeurs, à un et un seul trait différentiel près. Le schéma ci-dessus suggère une analogie avec la musique : “Les phonèmes ne sont pas des notes isolées, mais des accords composés de plusieurs éléments” (B. de Courtenay 1910; in Jakobson & Waugh 1979 : 28).
Topiques de phonèmes : système phonologique
En appliquant la loi S dans la table des valeurs, on établit le voisinage de chaque phonème et, dès lors, sa définition minimale. Cette méthode descriptive est précieuse, mais reste manuelle. En poussant plus avant, les dérivations aboutissent, par principe de clôture, à la définition de quatre espaces phonologiques, appelés topiques de phonèmes, espaces sémiotiques clos qui correspondent aux quatre rangs d’aperture A (1.2.3.4).
Tableau 16
Topique des consonnes A1
Dans le graphe ci-dessous, chaque ligne entre deux indices correspond à une différence catégorique, une et une seule (±1 di). Commençons par un graphe aveugle sans légendes pour montrer l’effectivité de la simulation du système phonologique par numération et son autonomie algorithmique.
Tableau 17
Graphe aveugle
Le graphe sans légende montre la clôture algébrique des valeurs d’aperture A1 et le réseau de leur maintien mutuel, à un trait près. Effectuons une boucle. Les formules qui décrivent les phonèmes 310 et 210 sont identiques à 1 trait près. Plus avant, 210 est identique à 211, à 1 trait près. 211 est identique à 311, à 1 trait près et, en fin de boucle, 311 est identique, à 1 trait près, à 310 donnée au départ. Au graphe ci-dessous, identique au précédent, sont ajoutées des légendes qui permettent d’effectuer des tests interprétés.
Tableau 18
Graphe légendé, Topique des consonnes d’Aperture 1
Effectuons de nouveau une boucle. Le phonème g est identique à k à un trait près, k est identique à t à un trait près, t est identique à d à un trait près, d est identique à g, à un trait près, donné au départ. Autrement dit, la valeur g est identique à elle-même via sa différence avec toutes les autres.
Tableau 19
Boucles d’identification de consonnes (x = y ± 1di)
Ainsi, la topique des consonnes constitue un exemple d’espace de solidarité autonome dans l’architecture de la grammaire.
Topique des voyelles
Le domaine des voyelles du français est réparti sur les trois rangs d’aperture A (4, 5, 6) et forme un système fermé pour la définition de ses valeurs.
Les voyelles forment, elles aussi, un tout solidaire, un système fermé sous une loi. A toute voyelle correspond une voisine, au moins, répondant à la règle (x = y ±1). En d’autres termes, l’identification d’un phonème (x = x) transite par la boucle de ses transformés possibles.
[Ø] = [o] = [ ] = [e] = [Ø] parcours d’identification (x = x) ± 1di
[Ø]= [y=] [u=] [o=] = [Ø]
À toute valeur correspond, au moins, un parcours différentiel en boucle qui la définit. Il suffit de pointer un indice numérique correspondant à une voyelle et chercher dans la topique sa définition dans un autre (à un trait de différence), puis un autre et, ainsi de suite jusqu’au retour à l’indice d’origine.
Tableau 20
Topique des Voyelles
Dans le graphe, chaque ligne reliant deux valeurs représente une différence catégorique (± 1di). On obtient l’identification d’une valeur (x = x) par la réitération de l’opération ± 1di sur ses propres résultats. En voici le schéma déroulé.
Tableau 21
Schéma déroulé
L’identification d’une valeur avec elle-même transite par ses différences avec toutes les autres. Ainsi, l’identité et la différence sont coextensives (id ≅ di) pour toute valeur. D’un phonème à l’autre, nous sommes dans du même, car la description d’un phonème est inscrite, à une différence près, dans la description d’un autre, au moins. Ainsi, les phonèmes, valeurs paradigmatiques, communiquent entre eux par “intégration” et non par lien logique. Entre deux phonèmes voisins, il y a une différence discrète (qualitative), mais il n’y a ni rupture ni de suture. Un phonème attesté n’est donc pas un objet, mais une configuration négative de voisinages (± 1 di) en effectivité constante.
Sous chaque phonème pointé opère une topique de valeurs, présente et silencieuse. Cet espace sémiotique est formellement clos; autrement dit, c’est un holisme local, un système autonome (immanent), une monade. Les parcours en boucles d’identification suppriment la nécessité d’une référence externe. Saussure pose le problème en ces termes : “La langue ne s’alimente dans son essence que d’oppositions, d’un ensemble de valeurs parfaitement négatives et n’existant que par leur contraste mutuel” (Saussure 2002 : 40). Benveniste souligne plus tard : “Les entités linguistiques ne se laissent déterminer qu’à l’intérieur du système qui les organise et les domine, et les unes par rapport aux autres. Elles valent qu’en tant qu’éléments d’une structure” (Benveniste 1966 : 151).
Les valeurs ne se transportent pas en dehors du système dont elles émanent, système qui s’effondre si l’une d’entre elles vient à faillir; c’est ce que “solidarité”, “pertinence”, et, à terme, prédictibilité, veulent dire.
Conclusion
Le phonème est un objet synchronique très fin. Les grands linguistes qui l’ont découvert, Baudouin de Courtenay, Kruszewski jusqu’à Ferdinand de Saussure et l’École de Prague, ont fondé, par cette découverte, la linguistique théorique (linguistique générale moderne). Mais comme le montre la mise au jour des topiques de phonèmes, espaces sémiotiques fermés, le statut de cet objet défectif mérite d’être encore approfondi. Quand bien même Saussure n’a souvent qu’esquissé ses analyses, il a construit, une programmatique,très solide qui suffit de suivre comme nous l’avons fait. Certes, il n’est pas allé au delà des techniques et méthodes qui permettent d’établir des tables de valeurs. Sans doute, comme le souligne Utaker (2002), il “n’en avait-il pas les moyens”. Toutefois sa conception d’un “système fermé” (Saussure 2002 : 139) témoigne de son intention d’y parvenir.
Parties annexes
Note biographique
JACQUES COURSIL est Professeur émérite en Sciences du langage, Docteur en linguistique ainsi que Docteur en informatique formelle (Intelligence Artificielle). Parmi les articles qu’il a consacré à F. de Saussure, on trouve : “La phonologie de Saussure (deux théorèmes)”; “Le Syllabaire Saussurien”; “Architecture de la signification”; “Charles Bally et le programme de Saussure”; et “Dualités intégrées, le maître-argument saussurien”. Il est également l’auteur de La fonction muette du langage : essai de linguistique générale contemporaine (Ibis Rouge 2000) et de Valeurs Pures, Le programme systémique de Ferdinand de Saussure (Lambert-Lucas 2015).
Notes
-
[1]
En son temps, Saussure avait la double tâche de décrire diachroniquement et synchroniquement les catégories phonologiques des langues. Aujourd’hui, pour une langue comme le français, ces catégories ne sont plus à découvrir. Un siècle de travaux nous laisse des descriptions rigoureuses et somme toute, l’embarras du choix. Pour en bâtir le système, car c’est de cela seul dont il s’agit, nous emprunterons comme hypothèses de travail, des listes de catégories déjà élaborées dont la fiabilité descriptive est avérée. Notre tâche systémique se trouve simplifiée puisque nous disposons de données fiables sans avoir eu, comme le maître genevois, à les construire préalablement.
-
[2]
Dans sa description phonétique, Saussure comme la plupart des phonologues, considère les phonèmes comme des sons, mais en même temps, comme des empreintes psychiques. Dans son programme phonologique, ce sont des entités négatives, des valeurs pures, des vides, des kénomes, des entités distinctives, oppositives et relationnelles. Toutes ces propriétés caractéristiques renvoient à leur négativité. La phonologie est autonome. Les phonèmes ne sont pas phonétiques; ce sont des formes sans substance, sans matérialité. Le son de langage n’apparaît que de leurs oppositions dans les résonnances de la syllabe. Ainsi, les consonnes qui sont des phonèmes ne sont pas prononçables sans le soutien d’une voyelle avec laquelle elles forment une syllabe.
-
[3]
De manière formelle, la table, structure de données de bas niveau (le plus bas), est considérée comme la matrice de toutes les écritures. Dans son étude sur l’Ars Combinatoria de Leibniz, le mathématicien philosophe M. Serres (1969) écrit : “Nulle discipline mathématique n’échappe à la juridiction tabulaire”.
-
[4]
Les apertures saussuriennes correspondent aux rangs de laxité ou tension, dans le vocabulaire de Jakobson.
-
[5]
Ce graphe peut être trompeur quand on associe les notions de rangs de tension phonologique à des rangs de fréquences. Les deux graphes ci-dessous, respectivement, tension vs fréquences, montrent que le parallèle est rompu; dans le triplet (u, o, a), la voyelle (u) est la plus tendue et en même temps, à l’inverse, la plus grave.

-
[6]
Saussure écrit : “Nous nous conformerons à la terminologie courante, bien qu’elle soit imparfaite ou incorrecte sur plusieurs points: des termes tels que gutturales, palatales, dentales, liquides etc. sont tous plus ou moins illogiques.... La dénomination “gutturales” est non seulement arbitraire, mais fausse; on arriverait à des noms grotesques “cérébrales!” (1916 [1972 : 70]). Dans une écriture tabulaire numérale, les mots employés pour désigner les catégories sont indifférents. Ces noms, avatars plus qu'héritage de la tradition phonétique, ne sont ici que des légendes pour des indices numériques qui seuls comptent dans la définition des valeurs. Toutefois, sans ces légendes, l’analyste serait vite débordé(e) dans des labyrinthes chiffrés.
-
[7]
Les semi-consonnes sont souvent appelées semi-voyelles parce qu’elles intègrent dans leur définition des catégories propres aux voyelles : A, Arrondie et A, Antérieure.
-
[8]
La fonction des phonèmes comme différentiateurs sémantiques relègue hors champ les méthodes quantitatives. Pour Saussure, comme pour Troubetzkoy plus tard, “la langue est en dehors de la mesure et du nombre”.
Bibliographie
- ARISTOTE (1962). Seconds analytiques. J. Tricot (Trad.). Paris : Vrin.
- BALLY, Ch. (1913) Le langage et la vie. Genève : Atar.
- BENVENISTE, E. (1966) Problèmes de linguistique générale, I. Paris : Gallimard.
- BENVENISTE, E. (1974) Problèmes de linguistique générale, II. Paris : Gallimard.
- BERGOUNIOUX, G. (2010) “La phonologie comme morphologie”. Le Projet de Ferdinand de Saussure, J.-P. Bronckart, É. Bulea & C. Bota (Éds.). Genève : Droz.
- BERTALANFY, L. (1982) Des robots, des esprits et des hommes. Chouraqui-Sepel (Trad). Paris : ESF.
- BÜLHER, K. (1931) “Phonetik und phonologie”. In Travaux du Cercle linguistique de Prague (4) : 22–53.
- COURSIL, J. (1995) “Analytiques de la pholologie saussurienne : deux théorèmes”. In Saussure aujourd’hui. Arrivé M. et Normand Cl. (Éds.), Nanterre, In LINX, N° spécial : 323-352.
- COURSIL, J. (2000) La fonction muette du langage. Pointe à Pitre : Ibis Rouge.
- COURSIL, J. (2015) Valeurs pures, le programme systémique de Ferdinand de Saussure. Limoges : Lambert-Lucas.
- GODEL, R. (1957) Les sources manuscrites du Cours de Linguistique Générale de Ferdinand de Saussure. Genève : Droz
- HJELMSLEV, L. (1968) Prolégomènes à une théorie du langage. Paris : Minuit.
- JAKOBSON, R. (1976) Six leçons sur le son et le sens. Paris : Minuit.
- JAKOBSON, R. & WAUGH, L. (1979) The Sound Shape of Language. Hassocks : Harvester.
- KLEENE, S. C. (1965) The Foundations of Intuitionistic Mathematics. Amsterdam : North-Holland.
- KUHN, T. ( 1983) La structure des révolutions scientifiques. Paris : Flammarion.
- von LEIBNITZ, G. W. (1978) La monadologie. Paris : Delagrave.
- LE MOIGNE, J.-L. (1999) Epistémologies constructivistes. Paris : PUF.
- MILNER, J-C. (1989) Introduction à la science du langage. Paris : Seuil.
- NEF, F. (2000) Leibniz et le Langage. Paris : PUF.
- PARRET, H. (1993) “Les manuscrits saussuriens de Harvard”. In Cahiers Ferdinand de Saussure (47) : 179-234.
- SAUSSURE, F. de (1916 [1972]) Cours de linguistique générale. Publié par Ch. Bally & A. Sechehaye avec la collaboration de A. Riedlinger. Édition critique préparée par Tullio De Mauro. Paris : Payot.
- SAUSSURE, F. de (1968-1974) Cours de linguistique générale. Édition critique par R. Engler. [4 fascicules en deux volumes] Wiesbaden : Harrassowitz.
- SAUSSURE, F. de (2002) Écrits de linguistique générale. Paris : Gallimard.
- SERRES, M. ( 1968) Le système de Leibniz et ses modèles mathématiques, t. I et II. Paris : PUF.
- TROUBETZKOY, N. (1949) Principes de phonologie. J. Catineau (Trad). Paris : Klincksieck.
- UTAKER, A. (2002) La philosophie du langage. Une archéologie saussurienne. Paris : PUF.
Liste des figures
Liste des tableaux
Tableau 1
Tiré de Saussure (1916 [1972 : 72]
Tableau 2
Légendes des rangs d’apertures (classement saussurien)
Tableau 3
Graphe des apertures
Tableau 4
Légende des catégories phonologiques du français
Tableau 5
Table des catégories phonologique
Tableau 6
Catégorie B, Articulations buccales
Tableau 7
Bilabiales non-voisée / voisée Aperture
Tableau 8
Bilabiales voisées non-nasales / nasales
Tableau 9
Bilabiables non voisée / voisée/ nasale
Tableau 10
Liquides – latérale dentale/latérale vibrante
Tableau 11
Semi-consonnes, Catégorie B
Tableau 12
Aperture 4, Voyelles tendues
Tableau 13a
Tableau 14
Table des valeurs phonologiques (phonèmes) du français
Tableau 15
Voisinage de la voyelle (o)
Tableau 16
Tableau 17
Graphe aveugle
Tableau 18
Graphe légendé, Topique des consonnes d’Aperture 1
Tableau 19
Boucles d’identification de consonnes (x = y ± 1di)
Tableau 20
Topique des Voyelles
Tableau 21
Schéma déroulé



![Tiré de Saussure (1916 [1972 : 72]](/fr/revues/rssi/2014-v34-n1-2-3-rssi02602/1037147ar/media/1987441n.jpg)