Abstracts
Résumé
La décision psychométrique qui consiste à décréter qu’un candidat, évalué par un test et dont le score est confronté à une norme, « passe » ou « ne passe pas » fait face à deux incertitudes, deux sources d’erreur : l’erreur de mesure, reflétée par le coefficient de fidélité du test et modifiant peu ou prou la valeur vraie du candidat, et la variabilité échantillonnale de la norme, celle-ci étant ordinairement basée sur un échantillon et présentant sa propre distribution d’erreur. À la suite de l’examen de l’incertitude de la norme et de son contrôle (Laurencelle, 2015), nous abordons ici l’erreur de mesure et son interaction avec l’incertitude de la norme, puis nous intégrons les deux dans un système mathématique basé principalement sur la loi normale. La probabilité que soit sélectionné un candidat non méritant ou non qualifié peut être calculée, tout comme celle qu’un candidat qualifié soit rejeté. Nous proposons enfin le concept et la méthodologie de la « norme sûre » (Laurencelle, 2002), laquelle permet de contrôler statistiquement le risque d’une erreur de décision.
Mots-clés :
- décision psychométrique,
- erreur de mesure,
- incertitude de la norme,
- norme sûre
Abstract
Test-based ruling, i.e. deciding whether an examinee whose test score is compared to some norm or threshold « passes » or « passes not », must cope with two uncertainties, two error sources: measurement error, associated with the test’s reliability index and corrupting somewhat the individual’s true score, and the sampling variability of the norm, a value generally based on a sample and slurred by its own error distribution. Following our study of the norm’s statistical properties and their control (Laurencelle, 2015), we now tackle measurement error and its interaction with the norm’s uncertainty, incorporating both in a mathematical system based generally on the normal distribution. The odds that an unqualified candidate be retained may be calculated, as may those of a qualified one be rejected. Finally, we propound the concept and methodology of the «safe norm » (Laurencelle, 2002), a device that makes possible to statistically control the risk of a decision error.
Keywords:
- test-based ruling,
- measurement error,
- norm’s uncertainty,
- safe norm
Resumo
A decisão psicométrica de declarar que um candidato, avaliado por um teste e cujo resultado é confrontado com uma norma, «passa» ou «não passa» enfrenta duas incertezas, duas fontes de erro: o erro medição, reflectido pelo coeficiente de fidelidade do teste e pela alteração mais ou menos do valor verdadeiro do candidato, e a variabilidade de amostragem da norma, geralmente baseada numa amostra e apresentando a sua própria distribuição de erro. Após análise da incerteza da norma e do seu controlo (Laurencelle, 2015), discutimos aqui o erro de medição e a sua interação com a incerteza da norma, integrando os dois num sistema matemático com base principalmente na distribuição normal. A probabilidade de ser selecionado um candidato sem mérito ou não qualificado pode ser calculada, assim como a probabilidade de um candidato qualificado ser rejeitado. Finalmente, propõe-se o conceito e a metodologia da «norma segura» (Laurencelle, 2002), a qual permite controlar estatisticamente o risco de um erro de decisão.
Palavras chaves:
- decisão psicométrica,
- erro de medição,
- incerteza da norma,
- norma segura
Article body
Introduction
Un usage signalé des tests psychométriques consiste à enregistrer le résultat obtenu par un candidat, puis à baser une décision sur celui-là, tel qu’on le fait pour la sélection du personnel, la mutation d’un employé d’un poste à un autre dans une grande organisation, la qualification d’un candidat pour l’inscription à un programme d’études ou l’enrôlement d’un joueur dans une équipe sportive. Cette décision psychométrique, qui par ailleurs doit s’appuyer sur divers éléments du contexte d’évaluation (voir p. ex. Pettersen, 2000), dépend essentiellement d’une confrontation entre le score obtenu par le candidat et une norme (ou, à l’occasion, quelques normes) établie pour le test. La norme, ou seuil de réussite, consiste habituellement en un centile formé à partir d’une banque de données issues d’un groupe de référence, l’échantillon normatif. Dans la Partie I de cet essai (Laurencelle, 2015), nous avons montré que la norme, baptisée CP, est en fait une statistique et qu’en conséquence elle possède un caractère aléatoire grâce auquel le taux de sélection prescrit n’est pas généralement respecté. Nous explorons ici l’autre terme de la décision psychométrique, soit l’instabilité du score due à l’ingrédient aléatoire qu’il comporte, puis son interaction avec l’incertitude échantillonnale du seuil CP. Enfin, nous proposons une « norme sûre » grâce à laquelle le décideur sera à même de contrôler en probabilité le risque d’une mauvaise décision.
Avant d’aborder les trois volets de cet essai, rappelons d’abord quelques conventions de vocabulaire et de notation. Soit une population donnée, de taille N pratiquement infinie ; le sous-ensemble de personnes méritantes pour la sélection, de taille NK, détermine le taux de sélection appliqué, soit K = NK / N ; ce taux nominal K est souvent prescrit. Dans la distribution des scores X de la population, la personne tout juste méritante occupe le rang centile P, où P = 1 – K (sur une échelle de 0 à 1), correspondant au centile XP. Dans le cas idéal d’un score X pur (c.-à-d. mesuré sans erreur) et d’un centile XP déterminé sur la population entière, la décision de retenir le candidat si X ≥ XP ou de le rejeter si X < XP sera correcte avec probabilité 1. Le taux de sélection K est aussi désigné taux de capture.[1]
Les cas réels, toutefois, diffèrent de deux façons du cas idéal évoqué ci-dessus. En premier lieu, la mesure X d’une personne, produite par l’application d’un procédé de mesure, d’un test, d’un procédé d’évaluation, est imprécise et elle fluctue ordinairement d’une fois à l’autre en raison d’une composante aléatoire, appelée « erreur de mesure » en théorie des tests (Gulliksen, 1950 ; Lord & Novick, 1968 ; Laurencelle, 1998 ; Bertrand & Blais, 2004). Cette variation aléatoire des scores du test pour la même personne est reflétée à la fois par le coefficient de fidélité R (ou rXX), variant de 0 à 1, et par l’erreur-type de mesure se. En second lieu, la norme, c.-à-d. le seuil centile utilisé pour confronter la mesure X, est généralement basée sur un échantillon normatif de taille n, non pas sur les N éléments de la population, où n est si petite par rapport à N que le ratio n / N tend vers 0. Dans ce cas, la norme estimée, CP, peut et va s’éloigner en plus ou en moins de la norme réelle XP, puisqu’elle-même a sa distribution d’erreur telle qu’elle est documentée dans la Partie I de l’essai. Dans un contexte d’application général, les deux sources d’erreur jouent conjointement de sorte que, en pratique, l’évaluateur-décideur devra comparer un score X à valeur imprécise à un seuil centile plus ou moins décalé par rapport à la norme correcte qui est prescrite. Par rapport au taux de capture convenu K, le taux de capture réel, disons k, sera donc fonction de la taille n et de la fidélité R. Il dépendra aussi de la conformité du modèle de distribution observé par rapport au modèle stipulé.
Rappelons d’entrée de jeu que, dans le modèle de la théorie des tests, le score X, de moyenne µX et variance σ2x , est composé additivement d’un « score vrai » V, caractéristique de la personne mesurée, et d’une « erreur » aléatoire e, selon l’équation X = V + e, les scores vrais ayant pour moyenne µV = µX et pour variance σ2v = R·σ2x , et les erreurs, µe = 0 et σ2e = (1 – R) σ2x . En valeurs standardisées, il est d’usage d’employer µX = µV = µe = 0, σ2x = 1, σ2v = R, σ2e = 1 – R ; c’est sous cette forme standardisée que nous présentons les développements suivants.
L’erreur de mesure et sa distribution
D’après le modèle classique Xi,o = Vi + eo dans lequel i et o dénotent respectivement l’individu évalué et l’occasion de mesure, l’erreur de mesure e associée à chaque mesure X se voit typiquement et vraisemblablement attribuer la forme de distribution normale, de paramètres µe = 0 et σe2 = (1 – R) σ2x , forme notée succinctement e ~ N(0; 1 – R) dans sa forme standard. D’autres modèles de distribution ont aussi été explorés (Lord & Novick, 1968), notamment le modèle binomial.
La mesure X confrontée à une norme stable
Bien que le cas soit rare, il est possible d’obtenir une norme stable basée soit sur l’ensemble de la population N, soit sur une fraction majeure de celle-ci (selon n / N → 1). Dans ce cas, le psychométricien dispose directement de XP, le centile juste séparant les plus forts 100 · K (= 1 – P) % de la population. Or, la prescription d’un taux de sélection K signifie qu’on veut, par ce moyen, repérer les éléments qui présentent les meilleures valeurs vraies de la population, nonobstant l’erreur de mesure qui est attachée à ces valeurs. Considérant que les scores X de la population de référence sont tous et individuellement marqués d’une composante e, la règle de sélection envisagée, soit « Sélectionner i si Xi ≥ XP », devient, lorsque traduite honnêtement en valeurs vraies :
Aussi, parce qu’elle est mitigée par une composante aléatoire e, la valeur X obtenue près de XP a pu devoir sa position avantageuse à l’addition de e. Par exemple, la valeur Xi,o = Vi + eo > XP peut avoir été produite par un candidat pour qui Vi < VP, à condition que eo > XP – VP. Afin de contrôler et de réduire ce risque de sélection inappropriée, il faut préventivement décaler le seuil appliqué CP au-delà du seuil de sélection théorique XP.
La détermination du critère de sélection peut aussi être envisagée a contrario, en partant d’une valeur « contaminée » X* proche du seuil de sélection naïf XP, et en lui associant la valeur V* qui lui est corrélée, sa concomitante (David, 1981). Posant que la corrélation entre valeurs observées et valeurs vraies est ![]() , nous obtenons, en valeurs standardisées :
, nous obtenons, en valeurs standardisées :
et :
selon les équations 5.7.3 de David (1981, p. 110). Il est intéressant de noter aussi que, pour R < 1, les indices de forme γ1 et γ2 de la variable V* sont raisonnablement proches de 0, de sorte que le modèle normal utilisant les paramètres de moyenne (2) et de variance (3) convient à peu près pour V*.
En posant X* = XP, nous obtenons E(V*) = R · E(XP), une valeur plus basse que celle (1) trouvée par l’approche précédente : l’écart est de (![]() – R) × σX, maximal lorsque R = 0,25. L’utilisation naïve du seuil X* = XP, dans le but de retenir la meilleure portion K = 1 – P de la population, aboutirait ainsi à garder en moyenne une portion égale à K* – K > 0 de candidats non qualifiés[2]. La raison en est que, dans l’obtention d’un score X ≥ X*, la valeur vraie V contribue certes, mais aussi la composante e, laquelle vient ainsi décaler en plus ou en moins la relation entre X et V. Une solution pour contrecarrer le biais résultant consisterait à prescrire un seuil X* = XP /
– R) × σX, maximal lorsque R = 0,25. L’utilisation naïve du seuil X* = XP, dans le but de retenir la meilleure portion K = 1 – P de la population, aboutirait ainsi à garder en moyenne une portion égale à K* – K > 0 de candidats non qualifiés[2]. La raison en est que, dans l’obtention d’un score X ≥ X*, la valeur vraie V contribue certes, mais aussi la composante e, laquelle vient ainsi décaler en plus ou en moins la relation entre X et V. Une solution pour contrecarrer le biais résultant consisterait à prescrire un seuil X* = XP / ![]() , entraînant l’espérance E(V*) = R × X* =
, entraînant l’espérance E(V*) = R × X* = ![]() XP, comme il se doit. Pour des raisons de clarté et de facilité de distribution, nous retiendrons la première approche.
XP, comme il se doit. Pour des raisons de clarté et de facilité de distribution, nous retiendrons la première approche.
La figure 1 montre une situation dans laquelle la sélection chercherait les 100 · K = 5 % (P = 0,95) meilleurs candidats dans la population, le score X ayant une fidélité R = 0,80. La répartition de la population, en valeurs standardisées, est indiquée (partiellement) par la ligne pointillée. Le score de césure servant à démarquer les 5 % supérieurs est ici XP = X0,95 ≈ 1,645, et la valeur vraie identifiant le candidat tout juste qualifié est ![]() . Le candidat représenté obtient (théoriquement) V = 1,20 et n’est donc pas qualifié ; il ne devrait pas être retenu. Or, son score mesuré, X = V + e = 1,20 + e, varie en fonction de e, comme le montre la distribution normale en ligne pleine. Ce score peut ainsi, au hasard, être amené au-delà du seuil XP, dans la zone A du graphique : un petit calcul[3] indique que la probabilité de sélection indue est ici de 0,160.
. Le candidat représenté obtient (théoriquement) V = 1,20 et n’est donc pas qualifié ; il ne devrait pas être retenu. Or, son score mesuré, X = V + e = 1,20 + e, varie en fonction de e, comme le montre la distribution normale en ligne pleine. Ce score peut ainsi, au hasard, être amené au-delà du seuil XP, dans la zone A du graphique : un petit calcul[3] indique que la probabilité de sélection indue est ici de 0,160.
Figure 1
Illustration de l’impact de l’erreur de mesure e sur la sélection selon le critère X = V + e ≥ XP (norme XP selon n → ∞). Le candidat considéré aurait la valeur V = 1,20. La ligne pointillée marquée 𝑓(X) représente la répartition de la population
Étant donné que, d’une part, la « valeur » du candidat repose d’abord sur sa valeur vraie V, donc sur sa position relative par rapport au seuil VP, et que, d’autre part, la valeur V n’est pas directement mesurable, il faut plutôt relever le seuil de sélection CP au-delà de XP dans le but raisonnable de contrôler le risque d’une sélection insatisfaisante, c.-à-d. garder la probabilité d’une telle sélection sous un seuil donné α, etce, pour tout candidat n’atteignant pas le seuil VP. Dans le présent contexte, la détermination du seuil CP s’obtient, en valeurs standardisées, par :
En posant α = 0,05, nous obtenons une valeur établie pour CP de 2,207. Pour notre ami théorique situé à V = 1,20, sa probabilité d’être retenu en vertu de ce seuil tombe alors à 0,012.
Il est intéressant aussi de considérer le cas d’un candidat qualifié. Reprenant le contexte ci-dessus, où le seuil de qualification était VP ≈ 1,471 et le seuil de sélection brut, XP ≈ 1,645, posons un candidat à valeur vraie V = 1,60, soit une valeur un peu au-dessus du seuil VP. Le jeu de l’erreur de mesure e influera ici aussi sur la probabilité de sélection, le calcul donnant une valeur de 0,613 et la probabilité de non-sélection (erronée) étant complémentairement 0,387. Si maintenant nous instaurons la protection invoquée plus haut et destinée à borner à α = 0,05 la probabilité d’une mauvaise sélection pour les candidats non qualifiés, le seuil applicable est de 2,207 au lieu de 1,645, et la probabilité de retenir notre individu qualifié descend à 0,087.
Examinons maintenant le cas général dans lequel l’erreur de mesure et l’incertitude positionnelle du seuil CP jouent concurremment dans la décision normative ainsi que leur impact conjoint sur le taux de sélection.
Incertitude du seuil CP + erreur de mesure sur le score X
Pour récapituler, tous contextes normatifs, en particulier ceux relatifs à la sélection comme au classement des candidats, reposent sur quelques paramètres fondamentaux, les deux premiers étant la taille du groupe normatif n et le taux de sélection K ou 1 – P. La norme elle-même, notée CP, est établie sur la base d’un échantillon normatif de taille n. Que cette norme soit calculée par un décalage linéaire λ (p. ex., CP = X̅ + λP,n · sX) ou trouvée dans une statistique d’ordre X(r) (p. ex., CP = X̅ (r = 𝑓 (P, n)) ; voir Laurencelle, 2015), elle est imprécise, devant son incertitude à l’échantillon qui a servi à l’établir, et elle contribue ainsi au risque de sélection erronée.
À ce contexte, sera confronté un candidat obtenant le score X, un score lui-même imprécis en raison d’une fidélité (ordinairement) imparfaite R, ce coefficient étant un troisième paramètre à considérer dans la décision normative. Lorsque R < 1, le score X individuel comporte en effet, comme nous venons de l’illustrer, une partie aléatoire e qui dérange la position réelle V du candidat, de sorte qu’il y a derechef risque de sélection erronée pour cette nouvelle raison.
Les deux sources d’incertitude sont indépendantes l’une de l’autre. L’incertitude positionnelle du seuil CP caractérise l’appareil normatif établi et reste la même pour tout candidat qui lui est confronté. Quant à l’erreur de mesure e affectant le score X (= V + e) individuel, elle est renouvelée à chaque mesure. C’est le traitement conjoint de ces deux sources, soit explicitement l’intersection des distributions des variables aléatoires correspondantes, qui permet de mesurer le risque global de sélection erronée et, éventuellement, de le contrôler.
Globalement, nous cherchons à déterminer la probabilité qu’un candidat à valeur vraie V* soit retenu pour sélection selon que sa mesure effective, soit V* + e, déborde CP. Cet énoncé, exprimé symboliquement « P = Pr {V* + e ≥ CP} », peut, en posant la norme CP comme variable, se réécrire symboliquement :
pour une valeur e donnée et, en général,
pour l’ensemble des valeurs e possibles, où 𝑓e(e) dénote la densité de l’erreur e. Posant
comme fonction de répartition de la norme CP, nous pouvons finalement réécrire (6) sous la forme :
Telle est la forme générique du calcul de la probabilité qu’un candidat à valeur vraie V* déborde la norme empirique CP, sous l’influence de l’erreur de mesure e.
Examinons maintenant la réalisation de ce calcul d’abord pour la norme linéaire normale, puis pour la norme ordinale normale.
Norme linéaire normale
En valeurs standardisées, la norme linéaire, définie par une fonction de la moyenne et de l’écart-type de la série normative, soit :
a pour densité[4] (Laurencelle, 2015, équation 7) :
correspondant aussi à la loi du t non-central (Johnson, Kotz & Balakrishnan, 1995, chap. 31) : gs et hX̅ indiquent respectivement la densité de l’écart-type normal, de loi ![]() , et de la moyenne normale, de loi N(0; 1 / n). Le paramètre clé de cette norme, λ, permet de contrôler la probabilité (8) et sert donc de référence pour le système normatif à établir.
, et de la moyenne normale, de loi N(0; 1 / n). Le paramètre clé de cette norme, λ, permet de contrôler la probabilité (8) et sert donc de référence pour le système normatif à établir.
La figure 2 reprend l’exemple donné à la figure précédente, cette fois en confrontant le score contaminé X = V + e, V = 1,20, à une norme empirique CP basée sur un échantillon de n = 200 données normales, norme naïvement ancrée dans le centile 95, ici λ = Φ–1 (0,95) ≈ 1,645. L’aire A, intégrée comme en (8) sous le tracé foncé, donne ici une probabilité de sélection de 0,168 pour ce candidat non qualifié, comparativement à 0,160 lorsqu’il était confronté à une norme stable, soit XP = 1,645 ; le risque de mauvaise sélection est donc légèrement accru. Pour l’autre candidat (non illustré sur la figure 2), celui qualifié à valeur vraie V = 1,60 (débordant le seuil de qualification VP ≈ 1,471), sa probabilité de sélection, qui était de 0,613 contre la norme XP, diminue à 0,463 sous la norme fluctuante CP.
Figure 2
Illustration de l’impact de l’erreur de mesure e sur la sélection selon le critère X = V + e ≥ CP (norme CP selon n = 200)
Norme ordinale normale
À la norme linéaire présentée ci-dessus, nous pouvons juxtaposer une norme ordinale, ou centile ordinal normalisé, CP = X(r), r ~ 𝑓 (P, n), qui n’exploite de la distribution normative que les propriétés locales normales des centiles, c.-à-d. des statistiques d’ordre {X(1), X(2), …, X(n)} de la série normative, sans recourir aux indices globaux de moyenne et d’écart-type. Pour une variable X de loi normale standard, la densité de cette norme X(r) est (Laurencelle, 2015, équation 15) :
et sa fonction de répartition (David, 1981) est :
Quant à nos deux candidats, s’ils sont confrontés à la norme ordinale correspondant à P = 0,95, soit X(r) où r = P × (n + 1) = 0,95 × 201 ≈ 191, le calcul d’après l’équation (8) montre que le premier (avec V = 1,20) serait faussement retenu à probabilité de 0,162, et le second (avec V = 1,60), correctement sélectionné à probabilité de 0,445.
Les données présentées à la figure 3 illustrent l’impact de différents niveaux de l’erreur de mesure, le graphique exhibant cette fois la probabilité d’être sélectionné pour tout candidat qualifié, c.-à-d. une personne possédant un score V dans la zone allant de VP à l’infini. Comme le montre la figure, la forme de la courbe de probabilité, forme qui varie selon le degré de fidélité R, donne lieu à trois constatations. Primo, l’origine de la courbe, VP, augmente avec R, allant ici de V0,95 = X0,95 × ![]() ≈ 1,645 ×
≈ 1,645 × ![]() ≈ 1,471 pour R = 0,80 jusqu’à X0,95 ≈ 1,645 pour R = 1. Secundo, la montée de la courbe se fait plus abrupte, plus discriminante : cette montée serait tout à fait verticale pour une taille n → ∞ et séparerait exactement les candidats qualifiés et non qualifiés. Enfin, tertio, une quasi-certitude de sélection est atteinte plus rapidement pour une fidélité élevée. L’utilisation d’autres valeurs paramétriques de taille (n), de taux de sélection (1–P), voire de mode de détermination de la norme (linéaire, ordinale) donne lieu à des comparaisons et à des conclusions semblables.
≈ 1,471 pour R = 0,80 jusqu’à X0,95 ≈ 1,645 pour R = 1. Secundo, la montée de la courbe se fait plus abrupte, plus discriminante : cette montée serait tout à fait verticale pour une taille n → ∞ et séparerait exactement les candidats qualifiés et non qualifiés. Enfin, tertio, une quasi-certitude de sélection est atteinte plus rapidement pour une fidélité élevée. L’utilisation d’autres valeurs paramétriques de taille (n), de taux de sélection (1–P), voire de mode de détermination de la norme (linéaire, ordinale) donne lieu à des comparaisons et à des conclusions semblables.
Figure 3
Probabilité de sélection pour un candidat qualifié (V ≥ VP) pour P = 0,95, n = 200 et R variant de 0,8 à 1 (norme linéaire)
Il apparaît donc clairement qu’à la fois l’erreur de mesure et l’incertitude échantillonnale du seuil normatif apportent leur quote-part à la qualité de la sélection et au degré de légitimité de la décision qui s’ensuit. Le traitement conjoint de ces deux sources s’impose donc dans le dessein de garder sous contrôle le risque des erreurs de sélection.
Mieux contrôler, certes, mais comment le faire, alors que l’argument du contrôle et les calculs donnés en appui sont ancrés sur la valeur vraie V et sur sa connaissance, une valeur qui en pratique est inconnaissable, la seule valeur disponible étant le score X qu’obtient le candidat, un score contaminé par l’erreur de mesure ? La solution – ou, du moins, une solution – consiste à procéder à rebours et à mettre en place une « norme sûre », telle que celle que nous avons déjà proposée pour un contexte de mesure sans erreur de mesure (Laurencelle 2002, 2008a, 2008b).
Le contrôle de l’erreur de sélection maximale et la norme sûre
Le taux de sélection K, auquel correspond le seuil centile P = 1 – K marquant la zone de la sous-population à retenir[5], concerne les personnes dont le score X déborde le Pe centile, XP, de la distribution si la mesure X est dépourvue d’erreur, c.-à-d. si R = 1. En fait, ce sont ceux faisant partie de la portion des 100 × K % meilleurs candidats qui intéressent l’agence de sélection. Or, dans le cas habituel où R < 1 et les scores X sont entachés d’une erreur de mesure, les « meilleurs » à retenir ne sont plus strictement les individus qui obtiennent les meilleurs scores X ; ils correspondent plutôt à ceux qui posséderaient les meilleures valeurs vraies V, donc ceux relevant de la sous-population délimitée par l’inégalité V ≥ VP.
La population envisagée se partage donc en deux sous-populations, regroupant d’une part les individus non qualifiés pour qui V < VP et d’autre part ceux qui sont qualifiés selon V ≥ VP. Une mauvaise sélection consisterait à retenir un individu non qualifié, de valeur vraie VNQ < VP, la probabilité d’une telle occurrence pouvant s’écrire :
Contrôler l’erreur de sélection équivaut ici à réduire la probabilité d’une mauvaise sélection. Or, cette probabilité dépend primordialement de la valeur vraie du candidat examiné. Ladite probabilité sera petite si VNQ s’éloigne de la zone de qualification bornée par VP, la valeur seuil, tandis qu’elle croîtra à mesure que VNQ monte vers VP. Ainsi, le candidat non qualifié pour qui Vnq ≈ VP et Vnq ≈ VP aura la probabilité la plus grande d’être incorrectement sélectionné, autrement dit :
En plafonnant cette probabilité maximale de sélection à une valeur prédéterminée, disons α, nous pouvons enfin fixer la norme satisfaisant à cette équation, selon :
norme que nous appelons norme sûre[6] : la personne sélectionnée d’après cette norme a une probabilité d’au plus α d’être non qualifiée. Ce sont l’incorporation du terme d’erreur e dans l’équation-modèle (13) et sa solution par le calcul d’aire illustré à la figure 2 qui constituent la contribution nouvelle de cet essai.
Ainsi, plutôt que de définir la norme en nous référant à la mesure X et à son centile XP, nous la basons plutôt sur la valeur liminale VP, telle qu’à l’équation (15). Aussi, nous définissons la norme sûre C*P ou, plus précisément, sa cheville λ(P, R, n, α) par :
laquelle garantit la sélection d’un candidat qualifié selon un niveau de confiance de 1 – α. On aura compris que, dès que R < 1 ou n < ∞, nous obtiendrons C*P > XP.
La norme sûre, présentée ci-dessus dans son modèle linéaire et concrétisée par l’écart linéaire λ, peut aussi être définie plus prudemment par une statistique d’ordre X(r) tirée des n statistiques de la série normative, en en exploitant les propriétés locales à référence normale[7]. Ainsi, pour le candidat non qualifié dont la valeur V jouxte le seuil VP, l’utilisation de la statistique de rang r = P × (n + 1), correspondant à peu près au centile XP, encourrait une probabilité p donnée d’être retenu, probabilité qu’il sera possible de ramener sous α (c.-à-d. p ≤ α) en élevant le rang r vers r*(P, R, n, α), de sorte que, en posant C*P = X(r*) :
Le rang décalé r* dont est tirée la norme CP = X(r*) constitue l’équivalent ordinal de la norme linéaire λ et dépend comme elle des paramètres P, R, n et α. La théorie de distribution de la norme ordinale a été brossée dans la section précédente.
Normes sûres exigeantes ou permissives
La norme sûre exigeante, considérée ci-dessus CPexig(α), assure que l’individu non qualifié, pour qui V ≤ VP, ait une probabilité d’au plus α d’être retenu, c.-à-d., succinctement, max Pr {V + e ≥ CPexig(α) | V ≤ VP} = α. De manière complémentaire, l’application d’une norme permissive, CPperm(α), fait que les personnes qualifiées selon V ≥ VP ont une probabilité maximale α d’être rejetées, soit max Pr {V + e < CPperm(α) | V ≥ VP} = α. L’analyse montre que, en général, la norme permissive est le complément probabiliste de l’autre, soit :
Cette correspondance fait en sorte que, dans ce cas, les calculs et solutions informatiques de l’une peuvent, mutatis mutandis, servir également pour l’autre.
Sensibilité et spécificité des normes
La norme exigeante, qui assure la qualification des candidats à retenir, favorise la spécificité, que nous définissons comme le concept épidémiologique de prédictivité positive, soit :
En revanche, la norme permissive favorise plutôt la sensibilité, définie à l’ordinaire comme :
Soit QR, la probabilité qu’une personne Qualifiée soit Retenue par la norme, QR étant aussi l’espérance mathématique de la proportion de personnes qualifiées retenues dans une application. Pour une norme CP donnée, QR est évaluée par :
En posant CP = λ (norme linéaire) ou CP = Φ–1(r* / (n + 1)) (norme ordinale) dans l’intégrale (20), nous obtenons une estimation ponctuelle de QR, généralement proche de son espérance, cette dernière devant être évaluée à travers tout le domaine de CP. Finalement, l’évaluation complète de la spécificité et de la sensibilité passe par l’évaluation des espérances :
et
Notons que, dans l’évaluation en espérance de l’indice SP, le numérateur et le dénominateur sont tous deux variables, au contraire de l’indice SENS, dans lequel seul le numérateur varie. Cela a pour effet de flouter le calcul de répartition de la population et des candidats selon qu’ils sont qualifiés ou non et sélectionnés ou non : les correspondances des indices sont alors approximatives. Quant aux estimations ponctuelles, c.-à-d. celles basées sur λ ou sur r* / (n + 1) plutôt que CP, lesdites correspondances y sont exactes. Le choix de la norme, exigeante ou permissive, dépendra du contexte de la sélection.
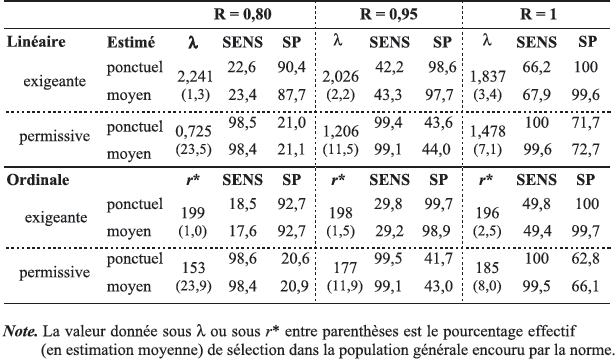
Le tableau 1 fait voir un ensemble de valeurs illustrant une situation où la base normative aurait été construite en mesurant n = 200 éléments représentatifs d’une population normale standard. Trois niveaux de fidélité, ou d’erreur de mesure, y sont illustrés.
Tableau 1
Normes sûres exigeantes et permissives au seuil α = 0,05 basées sur un groupe normatif de n = 200 éléments à distribution normale standard selon trois niveaux de fidélité de mesure (R), leur sensibilité (SENS) et leur spécificité (SP), en mode linéaire (λ) ou ordinal (r*), la sélection visant les 5 % supérieurs de la population
Effets de la taille n et de la fidélité R
Telles qu’elles sont établies par calcul, les normes linéaire et ordinale garantissent en espérance la protection déclarée, à savoir, par exemple, qu’une personne non qualifiée n’est retenue qu’avec probabilité α par la norme exigeante, ou qu’une personne qualifiée n’est incorrectement rejetée qu’avec le même risque ; la taille n et la fidélité R ne compromettent pas vraiment cette garantie. D’un autre côté, l’accroissement de n (qui réduit la fluctuation échantillonnale de la norme empirique) et l’amélioration de R (qui rapproche le score du candidat testé de sa valeur vraie) influent sur les propriétés adventices de la procédure de sélection, en augmentant à la fois leur sensibilité et leur spécificité. Les données du tableau 1 illustrent parfaitement cet effet du paramètre R. Pour ces raisons évidentes et par honnêteté envers les candidats jugés, les décisions devraient donc se baser sur une taille normative suffisamment élevée (p. ex., de 100 à 500 personnes) et sur une mesure suffisamment fiable (p. ex., R ≥ 0,70).
Effets de la forme de distribution réelle des données
Dans un article antécédent (Laurencelle, 2015), nous avons sommairement exploré une famille de distributions asymétriques (de loi Khi-deux) pour en étudier l’impact sur la validité des normes proposées. Alors que la norme linéaire, basée sur la moyenne et l’écart-type de l’échantillon normatif asymétrique, affiche un biais qui ne se résorbe pas vraiment, la norme ordinale, quant à elle, reste sans biais, et son erreur-type, comme celle de la norme linéaire, décroît comme il se doit au fur et à mesure que la taille n augmente. L’ajout d’une erreur de mesure de forme normale à une distribution de valeurs vraies de forme asymétrique et son effet sur la fiabilité des normes présentes restent à étudier.
Exemples et discussion
Prenons l’exemple d’un test, ou système de mesure, ayant une fidélité estimée à R = 0,80, valeur plutôt typique d’une certaine catégorie de tests d’habileté. Ce test[8], étalonné sur un groupe normatif comportant n = 200 participants, serait doté d’une moyenne X̅ = 50 et d’un écart-type sX = 10. Ainsi, l’erreur-type de mesure sur X serait ![]() . Pour sélectionner dans la sous-population comprenant les 5 % × 1000 ≈ 50 de personnes plus qualifiées, la norme λ applicable, en mode exigeant, est 2,241 (cf. éq. (16) ou tableau 1), et nous calculons :
. Pour sélectionner dans la sous-population comprenant les 5 % × 1000 ≈ 50 de personnes plus qualifiées, la norme λ applicable, en mode exigeant, est 2,241 (cf. éq. (16) ou tableau 1), et nous calculons :
un nombre[9] qu’il est loisible d’arrondir à 72 ou de compléter à 73. Ainsi, ce seuil, avec la règle décisionnelle qui le complète (« Obtenir un score X ≥ 72 »), garantit qu’un candidat non qualifié ait au plus (approximativement) une probabilité de 0,05 d’être retenu. Ce seuil exigeant, et sévère, qui sous-tend un taux de sélection global de 1,3 %, possède une spécificité de 87,7 % pour une sensibilité de 23,4 %.
Supposons maintenant un bassin de 1000 candidats tirés de la population générale[10]. Sur les 1000 candidats incluant hypothétiquement 50 personnes qualifiées, il y aura (en moyenne) 1,3 % × 1000 ≈ 13 personnes retenues par le test (pour lesquelles X ≥ 72). De ces 13 personnes, l’indice de spécificité (87,7 %) propose que 11,4 ≈ 11 seraient qualifiées, contre 2 qui ne le seraient pas. Par contre, l’échantillon contenant 5 % × 1000 » 50 personnes qualifiées, les ~11 retenues dénotent une sensibilité de 11 / 50 ≈ 22 % (par rapport à l’indice plus complet de 23,4 %), notre filet plutôt serré (au seuil de 0,05) ayant laissé échapper 50 – 11 = 39 personnes qualifiées. Si le test utilisé avait été parfaitement fidèle (R = 1), c.-à-d. sans erreur de mesure, la règle applicable aurait été « Obtenir X ≥ 68 » en utilisant λ = 1,837. Sur les 3,4 % ou 34 candidats sélectionnés, pratiquement tous seraient qualifiés, selon la spécificité de 99,6 %, et le filet serait allé chercher 34 des 50 personnes qualifiées dans la cohorte, selon une sensibilité de 67,9 %.
Notre second exemple reprend le même contexte, cette fois en appliquant un seuil permissif de mode ordinal. Une raison importante qui ferait préférer la norme ordinale, rappelons-le, est que, même s’il y avait doute sur la pertinence du modèle normal global pour représenter toutes les données d’une population, il est vraisemblable que celles occupant les ailes de la distribution imitent approximativement celles de la loi normale, de sorte que les statistiques d’ordre situées aux extrémités puissent servir à imiter celles qui nous intéressent. Aussi, ces normes sont non biaisées en espérance. Ici, pour une fidélité de R ≈ 0,80, nous obtenons[11]r* = 153, soit CP = X(153:200). Supposons maintenant que, pour notre test de moyenne 50 et d’écart-type 10, l’examen des n = 200 statistiques d’ordre montre X(153) = 57, une valeur possible et que nous a proposée une simulation informatique. La règle de sélection permissive est ici « Obtenir un score X ≥ 57 ». La fraction de sélection effective dans la population, 23,9 %, est calculable ici simplement par 1 – r* / (n+1) = 1 – 153 / 201 ≈ 0,239. Pour les 1000 candidats au poste, il y aura donc environ 239 personnes retenues. La spécificité de 20,9 % nous permet d’espérer que 50 d’entre elles seront qualifiées (contre 189 qui ne le seront pas !), alors que notre collecte aura permis de recruter pratiquement toutes les personnes qualifiées, grâce à la sensibilité de 98,4 %.
Épilogue et conclusion
Les ouvrages de référence sur la mesure en sciences humaines et la psychométrie, qu’ils soient anciens (Gulliksen, 1950 ; Guilford, 1954) ou plus récents (Traub, 1994 ; Nunnally & Bernstein, 1994 ; Bertrand & Blais, 2004 ; Brennan, 2006), traitent tous de l’erreur de mesure, un ingrédient essentiel à la base de la doctrine algébrique désignée théorie des tests classique. L’erreur de mesure est liée au concept de fidélité psychométrique ; c’est une composante à variation aléatoire qui reflète un certain flou dans la mesure répétée chez la même personne, évaluée dans des conditions semblables. Parfois, l’erreur de mesure, ou plutôt, « l’erreur-type de mesure », servira à déterminer l’intervalle de confiance ceignant un score obtenu et bornant la « valeur vraie » sous-jacente avec une probabilité définie. L’erreur de mesure, rapportée au concept psychométrique de fidélité (notre coefficient R), servira à expliquer la variance des mesures en dégageant la part des différences réelles entre les personnes de celle due aux fluctuations aléatoires. La fidélité servira aussi à « désatténuer » le coefficient de validité prédictive ou concomitante d’un test selon la portion d’erreur contenue dans chaque ingrédient, etc. (voir aussi Ree & Carretta, 2006). Ces développements et applications restent pratiquement tous d’ordre algébrique : nulle part, nous n’avons trouvé de traitement probabiliste de l’erreur de mesure en psychométrie ni de la théorie distributionnelle des ingrédients et indices formant la théorie des tests. Pour le cas de la décision psychométrique, celle consistant à catégoriser une personne après avoir obtenu son score à un test (acceptée/refusée ; diagnostiquée positive/non diagnostiquée ; classée dans la catégorie j, 1 ≤ j ≤ k ; etc.), certains auteurs recommandent la prudence et de « tenir compte de l’erreur », sans plus.
Or, tout algébrique que soit sa base, la théorie des tests est aussi une application statistique, par le fait même de la présence essentielle de l’erreur de mesure, à laquelle est associé généralement le modèle de la loi normale, et aussi par son recours à des échantillons probabilistes de personnes évaluées. Cette dimension statistique à double volet a une incidence assez large, notamment dans la modélisation factorielle classique (Girshick, 1936) ou dans la validation de modèles en équations structurelles (voir p. ex. Lomax, 1986), pour ne citer que ces exemples. Cette dimension se concrétise aussi, et de façon aiguë, dans l’utilisation des tests à des fins de sélection, de qualification et de catégorisation. Dans ces cas, l’erreur a des conséquences pour les personnes, leur carrière et leur vie, et le psychométricien a l’obligation professionnelle d’en assumer la responsabilité.
Dans le présent développement, qui continue celui commencé plus tôt (Laurencelle, 1998, 2008b, 2015), nous avons voulu défricher un secteur de cette psychométrie statistique, celui concernant la décision normative, et nous l’avons illustré en élaborant une théorie basée sur les modèles simples que sont la loi normale de l’erreur de mesure et la distribution normale des scores d’un test. Nous avons aussi proposé une règle de contrôle pouvant servir à justifier la décision normative et à la défendre en justice, en cas de litige. Cependant, il est facile d’imaginer des situations pour lesquelles les modèles présentés ici seraient inadéquats ou d’une utilité douteuse, par exemple un modèle de distribution de scores de type lognormal ou Gamma (Laurencelle, 2015), binomial ou autre. De tels exemples sont non seulement possibles, mais ils sont couramment rencontrés, et seul un traitement adapté et rigoureux peut leur rendre justice. C’est dire que, même dans ce petit secteur de la psychométrie statistique, il reste beaucoup à faire.
Pour illustrer davantage les applications de ce qui précède, nous présenterons, dans un prochain article en Partie III, des exemples détaillés de développement de normes et de protocole d’évaluation normative, et ce, dans des contextes variés. Des tables indicatives de normes sûres (avec les indices correspondants de sensibilité et de spécificité) seront aussi fournies. Une section de l’article examinera la robustesse des normes et du contrôle de l’erreur pour des contextes où le postulat de normalité du score X n’est pas retenu. Enfin, la seconde édition de notre Étalonnage et la décision psychométrique (Laurencelle, 2016) propose, en section F, des tables extensives des normes linéaire et ordinale, tout en récapitulant la théorie et en articulant les applications esquissées dans les parties I et II de cet essai.
Appendices
Notes
-
[1]
Nous traitons ici de sélection critériée, exigeant que le candidat retenu présente un score qui déborde une valeur de référence (XP), et non de sélection relative dans laquelle les n candidats présentant les meilleurs scores sont retenus, à quelque niveau que se situent ces scores. Ainsi, le taux de sélection (ou capture) K désigne-t-il la fraction de population visée par l’organisme intéressé, et non la fraction ou le nombre de personnes effectivement retenues.
-
[2]
Prenons l’exemple de P = 0,90 et R = 0,75. Au lieu des 10 % attendus de valeurs vraies captées, l’utilisation de V* = R × E(XP) en retiendrait 13,4 %, soit un excédent de 3,4%, ou 34% de plus qu’attendus.
-
[3]
Soit Pr {V + e > XP} = Pr {e > XP – V} = Pr {e /
 > (XP – V) /
> (XP – V) /  } = 1 – Φ{ (XP – V) /
} = 1 – Φ{ (XP – V) /  } = 0,160, où Φ est la fonction de répartition de la loi normale standard.
} = 0,160, où Φ est la fonction de répartition de la loi normale standard. -
[4]
La fonction de répartition correspondant à la densité (10) n’a pas d’expression simple : voir Johnson, Kotz et Balakrishnan (1995).
-
[5]
Nous considérons ici la sélection d’individus situés dans la zone supérieure de la population, l’argument et les calculs pouvant aussi bien être calqués après inversion pour ceux de la zone inférieure, pour laquelle P = K.
-
[6]
La solution de cette équation [ou inéquation, dans le cas de l’équation (17)], consiste à repérer λ pour l’équation (16) ou X(r*) pour l’équation (17) en égalisant l’intégrale
 à α, expression dans laquelle FCp(x) est la fonction intégrale de (10) et
à α, expression dans laquelle FCp(x) est la fonction intégrale de (10) et  .
. -
[7]
Une norme dite non paramétrique est aussi possible, laquelle n’invoque aucun modèle de distribution incluant le modèle normal. Il s’agit de la norme ordinale non paramétrique, laquelle assure le contrôle d’erreur pour l’incertitude échantillonnale, mais non pour l’erreur de mesure (voir Laurencelle, 2016).
-
[8]
Ce sont la moyenne et l’écart-type bruts du test que nous avons ici en tête. Toutefois, l’argument et les calculs valent également pour des données transformées (par une conversion linéaire), comme on le pratique pour les échelles standardisées (score T, QI, etc.).
-
[9]
L’impact de ces simplifications de la norme calculée peut être supposé minime relativement à toutes les autres incertitudes présentes dans l’environnement de ce calcul, incluant celles liées à la pertinence ou à l’adéquation du modèle normal.
-
[10]
10. Dans des circonstances plus réalistes de sélection, le bassin de candidats se présentant pour un emploi et pour un test comportera fréquemment des candidats disposés à l’emploi convoité, de sorte que la sélection porterait plutôt sur une sous-population ayant un niveau d’aptitude (ou d’adéquation) plus élevé que celui caractérisant la « population générale ».
-
[11]
11. Le seuil ordinal garantit le niveau de probabilité a sous forme d’une inégalité, p. ex. Pr {VP + e ≥ CP) ≤ α plutôt qu’une égalité, l’intervalle de probabilité couvert entre une valeur de seuil (p. ex., r = 153) et les valeurs voisines (r = 152 et 154) pouvant être assez grand (et ce, de façon inversement proportionnelle à la taille normative n).
Bibliographie
- Bertrand, R. & Blais, J.-G. (2004). Modèles de mesure : l’apport de la théorie des réponses aux items. Québec : Presses de l’Université du Québec.
- Brennan, R. L. (2006). Educational measurement (4th ed.). Westport, CT: American Council on Education.
- David, H. A. (1981). Order statistics (2nd ed.). New York: Wiley.
- Girshick, M. A. (1936). Principal components. Journal of the American Statistical Association, 31, 519-528. doi: 10.1080/01621459.1936.10503354
- Guilford, J. P. (1954). Psychometric methods (2nd ed.). New York: McGraw-Hill.
- Gulliksen, H. (1950). Theory of mental tests. New York: Wiley.
- Johnson, N. L., Kotz, S., & Balakrishnan, N. (1995). Continuous univariate distributions, Vol. 2 (2nd ed.). New York: Wiley.
- Laurencelle, L. (1998). Théorie et techniques de la mesure instrumentale. Québec : Presses de l’Université du Québec.
- Laurencelle, L. (2002). L’incertitude des seuils statistiques et l’établissement d’une norme de qualification sûre. Mesure et évaluation en éducation, 25(2-3), 19-33.
- Laurencelle, L. (2008a). L’établissement d’une norme de qualification sûre dans un contexte non paramétrique. Tutorials in Quantitative Methods for Psychology, 4, 1-12. Repéré à http://www.tqmp.org/RegularArticles/vol04-1/p001/p001.pdf
- Laurencelle, L. (2008b). L’étalonnage et la décision psychométrique. Québec : Presses de l’Université du Québec.
- Laurencelle, L. (2015). Une théorie des seuils psychométriques à double contrôle d’erreur – Partie I : l’imprécision échantillonnale des centiles. Mesure et évaluation en éducation, 38(2), 87-109.
- Laurencelle, L. (2016). L’étalonnage et la décision psychométrique (2e éd.). Québec : Presses de l’Université du Québec.
- Lomax, R. G. (1986). The effect of measurement error in structural equation modeling. Journal of Experimental Education, 54, 157-162. doi: 10.1080/00220973.1986.10806415
- Lord, F. M., & Novick, M. R. (1968). Statistical theories of mental test scores. Reading, MA: Addison-Wesley.
- Nunnally, J. C., & Bersntein, I. (1994). Psychometric theory (3rd ed.). New York: McGraw-Hill.
- Pettersen, N. (2000). Évaluation du potentiel humain dans les organisations : élaboration et validation d’instruments de mesure. Québec : Presses de l’Université du Québec.
- Ree, M. J., & Carretta, T. R. (2006). The role of measurement error in familiar statistics. Organizational Research Methods, 9, 99-112. doi: 10.1177/1094428105283192
- Traub, R. E. (1994). Reliability for the social sciences: Theory and applications (vol. 3). Thousand Oaks, CA: SAGE.
List of figures
Figure 1
Illustration de l’impact de l’erreur de mesure e sur la sélection selon le critère X = V + e ≥ XP (norme XP selon n → ∞). Le candidat considéré aurait la valeur V = 1,20. La ligne pointillée marquée 𝑓(X) représente la répartition de la population
Figure 2
Illustration de l’impact de l’erreur de mesure e sur la sélection selon le critère X = V + e ≥ CP (norme CP selon n = 200)
Figure 3
Probabilité de sélection pour un candidat qualifié (V ≥ VP) pour P = 0,95, n = 200 et R variant de 0,8 à 1 (norme linéaire)
List of tables
Tableau 1
Normes sûres exigeantes et permissives au seuil α = 0,05 basées sur un groupe normatif de n = 200 éléments à distribution normale standard selon trois niveaux de fidélité de mesure (R), leur sensibilité (SENS) et leur spécificité (SP), en mode linéaire (λ) ou ordinal (r*), la sélection visant les 5 % supérieurs de la population