Abstracts
Résumé
L’étude empirique présentée dans cet article examine le jugement évaluatif d’enseignants de l’école primaire genevoise lorsqu’ils attribuent des notes certificatives, plus particulièrement dans des contrôles écrits proposant des exercices de résolution de problèmes additifs. Les questions de recherche portent, d’une part, sur les caractéristiques des contrôles écrits élaborés par les enseignants. Elles portent, d’autre part, sur le jugement des enseignants quand ils verbalisent leur pensée en cours d’évaluation. À partir de l’analyse d’incidents critiques observés pendant la correction des travaux des élèves, les résultats de recherche donnent à voir la préoccupation des enseignants à comprendre le raisonnement mathématique des élèves, les amenant à devoir faire face à des réponses imprévues et singulières qui nécessitent une spécification de leurs référents. Les analyses entreprises débouchent sur la conceptualisation de différents cas de figure entre des jugements analytiques et holistiques, dont la mise en tension constructive peut être vue comme un enjeu majeur de développement pour l’évaluation d’apprentissages complexes, dont la résolution de problèmes de mathématiques.
Mots-clés :
- évaluation certificative,
- incident critique,
- jugement,
- problèmes additifs,
- référentialisation
Abstract
This empirical study examines the assessment judgment of Geneva primary school teachers when they are required to grade students’ tests, specially for additive problem-solving exercises. The research questions relate, on the one hand, to the characteristics of the written tests drawn up by the teachers. On the other hand, they refer to the teachers’ judgment as they verbalize their thoughts during assessment. Through the analysis of critical incidents observed during the grading of students’ tests, research findings reveal a concern for teachers to understand students’ mathematical reasoning, specially to handle unexpected and singular responses leading to a specification of the assessment criteria. The analyzes undertaken lead to the conceptualization of different cases between analytical and holistic judgments whose constructive tension can be seen as a major development challenge for the assessment of complex learning activities, such as solving mathematical problems.
Keywords:
- certificative assessment,
- critical incident,
- judgement,
- additive problems,
- referentialization
Resumo
O estudo empírico apresentado neste artigo examina o juízo avaliativo dos professores da escola primária genebrina quando atribuem as notas certificativas, mais particularmente nos testes escritos que propõem exercícios de resolução de problemas aditivos. As questões de investigação dizem respeito, por um lado, às características dos testes escritos elaborados pelos professores e, por outro lado, ao juízo dos professores quando verbalizam o seu pensamento durante a avaliação. A partir da análise de incidentes críticos observados durante a correção dos trabalhos dos alunos, os resultados da investigação revelam a preocupação dos professores em compreender o raciocínio matemático dos alunos, levando-os a enfrentar respostas imprevistas e singulares que exigem uma especificação dos seus referentes. As análises realizadas levam à conceptualização de diferentes casos entre juízos analíticos e holísticos, cuja tensão construtiva pode ser vista como um grande desafio para o desenvolvimento da avaliação das aprendizagens complexas, incluindo a resolução de problemas matemáticos.
Palavras chaves:
- avaliação certificativa,
- incidente crítico,
- juízo,
- problemas aditivos,
- referencialização
Article body
Introduction
L’évaluation sommative pratiquée par les enseignants a fait l’objet de nombreuses recherches qui ont mis en évidence un ensemble de « défaillances » (Crahay, 2009). Sans viser une quelconque exhaustivité, citons les études docimologiques bien connues pour avoir dégagé des biais systématiques qui affectent le jugement de l’enseignant, dont la conséquence est de sous-évaluer ou de surévaluer les performances des élèves (p. ex., Noizet et Caverni, 1972). D’autres recherches en psychologie sociale ont montré à quel point le « jugement professoral » est sous influence de stéréotypes, liés entre autres à l’origine sociale et ethnique des élèves, à leur sexe, au fait qu’ils aient redoublé, etc. Les enseignants tendent aussi, par exemple, à privilégier les élèves qui donnent des explications causales internes à leurs comportements et apprentissages (Bressoux et Pansu, 2003). Ces recherches établissent que le jugement de l’enseignant a une fonction sociale, au-delà de la stricte appréciation des performances des élèves. Visant à comprendre pourquoi les enfants réussissent inégalement selon leur milieu social, des travaux sociologiques ont mis en évidence les normes d’excellence qui régissent les évaluations sommatives des enseignants, aboutissant à une discrimination sélective des élèves (p. ex., Duru-Bellat, 2003 ; Perrenoud, 1984). Dans une approche microsociologique, les travaux de Merle (2007) ont, quant à eux, tout particulièrement porté sur les « arrangements évaluatifs » qui se passent autour de la négociation implicite et explicite de la note scolaire. Nombre d’auteurs en sciences de l’éducation se sont aussi employés à théoriser les « affres » de l’évaluation sommative, par exemple en termes de « constante macabre » (Antibi, 2003), plaidant sans relâche pour une évaluation sans note (p. ex., Neumayer et Vellas, 2015). Il s’agirait de se « désintoxiquer » des pratiques de notation qui envahissent aujourd’hui l’ensemble des activités humaines (Meirieu, 2009).
Malgré ces nombreuses recherches dont nous n’avons donné qu’un aperçu, la plupart des systèmes éducatifs continuent à exiger des enseignants qu’ils pratiquent des évaluations chiffrées quand il s’agit de certifier les acquis des élèves. À l’exception des premiers degrés de la scolarité, la note chiffrée reste « le support roi de l’évaluation » (De Vecchi, 2014, p. 65), véhiculant le mythe d’une plus grande objectivité et équité associées à l’usage de chiffres (plutôt que de mots). Notre propos ne sera pas de poursuivre le débat sur les notes scolaires[1], mais d’étudier, avec la connaissance de ces travaux en arrière-fond, les pratiques des enseignants qui n’ont pas le choix : ils doivent attribuer des notes chiffrées. Quelles difficultés éprouvent-ils et quels obstacles rencontrent-ils ? Ne pensent-ils vraiment qu’en termes de « sanction » (de ce qui est juste/faux) ou intègrent-ils aussi des raisonnements formatifs quand ils attribuent des notes ? Si tel est le cas, de quel ordre ?
Les curricula actuels insistent sur l’enseignement et l’apprentissage de compétences dont l’évaluation ne peut pas se réduire à une évaluation « de réussite » (De Ketele et Gerard, 2005), comme en témoignent les nombreux ouvrages et articles disponibles sur la question (p. ex., Dierendonck, Loarer et Rey, 2013 ; Rey, Carette, Defrance et Kahn, 2003 ; Tardif, 2006). Dans le contexte de notre recherche, qui est la Suisse romande, les moyens d’enseignement[2] des mathématiques proposent depuis 20 ans des activités dites de « résolution de problèmes » :
L’option choisie est de confier un plus grand rôle à l’élève dans la construction de ses connaissances, de le faire agir pour abstraire, de lui demander de créer un langage pour rendre compte et communiquer, de lui faire adopter une démarche scientifique, d’élaborer ses instruments. […] L’enseignant fait comprendre à l’élève qu’il doit prendre des initiatives personnelles, choisir sa méthode, faire des essais, recommencer, car la recherche d’une solution n’est pas toujours facile et peut prendre du temps.
Gagnebin, Guignard et Jaquet, 1997, p. 9
Ce choix est en phase avec un mouvement observé dans les différents curricula nationaux et dans les évaluations internationales (PISA, TIMSS), comme l’a documenté le numéro du Dossier de veille de l’IFÉ rédigé par Feyfant (2015) sur la résolution de problèmes de mathématiques au primaire. Ce dossier met en avant la pauvreté des résultats de recherche sur l’évaluation des compétences à résoudre des problèmes de mathématiques. Il plaide pour plus d’évaluations formatives, intégrées à l’enseignement, en tant « qu’alternatives à une évaluation sommative, de contrôle de résultat » (Feyfant, 2015, p. 15). Un hiatus existe toutefois à penser que l’évaluation qui sert à certifier[3] peut être remplacée par des évaluations formatives, alors que leurs fonctions sont différentes[4]. Comme nous l’avons développé dans Mottier Lopez et Laveault (2008), l’évaluation certificative souffre de sa « mauvaise réputation ». Il est essentiel pourtant de poursuivre les études sur une pratique qui est pleinement constitutive de l’activité professionnelle de l’enseignant, pour laquelle il se dit souvent démuni quand il s’agit de juger et certifier l’acquisition de compétences par les élèves (Mottier Lopez, Tessaro, Dechamboux et Morales Villabona, 2012). Le but de cet article est de s’intéresser à ce jugement, plus particulièrement quand l’enseignant est contraint à attribuer une note certificative à des résolutions de problèmes.
La partie suivante de l’article présente les catégories conceptuelles retenues pour étudier le jugement en acte de l’enseignant, puis les questions de recherche. Le contexte de notre étude et son cadre méthodologique sont ensuite exposés, suivis des résultats organisés en deux parties. La première partie décrit les traits caractéristiques des évaluations certificatives observées. La deuxième présente l’analyse des verbalisations des enseignants pendant qu’ils corrigent les résolutions de problèmes additifs de leurs élèves. Dans une discussion conclusive, nous conceptualisons les jugements analytiques et holistiques observés au regard des différents types de problèmes additifs en jeu dans l’évaluation certificative.
Cadre conceptuel de l’étude
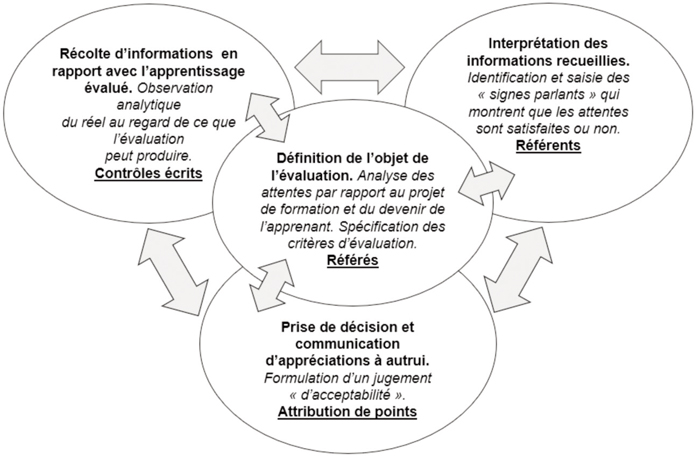
Parmi les nombreuses entrées possibles pour étudier les pratiques évaluatives des enseignants, nous retenons des catégories conceptuelles visant à dégager « la nature ontologique de l’évaluation des apprentissages des élèves, autrement dit les traits invariants qui caractérisent et organisent l’activité évaluative par rapport à d’autres activités » (Mottier Lopez, 2017, p. 173). Allal (2008) énonce les opérations propres à l’évaluation comme suit : « (1) la définition de l’objet d’évaluation, (2) la récolte d’informations concernant les conduites des apprenants en rapport avec l’objet choisi, (3) l’interprétation des informations recueillies, (4) la prise de décision et la communication d’appréciations à autrui » (p. 311). La figure 1 met en perspective ces opérations avec les implications qui en découlent pour, selon Hadji (2012), les « grandes tâches » exigées par la « dynamique de l’agir évaluatif » (en italique dans la figure 1). Nous y ajoutons les unités qui seront plus particulièrement étudiées dans notre recherche (en souligné dans la figure 1).
Figure 1
Catégories qui caractérisent l’activité évaluative et unités étudiées
Sans entrer dans de longs développements – certaines catégories seront reprises dans les résultats que nous présenterons –, précisons que ces éléments sont conçus dans une relation dynamique entre eux, comparativement aux premières conceptions, qui les pensaient plutôt en étapes successives.
Ainsi, sur le plan conceptuel, l’activité évaluative suppose une appréhension de l’objet évalué. Dans notre étude, il s’agira de résolutions de problèmes additifs au sens de Vergnaud (1981, 1982) regroupant les problèmes dont la solution demande une addition ou une soustraction. L’appréhension de l’objet évalué, au sens d’Allal (2008), s’observera par l’analyse du plan d’études concerné et par les critères d’évaluation retenus par l’enseignant en tant que « référents » (Figari et Remaud, 2014). La collecte d’informations se réalisera par le moyen de « contrôles écrits » (CE), terme qui désigne tout instrument d’évaluation composé d’items écrits (questions, consignes, problèmes, etc.) auxquels l’élève doit répondre par écrit. Ces CE sont élaborés par les enseignants en fonction des résolutions de problèmes (RP) qu’ils veulent évaluer. L’appréciation de la production de l’élève implique de leur part une identification de « référés », autrement dit de « signes parlants » (Hadji, 2012) produits par l’élève à partir desquels l’enseignant juge la production de l’élève au regard de ses attentes (référents). La prise de décision constitutive du jugement de l’enseignant consistera, dans notre recherche, à l’attribution de points donnés à chaque exercice du CE, nécessaire à la fabrication de la note.
À la suite des travaux de Vergnaud (1987), la notion d’invariant renvoie à une forme d’organisation de l’activité – ici évaluative – dont la finalité commune (ou classe de situation), dans notre étude, est de procéder à une évaluation certificative, plus particulièrement pour fabriquer une note chiffrée à partir de points attribués à des exercices mathématiques réunis dans un même CE. L’appréhension de ces invariants sera examinée à l’aune de nos catégories conceptuelles (voir Figure 1) afin d’étudier ensuite plus spécifiquement les hésitations et les difficultés que les enseignants rencontrent par rapport à « l’acceptabilité » d’une production d’élève qui ne serait pas totalement conforme à leurs référents et qui les met dans une situation de doute, voire de dilemme, quant à leur « règle » d’attribution des points. Nous conceptualiserons chaque cas en termes d’incident critique, dont l’intérêt est de « grossi(r) des phénomènes qui restent peu visibles lorsque tout fonctionne “normalement”. Il permet de saisir en condensé le fonctionnement ordinaire et extraordinaire des institutions » (Loquet, Garnier et Amade-Escot, 2002, p. 100).
Questions de recherche
Dans un premier temps, nous examinerons les caractéristiques générales des CE élaborés par les enseignants pour évaluer les RP additifs de leurs élèves : Comment les enseignants élaborent-ils leurs CE ? Quels types de problèmes retiennent-ils ? Comment le CE est-il passé en classe ? Puis, dans un second temps, nous étudierons les incidents critiques en cours d’évaluation certificative : Que nous dévoilent-ils sur le jugement évaluatif de l’enseignant quand il verbalise sa pensée en cours de correction ? Qu’est-ce qui caractérise sa posture évaluative par rapport aux enjeux de l’évaluation de RP additifs ?
Contexte de l’étude et cadre méthodologique
Années d’études concernées et enseignants-participants
En Suisse romande, la RP additifs est un des contenus d’enseignement majeurs en 5e année du primaire (5P ; élèves de 8-9 ans) et en 6e année HarmoS du primaire (6P HarmoS[5] ; élèves de 9-10 ans ; voir un extrait du Plan d’études romand en annexe 1). Pour cette étude[6], nous avons retenu 10 enseignants volontaires (voir Tableau 1 plus bas) qui enseignaient en 5PH lors de la première année de la recherche, puis en 6PH l’année suivante. Dans cet article, nous n’étudierons pas le caractère longitudinal de notre étude.
Tous les enseignants ont été observés avec la même volée d’élèves les deux années consécutives, et aucun d’eux n’avait lu ni corrigé les copies des élèves avant l’observation du chercheur. Ces 10 enseignants proviennent de cinq établissements scolaires genevois d’un niveau socio-économique contrasté.
Observation des pratiques d’évaluation certificative et collecte des données
L’observation a eu lieu de janvier à février 2012 dans les classes de 5PH, puis de février à avril 2013 en 6PH. Concrètement, et conformément au contrat de recherche préalable, chaque enseignant devait contacter un membre du groupe de recherche[7] au moment où il s’apprêtait à corriger les travaux de ses élèves. Chaque observation, d’une durée moyenne de 60 minutes, s’est déroulée en trois temps successifs :
Un entretien semi-dirigé en introduction fondé sur un canevas portant notamment sur la description des modalités de conception du CE, sur les objectifs visés, sur l’inscription de l’évaluation dans le temps d’enseignement, sur les choix évaluatifs (points, barème) ainsi que sur la description de chaque élève concerné par la correction.
Une verbalisation de l’enseignant pendant qu’il corrigeait successivement quatre épreuves écrites d’élèves, à partir de la méthode de la pensée à voix haute (think-aloud) dans une approche qualitative (Charters, 2003). Les élèves choisis par l’enseignant devaient être d’un niveau scolaire moyen à faible dans la discipline concernée. La recherche dans Lafortune et Allal (2008) a en effet montré que les enseignants tendent à verbaliser tout particulièrement avec ce profil d’élèves.
Un entretien semi-dirigé de clôture, sollicitant des remarques de l’enseignant à propos de la correction effectuée et des résultats obtenus par les élèves.
Les échanges ont été enregistrés et intégralement transcrits en verbatims. L’ensemble des traces écrites (travaux des élèves, corrigé de l’enseignant et tout autre document utilisé pendant la correction) a été photocopié. Cela représente en tout 20 observations (regroupant chacune les phases d’entretien et la séquence de verbalisation) et 80 copies d’élèves. Au total, 252 exercices de RP ont été corrigés par les enseignants.
Analyse des données
Chaque CE a fait l’objet d’une analyse de contenu : domaines et objectifs annoncés dans l’entête de l’épreuve, nombre d’exercices de RP et pondération de ceux-ci par rapport à l’ensemble du CE. Une analyse a été faite de chaque RP à partir des catégories suivantes : type de problème (selon la typologie de Vergnaud, 1981, 1982), couverture numérique, difficulté du calcul numérique et combinaison de calculs pour résoudre le problème, données à sélectionner dans l’énoncé et phrase-réponse (lacunaire ou à rédiger intégralement par l’élève). Cette analyse a été triangulée avec les verbalisations des enseignants afin, notamment, d’inférer les critères d’évaluation par rapport aux points attribués à chaque RP.
Les deux phases d’entretiens semi-structurés ont fait l’objet d’une analyse de contenu en lien avec les axes thématiques délimités par le canevas d’entretien (voir plus haut). Quant aux verbalisations pendant la correction, elles ont été analysées en plusieurs étapes. Nous avons commencé par un découpage du verbatim, exercice après exercice[8], tout en gardant la chronologie de la correction. Puis, nous avons ciblé les verbalisations qui concernent plus spécifiquement les RP et avons inséré la réponse numérisée de l’élève pour permettre une mise en perspective systématique. L’analyse du protocole a consisté à :
Inférer la logique du raisonnement évaluatif de l’enseignant au regard de la spécificité de la réponse de l’élève, à partir des catégories de l’activité évaluative définies plus haut[9] ;
Identifier les « cas » d’incidents critiques qui ont suscité des hésitations ou difficultés explicitement exprimées par l’enseignant pendant la correction. Des indicateurs précis ont été définis, montrant un changement dans la structure de verbalisation de l’enseignant (silences prolongés, reverbalisation d’éléments de la réponse de l’élève, autoquestionnement, suspension de la décision d’attribution de points, consultation d’autres copies d’élèves ou de collègues) ;
Identifier les « cas » considérés par le chercheur comme étant potentiellement significatifs d’obstacles rencontrés dans la correction, mais sans avoir été explicitement verbalisés par l’enseignant (soit celui-ci n’en a pas eu conscience, soit il les a laissés dans l’implicite).
Cette analyse a fait l’objet d’accords interjuges entre les deux auteurs de l’article au fur et à mesure des cas rencontrés et de leurs particularités. Nous avons identifié en tout 20 cas sur 128 RP corrigées en 5PH, et 26 cas sur 124 RP en 6PH.
Plus généralement, notre méthodologie s’inscrit dans une approche abductive de la recherche qualitative/interprétative. Comme l’ont définie Anadón et Guillemette (2007),
l’abduction conjugue le caractère a posteriori de la théorisation fondée sur les données empiriques avec le caractère a priori de l’utilisation inférentielle des théories (construites inductivement) pour la continuité logique de la collecte des données.
p. 35
Pour ces auteurs, la posture abductive vise à découvrir de nouvelles compréhensions des phénomènes, et non à confirmer, par l’ajout de nouvelles données, le potentiel explicatif de théories existantes.
Limites principales de l’étude
Il convient de garder à l’esprit, d’une part, que seule une minorité d’exercices corrigés comporte des incidents critiques et, d’autre part, que l’étude porte sur un profil particulier d’élèves (niveau scolaire moyen à faible) chez qui nous postulions que l’évaluation des réponses pouvait générer plus de dilemmes chez les enseignants. L’intérêt scientifique envers les incidents critiques est de dépasser l’observation de routines évaluatives en faveur de situations d’imprévus et de doutes, à partir desquelles on fait l’hypothèse qu’elles sont potentiellement révélatrices de phénomènes significatifs.
Une limite de notre étude concerne la méthode de la pensée à voix haute (think-aloud), notamment à propos de la capacité (plus ou moins avérée) des personnes à énoncer spontanément leur pensée pendant qu’elles réalisent une tâche, sachant aussi que la pensée n’est jamais totalement accessible ni totalement dicible (voir Charters, 2003, pour des développements). La triangulation méthodologique (Denzin, 1978) que nous avons effectuée entre données verbales et écrites est fondamentale pour réduire l’incertitude de l’interprétation des verbalisations. Enfin, citons la limite bien connue rattachée à la présence du chercheur, qui peut conduire à un biais de désirabilité sociale susceptible de tronquer en partie l’authenticité de la pratique professionnelle observée et verbalisée.
Description de traits caractéristiques des contrôles écrits : conception, contenu, passation
Les descriptions présentées dans cette première partie de résultats s’appuient sur l’analyse des contenus des CE et des entretiens semi-dirigés.
Conception du contrôle écrit dans des modalités collaboratives
Tous les enseignants décrivent des modalités de collaboration avec des collègues de leur établissement scolaire pour concevoir leurs contrôles écrits[10]. Soit la collaboration concerne l’ensemble des enseignants de la même année d’études de l’établissement, soit elle se fait avec un collègue en particulier. En bref, un enseignant, à tour de rôle, a la responsabilité de faire une première proposition de CE. Celle-ci est soumise aux collègues, qui la relisent et la modifient au besoin. Dans certains établissements, les modifications apportées doivent être acceptées par tous – les CE sont exactement les mêmes ; ils sont soumis aux élèves le même jour, au cours de la même demi-journée (le matin est privilégié). Dans d’autres établissements, il est admis qu’un enseignant puisse apporter une modification uniquement pour sa classe par rapport à l’enseignement effectué. Pour choisir les exercices, les enseignants disent s’inspirer des CE des années précédentes, élaborés par eux ou par des collègues. Ils disent s’inspirer aussi des exercices présentés dans les moyens d’enseignement. En 6PH, plusieurs enseignants mentionnent les « épreuves cantonales » produites par l’institution scolaire dans le but de préparer les élèves à cette épreuve externe effectuée à la fin de l’année scolaire (entre un et trois mois après notre observation en 6PH).
Contenu des contrôles écrits : domaines mathématiques et part prise par les résolutions de problèmes additifs
Au moment de notre recherche, les prescriptions institutionnelles du cycle moyen de l’école primaire genevoise indiquaient que les CE en mathématiques devaient :
comporte(r) prioritairement des situations-problèmes. L’enseignant, s’il l’estime nécessaire, peut ajouter un ou deux problèmes d’application qui lui permettent d’évaluer la maitrise technique d’outils. Dans l’appréciation, le poids des situations-problèmes est plus important.
République et Canton de Genève, 2012, p. 58
Les RP sont explicitement désignées comme des « situations-problèmes » qu’il s’agit donc de privilégier dans les évaluations certificatives. Dans ce même document institutionnel, il est exigé de la part des enseignants qu’ils formulent dans un « entête[11] » les objectifs visés par le CE donné aux élèves, le seuil de réussite général, le barème et la note. Les objectifs doivent correspondre aux contenus du Plan d’études romand (PER) organisés en cinq domaines : espace, nombres, opérations, grandeurs et mesures, modélisation. Le dernier domaine doit « s’activer dans les autres axes[12] » sans être travaillé pour lui-même.
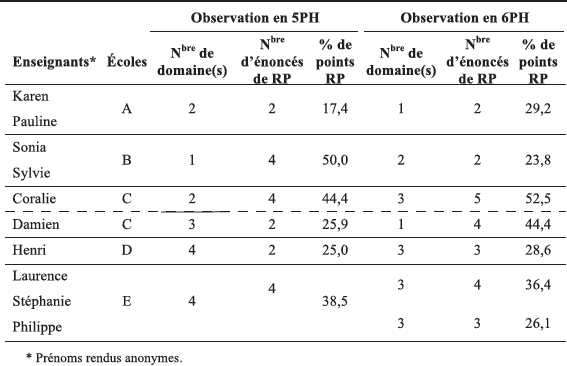
Afin d’avoir une vue d’ensemble des CE et des choix effectués par les enseignants, le tableau 1 indique le nombre de domaines ainsi que la part prise par les exercices de RP additifs.
Tableau 1
Composition des contrôles écrits et part prise par les exercices de résolution de problèmes
Les choix sont contrastés. Les CE de 5PH concernent de un à quatre domaines mathématiques et ceux de 6PH, de un à trois domaines. La plupart des CE convoquant deux domaines concernent les nombres et les opérations. Pour ce qui est des RP dans le domaine « opérations » (entre deux et cinq énoncés par CE), elles représentent entre 17,4 % et 52,5 % de la valeur de l’épreuve (pourcentage de points attribués aux RP du domaine « opérations » par rapport au total de points du CE). D’une façon générale, les CE des enseignants ne sont donc pas composés majoritairement de RP, comme le demandent les prescriptions institutionnelles.
Problèmes additifs soumis aux élèves
L’annexe 1 présente les objectifs d’apprentissage et les contenus du PER portant sur la RP additifs (domaine « opérations ») pour les quatre années du cycle moyen (8-12 ans). Pour les deux premières années d’études concernées par notre recherche, le PER indique l’apprentissage de RP additifs de composition d’états (EEE : deux états se composent pour donner un nouvel état), de transformation d’un état (ETE : transformation d’un état initial en un état final), de comparaison d’états (ECE : une comparaison de deux mesures ou de deux états).
Dans les CE de 5PH
Aux dires des enseignants (excepté Henri), c’est la première fois qu’ils évaluent des RP additifs dans des épreuves certificatives, c’est-à-dire débouchant sur une note chiffrée[13] sur une échelle de 1 à 6, note qui entrera ensuite dans une moyenne de notes servant à la décision de promotion à la fin de l’année d’études. Il apparaît donc d’autant plus intéressant d’observer quels types de problèmes ils proposent aux élèves dans leurs CE, puis ceux qu’ils proposent une année plus tard.
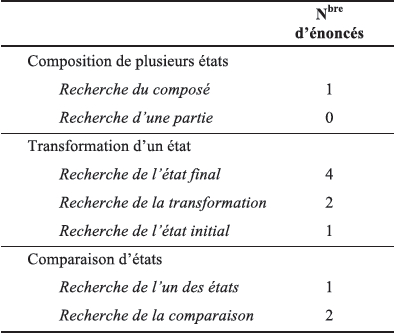
Notre corpus de 5PH comporte en tout 18 énoncés différents. (Rappelons que plusieurs CE sont identiques entre enseignants ; voir Tableau 1). À l’exception d’un énoncé impliquant un produit cartésien, tous sont des problèmes additifs. Au total, 11 énoncés engagent exclusivement une relation entre trois variables numériques. Par rapport à la catégorisation du PER, fondée sur la typologie de Vergnaud (1981, 1982 ; Vergnaud et Durand, 1976), le tableau 2 présente la catégorisation de ces 11 énoncés.
Tableau 2
Catégorisation des RP en 5PH selon la typologie de Vergnaud
Les travaux de Vergnaud et de ses successeurs (p. ex., Brun et Schubauer-Leoni, 1981 ; Conne, 1984) ont montré que les types de problèmes additifs ne sont pas du même ordre de difficulté, non seulement au regard de la structure relationnelle impliquée (p. ex., un problème de recherche de l’état final[14] est plus facile à résoudre qu’un problème de recherche de l’état initial[15]), mais également au regard de la formulation des énoncés (ordre d’introduction des données, mots choisis, place de la question), de la complexité du calcul numérique, etc. Nous renvoyons le lecteur aux auteurs cités pour plus de développements à ce propos. En bref, retenons que, dans notre corpus :
La majorité des résolutions impliquent une seule mise en relation numérique. Sept énoncés sur 18 impliquent, quant à eux, plus d’une mise en relation, avec la combinaison de plusieurs opérations ;
Les enseignants tendent à privilégier les problèmes de transformation d’un état. Tous proposent au moins un problème de recherche de l’état final, excepté Henri (qui, rappelons-le, a déjà précédemment évalué des RP) ;
C’est la transformation positive qui est majoritaire dans les 18 énoncés ;
La couverture numérique des problèmes va de la première dizaine à la première centaine, excepté Henri (au-delà de 400) ;
La question du problème est majoritairement formulée à la fin de l’énoncé ; les élèves doivent répondre par une phrase complète (excepté pour les trois enseignants de l’établissement E, qui privilégient un nombre-réponse à indiquer dans une phrase lacunaire prérédigée) ;
Ces trois enseignants sont également les seuls à proposer des énoncés (deux sur quatre) qui demandent aux élèves de sélectionner, parmi un ensemble de données numériques, les données pertinentes à utiliser pour répondre à la question du problème.
Au-delà des quelques éléments communs cités, la variation entre les problèmes est importante, y compris sur le plan de leur formulation : pour certains, avec des énoncés brefs et présentant les informations dans l’ordre logique de l’opération intellectuelle impliquée ; pour d’autres, avec des énoncés beaucoup plus complexes (y compris avec des mots pouvant être contre-intuitifs par rapport à la relation numérique en jeu).
Dans les CE de 6PH
Parmi les 23 énoncés différents qui composent le corpus de 6PH pour le domaine « opérations », 9 sont des problèmes additifs. Les autres sont des problèmes multiplicatifs. Sur ces 9 problèmes, 2 n’impliquent qu’une seule mise en relation entre trois éléments ; tous les autres nécessitent plusieurs mises en relation et une combinaison d’opérations pour répondre à la question du problème. Comparativement aux énoncés de 5PH, c’est une des grandes différences, ainsi que la couverture numérique, qui dépasse le millier pour la plupart des problèmes.
Des constats plus détaillés pourraient évidemment être posés à propos des caractéristiques des problèmes choisis par les enseignants et des conséquences sur les stratégies de résolution des élèves. Notre description à grands traits vise uniquement à faciliter la lecture de l’analyse suivante des incidents critiques.
Conditions de passation des contrôles écrits
Aux dires des enseignants, la plupart des CE sont calibrés pour être réalisés sur une durée d’une à deux périodes de 45 minutes. Aucun des enseignants ne déclare limiter le temps aux élèves. Les enseignants considèrent en effet que la différence de rythme entre les élèves ne doit pas être un facteur de réussite ou d’échec. Tous les enseignants lisent les consignes des exercices aux élèves. Une nuance s’observe : certains enseignants choisissent de ne pas lire les énoncés des RP, considérant que cette lecture fait partie de la compétence à évaluer. D’autres les lisent, mais précisent faire attention à ne pas donner des indices de résolution. Il leur paraît important de s’assurer que les élèves comprennent les mots figurant dans les énoncés. Les élèves peuvent poser des questions avant de commencer l’évaluation. Ce temps est collectif, tout comme la lecture des consignes par l’enseignant. Les enseignants disent accepter de répondre aux questions des élèves pendant la réalisation du CE, tout en les encourageant à un travail autonome. Aucune ressource autre que des feuilles de brouillon n’est mise à la disposition des élèves pendant l’évaluation. D’une façon générale, les pratiques entre les enseignants sont très proches pour ce qui concerne les conditions de passation des CE. Elles ne semblent pas être foncièrement différentes entre la 5PH et la 6PH.
Analyse des incidents critiques en cours d’évaluation
Cette deuxième partie des résultats présente notre analyse des verbalisations des enseignants, triangulée aux analyses des énoncés de RP et des traces écrites des élèves. Trois axes émergent de l’analyse : 1) la préoccupation des enseignants à comprendre le raisonnement des élèves ; 2) une posture de valorisation de ces raisonnements ; et 3) une nécessaire spécification des référents, qui ne va pas sans poser problème quand il s’agit d’attribuer des points. Ces axes s’interpénètrent et les exemples concrets exposés ci-dessous prennent également sens les uns par rapport aux autres. Les verbatims retenus sont emblématiques des axes dégagés. Nous commençons par présenter des résultats détaillés pour la 5PH, puis nous procédons par comparaison en fin de partie pour la 6PH.
Une préoccupation : comprendre les raisonnements des élèves considérant que tous les raisonnements ne se valent pas
En 5PH, les enseignants donnent à voir une réelle préoccupation à comprendre les raisonnements de leurs élèves. À cette période du cycle moyen, des démarches alternatives de résolution de la part des élèves sont envisagées par le PER. Dans la mesure où l’enseignant accepte des démarches qu’il n’aurait pas forcément anticipées et auxquelles il devra décider ou non d’attribuer des points, il est nécessaire pour lui de tenter de comprendre le raisonnement des élèves. L’exemple de Philippe ci-dessous est particulièrement significatif :
Cet exemple concerne un problème difficile, comparativement à d’autres problèmes de 5PH. Il nécessite la combinaison de deux opérations, dont la première est un produit cartésien (trois paquets de quatre bonbons, pouvant aussi se calculer par une addition itérée) pour rechercher une comparaison d’états (nombre de bonbons en plus pour Michel, comparativement au nombre de bonbons de Samantha).
Le cas critique exposé dans cet exemple donne à voir les référés (partie de réalité choisie ; Figari, 1994) pointés par l’enseignant sur la copie qui fondent l’inférence qu’il fait du raisonnement de l’élève pour l’évaluer à l’aune de ses référents (ce par rapport à quoi le jugement est porté ; Barbier, 1985). Le raisonnement lui semble pertinent, bien qu’incorrect dans sa mathématisation (autre critère-référent). Toutefois, Philippe ne parvient pas à comprendre le résultat annoncé (référé « 10 » sur la copie de l’élève). Il considère qu’il a alors besoin de plus d’informations pour décider de l’attribution des points - notre analyse nous permet de savoir que deux points sont dévolus à la démarche et un point l’est à la réponse. Philippe suspend sa décision afin de revenir vers l’élève pour que ce dernier lui explique son raisonnement.
Dans notre corpus, Philippe n’est pas le seul à suspendre l’attribution de points pendant la correction. Plusieurs enseignants le font également, notamment pour consulter le ou les collègues avec qui ils ont conçu le CE. Cependant, ce n’est pas pour autant systématique, comme l’exemple suivant le montre à propos d’un problème qui nécessitait également deux calculs numériques :
Cet exemple est intéressant, car Sylvie est une enseignante qui consulte sa collègue en cas de doutes ou d’imprévus. Or, ici, bien qu’elle préfère que l’élève écrive toutes les étapes de son raisonnement, elle se satisfait d’une réponse partiellement complète. Autrement dit, le critère-référent de complétude (ou caractère complet de la réponse ; Gerard, 2005) est ici secondaire par rapport au fait qu’elle comprend suffisamment le raisonnement (pertinent) de l’élève pour qu’elle attribue le point.
Nous terminons avec un contre-exemple qui montre que, parfois, l’enseignant peut aussi ne pas accepter un raisonnement qui, pourtant, n’est pas faux, mais qui ne répond pas au contrat didactique (Brousseau, 1986/1996).
Après consultation (dont nous avons enregistré l’échange), les deux enseignantes considèrent que l’élève « perd un point » en raison de sa phrase-réponse. La norme est de répondre par le résultat du calcul effectué, et non par une réponse de bon sens.
De ce premier axe, nous retenons que les enseignants de notre étude accordent une réelle importance à comprendre le raisonnement de leurs élèves. Une seule enseignante, Sonia, y semble moins attachée, restant très fidèle à son corrigé. Les pratiques observées sont cependant contrastées : certains enseignants vont relativement loin dans l’analyse des réponses des élèves « pour les comprendre », tandis que d’autres moins. Un premier obstacle rencontré par les enseignants est de comprendre ce raisonnement, notamment :
quand la trace écrite de l’élève est incomplète ou insuffisamment détaillée ;
quand il y a une incohérence ou erreur partielle dans cette trace sans pouvoir en comprendre l’origine ;
quand l’enseignant ne parvient pas, à partir des référés qu’il pointe sur la copie, à les interpréter pour inférer le raisonnement de l’élève. Nous y reviendrons.
Dans ces différents cas, les enseignants consultent volontiers leurs collègues, voire reviennent vers l’élève pour un échange avec lui. Nous observons qu’ils prennent des décisions différentes au regard des référents qu’ils valorisent. Afin d’approfondir ces premiers résultats, nous poursuivons ci-dessous sur la posture de l’évaluateur et sur les processus de référentialisation en jeu.
Une posture de valorisation des productions des élèves
Les pratiques évaluatives des enseignants se caractérisent par des postures qui découlent de systèmes de valeurs et d’attitudes dans une situation donnée :
Lorsque l’acteur adopte une posture, il a fait sienne une conception précise, une manière d’agir et de se positionner dans l’espace social. La posture montre un engagement de l’acteur dans l’activité effectuée.
Jorro, 2016, p. 5
Nos analyses mettent en évidence une posture partagée par la plupart des enseignants de notre étude, qui est celle de chercher à valoriser les réponses de leurs élèves plutôt que de pénaliser à tout prix leurs erreurs. Nous présentons ci-dessous deux exemples significatifs de cette posture, mais dans deux situations opposées. La première donne à voir une réponse erronée de l’élève.
Dans ce cas-ci, l’enseignant ne donne à voir qu’une analyse partielle de la réponse de l’élève. Ainsi, il ne verbalise pas, par exemple, le fait que l’élève a soustrait les unités (2 - 2) et additionné les dizaines (8 + 3), ni qu’il a placé correctement le soustracteur dans le calcul en ligne, mais pas dans l’algorithme en colonnes qui sert à calculer la réponse. Henri choisit d’attribuer un point « pour l’unité », dont nous faisons l’hypothèse qu’il s’agit de l’unité de valeur (bouteilles) indiquée dans la phrase-réponse de l’élève. Cette hypothèse s’appuie sur l’entretien de préverbalisation, dans lequel Henri explique :
J’insiste aussi beaucoup sur l’unité, c’est-à-dire qu’ils doivent chaque fois me préciser le résultat, plus de quoi on parle. […] C’est-à-dire que là on parle de bouteilles, donc je veux voir apparaître le mot bouteilles dans le résultat. […] Je le répète constamment […] pour donner un sens au problème.
Verbatim
Du point de vue de l’activité évaluative, l’attribution du point se justifie par la microculture de classe (Mottier Lopez, 2008) d’Henri, dans laquelle la norme est de devoir indiquer dans la phrase-réponse l’unité de valeur pour « donner du sens » au nombre-réponse. Malgré une résolution erronée, l’élève obtient un point pour avoir indiqué cette unité, qui fait tout particulièrement sens dans le contexte de sa classe et que l’enseignant veut valoriser, renforcer.
L’exemple suivant montre que cette posture de valorisation des réponses des élèves ne s’observe pas seulement dans des cas de raisonnements erronés.
Dans cet exemple, l’élève obtient trois points sur trois. Son erreur de signe (révélatrice de la difficulté du problème, c’est-à-dire trouver la valeur de la transformation positive en effectuant une soustraction) n’est pas pénalisée, dans la mesure où il a calculé une soustraction. L’enseignante corrige la copie et précise qu’elle l’expliquera ensuite à l’élève. L’erreur ne sera pas ignorée, mais sera traitée autrement que par la non-attribution d’un point.
Nous observons que les enseignants en 5PH sont tolérants envers des imprécisions dans l’écriture mathématique des élèves, privilégiant à cette période de l’année scolaire la pertinence des raisonnements plus que leur exactitude formelle. Au fil de leur verbalisation, ils précisent : « Je trouve que c’est un petit peu dur de pénaliser […] vu que c’est les premières évaluations avec des problèmes. […] On va être indulgent » (Sylvie) ; « Tant pis pour cette fois parce que c’est la première fois qu’on faisait ça » (Laurence) ; « Je ne vais pas pinailler pour ce genre de chose » (Coralie). Pour les enseignants, l’erreur non sanctionnée demande par contre à être signalée à l’élève, soit en la corrigeant sur sa copie, soit lors d’une correction collective, soit lors d’un échange privé avec l’élève.
Une posture qui s’associe à une spécification des référents
Toutefois, cette posture de valorisation peut aussi engendrer des difficultés dans la décision d’attribuer des points, notamment quand l’enseignant a besoin de prendre en compte les multiples dimensions intervenant dans une RP pour comprendre le raisonnement mathématique de l’élève.
Cet incident critique est révélateur des nombreuses dimensions de la résolution d’un problème qui, chacune, peuvent être mises en relation avec des référents qui se dévoilent au fil du jugement évaluatif de l’enseignant. C’est tout particulièrement le cas quand ce dernier postule que la démarche entreprise par l’élève répond à une logique qu’il cherche à « reconnaître » et valoriser. Dans le cas de Laurence, elle mentionne les référents suivants au fur et à mesure de son interprétation évaluative, dans l’ordre de la verbalisation : pertinence du traitement de l’information, pertinence de la relation mathématique choisie (plus précisément celle qui répond à la question du problème dans la recherche de comparaison), respect de la technique opératoire de la soustraction, exactitude de la représentation du problème et exactitude de la réponse par rapport à la soustraction posée. L’enseignante est encline à valoriser le fait que l’élève a identifié la relation mathématique pertinente et qu’il a effectué une soustraction, même si celle-ci n’est pas correcte sur le plan opératoire, ni pertinente au regard du deuxième état à comparer (dont il faut calculer la valeur : trois paquets de quatre bonbons). Aux yeux de l’enseignante, l’élève « n’a pas tout faux ». Bien que l’élève n’ait pas trouvé le nombre de bonbons de Samantha, Laurence hésite, mais elle ne prendra pas de décision sans consulter ses collègues. Finalement, l’élève n’obtiendra aucun point.
Nos analyses des incidents critiques pourraient laisser entendre que les enseignants ajustent constamment leurs référents en fonction de la singularité des productions des élèves et des points à attribuer à chaque problème. Ce phénomène d’ajustement est bien connu dans la littérature citée dans l’introduction de l’article, examiné dans les études docimologiques en termes « d’effets » d’influence (p. ex., l’effet d’assimilation quand l’enseignant prend en compte des informations propres à la personne de l’élève ; Noizet et Caverni, 1972) ou examiné dans une approche microsociologique en matière « d’arrangements évaluatifs » visant essentiellement à « favoriser la mobilisation scolaire » des élèves (Merle, 2012, p. 92). Pour notre part, nous appréhendons ce phénomène d’ajustement à la lumière du processus de référentialisation (Figari, 1994 ; Figari et Remaud, 2014 ; Mottier Lopez, 2017 ; Mottier Lopez et Dechamboux, 2017) propre à l’activité évaluative. Ce processus désigne une « recherche de références pertinentes (c.-à-d. à la fois universelles et particulières) » (Figari, 1994, p. 48) susceptible de remettre en question des critères préexistants, de définir de nouveaux critères et, toujours, de spécifier les attentes.
Les incidents critiques présentés plus haut donnent à voir les critères d’évaluation que les enseignants considèrent. Certains sont préexistants, expliqués pour justifier l’attribution des points dans l’entretien semi- structuré ou en cours de correction[17] :
1 point pour la pertinence de la démarche et 1 point pour l’exactitude de la phrase-réponse (lorsque la RP vaut 2 points) ;
1 point pour la pertinence du choix du calcul, 1 point pour la maîtrise opératoire et 1 point pour la phrase-réponse (lorsque la RP vaut 3 points).
Précisons que ces choix sont conformes aux consignes institutionnelles du contexte des enseignants, lesquelles recommandent l’attribution de points « en fonction d’éléments de la démarche et du résultat » (République et canton de Genève, 2012, p. 59). Dans les épreuves externes produites par l’institution scolaire, ce sont majoritairement deux points qui sont attribués aux RP.
Nos analyses montrent que ces critères préexistants sont fonctionnels quand les réponses des élèves sont conformes aux attentes de l’enseignant, qui les applique alors scrupuleusement. Les incidents critiques donnent à voir des cas pour lesquels ils ne conviennent pas bien, conduisant à une spécification des critères au cours du jugement évaluatif. Dans l’exemple de Laurence, particulièrement révélateur, l’enseignante décortique les différentes dimensions en jeu dans la RP, verbalisant alors un plus grand nombre de critères-référents que ceux préexistants. Puis, cela ne va pas sans hésitation pour Laurence au moment de « traduire » son interprétation critériée (très formative dans l’esprit) selon les trois critères sommatifs prédéfinis. Il s’agit d’une des sources d’hésitation régulièrement éprouvée par les enseignants de notre étude, avec des questionnements tels que : Le calcul n’est pas pertinent, mais il est correctement exécuté, donc dois-je attribuer un point ? Comment puis-je évaluer la maîtrise de la soustraction si l’élève a fait une addition ? La phrase-réponse ne peut pas être juste parce que le calcul choisi n’est pas pertinent, alors que faire ? Prenons l’exemple de Karen :
Le choix de Karen sera finalement de n’attribuer aucun point dans ce cas de figure, une décision partagée également par d’autres enseignants. Les critères d’évaluation sont alors interdépendants, ce que critique la littérature spécialisée sur la question (p. ex., De Ketele et Gerard, 2005), à savoir que la réussite d’un critère (exactitude de la phrase-réponse) dépend de la réussite d’un autre critère (pertinence de la démarche). Ce n’est pas le choix de tous les enseignants, dont Philippe, qui dit : « Donc, [l’élève] ne pose pas la bonne opération. Par contre, il la calcule correctement. Il a un point. » Toutefois, pour Pauline, cette solution n’est pas optimale non plus : « [Les élèves] peuvent additionner n’importe quoi et avoir un point. » Ce type de dilemme s’observe également pour l’appréciation de la phrase-réponse, dont l’enjeu peut varier en fonction du type de problème[18], par le fait de devoir ou non indiquer l’unité de valeur (voir Extrait 4, Henri) ou par le fait d’écrire seulement le nombre-réponse ou une phrase complète reprenant les termes de la question. Autrement dit, il y a ici aussi une spécification des critères-référents propres à la phrase-réponse. Les choix varient entre les enseignants, y compris parfois entre ceux d’un même établissement scolaire qui utilisent le même CE.
Comparaison avec les RP de 6PH
Après avoir effectué les mêmes analyses pour les RP de 6PH, nous décrivons brièvement dans cette section les principaux points de comparaison par rapport aux axes dégagés plus haut. Il apparaît que la préoccupation des enseignants est toujours aussi présente à comprendre les raisonnements et démarches des élèves. Les enseignants sont par contre plus exigeants pour ce qui concerne le respect des conventions mathématiques dans les problèmes additifs, mais ils donnent à voir la même tolérance envers les problèmes multiplicatifs, qui représentent de nouveaux apprentissages évalués. Les enseignants semblent rencontrer plus de difficulté à comprendre les démarches des élèves dans les problèmes multiplicatifs que dans les problèmes additifs, avec plus d’erreurs d’interprétation de leur part. Une autre étude, en cours, ciblera ces problèmes multiplicatifs, au regard également des pratiques des deux dernières années du cycle moyen (7-8 PH) faisant partie de notre recherche plus large (Mottier Lopez et al., 2012). Pour ce qui est des problèmes additifs, les enseignants les complexifient nettement dans leurs CE de 6PH, notamment avec des résolutions qui exigent une combinaison de deux calculs numériques et plus. Les enseignants font le choix de les évaluer à partir des mêmes critères d’évaluation associés à l’attribution de deux ou trois points (rarement quatre). Les incidents critiques qui les concernent portent principalement sur la difficulté à gérer ces critères/points pour appréhender des résolutions qui engagent un nombre plus important d’opérations, comparativement aux RP de 5PH.
Discussion conclusive
Nos analyses s’inscrivent pleinement dans la lignée des travaux qui, depuis les années 1970, n’ont eu de cesse de montrer que la production d’un élève – en tant que trace à partir de laquelle l’enseignant infère l’apprentissage réalisé – est un objet construit, dont les multiples dimensions sont difficiles à isoler les unes des autres (p. ex., Bonniol, 1976, 1984, cité par Amigues et Zerbato-Poudou, 1996). Cela s’observe d’autant plus quand l’évaluation ne se réduit pas à juger la seule exactitude de la réponse attendue, mais vise à prendre en compte les démarches et raisonnements alternatifs des élèves. Nous pouvons penser que cette conception fait aujourd’hui partie de la culture professionnelle des enseignants de l’école primaire genevoise quand ils évaluent des RP, et ce, de façon cohérente avec les prescriptions institutionnelles qui encadrent leurs pratiques (plan d’études, moyens d’enseignement, prescriptions cantonales en matière d’évaluation et d’enseignement des mathématiques).
Parmi les nombreux points possibles à discuter dans cette conclusion, nous choisissons de revenir plus particulièrement sur la dynamique du jugement évaluatif critérié de l’enseignant quand il doit évaluer des RP afin de poursuivre notre projet scientifique de conceptualisation des processus de référentialisation en acte (Mottier Lopez, 2017 ; Mottier Lopez et Dechamboux, 2017). Certains travaux scientifiques font « l’hypothèse que la plupart des enseignants assimilent la fonction sommative de l’évaluation à un traitement normatif des résultats de cette évaluation » (Issaieva et Crahay, 2010, p. 37). Dans les pratiques observées dans notre étude, les enseignants fondent leur jugement avant tout sur des critères d’évaluation (référence critériée). Autrement dit, ils ne construisent pas la note scolaire en comparant les résultats des élèves entre eux (référence normative), ce qui par contre ne les empêche pas de prendre pour référence un cas rencontré dans une copie et décider par comparaison pour un autre cas. Nous observons que la comparaison entre élèves n’est jamais totalement absente, y compris quand l’évaluation se fonde sur des critères. Elle fait alors aussi office de référent à des fins, notamment, de prise de décision équitable entre élèves.
Nos analyses détaillées révèlent que le jugement évaluatif de l’enseignant oscille entre deux grandes logiques : un jugement holistique, qui désigne un jugement global de la production de l’élève, et un jugement analytique, qui se fonde sur chaque critère d’évaluation séparément (p. ex., Brookhart, 2013 ; Tardif, 2006). Ces logiques sont intéressantes à examiner finement au regard de notre analyse des incidents critiques qui, à titre de rappel, sont vus comme pouvant révéler des phénomènes propres à la pratique étudiée, y compris pour mieux comprendre les cas routiniers (quand « tout va bien »). Nos résultats permettent de dégager, en matière de tendance, les cas de figure suivants :
Quand tout va bien dans des problèmes additifs simples, un jugement holistique rapide
Dans ce cas de figure, l’enseignant donne à voir une appréhension quasi immédiate de la réponse de l’élève. Le jugement est rapide, notamment quand la résolution est conforme à ses attentes dans le cadre de problèmes additifs simples (p. ex., calcul de l’état final, avec les deux seules variables numériques indiquées dans l’énoncé, phrase-réponse canonique à rédiger). C’est également le cas quand l’enseignant constate une erreur qu’il diagnostique rapidement (p. ex., une erreur opératoire). L’enseignant enlève un point à partir du total de points dévolu à l’exercice concerné. Ce type de jugement apparaît fonctionnel.
Quand tout va bien dans des problèmes plus compliqués, un jugement analytique fondé sur les critères d’évaluation prédéfinis
Dans le cas de problèmes additifs qui sont plus ouverts à des démarches et raisonnements alternatifs, ou quand ils impliquent la combinaison de plusieurs calculs numériques par exemple, le jugement holistique n’apparaît plus aussi fonctionnel. L’enseignant a en effet besoin d’identifier et d’interpréter les différents référés (signes) sur la copie de l’élève au regard de chacun des critères-référents pour lesquels il doit décider d’attribuer ou non un point (rarement plus d’un point par critère). Quand l’enseignant ne rencontre pas de difficulté particulière à interpréter la réponse de l’élève, correcte ou (partiellement) erronée, les points attribués à chaque critère sont ensuite sommés. Nous avons constaté que les critères sont peu nombreux (entre deux et trois), formulés en des termes généraux qui semblent convenir ici à tous les types de problèmes additifs. Ces critères apparaissent faussement indépendants les uns des autres.
Dans le cas de réponses problématiques d’élève, quel que soit le type de problème additif, un jugement analytique qui engage une spécification des critères d’évaluation
Quand l’enseignant cherche à comprendre le raisonnement de l’élève, une erreur effectuée, etc., mais qu’il peine à y parvenir, nos analyses montrent que le jugement de l’enseignant est non seulement analytique, mais que celui-ci tend à engendrer une spécification des critères existants. Par exemple, l’enseignant se pose des questions telles que : Qu’est-ce qui est précisément considéré comme pertinent dans la démarche de l’élève ? Quelles imprécisions sont acceptables ? Quel niveau de maîtrise opératoire peut être exactement attendu ? Au contact de la singularité (imprévue) de la réponse de l’élève, l’enseignant tend à multiplier les critères d’évaluation, dépassant ainsi la formulation générale de ses critères préexistants. Des référents contextuels (Mottier Lopez, 2017) entrent aussi en ligne de compte, attachés au contrat didactique de la classe par exemple. Dans cette logique, l’évaluation se fait alors diagnostique avant d’être certificative. La majorité des enseignants de notre étude disent exploiter les informations ainsi produites pour envisager ensuite des régulations formatives ciblées.
Un des obstacles régulièrement observés dans ce dernier cas de figure consiste pour l’enseignant à « traduire » son jugement analytique, qui s’est spécifié, dans le cadre critérié prédéfini, compte tenu notamment de l’interdépendance des critères d’évaluation des RP - à titre de rappel, la réussite de l’un détermine la réussite de l’autre. Afin d’y faire face, cela demande une mise en tension constructive entre le jugement analytique opéré et un jugement holistique, c’est-à-dire amenant l’enseignant à appréhender les différentes dimensions de la RP de façon dynamique entre elles. Cela ne va pas sans poser des problèmes aux enseignants qui, ce faisant, doivent s’appuyer sur leur jugement professionnel (Allal, 2013) pour prendre des décisions qui nécessitent des adaptations (voire des compromis). À partir d’un cas problématique « résolu », celui-ci prend alors un statut de référent pour d’autres cas comparables. La référentialisation est ici à l’oeuvre en tant que « processus dynamique de co-constitution entre référés et référents ; foncièrement située, c’est-à-dire par rapport, et avec, des contextes significatifs agissant » (Mottier Lopez et Dechamboux, 2017, p. 16). Le sens spécifique du référent se construit dans une mise en relation interprétative avec le ou les référés sélectionnés, et inversement. Cette mise en relation référents-référés prend foncièrement sens aussi en fonction de contextes pluriels : notamment, les choix concertés dans un même établissement scolaire, les pratiques et normes sociales de chaque classe, le contrat didactique propre à l’objet de savoir en jeu, la situation même de correction, une copie singulière d’élève.
Dans notre étude, malgré l’observation de pratiques variées entre enseignants, les adaptations en jeu dans ce processus de référentialisation ont fréquemment été soumises à l’avis des collègues, en faveur de décisions concertées au sein d’un même établissement scolaire. Nous considérons que cette tension constructive (et complexe) entre jugement analytique (appréhension de chaque dimension de la RP – qui demanderait également une prise en compte de la particularité de chaque type de problème, ce que les enseignants font peu) et jugement holistique (mise en relation globale entre les dimensions interdépendantes analysées) représente certainement un des enjeux majeurs pour l’évaluation des compétences, dont celle de résoudre des problèmes de mathématiques, tant pour la recherche en éducation que pour la formation initiale et continue des enseignants.
Appendices
Annexe
Annexe 1. Objectifs d’apprentissage et contenus du Plan d’études romand portant sur la RP additifs (domaine « opérations ») pour les quatre années du cycle moyen (8-12 ans)
Remerciements
Nous remercions le Fonds national suisse de la recherche scientifique (FNS) et les enseignants qui ont accepté de participer à cette recherche. Nous remercions également Lionel Dechamboux, Sophie Serry et Walther Tessaro du groupe de recherche Évaluation, régulation et différenciation des apprentissages dans les systèmes d’enseignement (EReD).
Notes
-
[1]
Nous avons déjà analysé ce sujet dans un précédent article pour le contexte de la recherche présentée ici (Mottier Lopez, 2014).
-
[2]
En Suisse romande, le choix a été fait de parler de « moyens d’enseignement » plutôt que de manuels scolaires afin d’insister notamment sur l’idée de ressources mises à la disposition des enseignants. Voir : www.ciip.ch/Moyens-denseignement/Moyens-denseignement-romands-MER/Moyens-denseignement-romands-MER.
-
[3]
Nous parlerons désormais d’« évaluation certificative », qui a pour avantage de mieux nommer la fonction qu’elle vise, comparativement au terme historique d’« évaluation sommative » introduit par Scriven dans les années 1960.
-
[4]
Notre précédente analyse (Mottier Lopez, 2015) montre combien il s’agit d’une des grandes incompréhensions à propos de l’évaluation scolaire, qui a fait du tort à l’évaluation formative et aux réformes visant à promouvoir des évaluations certificatives sans note.
-
[5]
Le terme HarmoS fait référence à l’Accord intercantonal sur l’harmonisation de la scolarité obligatoire entre les différents cantons suisses et accompagne la nouvelle désignation des années d’études dans les cantons ayant approuvé ce texte. Voir www.edk.ch/dyn/11737.php. L’abréviation que nous utiliserons désormais pour désigner les années d’études sera PH (primaire harmonisé).
-
[6]
Cette étude fait partie d’une recherche de plus large envergure (Mottier et al., 2012), soutenue par le Fonds national suisse de la recherche scientifique (octroi n° 100013-143453/1).
-
[7]
Le groupe de recherche Évaluation, régulation et différenciation des apprentissages dans les systèmes d’enseignement (EReD). Voir www.unige.ch/fapse/ered.
-
[8]
Sciemment, nous utilisons le terme « exercice » dans cet article, également utilisé sur le terrain, car il permet de regrouper des consignes, des énoncés, des questions aux formes variées qui sollicitent des réponses longues à élaborer, des réponses courtes à rédiger, des réponses à sélectionner, etc., et qui peuvent également impliquer une ou plusieurs tâches à effectuer par les élèves au sein d’un même exercice.
-
[9]
Voir Mottier Lopez et Dechamboux (2017) pour une discussion théorique de ces catégories à des fins de modélisation du jugement évaluatif en acte de l’enseignant.
-
[10]
Voir également Tessaro, Dechamboux, Morales Villabona et Mottier Lopez (2016) pour une description de ces pratiques de collaboration.
-
[11]
Appelé également « fichet ». Il s’agit d’une table de spécification (ou champ de l’épreuve) simplifiée.
-
[12]
Voir cette recommandation au www.plandetudes.ch/mathematiques.
-
[13]
Depuis la rentrée scolaire de 2014, les enseignants du cycle moyen de l’école genevoise doivent attribuer des notes de 1,5 à 6,0 par tranche de demi-notes, et non plus par notes entières, comme c’était le cas au moment de notre recherche.
-
[14]
Par exemple : Pierre a 7 billes. Il joue une partie et en gagne 5. Combien a-t-il de billes ?
-
[15]
Par exemple : Pierre vient de perdre 5 billes. Il lui en reste maintenant 7. Combien de billes avait-il avant la partie ? D’une façon générale, les problèmes de « gains » sont plus facilement résolus que les problèmes de « pertes ». Dans ce cas précis, comme le relève Vergnaud, il est contre-intuitif d’ajouter des billes quand on les a perdues.
-
[16]
Après le prénom de l’enseignant figure le prénom de l’élève réduit à trois lettres.
-
[17]
Rares sont les critères indiqués dans l’entête de l’épreuve qui, quant à lui, signale plutôt les objectifs d’apprentissage.
-
[18]
Par exemple, dans un problème de recherche de l’état final par une addition, la somme obtenue est le nombre à reprendre dans la phrase-réponse, ce qui n’est pas le cas d’un problème de recherche d’une transformation négative résolue par une « addition à trou », dont la somme n’est pas la réponse pour la phrase-réponse.
Bibliographie
- Allal, L. (2008). Évaluation des apprentissages. Dans A. van Zanten (dir.), Dictionnaire de l’éducation (pp. 311-314). Paris : Presses universitaires de France.
- Allal, L. (2013). Teachers’ professional judgement in assessment: A cognitive act and a socially situated practice. Assessment in Education: Principles, Policy & Practice, 20, 20-34. doi: 10.1080/0969594X.2012.736364
- Amigues, R. et Zerbato-Poudou, M.-T. (1996). Les pratiques scolaires d’apprentissage et d’évaluation. Paris : Dunod.
- Anadón, M. et Guillemette, F. (2007). La recherche qualitative est-elle nécessairement inductive ? Recherches qualitatives, 5, 26-37. Repéré à www.recherche-qualitative.qc.ca/documents/files/revue/hors_serie/hors_serie_v5/anadon.pdf
- Antibi, A. (2003). La constante macabre ou comment a-t-on découragé des générations d’élèves. Toulouse : Math’adore.
- Barbier, J.-M. (1985). L’évaluation en formation. Paris : Presses universitaires de France.
- Bressoux, P. et Pansu, P. (2003). Quand les enseignants jugent leurs élèves. Paris : Presses universitaires de France.
- Brookhart, S. M. (2013). How to create and use rubrics for formative assessment and grading. Alexandria, VA: ASCD.
- Brousseau, G. (1986/1996). Fondements et méthodes de la didactique des mathématiques. Dans J. Brun (dir.), Didactique des mathématiques (pp. 45-143). Lausanne : Delachaux et Niestlé.
- Brun, J. et Schubauer-Leoni, M. L. (1981). Recherches sur l’activité de codage d’opérations additives en situation d’interaction sociale et de communication. Cahiers IMAG, Grenoble : Université de Grenoble.
- Charters, E. (2003). The use of think-aloud methods in qualitative research: An introduction to think-aloud methods. Brock Education, 12, 68-82. doi: 10.26522/brocked.v12i2.38
- Conne, F. (1984). Calculs numériques et calculs relationnels dans la résolution de problèmes d’arithmétique. Recherches en didactique des mathématiques, 5(3), 269-332.
- Crahay, M. (2009). Articuler l’évaluation en classe et le pilotage des systèmes, est-ce possible ? Dans L. Mottier Lopez et M. Crahay (dir.), Évaluations en tension : entre la régulation des apprentissages et le pilotage des systèmes (pp. 233-251). Bruxelles : De Boeck.
- Denzin, N. K. (1978). The research act: A theoretical introduction to sociological methods. New York: McGraw-Hill.
- De Ketele, J.-M. et Gerard, F.-M. (2005). La validation des épreuves d’évaluation selon l’approche par les compétences. Mesure et évaluation en éducation, 28(3), 1-26.
- De Vecchi, G. (2014). Évaluer sans dévaluer (2e éd.). Paris : Hachette Livre.
- Dierendonck, C., Loarer, E. et Rey, B. (dir.). (2013). L’évaluation des compétences en milieu scolaire et en milieu professionnel. Bruxelles : De Boeck.
- Duru-Bellat, M. (2003). Les inégalités sociales à l’école : genèse et mythes. Paris : Presses universitaires de France.
- Feyfant, A. (2015). La résolution de problèmes de mathématiques au primaire. Dossier de veille de l’IFÉ, 105. Repéré à https://f-origin.hypotheses.org/wp-content/blogs.dir/1857/files/2015/12/105-novembre-2015.pdf
- Figari, G. (1994). Évaluer : quel référentiel ? Bruxelles : De Boeck.
- Figari, G. et Remaud, D. (2014). Méthodologie d’évaluation en éducation et formation. Bruxelles : De Boeck.
- Gagnebin, A., Guignard, N. et Jaquet, F. (1997). Apprentissage et enseignement des mathématiques : commentaires didactiques sur les moyens d’enseignement pour les degrés 1 à 4 de l’école primaire. Neuchâtel : Institut de recherche et de documentation pédagogique.
- Gerard, F.-M. (2005, octobre). L’évaluation des compétences à travers des situations complexes. Actes du 18e Colloque de l’ADMEE-Europe, Reims. Repéré à www.fmgerard.be/textes/sitcomp.html
- Hadji, C. (2012). Faut-il avoir peur de l’évaluation ? Bruxelles : De Boeck.
- Issaieva, E. et Crahay, M. (2010). Conceptions de l’évaluation scolaire des élèves et des enseignants : validation d’échelles et étude de leurs relations. Mesure et évaluation en éducation, 33(1), 31-61. doi: 10.7202/1024925ar
- Jorro, A. (2016). Postures professionnelles des conseillers en évolution professionnelle. Revueinternationale de pédagogie de l’enseignement supérieur, 32(3), Repéré à http://ripes.revues.org/1131
- Lafortune, L. et Allal, L. (dir.). (2008). Jugement professionnel en évaluation : pratiques enseignantes au Québec et à Genève. Québec : Presses de l’Université du Québec.
- Loquet, M., Garnier, A. et Amade-Escot, C. (2002). Transmission des savoirs en activités physiques, sportives et artistiques dans des institutions différentes : enseignement scolaire, entraînement sportif, transmission chorégraphique. Revue française de pédagogie, 141, 99-109. doi: 10.3406/rfp.2002.2918
- Meirieu, P. (2009). La foi des mécréants (Préface). Dans O. Neumayer, M. Neumayer et E. Vellas (dir.), Relever les défis de l’Éducation nouvelle : 45 parcours d’avenir. Lyon : Chronique sociale. Repéré à www.meirieu.com/PREFACES/LIEN.htm
- Merle, P. (2007). Les notes : secrets de fabrication. Paris : Presses universitaires de France.
- Merle, P. (2012). L’évaluation des élèves : une modélisation interactionniste des pratiques professorales. Dans L. Mottier Lopez et G. Figari (dir.), Modélisations de l’évaluation en éducation : questionnements épistémologiques (pp. 81-96). Bruxelles : De Boeck.
- Mottier Lopez, L. (2008). Apprentissage situé : la microculture de classe en mathématiques. Berne : Peter Lang.
- Mottier Lopez, L. (2014). L’évaluation pédagogique va-t-elle enfin marcher sur ses deux pieds ? : les enseignements de l’histoire récente de l’école primaire genevoise. Éducation et francophonie, 42(3), 85-101. doi: 10.7202/1027407ar
- Mottier Lopez, L. (2015). L’évaluation formative des apprentissages des élèves : entre innovations, échecs et possibles renouveaux par des recherches participatives. Questions vives, 23. doi: 10.4000/questionsvives.1692
- Mottier Lopez, L. (2017). Une modélisation pour appréhender la référentialisation dans l’évaluation des apprentissages des élèves. Dans P. Detroz, M. Crahay et A. Fagnant (dir.), L’évaluation à la lumière des contextes et des disciplines (pp. 169-192). Bruxelles : De Boeck.
- Mottier Lopez, L. et Dechamboux, L. (2017). D’un référentiel d’évaluation fixe à une co-constitution référentielle dynamique : ce que nous apprend le jugement situé de l’enseignant. Contextes et didactiques, 9, 12-29. Repéré à https://archive-ouverte.unige.ch/unige:96405
- Mottier Lopez, L. et Laveault, D. (2008). L’évaluation des apprentissages en contexte scolaire : développements, enjeux et controverses. Mesure et évaluation en éducation, 31(3), 5-34. doi: 10.7202/1024962ar
- Mottier Lopez, L., Tessaro, W., Dechamboux, L. et Morales Villabona, F. (2012). La modération sociale : un dispositif soutenant l’émergence de savoirs négociés sur l’évaluation certificative des apprentissages des élèves. Questions vives, 6(18), 159-175. doi: 10.4000/questionsvives.1235
- Neumayer, M. et Vellas, E. (dir.). (2015). Évaluer sans noter, éduquer sans exclure. Lyon : Chronique sociale.
- Noizet, G. et Caverni, J.-P. (1972). Psychologie de l’évaluation scolaire. Paris : Presses universitaires de France.
- Perrenoud, P. (1984). La fabrication de l’excellence scolaire. Genève : Droz.
- République et canton de Genève (2012). Document de liaison – Enseignement et évaluation, cycle moyen : guide pratique à l’attention des enseignants. Genève : Département de l’instruction publique, de la culture et du sport.
- Rey, B., Carette, V., Defrance, A. et Kahn, S. (2003). Les compétences à l’école : apprentissage et évaluation. Bruxelles : De Boeck.
- Tardif, J. (2006). L’évaluation des compétences : documenter le parcours de développement. Montréal : Chenelière Éducation.
- Tessaro, W., Dechamboux, L., Morales Villabona, F. et Mottier Lopez, L. (2016). La modération sociale pour se former à l’évaluation des apprentissages. Éducation permanente, 208(3), 65-76.
- Vergnaud, G. (1981). L’enfant, la mathématique et la réalité. Berne : Peter Lang.
- Vergnaud G. (1982). A classification of cognitive tasks and operations of thought involved in addition and subtraction problems. ln T. P. Carpentier, J. M. Moser, & T. Romberg (Eds.), Addition and subtraction: Acognitive perspective (pp. 39-59). Hillsdale, NJ: Lawrence Erlbaum.
- Vergnaud, G. (1987). Les fonctions de l’action et de la symbolisation dans la formation des connaissances chez l’enfant. Dans J.-P. Bronckart, P. Mounoud et J. Piaget (dir.), Psychologie (pp. 821-844). Paris : La Pléiade.
- Vergnaud, G. et Durand, C. (1976). Structures additives et complexité psycho- génétique. Revue française de pédagogie, 36, 28-43. doi: 10.3406/rfp.1976.1622
List of figures
Figure 1
Catégories qui caractérisent l’activité évaluative et unités étudiées
List of tables
Tableau 1
Composition des contrôles écrits et part prise par les exercices de résolution de problèmes
Tableau 2
Catégorisation des RP en 5PH selon la typologie de Vergnaud



 10.7202/1024925ar
10.7202/1024925ar