Résumés
Résumé
Dans cette étude, j’analyse les raisons qui expliquent pourquoi le taux d’abandon scolaire québécois est plus élevé que la moyenne nationale et, en particulier, beaucoup plus élevé qu’en Ontario (la province auquelle le Québec se compare tout naturellement). Le modèle économétrique est construit autour de groupes de trois facteurs fondamentaux ; le niveau d’éducation des parents et / ou d’autres caractéristiques familiales, le sexe ainsi que l’hétérogénéité non observée et permet de déterminer jusqu’à quel point le différentiel positif entre le Québec et l’Ontario est d’un niveau normalement attendu, étant donné d’une part les différences de richesse entre les deux provinces et d’autre part la forte corrélation entre l’éducation des parents et des enfants (mesurée dans beaucoup de pays). Les résultats indiquent qu’au Québec, tout comme en Ontario, l’incidence de l’abandon scolaire décroît avec le niveau d’éducation des parents et est moins élevé chez ceux qui ont été élevés dans une famille unie. Au Québec, et contrairement à l’Ontario, l’incidence de l’abandon scolaire est beaucoup plus élevée chez les garçons. Le plus haut taux d’abandon scolaire chez les garçons semble indépendant de la composition familiale. Une analyse des salaires et revenus des jeunes décrocheurs semblent indiquer qu’ils ne sont pas pénalisés lorsqu’on les compare avec ceux qui sont entrés sur le marché du travail après avoir complété leur secondaire. Il semble donc que le faible taux de rendement associé à la diplômation, combiné au niveau relativement élevé du salaire minimum québécois, contribuent à maintenir le taux de décrochage québécois à un niveau particulièrement élevé.
Abstract
In this paper, I investigate the Quebec-Ontario school drop-out rate differential using a dynamic model of schooling attainment. The model stresses three distinct set of factors, parental education (or other family background variables), gender differences and unobserved (to the econometrician) factors. In both Quebec and Ontario, the school drop out rate is found to decrease with parental education. However, the male-female differential in the incidence of school drop-out in Quebec is much higher than it is in Ontario. Furthermore, this higher incidence is not explained by interactions between gender and family background. Finally, an econometric analysis of post schooling wages indicates that, when compared to those who have completed high school only, school drop outs are not penalized for dropping out.
Corps de l’article
Introduction
Cette étude a pour but de procéder à une analyse comparative du comportement des jeunes étudiants québécois et ontariens au niveau de l’abandon scolaire. Il est bien connu que l’abandon scolaire (ou décrochage scolaire) en bas âge est un problème sérieux auquel doit faire face l’économie canadienne. Bien qu’il soit quelquefois difficile de quantifier précisément l’incidence de l’abandon scolaire, il est souvent avancé que de 15 % à 20 % des jeunes Canadiens ne terminent pas leurs études de niveau secondaire[1]. Bien évidemment, l’incidence de l’abandon scolaire est susceptible de varier significativement d’une génération à l’autre.
Au Canada, l’incidence de l’abandon scolaire varie également beaucoup d’une région à l’autre et il semble particulièrement aigü au Québec. Par exemple, le taux d’abandon scolaire québécois est plus élevé que la moyenne nationale et, en particulier, beaucoup plus élevé qu’en Ontario (la province auquelle le Québec se compare tout naturellement en termes économiques). Cela en dépit du fait que la complétion des études secondaires requérait, jusqu’à tout récemment, 13 années d’études en Ontario et 11 au Québec. Cela représente un défi majeur pour ceux qui élaborent les politiques sociales et économiques au Québec. De plus, les analystes québécois ont récemment noté que le taux d’abandon scolaire des jeunes hommes et jeunes garçons apparait anormalement plus élevé que celui des jeunes Québécoises[2].
Depuis quelques années, un nombre important d’études consacrées aux facteurs déterminants du niveau de scolarité atteint par les individus ont permis de mettre en lumière le rôle primordial des antécédants familiaux. En particulier, la corrélation positive entre le niveau de scolarité des parents et celui des enfants a été vérifiée à partir de simples corrélations (Kane, 1994), dans le cadre de modèles dynamiques de forme réduite (Cameron et Heckman, 1998 et 2001) et, également, dans le cadre de modèles dynamiques structurels (Keane et Wolpin, 1997; Eckstein et Wolpin, 1999; Belzil et Hansen, 2002 et 2003).
Globalement, l’ensemble des études basées sur des modèles dynamiques tendent également à démontrer l’importance de l’hétérogénéité non observée. Cette hétérogénéité peut représenter des facteurs tels que l’habileté académique, la motivation, le goût pour les études, le taux de préférence intertemporel ou tout autre trait individuel qui demeure constant dans le temps. Il est à noter que la forte corrélation intergénérationnelle au niveau de l’éducation peut s’expliquer par plusieurs facteurs structurels. Les familles plus aisées (dont les membres tendent à être plus éduqués que la moyenne) peuvent avoir tendance à donner une aide financière plus généreuse à leurs enfants. Cette aide financière se traduit par une réduction des coûts d’opportunité liés à l’obtention d’un plus haut niveau de scolarité. Également, une large partie de l’habileté individuelle peut être expliquée par des facteurs génétiques ou, plus simplement par le temps dévoué par les parents à l’éducation et à la formation de l’enfant. Bien que la plupart des résultats statistiques mentionnés précédemment soient obtenus à partir de données américaines, il apparait certain que des conclusions similaires peuvent être tirées pour le Canada et pour le Québec.
Fondamentalement, un différentiel positif au niveau de l’incidence de l’abandon scolaire entre le Québec et l’Ontario n’a donc rien d’étonnant. L’Ontario est une économie plus riche où le niveau de scolarité est aussi plus élevé. Par conséquent, la forte corrélation intergénérationnelle (de signe positif) au niveau de l’éducation incite à croire que les jeunes Québécois devraient donc obtenir un niveau de scolarité inférieur à celui des jeunes Ontariens.
En plus des différences au niveau de l’éducation des parents et au niveau de la richesse globale, d’autres facteurs peuvent expliquer ce différentiel positif. Il est bien connu que les taux marginaux d’impôts sont plus élevés au Québec qu’en Ontario. Cette différence tend à réduire les rendements en éducation, en particulier pour les emplois rémunérateurs requérant un plus haut niveau de scolarité, et peut donc expliquer le plus faible niveau de scolarité. De façon générale, il est bien clair que la décision d’investir en éducation est positivement corrélée avec ces même rendements (Dagenais, Montmarquette et Viennot-Briot, 2001). Il est aussi important de noter que le salaire minimum québécois est plus élevé que le salaire minimum ontarien. Sur la période d’analyse économétrique couverte par l’étude qui suit, le salaire minimum québécois était d’environ 10 % plus élevé qu’en Ontario. Cette caractéristique crée une certaine compression des salaires entre les emplois requérant un faible niveau de formation et tend aussi à réduire les rendements en éducation. En clair, cela peut donc inciter les jeunes Québécois à abandonner leurs études en plus grand nombre.
Jusqu’à quel point le différentiel positif entre le Québec et l’Ontario est d’un niveau normalement attendu, étant donné les différences de richesse entre les deux provinces, est donc une question fondamentale auquelle il faut répondre pour pouvoir comprendre le phénomène de l’abandon scolaire.
L’analyse proposée dans cette recherche est basée sur un modèle économétrique de type dynamique où la progression d’un niveau de scolarité au suivant est représentée par une fonction de hasard. Bien que ce modèle soit de forme réduite, il peut aussi admettre une représentation plus structurelle; c’est-à-dire qu’il est basé sur la différence entre l’utilité associée à l’abandon scolaire (pour entrer sur le marché du travail) et l’utilité associée à la continuation des études. Le modèle est construit autour de groupes de trois facteurs fondamentaux; le niveau d’éducation des parents et / ou d’autres caractéristiques familiales, le sexe et l’hétérogénéité non observée.
Les objectifs de cette recherche sont multiples. Premièrement, mon intention est de mesurer l’importance relative des facteurs suivants dans la détermination du niveau de scolarité; niveau de capital humain des parents (c’est-à-dire le niveau d’éducation), le sexe et les facteurs individuels non observables.
Le second objectif est de déterminer la cause principale du différentiel Québec-Ontario. Plus précisément, il est de distinguer entre les deux hypothèses suivantes; i) le différentiel entre le Québec et l’Ontario est simplement expliqué par la différence au niveau de la scolarité des parents, ii) le différentiel Québec-Ontario est principalement expliqué par des différences de comportements (principalement entre les jeunes garçons ontariens et québécois).
Le troisième objectif est de simuler le taux d’abandon scolaire sous divers scénarios. Plus particulièrement, je tenterai de répondre à certaines questions. Quelle serait l’incidence de l’abandon scolaire observé au Québec si les parents québécois jouissaient du même niveau de scolarité que les parents ontariens? Quelle serait l’incidence de l’abandon scolaire observé au Québec si les jeunes Québécois avaient un comportement similaire aux jeunes Québécoises?
Le quatrième objectif est de comparer les performances sur le marché du travail des jeunes décrocheurs avec celles des jeunes qui ont complété leurs études secondaires et sont tout de suite entrés sur le marché du travail. Cette comparaison se fait à l’aide de données sur le salaire hebdomadaire obtenu en 1995. En fait, cet objectif est grandement relié à la connaissance des rendements en éducation.
Finalement, un cinquième objectif est d’ébaucher un ensemble de politiques qui puissent réduire le taux de décrochage scolaire au Québec.
Les résultats majeurs de cette étude sont au nombre de trois. Premièrement, il appert que l’éducation des parents est, de loin, le facteur le plus important expliquant le niveau de scolarité. Par exemple, au Québec, 42 % de la variation totale au niveau de la scolarité est expliquée par l’éducation des parents alors que celle-ci explique près de 55 % de la variation totale en Ontario. Deuxièmement, près de 10 % de la variance totale est expliquée par la différence de comportements entre garçons et filles. Ce résultat peut sembler troublant. En effet, en Ontario, les différences entre garçons et filles ne contribuent presque pas à la variation totale (moins de 1 %). Troisièmement, une analyse des salaires et revenus des jeunes décrocheurs semblent indiquer qu’ils ne sont pas pénalisés lorsqu’on les compare avec ceux qui ont investi le marché du travail après avoir complété leur secondaire. Il semble donc que le faible taux de rendement associé à la diplômation, combiné au niveau relativement élevé du salaire minimum québécois, contribuent à maintenir le taux de décrochage québécois à un niveau particulièrement élevé.
1. L’Enquête de Statistique Canada auprès des sortants
L’analyse présentée dans cette recherche est basée sur l’Enquête de Statistique Canada auprès des sortants. Cette enquête renferme des informations sur la scolarité et les expériences de travail (heures de travail, revenu, formation en entreprise, etc.) de plus de 9 000 Canadiens âgés entre 18 et 20 ans en 1990. Pour des raisons de représentativité géographique, les individus vivant dans des zones à très faible densité de population ont été suréchantillonnés. En 1995, le ministère canadien des Ressources humaines a demandé à Statistique Canada d’interviewer de nouveau les mêmes individus. Un taux de réponse d’environ 67 % a permis de construire un échantillon de 6 284 jeunes individus. Au moment de la deuxième interview, les répondants étaient âgés, entre 22 et 24 ans. Après l’élimination des observations erronées, nous nous retrouvons avec un échantillon de 968 jeunes Québécois et de 1 088 jeunes Ontariens[3].
Le contenu de l’Enquête auprès des sortants est assez large. Outre des informations sur les expériences de travail et les expériences académiques, on y retrouve des informations sur l’abandon scolaire ainsi que de multiples informations sur l’environnement familial. Par exemple, il est possible de connaitre le niveau de scolarité du père et de la mère (cette variable est définie par catégories) et, également, de savoir si le jeune individu a été élevé par ses deux parents naturels[4]. Cet ensemble de variables se rapproche beaucoup des variables disponibles dans le NLSY (National Longitudinal Survey of Youths)[5]. Quelques statistiques descriptives se retrouvent au tableau 1.
Tableau 1
Quelques statistiques descriptives
Une inspection rapide des tableaux 2A et 2B révèle clairement le différentiel positif entre le Québec et l’Ontario au niveau du décrochage scolaire. En 1995, environ 18 % des jeunes Québécois avaient obtenu 10 années de scolarité ou moins tandis que seulement 9,9 % des jeunes Ontariens avaient obtenu 11 années ou moins. On note aussi que de facon générale, l’incidence de l’abandon scolaire est beaucoup plus élevé chez les garçons que chez les filles. Cela est particulièrement vrai pour le Québec où seulement 13 % des jeunes Québécoises n’avaient pas complété leurs études secondaires (contre 23 % des jeunes Québécois). En Ontario, 12,1 % des jeunes Ontariens n’avaient pas complété leurs études secondaires tandis que seulement 7,7 % des jeunes Ontariennes avaient abandonné leurs études avant la fin du secondaire.
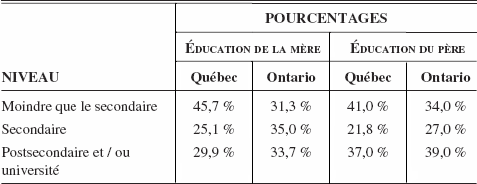
Si la différence entre les jeunes Québécois et les jeunes Ontariens est notable, la différence entre les parents ontariens et québécois est elle aussi très marquée. Plus de 46 % des jeunes Québécois ont répondu que leur mère n’avait pas terminé ses études secondaires tandis que 41 % ont répondu que leur père n’avait pas terminé le niveau secondaire. Pour l’Ontario, les pourcentages équivalents sont de 31 % (pour les mères) et 33,9 % (pour les pères).
Tableau 2
A
Niveaux de scolarité au Québec et en Ontario en 1995
B
Niveau de scolarité des parents au Québec et en Ontario
2. Modèle économétrique et méthode d’estimation
2.1 Description du modèle
L’analyse proposée dans cette recherche est basée sur un modèle économétrique de type dynamique où la progression d’un niveau de scolarité au suivant est représentée par une fonction de hasard. Bien que ce modèle soit de forme réduite, ce même modèle peut aussi admettre une représentation plus structurelle. Cela est possible lorsque le chercheur fait l’hypothèse que la variable latente sous-jacente au modèle est linéaire dans ses arguments et représente une utilité intertemporelle telle qu’une équation de Bellman[6]. Le modèle est construit autour de groupes de trois facteurs fondamentaux; le niveau d’éducation des parents et / ou d’autres caractéristiques familiales, le sexe et l’hétérogénéité non observée. La probabilité d’abandon scolaire après avoir complété E années de scolarité dénotée par HE, i, se lit comme suit
où le terme αE, i représente un terme spécifique à l’individu i et au niveau de scolarité E et où Xi est un vecteur de variables telles que l’éducation des parents ou autres caractéristiques familiales. Ce vecteur est orthogonal (par construction) au terme αe, i. Cela implique que la probabilité conditionnelle de transiter d’un niveau de scolarité (E) au suivant (E + 1) est égale à (1 – H(.)). Il est à noter, que pour cette raison, un signe positif pour un paramètre associé à une des variables devra être interprété comme un effet négatif de cette même variable sur le niveau de scolarité.
Je fais aussi l’hypothèse que
et que θi suit une loi inconnue mais qui peut être approximée par une distribution à valeurs discrètes avec deux points de support. Cette approche est équivalente à l’estimation de deux ensembles de termes constants propres à chaque niveau d’études avec la contrainte supplémentaire que la différence entre les deux termes constants à un niveau d’étude particulier est la même à chaque niveau d’études.
Si l’on définit Eg comme le nombre d’années d’étude requises pour obtenir un diplôme secondaire et Si comme le nombre d’années d’études complétées en 1995, la probabilité de compléter ses études secondaires, Pr(Si ≥ Eg ∣ Xi), est donnée par l’expression suivante
où le terme ![]() dénote la probabilité d’abandon scolaire pour l’individu i. À partir des estimés de la répartition de la population entre le type 1 et le type 2, il est facile de générer un échantillon de probabilités individuelles d’abandon scolaire
dénote la probabilité d’abandon scolaire pour l’individu i. À partir des estimés de la répartition de la population entre le type 1 et le type 2, il est facile de générer un échantillon de probabilités individuelles d’abandon scolaire ![]() , qui, par la suite, pourra etre utilisé afin de décomposer la variance totale en différentes composantes qui suscitent un intérêt particulier. Afin de faire cette décomposition, j’utilise le log odd’s ratio, (ψi(Xi, θi)) , qui peut s’exprimer comme suit
, qui, par la suite, pourra etre utilisé afin de décomposer la variance totale en différentes composantes qui suscitent un intérêt particulier. Afin de faire cette décomposition, j’utilise le log odd’s ratio, (ψi(Xi, θi)) , qui peut s’exprimer comme suit
où G(Xi, θi) représente une fonction de régression qui pourra être estimée avec un haut niveau de flexibilité. À partir de cet échantillon, il sera facile de décomposer la variance totale de G(.) en deux sources orthogonales (Xi et θi).
2.2 La fonction de vraisemblance
La fonction de vraisemblance, L(.), est construite comme suit. Il y a deux composantes principales; la probabilité de compléter t années de scolarité, Pr(T = t), et la probabilité d’observer le logarithme du salaire hebdomadaire (ou horaire) en 1995 égal a wi,1995. Les deux composantes s’écrivent comme suit
Pr(Ti = t ∣ θ) = πt-1s=1 (1 – Hi(s ∣ θ)) .Hi(t ∣ θ) où H(. ∣ θ) représente la probabilité conditionnelle d’abandon définie dans la section étant donné θ,
Pr(ln Wit = wit ∣ θ)
La fonction de vraisemblance finale est donnée par l’expression suivante :
où H(θ) représente la fonction de répartition de θ et Θ représente l’espace de toutes les valeurs possibles pour le terme θ. En pratique, puisque la fonction H(θ) est approximée par une loi discrète avec deux points de support, la fonction de vraisemblance à être maximisée est donc la suivante
3. Définition des variables utilisées
La variable contenant l’information sur le niveau de scolarité est construite à partir d’informations collectées en 1995. La question étant « Quel est le niveau de scolarité le plus élevé que vous ayez atteint en 1995? ». Comme très peu d’individus avaient terminé un degré universitaire en 1995, je modélise l’accession à la 12e année en Ontario et au niveau collégial au Québec. Étant donné que le niveau le plus bas rapporté est la 6e année, je considère que la 7e année est la première transition possible dans le modèle économétrique.
La variable contenant l’information sur la scolarité des parents est construite à partir de la classification suivante. Ceux qui ont obtenu moins de neuf années de scolarité, ceux qui ont obtenu moins que le nombre d’années requises pour un diplôme secondaire, ceux qui sont diplômés du secondaire et ceux qui ont fait des études postsecondaires (collège, université ou autre)[7].
La variable reflétant la composition familiale est égale à 1 si le répondant déclare avoir été élevé par son père et sa mère et 0 pour tous les autres cas possibles. L’information sur l’adoption provient d’une question libellée comme suit; avez-vous été adopté? L’âge au moment de l’adoption est cependant inconnue.
La langue principale est déterminée à partir de la question suivante : « Quelle langue utilisez-vous de façon la plus courante? »
La variable « urbaine » est déterminée selon la définition utilisée dans le recensement de 1986 et est égale à 1 pour ceux qui habitent une zone urbaine et 0 sinon.
La variable « Canadien » est égale à 1 pour ceux qui répondent être nés au Canada et 0 sinon.
4. Quels sont les déterminants principaux du niveau de scolarité des individus?
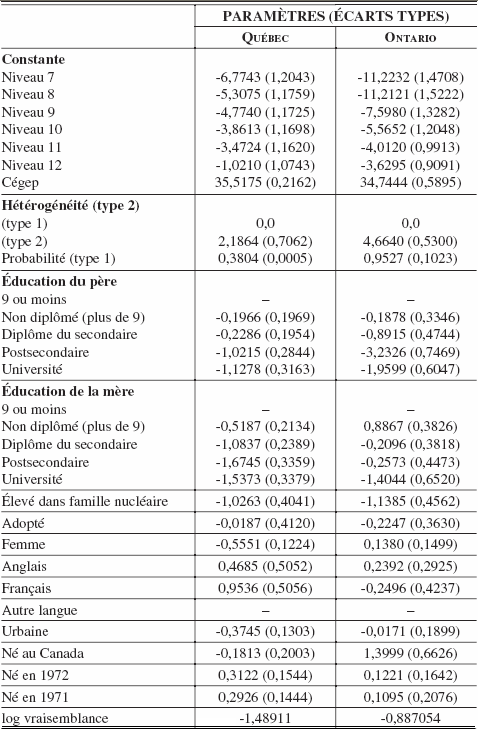
Dans un premier temps, j’ai estimé le modèle économétrique incluant toutes les variables explicatives possibles. Les résultats détaillés des paramètres estimés se retrouvent dans le tableau 3. De façon succincte, nous présenterons ensuite les plus notables.
Tableau 3
Paramètres estimés par maximum de vraisemblance
Premièrement, et tel qu’attendu, on retrouve une corrélation positive entre le niveau de scolarité des parents et la probabilité de transiter d’un niveau d’études au suivant. Cela est illustré par les paramètres négatifs associés aux différents niveaux d’éducation et par le fait qu’ils augmentent en valeur absolue avec le niveau d’étude des parents (le groupe de référence étant ceux qui ont moins de neuf années de scolarité). Il est particulièrment intéressant de noter que, au Québec et en Ontario, ceux qui ont été élevés dans une famille où le père et la mère étaient présents ont tendance à atteindre un niveau de scolarité plus élevé. Ce résultat en confirme d’autres obtenus avec des données américaines (en particulier le NLSY)[8].
Une des distinctions les plus importantes entre les paramètres estimés pour le Québec et l’Ontario se retrouve au niveau de l’hétérogénéite non observée. Bien qu’elle joue un rôle important pour le Québec, elle apparaît de moindre importance pour l’Ontario. Dans les deux cas, la valeur positive obtenue pour θ2 (2,19 pour le Québec et 4,66 pour l’Ontario) indique que les individus de type 2 sont dotés d’un taux de sortie plus élevé et obtiennent donc un niveau de scolarité plus bas que les individus de type 1. Les fractions estimées de la population appartenant au type 1 et au type 2 sont égales à 0,38 et 0,62 pour le Québec et à 0,96 et 0,04 respectivement pour l’Ontario. En pratique, ceci implique une plus petite variance du terme d’hétérogénéité non observée pour l’Ontario.
Les différences entre le Québec et l’Ontario ne s’arrêtent pas seulement au niveau de l’hétérogénéité non observable. Il y a aussi d’autres distinctions importantes entre les deux provinces et, en particulier, au niveau des différences de comportements entre garçons et filles.
La valeur du paramètre estimé pour les jeunes Québécoises (-0,5551) implique un taux de sortie beaucoup plus bas pour les filles et, ainsi donc, une plus faible proportion d’abandon scolaire chez les jeunes filles que chez les garçons. Il est très intéressant de noter que pour l’Ontario, on ne retrouve aucune différence significative entre les jeunes filles et les jeunes garçons. Le paramètre capturant la différence entre garçons et filles (0,1380) est non significativement différent de 0. De toute évidence, les différences de comportement entre jeunes hommes ontariens et québécois sont une source importante pouvant expliquer le différentiel Québec-Ontario au niveau de l’abandon scolaire. Les résultats indiquent aussi que c’est parmi les jeunes francophones que le taux d’abandon scolaire sera le plus élevé. En effet, le paramètre associé à la variable « Français » est positif (0,9536) et significatif et est deux fois plus élevé que chez les anglophones. Finalement, les autres variables ne semblent avoir qu’un impact mineur tant au Québec qu’en Ontario. Elles ne seront donc pas discutées.
5. La différence entre garçons et filles dépend-elle de la composition familiale?
Dans le présent contexte, il est naturel de se demander si la différence au niveau du décrochage entre hommes et femmes est elle-même amplifiée par la présence (ou l’absence) des deux parents. Après tout, il est possible que le plus haut taux d’abandon scolaire soit la résultat d’un plus haut taux d’inadaptation des garçons aux divers problèmes familiaux (divorce ou autres).
Pour répondre à cette question, il suffit de modéliser l’interaction entre sexe et composition familiale à l’aide de quatre variables binaires différentes représentant les quatres cas possibles. Ces quatres groupes sont les suivants : fille / famille nucléaire, fille / famille divisée, garçon / famille nucléaire et garçon / famille divisée. J’ai donc de nouveau estimé le même modèle en traitant le groupe fille / famille nucléaire comme étant le groupe de référence.
Les résultats, se retrouvant au tableau 4, indiquent clairement l’absence d’interaction significative. Bien que les paramètres (positifs) indiquent qu’en moyenne, tous les groupes ont un taux d’abandon plus élevé que le groupe de référence (les filles ayant été élevées dans une famille unie), le haut niveau des écarts types indiquent qu’il est impossible de différencier ces quatres groupes de façon significative. Ceci peut être simplement expliqué par la composition familiale uniforme qui affecte les garçons et les filles de manière à peu près égale.
En conclusion, le plus haut taux d’abandon scolaire chez les garçons semble indépendant de la composition familiale. Le problème est donc tout aussi « scolaire » que « familial ».
Tableau 4
Modèle avec interaction entre sexe et composition familiale – paramètres estimés par maximum de vraisemblance
6. Quelle est l’importance relative de l’éducation des parents et des autres variables?
À ce stade-ci, il serait important de quantifier l’importance relative des facteurs qui ont été identifiés. Pour ce faire, je vais donc me concentrer sur l’éducation des parents, le sexe et l’ensemble de tous les autres facteurs.
À l’aide de simulations qui reflètent la distribution des facteurs non observables, il est relativement facile de prédire les probabilités individuelles d’abandon scolaire (les ![]() ). Après avoir transformé ces mêmes
). Après avoir transformé ces mêmes ![]() en odds ratio (les ψi(Xi, θi)), il est possible d’en décomposer la variance totale en trois contributions distinctes (l’éducation des parents, le sexe et l’ensemble de tous les autres facteurs).
en odds ratio (les ψi(Xi, θi)), il est possible d’en décomposer la variance totale en trois contributions distinctes (l’éducation des parents, le sexe et l’ensemble de tous les autres facteurs).
Les résultats se retrouvent au tableau 5 et doivent se lire comme suit : les pourcentages représentent la fraction de la variation totale expliquée par le modèle économétrique et attribuable à chaque facteur (ou groupe de facteurs) particulier. Également au Québec, 42 % de la variation totale est expliquée par l’éducation des parents tandis qu’environ 49 % est expliquée par l’ensemble des autres facteurs. Près de 10 % de la variance totale est expliquée par la différence de comportements entre garçons et filles. Ce résultat peut sembler troublant puisqu’en Ontario les différences entre garçons et filles ne contribuent presque pas à la variation totale (moins de 1 %) alors que l’éducation des parents explique près de 55 %.
Tableau 5
Importance relative des variables explicatives
7. Quelques prévisions sur le niveau de décrochage scolaire
Les principaux résultats qui ont été analysés jusqu’à maintenant soulèvent au moins deux questions fondamentales :
Quelle serait l’incidence de l’abandon scolaire observé au Québec si les parents québécois jouissaient du même niveau de scolarité que les parents ontariens?
Quelle serait l’incidence de l’abandon scolaire observé au Québec si les jeunes Québécois avaient un comportement similaire aux jeunes Québécoises?
Les résultats de ces simulations se retrouvent au tableau 6. Pour chacun de ces deux scénarios, j’ai calculé un changement moyen au niveau de la probabilité individuelle d’abandon scolaire. Les nombres qui se retouvent dans ce tableau représentent donc une estimation du changement en pourcentage de la population des jeunes Québécois qui seront susceptibles d’abandonner l’école.
Tableau 6
Changements dans les taux moyens de décrochage scolaire sous divers scénarios
Dans les deux cas qui nous intéressent, il est évident que ces changements purement hypothétiques se traduisent par une baisse significative de l’incidence de l’abandon scolaire. Pour se faire une idée plus précise, on peut soustraire ces deux pourcentages du pourcentage d’abandon scolaire estimé pour le Québec dans l’enquête sur les sortants (environ 18 %).
8. L’ajustement sur le marché du travail des jeunes décrocheurs
À ce stade de la recherche, il est naturel de se demander si les jeunes décrocheurs éprouvent des difficultés particulières sur le marché du travail si on les compare à ceux qui ont cessé l’école après avoir obtenu leur diplôme secondaire. Pour répondre à cette question, j’ai estimé de nouveau le modèle économétrique auquel j’ai adjoint la densité des revenus hebdomadaires dans l’emploi de référence occupé en 1995. La spécification de la densité des salaires / revenus est très classique. Elle est basée sur une fonction de régression pour le logarithme des revenus qui contient le niveau de scolarité, deux indicateurs égaux à un si le père et la mère ont fait des études postsecondaires ainsi que le terme d’hétérogénéité non observé, identifié dans la fonction de transition d’un niveau de scolarité à l’autre. Pour atteindre le plus haut niveau de flexibilité possible, l’effet d’une année de scolarité varie d’un niveau à l’autre à l’aide d’une variable binaire pour chaque niveau de scolarité. Il est donc particulièrement aisé de tester l’homogénéité des offres de salaires faites aux décrocheurs et aux diplômés du secondaire. Comme le nombre exact d’années de scolarité est difficile à obtenir pour ceux qui ont fait des études postsecondaires, j’ai groupé ceux-ci dans un seul niveau. De plus, un grand nombre de jeunes n’ayant pas pas encore complété leurs études, le groupe composé de ceux qui ont eu accès au cégep ou à l’université ne suscite pas d’intérêt immédiat. Cela est sans conséquence grave car le principal objectif de cette étude est de comparer les décrocheurs à ceux qui ont terminé leur secondaire. Cette fonction est la suivante :
Les variables sont définies comme suit :
ln wi,1995 représente le logarithme des salaires (ou des revenus hebdomadaires) dans l’emploi de référence le plus récent;
les variables Ind10, Ind11, et Indpostsec sont des variables binaires indiquant le niveau de scolarité atteint (9 années ou moins, 10 années, 11 années ou niveau postsecondaire). Les paramètres δ1, δ2, δ3 et δ4 représentent les rendements à l’éducation. Le groupe de référence est donc celui contenant les jeunes ayant obtenu neuf années ou moins de scolarité;
les variables mothed et fathed sont des variables binaires indiquant si le père et la mère ont fait des études postsecondaires;
les variables âge19 et âge20 sont des variables binaires correspondant aux individus de 19 ans et de 20 ans respectivement (le groupe de référence est composé de ceux de 18 ans);
le terme θi, déjà introduit dans la deuxième section, est inclus dans la régression afin d’admettre la possibilité que l’hétérogénéité non observée affectant le niveau de scolarité soit correlé avec l’habileté (non observée) sur le marché du travail;
le terme εi,t représente un terme purement aléatoire suivant une loi normale centrée à 0 avec variance σw2.
Les résultats sont assez éloquents. Il est clair que les paramètres estimés peuvent être utilisés afin de retrouver les effets marginaux d’une année supplémentaire de scolarité propre à chaque niveau. Ces effets marginaux se retrouvent au tableau 7. J’ai considéré deux cas. Dans le premier cas (1re colonne), je fais une distinction entre les décrocheurs qui ont obtenu 10 années de scolarité et ceux qui ont obtenu 9 années ou moins. Dans le second (2e colonne), j’ai groupé tous les décrocheurs en un seul groupe. Les résultats indiquent que le fait de compléter son secondaire n’a pas d’effet causal positif sur les gains hebdomadaires. Les estimés pour δ2 et δ3 (1re colonne) ne sont pas significativement différents de 0. Dans la 2e colonne, la valeur du paramètre estimé pour δ3 (-0,0164) indique que ceux qui travaillent avec un diplôme du secondaire gagnent 1,6 % de moins que les décrocheurs. Cependant, encore une fois, le haut niveau de l’écart type indique le paramètre est non significativement différent de 0. En d’autres termes, les gains hebdomadaires des diplômés du secondaire ne dépassent pas ceux des décrocheurs.
Tableau 7
Rendements en éducation (revenus hebdomadaires)
Note : Les rendements sont calculés à l’aide des valeurs de la fonction spline qui a été préalablement estimée.
Il est intéressant de noter que, contrairement à la scolarité, les revenus augmentent avec l’âge. Pour ces jeunes décrocheurs et ces jeunes gradués, l’expérience sur le marché du travail semble plus valorisée que la scolarite. Les autres paramètres indiquent que les jeunes femmes gagnent moins que les jeunes hommes. Ceci peut être explicable par le fait qu’une grande partie des emplois disponibles pour les jeunes décrocheurs sont fort probablement dans des emplois requérant des efforts physiques ou des emplois au salaire minimum. Il semble donc que le faible taux de rendement associé à un diplôme, combiné au niveau relativement élevé du salaire minimum québécois, contribuent à maintenir le taux de décrochage québécois particulièrement élevé.
Conclusion
La littérature économique sur les modèles structurels de comportement (voir Eckstein et Wolpin, 1999; Keane et Wolpin, 1997 ainsi que Belzil et Hansen, 2002) ainsi que celle sur les modèles dynamiques de forme réduite nous enseignent le rôle important des goûts et habiletés individuelles dans le choix des carrières. En particulier, il est bon de constater que les choix individuels sont, dans une large mesure, dictés par des impératifs non pécuniaires et que, ces mêmes goûts et habiletés sont largement corrélés avec l’éducation des parents. Au niveau anecdotique, cela peut se traduire par le fait que beaucoup d’étudiants ayant accès à des professions / occupations payantes, vont quelquefois choisir de s’investir dans des professions moins rémunératrices mais plus prestigieuses (et requérant un plus haut niveau de scolarité) ou, à l’inverse, qu’un certain nombre d’étudiants ayant accès aux études supérieures décident de s’adonner à des occupations qui demandent moins de scolarité parce qu’ils sont dotés d’une aversion pour les études.
En d’autres termes, l’abandon scolaire rationnel et basé sur l’existence d’avantages comparatifs n’est pas incompatible avec la corrélation entre éducation des parents et des enfants. Cependant, la situation concernant les jeunes garçons est plus étrange.
Premièrement, un tel différentiel entre garçon et fille est tout à fait nouveau, en dépit du fait qu’un grand certain nombre d’études ont dejà noté que les jeunes filles tendent à obtenir de meilleures notes que les jeunes garçons. Deuxièmement, comme les goûts et habiletés devraient normalement être distribués également entre les garçons et les filles, un différentiel significatif entre les garçons et les filles est tout à fait inattendu. Ceci explique que le taux d’abandon scolaire est anormalement élevé au Québec.
Parties annexes
Remerciements
Je remercie le ministère des Finances du Québec pour l’aide financière apportée à ce projet, Nathalie Viennot-Briot pour le travail accompli sur les données et Claude Montmarquette pour ses commentaires.
Notes
-
[1]
Ce problème est analysé dans une publication du ministère canadien des Ressources humaines intitulé « À la croisée des chemins » datant de 2001.
-
[2]
Voir Dagenais, Montmarquette et Viennot-Briot (2001).
-
[3]
Pour plus de détails, le lecteur peut consulter Parent (2002).
-
[4]
L’incidence du retour à l’école après l’âge de 24 ans est pratiquement négligeable.
-
[5]
Le National Longitudinal Survey of Youths est l’échantillon de jeunes Américains utilisé par tous les auteurs précédemment cités.
-
[6]
Pour plus de details, voir Cameron et Heckman (2001), Magnac et Thesmar (2001) ou Chen, Heckman and Vitlacyl (1999).
-
[7]
Les répondants ont aussi eu la possibilité de choisir un niveau d’éducation autre que celui représenté par les choix mentionnés précédemment; un Ontarien l’a fait, mais aucun Québécois.
-
[8]
Voir Belzil et Hansen (2002, 2003) et Cameron et Heckman (1998).
Bibliographie
- Belzil, Christian et Jörgen Hansen (2002), « Unobserved Ability and the Return to Schooling », Econometrica, 70 : 575-591.
- Belzil, Christian et Jörgen Hansen (2003), « Structural Estimates of the Intergenerational Education Correlation », Journal of Applied Econometrics, 18(6) : 679-696.
- Cameron, Stephen et James Heckman (1998), « Life Cycle Schooling and Dynamic Selection Bias: Models and Evidence for Five Cohorts of American Males », Journal of Political Economy, 106 (2) : 262-333.
- Cameron, Stephen et James Heckman (2001), « The Dynamics of Educational Attainments for Black, Hispanic, and White Males », Journal of Political Economy, 109(3) : 455-499.
-
Chen, Xiaohong, James Heckman et Edward Vytlacyl (1999), « Identification and
 Efficient Estimation of Semiparametric Panel Data Models with Binary Dependent Variables and a Latent Factor », Cahier de recherche.
Efficient Estimation of Semiparametric Panel Data Models with Binary Dependent Variables and a Latent Factor », Cahier de recherche.
- Dagenais, Marcel, Claude Montmarquette et Nathalie Viennot-Briot (2001), « Drop out, School Performance and Working While in School: An Econometric Model with Heterogeneous Groups » Cahier de recherche, CIRANO, Montréal.
- Eckstein, Zvi et Kenneth Wolpin (1999), « Youth Employment and Academic Performance in High School », Econometrica, 67 : 575-596.
- Kane, Thomas (1994), « College Entry by Blacks since 1970: The Role of College Costs, Family Background, and the Returns to Education » Journal of Political Economy, 102 : 878-911.
- Keane, Michael P. et Kenneth Wolpin (1997), « The Career Decisions of Young Men », Journal of Political Economy, 105(3) : 473-522.
- Parent, Daniel (2002), « La prime associée au diplôme d’études secondaires et le décrochage scolaire au Canada », Rapport de projet, CIRANO.
- Rosenzweig, Mark et Kenneth Wolpin (2000), « Natural Experiments in Economics », Journal of Economic Literature, Décembre : 827-874.
- Sauer, Robert (2004), « Education Financing and Lifetime Earnings », Review of Economic Studies, 71(4).
Liste des tableaux
Tableau 1
Quelques statistiques descriptives
A
Niveaux de scolarité au Québec et en Ontario en 1995
B
Niveau de scolarité des parents au Québec et en Ontario
Tableau 3
Paramètres estimés par maximum de vraisemblance
Tableau 4
Modèle avec interaction entre sexe et composition familiale – paramètres estimés par maximum de vraisemblance
Tableau 5
Importance relative des variables explicatives
Tableau 6
Changements dans les taux moyens de décrochage scolaire sous divers scénarios
Tableau 7
Rendements en éducation (revenus hebdomadaires)