Corps de l’article

Introduction

Depuis le début des années soixante-dix, le nombre de crises financières frappant les pays émergents, mais aussi les pays industrialisés a fortement augmenté. Les crises financières récentes, qui selon Eichengreen et Bordo (2003) ainsi que Bordo (2006) sont nettement plus sévères, désorganisatrices et coûteuses que les crises financières observées durant le régime de l’étalon-or, conduisent à des ajustements importants des balances des paiements, des taux de change et des rythmes de croissance. Cette littérature récente rend bien compte des effets dévastateurs des crises financières de la fin du xxe siècle et discrimine clairement entre le renversement du solde courant qui concerne essentiellement les pays industrialisés et l’arrêt brutal qui s’applique essentiellement aux pays à marchés émergents. Cependant, la majorité de ces travaux porte sur le niveau des variables, notamment le taux de change, alors que la vitesse à laquelle une monnaie nationale s’est modifiée face à la devise étrangère peut s’avérer particulièrement dommageable pour les entrepreneurs nationaux puisque les seuils de compétitivité internationale des différents secteurs productifs de l’économie sont modifiés.

Dans cette étude, l’approche considérée diffère fondamentalement des interprétations en termes de renversement du solde courant ou d’arrêt brutal des afflux de capitaux. Elle peut participer à une meilleure compréhension des mécanismes liant les comptes extérieurs au taux de change, puisque l’accent est mis sur la vitesse d’évolution, c’est-à-dire sur les taux de croissance des taux de change réel. Il s’agit d’une méthodologie peu usitée dans la littérature sur les taux de change.

Le point de départ et le soubassement théorique de cette analyse sont constitués par la classe des modèles de croissance économique contrainte par l’équilibre de la balance des paiements. Le modèle initiateur de cette analyse a été développé en 1979 par Thirlwall puis en 1982 (Thirlwall et Hussain, 1982). Leur cadre postkaldorien permet de conclure que le rythme de croissance du taux de change réel compatible avec un équilibre extérieur dépend d’une part des rythmes de croissance du revenu réel domestique et étranger, d’autre part des élasticités du commerce extérieur.

Ce modèle initial est amendé afin d’accroître sa pertinence eu égard à l’intégration des marchés financiers internationaux et à l’importance des flux internationaux de capitaux dans le financement des déséquilibres extérieurs d’une économie. Il inclut un premier bloc qui décrit la contrainte extérieure qui s’impose sans exception à toute nation. À long terme, une nation ne peut s’endetter quelle que soit sa taille. Cela permet de définir les rythmes de croissance du produit national et du taux de change réel compatibles avec cet équilibre extérieur. Un second bloc est construit qui reprend la contrainte extérieure étendue aux mouvements de capitaux. À moyen terme, l’économie peut subir un déséquilibre courant temporaire s’il est intégralement compensé par des flux nets de capitaux. Autrement dit, on suppose qu’une balance de base doit être équilibrée. Il est alors possible de déterminer les rythmes de croissance du produit national et du taux de change réel compatibles cette fois avec cette contrainte extérieure étendue aux flux internationaux de capitaux.

L’objectif est alors de montrer que la relation entre le taux de croissance du taux de change réel et les rythmes de croissance du revenu réel entre les pays et les flux nets de capitaux de long terme dépend de cette double contrainte sur les comptes extérieurs que subissent les nations. C’est l’articulation de ces deux blocs qui va définir le rythme d’appréciation ou de dépréciation du taux de change réel d’équilibre, c’est-à-dire le taux de croissance du taux de change réel.

La prochaine section fait un rappel de la littérature récente sur les ajustements des comptes extérieurs. Elle présente et explicite ensuite le modèle de Thirlwall (1979). La section qui suit détaille alors les innovations apportées à ce premier modèle. Dans la troisième section, il est alors possible d’observer que le rythme de croissance du taux de change réel est étroitement conditionné par les évolutions comparées des revenus réels domestique et étranger puis des effets conjoints des élasticités du commerce extérieur, puis que les réactions à un choc exogène, comme un arrêt brutal des afflux de capitaux, dépendent étroitement des caractéristiques de la combinaison des élasticités du commerce extérieur. La dernière section conclut.

1. Revue de la littérature

Les dernières décennies montrent l’importance des déficits courants et le rôle que peut jouer l’arrêt brutal des flux de capitaux dans l’apparition des crises financières. Différentes approches ont participé à ces analyses. Mais elles conduisent fréquemment à des interprétations théoriques parfois peu compatibles entre elles, voire à des résultats empiriques ambigus d’autant qu’elles sont essentiellement en termes de flux (Knight et Scacciavillani, 1998; Miller, 2002; Edwards 2002). Elles ne considèrent pas que les vitesses d’ajustement des variables macroéconomiques puissent avoir des effets tout autant dommageables sur une économie en raison des rythmes d’ajustements plus lents sur les marchés réels que sur le marché des changes et des capitaux. L’approche développée par Thirwall (1979) peut ainsi être particulièrement pertinente car elle met l’accent sur ces taux de croissance, tout en contribuant à une meilleure compréhension des liens entre équilibre extérieur, taux de change réel et croissance économique. Elle tranche ainsi avec les cadres précédents.

1.1 Retournement des comptes courants ou arrêt brutal des afflux de capitaux

L’approche intertemporelle du solde courant, qui constitue l’une des pièces maîtresses de la nouvelle macroéconomie internationale s’inspire directement des estimations empiriques de Sachs (1981) et des innovations théoriques de Obstfeld et Rogoff (1994, 1996). Elle se concentre sur les causes domestiques du déséquilibre courant par l’intermédiaire de l’analyse de l’épargne et de l’investissement. Dans ce contexte de parfaite intégration des marchés des capitaux et de taux d’intérêt fixes, les agents économiques d’un petit pays, où les prix sont fixes, ont un comportement d’optimisation intertemporelle. La capacité de prêt ou d’emprunt d’une économie dépend alors du lissage intertemporel de la consommation. Le solde courant est un phénomène qui se déduit des décisions de long terme des agents économiques en matière d’investissement et d’épargne. Un déficit persistant d’un solde courant n’est pas préoccupant lorsqu’il résulte des comportements optimisateurs des agents économiques qui adapteront leur plan de consommation en fonction de nouvelles informations et afin de générer les ressources nécessaires à l’équilibre intertemporel.

Ignorant le compte financier de la balance des paiements, ce cadre d’analyse considère le taux de change comme la variable d’ajustement dont la modification sera d’autant plus importante que les marchés réels seront segmentés et que les économies seront relativement fermées. Mais, la difficulté à obtenir des résultats de long terme qui soient réalistes[1] suggère de se concentrer sur d’autres catégories de travaux dont la diversité des méthodologies empiriques mises en oeuvre témoigne implicitement de la difficulté à l’homogénéisation théorique. Les analyses sont nombreuses et deux interprétations sur les six catégories que détaillent Kaminsky (2006) apparaissent omniprésentes. La première considère qu’un pays qui a atteint un certain niveau de déficit courant est susceptible de subir sur une période limitée un retournement du solde courant. La seconde se concentre sur l’arrêt brutal des afflux de capitaux qui déséquilibre la balance des paiements. Bien qu’Edwards (2004a) rappelle que ces deux notions demeurent statistiquement liées, elles apparaissent distinctes puisque la première se concentre sur le haut, alors que la seconde porte sur le bas de la balance des paiements.

Dans leur article remarqué sur les retournements des soldes courants, Milesi-Ferretti et Razin (1998) montrent qu’une économie qui a atteint un déficit courant important est susceptible de subir un retournement significatif du solde courant sur une période limitée. Ce dernier, dont Eichengreen et Adelet (2005) précisent que la fréquence est plus importante depuis 1972 que pendant les régimes monétaires antérieurs, se produit essentiellement au sein de pays dont le déficit courant s’approche d’un seuil. Freund (2005), mais aussi Mann (2002), établissent une fourchette de 4 à 5 % du PIB[2]. Lorsqu’elle est atteinte, un ajustement se produit, qui peut durer de 3 à 4 ans. Il combine une dépréciation du taux de change réel de 10 à 20 % avec un ralentissement de la croissance domestique. Lorsque le renversement du solde courant est brusque et rapide, le déclin de l’investissement domestique et du revenu par tête peut être plus important (Edwards, 2006). Cependant, Freund et Warnock (2005) précisent que cela peut aussi s’associer à une augmentation du déficit budgétaire et à une relance de la croissance des exportations réelles. Toutefois, Edwards (2004b, 2005) montre que les effets sont d’autant plus accentués sur la croissance qu’il s’agit de petites économies émergentes, qu’elles sont relativement fermées au commerce international ou que le régime de changes est favorable aux parités fixes puisqu’il sera plus difficile d’ajuster les prix relatifs. Ces preuves empiriques peuvent apparaître fragiles puisque Debelle et Galati (2005) échouent à relier les effets des ajustements du solde courant sur le revenu domestique et sur le taux de change au sein de pays industrialisés.

Une réduction de la croissance domestique, voire une récession économique associée à une large dépréciation des taux de change, peuvent aussi se produire sans que le renversement du compte courant soit l’événement générateur (Hutchison et Noy, 2006). Les principales causes peuvent être une agitation financière, une augmentation des taux d’intérêt mondiaux, ou une modification de l’appréhension par les marchés de la soutenabilité de la dette extérieure. La principale conséquence est alors l’arrêt brutal des afflux de capitaux dont la notion, théorisée par Calvo (1998) et Calvo et Reinhart (2000), correspond à « une réduction abrupte et significative des afflux de capitaux vers un pays qui jusqu’à présent recevait de larges volumes de capitaux nets étrangers » (Calvo, 2003 : 1; Edwards, 2007 : 2) et peut aussi s’associer à un élargissement du spread de taux entre les économies émergentes (Calvo, Izquierdo et Talvi, 2006). La demande de biens se réduit à la suite d’un arrêt brutal des afflux de capitaux et le taux de change réel se déprécie afin de restaurer l’équilibre sur le marché des biens. Frankel et Cavallo (2004), Calvo, Izquierdo et Meija (2004) mais aussi Calvo, Izquierdo et Talvi (2003) montrent que l’ajustement du change sera alors d’autant plus important que l’économie est relativement fermée. Ces derniers nuancent toutefois les conclusions car ils rappellent qu’à l’inverse du renversement du solde courant, les autorités monétaires peuvent mobiliser les réserves de changes lorsqu’elles sont en quantités suffisantes afin d’éviter l’ajustement brutal et ultérieur des comptes extérieurs.

Ces approches sont en termes de flux. Elles occultent les vitesses d’ajustement des variables du taux de change ou de la croissance économique. Or, ces vitesses peuvent être tout autant dommageables pour une économie[3]. Si les variations des taux de change réels sont néfastes pour une économie en raison des effets destructurants sur la compétitivité domestique, il est aussi important de souligner que l’accélération de la vitesse d’évolution du taux de change réel peut avoir des effets aussi dévastateurs. La rapidité avec laquelle les mouvements du change réel se réalisent modifie les comportements d’investissement des entreprises et ne leur permet pas de renégocier l’ensemble de leurs contrats, ni d’opérer dans des délais raisonnables les ajustements nécessaires pour incorporer dans leur structure de coûts les effets induits par les modifications du change. Les structures productives ne disposent plus d’un délai suffisant pour s’adapter aux évolutions du cours du change, alors que les agents économiques ne sont plus en mesure de conclure que la dynamique du taux de change réel est un phénomène transitoire ou permanent.

Un modèle théorique postkaldorien développé par Thirlwall (1979) et Thirlwall et Hussain (1982) de croissance contrainte par la balance des paiements autorise une analyse où l’accent est mis sur les vitesses d’ajustements des variables. Ce modèle relie les rythmes de croissance du taux de change réel et du revenu domestique réel sous contrainte d’équilibre des comptes extérieurs.

1.2 Un modèle postkaldorien de croissance contrainte par l’équilibre extérieur

Ce modèle n’a ni fondement microéconomique, ni référence aux ajustements internes. L’économie est de petite taille et totalement ouverte. Il n’y a donc pas de secteur protégé. L’accent est mis sur la demande. L’offre est exogène car les valeurs des élasticités de l’offre sont supposées infinies. Seul le secteur réel est pris en considération. Il n’y a pas d’éléments financiers. Les prix domestique et étranger peuvent varier sous la condition que le différentiel d’inflation entre la nation et l’étranger demeure inchangé. Le taux de change nominal est parfaitement flexible. Le modèle comprend quatre équations[4] :

Les lettres f, x, m, y et z sont respectivement les flux nets de capitaux de long terme, les volumes des exportations, des importations, du revenu de l’économie domestique et étrangère. Ce dernier est considéré en un seul bloc. L’indice t présente la date et les lettres e, p et pe décrivent respectivement le taux de change nominal à l’incertain, les prix domestiques et étrangers. La relation (1) présente l’expression dynamique de la balance des paiements. L’équation (2) définit la part des exportations dans le total des flux de capitaux de la nation. Le ratio θ est constant. Le modèle est bouclé avec les équations (3) et (4). Elles présentent respectivement la demande d’exportations et d’importations des biens manufacturés. Les paramètres α0, β0 ainsi que α1 et β1 désignent respectivement les élasticités-revenu des exportations et des importations ainsi que les élasticités-prix des exportations et des importations. Ils sont tous strictement positifs. Ces paramètres constituent des indicateurs appréciables mais non exclusifs de la spécialisation internationale[5].

La résolution de ce système d’équations permet de déduire le taux de croissance du revenu domestique réel qui est compatible avec l’équilibre dynamique des comptes extérieurs. Après avoir posé que le taux de croissance du taux de change réel est : ṡt = ėt + ṗte – ṗt , il est alors possible d’écrire :

Ce rythme de croissance qui est compatible avec l’équilibre extérieur ẏt est une fonction linéaire du taux de croissance du revenu étranger żt, du taux de croissance du taux de change réel ṡt et des flux nets de capitaux réels (ḟt –ṗt). Leurs effets seront plus ou moins importants selon les valeurs des élasticités-prix (α1 et β1), des élasticités-revenu (α0 et β0) et de θ.

Lors des discussions[6], les auteurs supposent que la concurrence par les prix annule à long terme les gains ou pertes de compétitivité-prix et qu’un pays ne peut accepter à long terme un déséquilibre persistant de ses comptes extérieurs. Il est posé que ṡt = 0 et θ = 1. L’équation (5) devient ẏt = (α0 / β0) żt. Ils nomment cette relation « la loi fondamentale ». En moyenne, le rythme de croissance domestique compatible avec l’équilibre commercial ne peut excéder le produit du rapport des élasticités-revenu (α0 / β0) avec le rythme de croissance du revenu réel étranger żt sous peine de subir un déséquilibre courant. Cette loi a fait l’objet de nombreuses vérifications empiriques qui confirment sa validité. De nombreuses études appliquées à des pays ayant des caractéristiques différentes (León-Ledesma, 1999 pour l’Espagne, Bairam et Dempster, 1991 pour les pays producteurs de pétrole et en développement puis Bairam, 1988; Andersen, 1993; Perraton et Turner, 1999 ainsi que Christipoulos et Tsionas, 2003 pour les pays industrialisés) montrent que le rythme de croissance du revenu domestique réel observé diffère peu de celui que prédit la loi fondamentale. Autrement dit, les pays dont la valeur de (α0 / β0) est nettement supérieure à l’unité sont aussi ceux qui bénéficient en moyenne d’un rythme de croissance du revenu domestique réel plus élevé que celui des principaux partenaires commerciaux. Les nations qui adoptent des rythmes de croissance domestique réels inférieurs à ce que prédit la loi fondamentale dégagent des excédents commerciaux, comme ce fut le cas pour le Japon et la RFA durant les années quatre-vingt. Ceux dont le rythme de croissance excède celui que prédit la loi fondamentale subissent un déficit courant, comme les États-Unis (Atesoglu, 1993; McCombie, 1997).

La validité de la loi fondamentale dépend de l’acceptation ou non de l’hypothèse sur les taux de change réel et implicitement de la validité de la parité des pouvoirs d’achat (PPA). Or, il y a une incompatibilité forte entre l’hypothèse de stationnarité du taux de change réel et les résultats des tests économétriques récents sur la PPA. Le cadre temporel retenu par les études, qui tentent de valider la loi fondamentale, porte sur des estimations des fonctions du commerce extérieur sur des périodes de 10 à 15 ans. À une telle échéance, il est acceptable de supposer que les élasticités ne varient pas. Or sur une décennie, voire deux, les tests qui sont conduits sur la PPA et portant sur des périodes sensiblement identiques indiquent clairement que la stationnarité des taux de change réels n’est nullement acquise tant pour les pays industrialisés que pour les pays en voie de développement[7]. La validité de la PPA se retrouve majoritairement sur des longues séries temporelles qui concernent au moins le siècle. Or, il est nécessaire d’être prudent sur d’aussi longues périodes à cause de la fragilité des données alors que l’estimation des fonctions du commerce extérieur sur des périodes semblables impliquerait vraisemblablement des élasticités du commerce extérieur variables, alors qu’il est implicitement stipulé qu’elles demeurent inchangées.

La construction de θ conduit à ne s’intéresser qu’aux nations qui sont structurellement importatrices nettes de capitaux. Par construction les nations créancières nettes sont exclues, d’autant qu’introduire une variable reflétant les flux nets de capitaux et considérer qu’à long terme ces mouvements de capitaux n’exercent aucune influence sur l’équilibre extérieur équivaut malgré tout à supposer l’absence de flux internationaux de capitaux (c’est-à-dire θ = 1). Une considération plus adaptée des flux de capitaux suppose de prendre en compte aussi bien les nations créancières nettes que celles qui sont débitrices nettes.

Si le modèle s’inscrit dans le court ou moyen terme, la validité selon laquelle ṡt = 0 et θ = 1 devient incertaine. Le taux de change réel ne peut plus être fixe et la balance courante n’a plus de raisons d’être systématiquement à l’équilibre. Dès lors, il est possible de poser que ṡt ≠ 0 et que θ ≠ 1.

2. Les rythmes de croissance du taux de change réel compatible avec un équilibre extérieur

Deux innovations sont apportées dans ce modèle. Il s’agit toujours d’une économie de petite taille totalement ouverte sur l’extérieur, mais l’hypothèse selon laquelle la parité des pouvoirs d’achat est valide, conduisant à considérer que le rythme de croissance du taux de change réel est nul à long terme, est remise en question. Le taux de croissance du taux de change réel est alors relié aux différentes variables de politique économique, comme le taux de croissance du revenu réel. La seconde innovation réside dans la description de l’équilibre extérieur. Cela conduit à préciser deux expressions du taux de croissance du taux de change réel selon l’équilibre extérieur considéré. La première suppose que le rythme de croissance du taux de change réel est compatible avec un taux de couverture donné. La seconde permet de déduire le rythme de croissance du taux de change réel compatible avec un solde courant compensé par des flux nets de capitaux. La forme réduite constitue le modèle BB-BC.

2.1 Taux de change réel et les équilibres extérieurs

Le modèle amendé comprend quatre relations. Les deux premières reprennent les précédentes équations (3) et (4). Les deux autres relations décrivent le comportement dynamique de l’équilibre extérieur. En rappelant que le taux de croissance du taux de change réel est : ṡt = ėt + ṗte – ṗt , le modèle s’écrit :

L’équation (6) décrit la condition d’équilibre permanent du compte courant. L’équilibre extérieur s’exprime à partir du solde de la balance de base à la date t, BBt. C’est la somme algébrique du solde commercial, Xt – StMt et du solde des mouvements de capitaux, PtFt. Par définition, on appelle Ft le volume du solde des capitaux de long terme nets des revenus des capitaux[8]. Ce dernier est considéré comme exogène. Pour simplifier, notamment parce qu’ils sont fréquemment d’une faible valeur, les transferts et les revenus des facteurs sont aussi exclus[9]. Le volume du solde extérieur s’écrit alors : BBt = Xt – StMt+ Ft. Lorsque : Xt – StMt+ Ft = 0, les comptes extérieurs sont équilibrés à toute date. La différentielle s’écrit alors : dXt – MtdSt – StdMt + dFt = 0. Si l’actif net Ft n’est pas nul, on déduit que Xtẋt – StMt (ṡt + ṁt ) + Ftḟt = 0. Par définition, le taux de couverture d’une économie à la date t est le rapport des exportations et des importations exprimées dans la même unité monétaire, τt = Xt / StMt. La relation (6) se déduit aisément.

L’équation (7) pose l’hypothèse selon laquelle le taux de couverture est constant à moyen terme (τ̇t = 0). Lorsque le taux de couverture est constant (τ̇t = 0), alors le taux de croissance des exportations est systématiquement égal à la somme des taux de croissance du taux de change réel et des importations en volume. Cette hypothèse systématiquement supposée selon laquelle τt est constant et exogène à moyen terme (τt = τ) a certes un caractère simplificateur. Cependant, elle se justifie doublement. Elle permet d’abord de rendre linéaire la dynamique du modèle. Si τt variait à chaque période, la dynamique qui serait dégagée serait complexe, sans qu’il soit raisonnable de considérer que cela soit apte à dégager des règles d’interprétation pertinentes pour un taux de change d’équilibre de moyen terme alors même que la contrainte extérieure demeure inchangée. De plus, le cadre temporel retenu étant de moyen terme et non de long terme, les élasticités du commerce extérieur sont constantes puisque les processus générateurs des séries des exportations et des importations demeurent inchangés. Un pays durablement importateur ou exportateur net de capitaux ne peut pas s’attendre à observer une modification substantielle de son statut financier sur la période.

2.2 Le modèle BB-BC

Ce modèle comprend deux blocs et sa forme structurelle est donnée par les relations (3), (4), (6) et (7). Le premier bloc se réfère à l’équilibre de la balance courante. Le second bloc définit l’équilibre d’une balance courante compensée par des flux de capitaux de long terme.

La combinaison des équations (3), (4) et (7) décrit le premier bloc (BC). Il fournit l’expression du taux de croissance du taux de change réel ṡtBC compatible avec l’équilibre extérieur :

Ce taux de croissance du taux de change réel compatible avec un taux de couverture constant résulte de l’effet combiné d’une part de facteurs conjoncturels comme les rythmes de croissance des revenus réels de l’économie domestique et étrangère et d’autre part des facteurs structurels comme les élasticités du commerce extérieur.

Le premier ensemble d’effets réside dans la comparaison des rythmes de croissance des revenus réels domestique et étranger pondérés par les élasticités-revenu du commerce extérieur [β0ẏt– α0żt]. Si les taux de croissance du revenu domestique et étranger sont strictement semblables (ẏt = żt), alors le rythme de croissance du taux de change réel sera conditionné par l’écart entre l’élasticité-revenu des exportations et celle des importations. Lorsque la configuration d’élasticités-revenu est favorable (c’est-à-dire α0 / β0 > 1), le rythme de croissance du taux de change réel aura tendance à se réduire (c’est-à-dire ṡtBC < 0), puisque cela résulte d’une combinaison favorable des conjonctures économiques et des élasticités-revenu du commerce extérieur (c’est-à-dire [β0ẏt– α0żt] < 0). Dans le cas inverse, l’association accélération du rythme de croissance du revenu domestique réel et dépréciation accélérée du taux de change réel peut être sans limite en l’absence de tensions internes, notamment en termes de contraintes sur l’offre de facteurs à même de favoriser la croissance réelle plus intense au sein de l’économie. Tant que l’on admet qu’il n’y a pas de contraintes internes sur l’offre, il peut s’agir d’une configuration favorable à l’économie domestique[10]. Mais, si les élasticités-revenu sont proches (c’est-à-dire α0 / β0 ≅ 1), alors le taux de change réel de l’économie domestique ne devrait pas se déprécier sauf si le rythme de croissance du revenu réel de l’économie domestique excède celui du reste du monde.

L’effet de ce premier ensemble de facteurs structurels et conjoncturels sera accentué ou affaibli selon la pente de la droite reliant le rythme de croissance du change réel avec le rythme de croissance du revenu domestique réel (c’est-à-dire (1 / (α1 + β1 – 1))). Le numérateur (α1 + β1 – 1) qui correspond au critère de Marshall-Lerner exerce une influence cruciale. Toutes choses égales par ailleurs, plus la somme des élasticités-prix du commerce extérieur (c’est-à-dire α1 + β1) excède strictement l’unité, plus la pente sera faible et moins le taux de change réel sera sensible à une variation donnée du rythme de croissance du revenu domestique réel. À l’inverse, de faibles valeurs des élasticités-prix mènent à une variation relativement plus significative du taux de change réel, à la suite d’une variation identique du rythme de croissance du revenu domestique réel, en raison d’une pente de la droite (BC) plus forte.

La combinaison des équations (4), (5) et (6) compose le bloc (BB) et permet de déduire une expression du rythme de croissance du taux de change réel compatible avec l’équilibre courant compensée par des flux nets de capitaux ṡtBB [11]. Ce dernier s’écrit :

Ce taux de change réel compatible avec l’équilibre courant compensé par des flux nets de capitaux dépend de l’effet combiné des élasticités du commerce extérieur et des variables de politiques économiques. La comparaison de (BB) avec (BC) montre deux différences importantes. La première provient de la présence du taux de couverture τ qui affecte à la fois le différentiel de croissance entre les pays et la pente de la relation (BB) sur un plan (ẏt , ṡt). La seconde résulte de l’existence des flux nets de capitaux de long terme qui conditionnent l’ordonnée à l’origine de la droite (BB). Dès lors, ce taux de croissance du taux de change réel compatible avec l’équilibre courant compensée par des flux nets de capitaux dépend de trois effets majeurs.

Le premier est décrit par le jeu combiné des écarts de croissance entre économies, pondéré par les élasticités-revenu du commerce extérieur [β0ẏt– τα0żt]. La principale différence, en comparaison de l’équation (BC), réside dans le taux de couverture τ qui accentuera ou au contraire réduira l’impact d’une variation donnée de żt sur le terme ṡtBB. Si la configuration d’élasticités-revenu est favorable (c’est-à-dire α1 / β1 > 1), le rythme de croissance du taux de change réel aura tendance à se réduire d’autant plus vite (c’est-à-dire ṡtBB < 0), que le taux de couverture excède strictement l’unité puisqu’il aura pour effet d’augmenter l’impact de l’élasticité-revenu des exportations sur le rythme de croissance du revenu du reste du monde żt. À l’inverse, une valeur faible du taux de couverture (c’est-à-dire τ < 1) réduira l’impact du rythme de croissance du reste du monde sur l’évolution du taux de change réel, même si la configuration d’élasticités-revenu est favorable.

Le second effet réside dans la pente de la droite reliant le rythme de croissance du change réel compatible avec l’équilibre extérieur et le rythme de croissance du revenu domestique réel, qui devient 1 / (τα1 + β1 – 1) au lieu de 1 / (α1 + β1 – 1). La différence entre les deux pentes dépend alors uniquement du taux de couverture τ. Le numérateur τα1 + β1 – 1 décrit la condition de Marshall-Lerner amendée puisque le taux de couverture est pris en compte. Plus le taux de couverture sera élevé, plus la pente de (BB) sera faible et moins importante sera la modification du rythme de croissance du taux de change réel à la suite d’une variation donnée du rythme de croissance du revenu domestique réel. Le terme τα1 + β1 – 1 peut devenir négatif, malgré une valeur strictement positive de (α1 + β1 – 1), si le taux de couverture est suffisamment réduit, (c’est-à-dire τ < (1 – β1) / α1). Il en résulte une diminution du rythme de croissance du taux de change réel alors que le rythme de croissance du revenu domestique réel augmente.

Enfin, la dernière série d’effets, qui constitue aussi une différence majeure avec l’expression décrite par (BC) réside dans l’effet financier sur le taux de croissance du taux de change réel. Cet effet s’exprime par – [(1 – τ) / (τα1 + β1 – 1)] ḟt. À nouveau, le taux de couverture exerce une influence significative, puisque trois cas peuvent être mis en avant lorsque l’économie bénéficie d’une croissance des créances sur l’étranger (ḟt > 0). D’abord, un excédent extérieur structurel, qui se caractérise par τ > 1 mène à une dépréciation plus importante ou une appréciation plus faible du taux de change réel. Ensuite, l’association d’un solde commercial structurellement déficitaire (τ < 1) mais qui demeure suffisamment élevé (c’est-à-dire τ > (1 – β1) / α0) pour que le critère de Marshall-Lerner amendé demeure vérifié (τα1 – β1 – 1 > 0), induit une dépréciation à un rythme plus faible ou à une appréciation à un rythme plus élevé du taux de change réel. Enfin le rythme de dépréciation du taux de change réel aura tendance à s’accélérer si le critère de Marshall-Lerner amendé n’est plus valide (τα1 – β1 – 1 < 0), parce que τ < (1 – β1) / α0 est observé. L’effet sur le taux de change réel est inversé.

2.3 L’équilibre

Dans l’hypothèse où les variables exogènes sont toutes supposées constantes (ḟt = ḟ, żt = ż), la forme structurelle en (ẏt, ṡt) est donnée par le système qui suit. On admet évidemment que α1 + β1 – 1 ≠ 0 et τα1 + β1 – 1 ≠ 0. Pour en simplifier l’écriture, il est posé que :

equation: 038709are012n.png

equation: 038709are013n.png

L’intersection des deux droites (BB) et (BC) détermine les valeurs d’équilibre du taux de croissance du revenu domestique réel et du taux de croissance du taux de change réel compatible avec les rythmes de croissance d’équilibre de la balance courante et de la balance de base. Une fois cet équilibre atteint, les taux de croissance du taux de change réel et de la croissance domestique sont constants. Les coordonnées du point d’équilibre sont :

equation: 038709are014n.png

Dans un plan orthonormal (0ẏt, 0ṡt) il est possible de présenter les droites représentatives de (BB) et (BC) où les valeurs des variables exogènes : żt = ż et ḟt = ḟ sont supposées constantes. L’axe des abscisses indique le taux de variation du rythme de croissance du revenu domestique réel. L’axe des ordonnées définit le taux de variation du taux de change réel. Le long de (BC), les modifications du couple (ẏt, ṡt) se réalisent à taux de couverture constant. Mais le taux de couverture est croissant (décroissant) lorsque l’économie se situe à gauche (droite) de (BC). Ensuite, pour qu’une accélération du rythme de croissance réelle domestique, qui majore les importations, puisse néanmoins assurer le retour à l’équilibre de la balance courante, il est nécessaire que le rythme de croissance du taux de change réel s’accélère. Cela revient à poser que le critère de Marshall-Lerner est toujours vérifié (α1 + β1 – 1 > 0), ce qui est conforme avec de nombreux travaux théoriques qui imposent d’emblée cette hypothèse. Cela assure la stabilité du modèle et restreint le nombre de cas afin de mettre l’accent sur les cas qui sont économiquement pertinents. Les multiples estimations contemporaines des fonctions d’exportations et d’importations qui suggèrent qu’en règle générale les élasticité-prix sont suffisamment élevées pour que leur somme excède strictement l’unité confirment aussi cette hypothèse (Hooper et al., 1998; Marquez, 2002). La pente de (BC) s’impose aux nations car les élasticités du commerce extérieur sont constantes, mais elle peut être différente selon les pays car la pente dépend de l’effet combiné des élasticités du commerce extérieur.

La droite (BB) décrit l’équilibre de la balance de base. Le long de la droite (BB), le taux de croissance du solde courant et les flux nets de capitaux se compensent parfaitement. Il y a une infinité de couples (ẏ, ṡ) compatibles avec un rythme de croissance d’équilibre de la balance de base, c’est-à-dire un solde courant qui est parfaitement compensé par des flux nets de capitaux. La superposition des droites (BB) et (BC) correspond au cas unique où τ = 1, puisque la pente de (BB) dépend de la valeur du taux de couverture τ. Lorsque τ diffère de l’unité, les pentes des droites (BB) et (BC) sont différentes. Par conséquent, si τ est supérieur (respectivement : inférieur) à l’unité, alors la pente de la droite (BB), devient inférieure (respectivement : supérieure) à la pente de la droite (BC). La balance de base croit alors à un taux respectivement positif (négatif) à gauche (droite) de (BC).

L’incidence du taux de couverture sur la pente de (BB) puis sur la position de (BB) relativement à celle de (BC) doit être prise en considération lorsque l’on souhaite évaluer la capacité de réaction d’une économie totalement ouverte sur l’extérieur à un choc exogène, comme des variations nettes des flux de capitaux. Pour un rythme de croissance domestique donné, l’écart entre (BC) et (BB) permet soit d’identifier les éventuels mouvements nets de capitaux dont l’économie a besoin pour solder les comptes extérieurs, soit de quantifier les modifications brutales du taux de croissance du taux de change réel théoriquement nécessaires pour restaurer le rythme de croissance d’équilibre du solde courant, puisque l’écart de pente entre ces deux droites dépend en définitive de la valeur du taux de couverture.

3. Les évolutions des taux de change réel d’équilibre extérieur

Lorsqu’une économie de petite taille et totalement ouverte subit un choc exogène comme une diminution soudaine et autonome des créances nettes sur l’étranger, le rythme de croissance d’équilibre du taux de change réel de moyen terme et le rythme de croissance du revenu domestique réel seront modifiés puisque la balance courante compensée par des flux nets de capitaux de long terme est affectée alors que la droite compatible avec l’équilibre courant demeure inchangée. Les causes d’un tel choc sur le bas de la balance des paiements peuvent être nombreuses comme une augmentation de l’ouverture de ses marchés des capitaux en libéralisant le compte de capital ou une modification de la confiance des marchés à la suite d’informations exogènes (risque-pays modifié à la suite d’un endettement croissant ou d’une crise financière ou bancaire, changement inattendu de la politique économique pour faire face à des difficultés conjoncturelles, crédibilité moindre des actions publiques, concurrence internationale aiguisée par la montée en puissance de certains pays qui mène une modification des flux d’investissements étrangers…).

Le passage de l’équilibre initial E0 à l’équilibre final E1 et la position de ce dernier dans le plan (0ẏ, 0ṡ) sont conditionnés d’une part par l’ampleur du choc exogène, d’autre part par les pentes relatives de (BC) et de (BB), enfin par le taux de couverture. La position relative des deux courbes dans le plan (0ẏ, 0ṡ) a un impact sur la nature stable ou instable du point d’équilibre stationnaire puisque la situation économique n’est pas la même suivant que la pente de la droite (BB) est plus ou moins forte relativement à celle de (BC). À l’exception du cas particulier où le taux de couverture correspond à l’unité, signe d’un équilibre permanent de la balance courante, la valeur du taux de couverture affecte nécessairement le terme τα1 + β1 – 1. Le critère de Marshall-Lerner amendé sera ou ne sera pas vérifié selon les valeurs du taux de couverture τ et la stabilité du modèle dépend fortement du signe de τα1 + β1 – 1. Dès lors, la description de la dynamique d’ajustement des comptes extérieurs est conditionnée par la distinction qui doit être effectuée entre α1 + β1 – 1 et τα1 + β1 – 1.

Trois cas sont envisageables selon que le taux de couverture affecte ou non le signe de τα1 + β1 – 1. Le premier cas, qui est représenté par le graphique 1a concerne la situation de la petite nation totalement ouverte sur l’extérieur lorsqu’elle est structurellement créancière. Les deux cas suivants, décrits par les graphiques 1b et 1c détaillent le comportement d’une petite économie structurellement débitrice. Le premier de ces deux cas suppose un taux de couverture qui conduit au respect du critère des élasticités critiques. Le dernier cas envisage un taux de couverture tellement réduit que le critère amendé des élasticités critiques n’est plus vérifié.

Considérons d’abord le cas où le taux de couverture excède strictement l’unité (c’est-à-dire τ > 1). Les signes des pentes (BB) et (BC) sont identiques, mais en raison d’un taux de couverture supérieur à l’unité, la pente de (BB) est inférieure en valeur algébrique à celle de (BC). Ce premier cas est décrit dans le graphique 1a. À la suite de ce choc qui affecte le bas de la balance des paiements, la droite (BB) glisse vers le haut. Le nouvel équilibre passe de E0 à E1 et cela correspond à des taux de croissance du revenu domestique réel et du taux de change réel supérieurs aux rythmes de croissance initiaux. La contrainte d’équilibre qui pèse sur les comptes extérieurs rend nécessaire un ajustement de l’excédent courant afin de compenser le déséquilibre lié à l’arrêt des flux de capitaux. L’un des moyens disponibles, compte tenu de la position structurellement créditrice de l’économie, est d’adopter une politique d’augmentation du rythme de croissance du revenu domestique réel. Cette action augmente le volume des importations domestiques. À volume constant des exportations, le solde courant se détériore. Le marché des changes est déstabilisé ce qui déprécie le taux de change nominal, donc le taux de change réel. La dépréciation supplémentaire du taux de change réel améliore la compétitivité internationale de l’économie, ce qui affecte à nouveau les comptes extérieurs et autorise alors une augmentation supplémentaire du rythme de croissance du revenu domestique réel.

Graphique 1

A

Modèle BB-BC : (τ > 1)

Modèle BB-BC : (τ > 1)

B

Modèle BB-BC : ((1 – β1) / α1 < τ < 1)

Modèle BB-BC : ((1 – β1) / α1 < τ < 1)

C

Modèle BB-BC : (τ < (1 – β1) / α1))

Modèle BB-BC : (τ < (1 – β1) / α1))

-> Voir la liste des figures

L’enjeu est de distinguer l’action relative du taux de change réel et du revenu domestique réel sur les comptes extérieurs. Ces influences dépendent de la sévérité de la contrainte extérieure, c’est-à-dire de la pente de (BC). Lorsque les élasticités-prix du commerce extérieur de cette économie créancière sont peu élevées, la pente de la droite (BC) est proche de la verticale. Ce contexte précis de faibles élasticités-prix du commerce extérieur applicable à des pays créanciers a une forte incidence sur les choix de politique économique des autorités nationales. Un objectif donné dans le rythme de croissance du revenu domestique réel compatible avec ce nouvel équilibre de la balance de base ne peut se réaliser qu’au prix d’une grande instabilité du taux de change nominal en imposant des modifications nettement plus importantes du taux de change réel.

Maintenant, lorsque cette nation de petite taille dispose d’un taux de couverture inférieur à l’unité, il s’agit d’une économie structurellement débitrice. Il est possible d’envisager deux cas de figures puisque la pente de (BB) peut devenir négative lorsque la valeur retenue du taux de couverture est particulièrement réduite. Les effets sur l’équilibre extérieur, ainsi que sur les rythmes de croissance du taux de change réel et du revenu domestique réel qui dépendent de la position de (BB) vis-à-vis de la droite (BC) peuvent alors être nettement différenciés. Les nations subissent différemment les effets d’une variation soudaine des flux nets de capitaux sur leur rythme de croissance d’équilibre du revenu domestique réel et de la parité réelle.

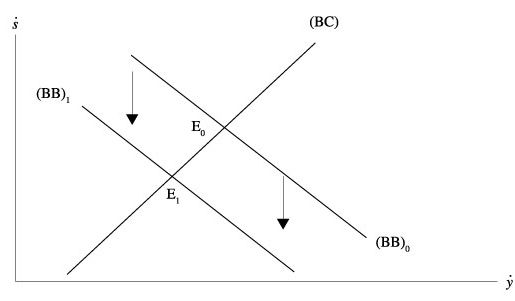
Considérons d’abord le cas où le taux de couverture est inclus dans l’intervalle ](1 – β1) / α1, 1[. Ce cas est décrit par le graphique 1b. La configuration des élasticités se traduit par des pentes de droites (BB) et de (BC) qui restent du même signe, puisque le critère des élasticités critiques amendé demeure vérifié. Lorsque l’économie subit ce choc exogène, l’apparition du déséquilibre extérieur fait glisser la droite (BB) vers le haut. Le passage de BB0 à BB1 caractérise un couple (ẏ,ṡ) qui est différent de l’équilibre initial. L’équilibre se situe au point d’intersection E1 des droites (BC) et (BB)1 qui décrit une situation où le rythme de croissance d’équilibre du revenu domestique réel et le rythme de dépréciation réelle sont plus faibles. Les rythmes de croissance d’équilibre du revenu domestique réel et du taux de change réel doivent s’ajuster à la suite de l’arrêt brutal des flux de capitaux. Cela nécessite une réduction du rythme de croissance du revenu domestique réel. La réduction du volume des importations qui est induite améliore la balance courante. Le marché des changes est déséquilibré, puisque le redressement du solde courant peut conduire à des achats de monnaie nationale sur le marché des changes. Le taux de change nominal s’apprécie, ce qui pèse sur le rythme de croissance du taux de change réel. La modification induite de la compétitivité-prix à l’international conduit à une nouvelle modification du solde courant. Le rythme de croissance du revenu domestique réel doit alors se réduire à nouveau pour devenir compatible avec les comptes extérieurs. L’importance des modifications de ces deux rythmes de croissance d’équilibre dépend, là encore, de la pente de la droite (BC).

La pente de la droite (BC) apparaît cruciale puisqu’elle conditionne l’incidence de la variable de revenu domestique réel sur la variable de taux de change réel. En effet, lorsque l’association des élasticités-prix du commerce extérieur et du taux de couverture génère une droite (BC) proche de l’horizontale, alors le taux de croissance du taux de change réel sera inférieur au taux de croissance du revenu domestique réel à la suite d’un choc exogène sur la balance des paiements. L’essentiel de l’ajustement transite par une variation du rythme de croissance du revenu domestique plutôt que par une variation du rythme de croissance du taux de change réel. Le coût en termes de dépréciation accélérée du taux de change réel sera relativement plus faible lorsque la pente de (BC) est proche de l’horizontale et relativement plus important lorsque la pente de la droite (BC) est proche de la verticale. Implicitement, une économie répondant à cette première configuration d’élasticités-prix peut avoir une incitation d’autant plus forte en faveur d’une politique de stabilisation du taux de change nominal que l’impact d’une variation supplémentaire du rythme de croissance du revenu domestique réel induit une variation du taux de change réel nettement moins importante. Par contre, l’action sur le taux de croissance du revenu domestique réel s’avère nettement plus importante. Il y a donc bien deux effets qui s’opposent et le passage de E0 vers E1 ne peut se réaliser qu’en admettant que les effets transitent essentiellement par le revenu plutôt que par les actions sur le taux de change réel. Mais lorsque la droite (BC) de cette économie débitrice est plus importante, alors la nation subit une variation relativement plus forte de son taux de change réel à la suite de l’arrêt brutal des afflux de capitaux compatible avec l’équilibre de la balance de base. Cette situation peut caractériser les économies qui subissent des variations significatives du rythme de croissance du taux de change réel à la suite d’importantes sorties nettes de capitaux. Ces dernières favorisent en retour l’amélioration de la compétitivité puisque les deux critères d’élasticités critiques demeurent respectés.

En dernier lieu, envisageons le cas où le taux de couverture est inférieur à (1 – β1) / α1. Il s’agit toujours d’une économie structurellement débitrice, mais la situation diffère de la précédente car le signe de la pente de (BB) devient négatif alors que celui de (BC) demeure positif. Les effets sur l’équilibre extérieur, ainsi que sur les rythmes de croissance du taux de change réel et du revenu domestique réel, qui dépendent de la position relative de (BB) vis-à-vis de la droite (BC), sont alors différents, puisque le théorème des élasticités critiques amendé par le taux de couverture est invalidé.

Le long de (BB), l’accélération du rythme de croissance du revenu domestique réel s’associe à une réduction du rythme de croissance du taux de change réel. Cependant, la réduction du rythme de croissance du taux de change réel génère un excédent courant au lieu d’un déficit courant. Le rythme de croissance du revenu domestique courant doit alors augmenter afin de peser sur le solde courant, par l’intermédiaire de l’augmentation des importations afin de favoriser le retour vers l’équilibre extérieur.

Dès lors, l’effet induit par l’arrêt brutal des afflux de capitaux se traduit par un déplacement vers le bas de la droite (BB), en raison du déséquilibre soudain des comptes extérieurs. Le taux de croissance du taux de change réel se réduit. Mais à l’inverse de l’économie structurellement créancière, le rythme de croissance du revenu domestique réel compatible avec ce nouvel équilibre extérieur doit aussi se réduire puisque l’appréciation réelle du taux de change n’a pas l’effet escompté sur le solde courant. Dès lors, une économie structurellement débitrice dont le critère de Marshall-Lerner amendé n’est plus validé, notamment parce qu’elle dispose d’un taux de couverture excessivement réduit, doit essentiellement se concentrer sur les actions affectant le rythme de croissance du revenu domestique réel plutôt que celui du taux de change réel lorsqu’elle est confrontée à un arrêt soudain dans ses afflux de capitaux. L’invalidation du critère de Marshall-Lerner amendé rend illusoire toute stratégie active de modification du change. L’équilibre extérieur est restauré principalement par une variation du rythme de croissance du revenu domestique réel, sans que cela n’affecte fortement le taux de change réel. Les autorités ont intérêt à adopter des mesures de réduction du rythme de croissance du revenu domestique réel. Cette action est susceptible de résoudre, par l’intermédiaire de la réduction des importations, le cercle déficit courant croissant et dépréciation réelle continue. L’efficacité de ces actions sur le rythme de croissance du revenu domestique réel peut apparaître d’autant moins difficile à mettre en application que la pente de la droite (BC) est proche de l’horizontale.

Cette troisième configuration s’oppose fortement à la première où l’absence de préoccupation directe en matière de change nominal pouvait apparaître comme l’alternative idéale dont les autorités pouvaient aisément tirer partie. Cette passivité des autorités domestiques en matière de change était alors directement conditionnée par la spécialisation internationale qui leur offrait ainsi la possibilité de ne pas intervenir sur le marché des changes, ou du moins à une moindre échelle.

Conclusion

Cet article a tenté de montrer que les travaux contemporains qui se préoccupent du lien entre les ajustements rapides des comptes extérieurs, du taux de change réel et de la croissance économique, doivent aussi mettre l’accent sur les taux de croissance des variables, comme le taux de change réel ou le revenu réel.

Une analyse théorique portant sur les mouvements conjoints du taux de change réel et du revenu domestique réel compatible avec l’équilibre a donc été développée. Elle mobilise le modèle postkaldorien de Thirlwall (1979) où la croissance du revenu domestique réel est contrainte par la nécessité d’assurer l’équilibre de la balance courante. Ce modèle fait l’objet d’innovations qui permettent d’élaborer deux blocs d’équilibre partiels. Le premier précise le rythme de croissance du taux de change réel compatible avec un taux de couverture constant. Le second incorpore explicitement les flux de capitaux et décrit le rythme de croissance du taux de change réel compatible avec l’équilibre courant que compensent des flux nets de capitaux de long terme. L’articulation de ces deux blocs permet de déduire le taux de croissance d’équilibre du taux de change réel et le taux de croissance d’équilibre du revenu domestique réel. Ils sont uniques.

À moyen terme, les valeurs des élasticités du commerce extérieur et plus particulièrement celles relatives aux prix ainsi que le taux de couverture conditionnent fortement la situation extérieure d’une économie et ses modalités d’ajustements à un choc extérieur, comme un arrêt brutal dans les afflux de capitaux. L’économie structurellement créditrice, notamment parce que son taux de couverture est élevé, et dont les élasticités-prix du commerce extérieur apparaissent relativement importantes peut avoir plus d’incitation pour adopter une stratégie de faible dépréciation, voire de stabilisation de la parité. Ce cas illustre bien la position de certains pays d’Asie du Sud-Est durant les années quatre-vingt lorsqu’ils dégageaient des surplus commerciaux significatifs alors qu’une large part de leur production manufacturière se positionnait dans le bas de gamme, c’est-à-dire essentiellement des produits où les élasticités-prix sont importantes.

Par contre, l’économie débitrice dont le taux de couverture est particulièrement réduit voit ses choix de politiques économiques contraints par sa situation extérieure. Les autorités nationales doivent adopter prioritairement des politiques agissant sur le rythme de croissance du revenu domestique réel puisque l’action du taux de change sur les comptes extérieurs mène à des ajustements pervers. Certains pays en développement, comme les pays producteurs de matières premières, répondent à ce cas, car ils subissent des déséquilibres extérieurs durables. La dépréciation du taux de change n’est d’aucun effet durable sur la croissance et ne permet pas d’affecter favorablement leur spécialisation internationale car le taux de couverture est insuffisamment élevé pour assurer le respect du critère des élasticités critiques amendés. Enfin, l’économie qui se situe dans une position intermédiaire doit mettre l’accent sur des stratégies de spécialisation où les élasticités-prix du commerce extérieur sont importantes. Elle est alors susceptible d’intégrer plus aisément une zone où le rythme de croissance du taux de change nominal est réduite, limitant les effets pervers des modifications du change réel surtout si le taux de couverture est amené à se réduire.