Résumés
Abstract
Rapid advances in data analysis techniques—particularly for predictive algorithms—have opened the door for radically new perspectives on legal practice and access to justice. Several firms in North America, Asia, and Europe have set out to use machine-learning techniques to generate legal predictions, raising concerns regarding ethics, reliability and limits on prediction accuracy, and potential impact on case law development. To explore these opportunities and challenges, we consider in depth one of the most litigated issues in Canada: wrongful termination disputes and, more specifically, the question of reasonable notice determination. Beyond the thorough analysis of this question, this paper is also intended to act as a road map for non-technicians (and especially lawyers) on the application of artificial intelligence (AI) methods, illustrating both their potential benefits and limitations in other areas of dispute resolution.
To achieve these results, we first created a large dataset by annotating historic cases related to employment termination. This dataset proved useful for assessing the predictability of reasonable notice of termination, that is, the accuracy and precision of AI predictions. In particular, it helped identify the degree of inconsistency in notice period cases, incidentally exposing the limitations of legal predictions. We then developed predictive algorithms to estimate notice periods based on details of the employment period and investigated their accuracy and performance. Moreover, we thoroughly analyzed these algorithms to better understand the judicial process, and in particular to quantify the weight and influence of case-specific features in the determination of reasonable notice. Finally, we closely analyzed cases that were poorly predicted by the algorithms to understand the judicial decision-making process and identify inconsistencies—a strategy that will ultimately yield a deeper practical understanding of case law.
This project will open the door to the development of an access-to-justice project and will provide users with an open-access platform for employment legal help (www.MyOpenCourt.org).
Résumé
Les progrès rapides des techniques d’analyse de données — les algorithmes prédictifs en particulier — ont ouvert la porte à des avenues radicalement nouvelles en matière de pratiques juridiques et d’accès à la justice. Plusieurs cabinets d’avocats d’Amérique du Nord, d’Asie et d’Europe ont entrepris d'utiliser des techniques d’apprentissage statistique (machine learning) pour prédire et générer des conclusions d’ordre juridique, ce qui soulève des préoccupations concernant l’éthique, la fiabilité et les limites de la précision de ces conclusions, ainsi que leur impact potentiel sur le développement de la jurisprudence. Pour explorer ces possibilités et ces défis, nous examinons en profondeur l’une des questions les plus litigieuses au Canada : les licenciements abusifs et, plus particulièrement, la question de la détermination du préavis raisonnable. Au-delà de l’analyse approfondie de cette question, cet article se veut également une feuille de route pour les non-techniciens (et surtout les avocats) sur l’application des méthodes d’intelligence artificielle (IA), illustrant à la fois leurs avantages potentiels et leurs limites dans d’autres domaines de la résolution des litiges.
Pour atteindre cette fin, nous avons d’abord colligé un vaste ensemble de données en annotant les cas historiques de congédiement injustifiés. Cet ensemble de données s’est avéré utile pour évaluer la prévisibilité d'un préavis raisonnable de licenciement, c’est-à-dire la précision des prédictions de l’IA. En particulier, cette approche permet de déterminer le degré d’incohérence et de variation des cas de préavis, en exposant incidemment les limites de ses conclusions légales. Nous avons développé des algorithmes prédictifs afin d’estimer les délais de préavis en fonction de la durée de l’emploi et avons étudié leur précision et leur performance. De plus, nous avons procédé à une analyse approfondie de ces algorithmes afin de mieux comprendre le processus judiciaire, et en particulier de quantifier le poids et l’influence des caractéristiques propres à chaque affaire dans la détermination du préavis raisonnable. Enfin, nous avons analysé de près les cas mal prédits par les algorithmes d’IA afin de mieux comprendre le processus décisionnel judiciaire et d’en déterminer les incohérences — une stratégie qui permettra en définitive d’approfondir la compréhension pratique de la jurisprudence.
Ce projet ouvre la voie au développement d’un projet d'accès à la justice à plus grande échelle et fournira aux utilisateurs une plateforme en libre accès d’aide juridique en droit du travail (www.MyOpenCourt.org).
Corps de l’article
Introduction
Machine learning, or artificial intelligence (AI), relies on computing capabilities to analyze and extract patterns within vast amounts of information, and to derive statistical models from these patterns to predict associations between features and outcomes. For the field of law, these techniques offer opportunities for developing predictive tools capable of evaluating the odds of winning cases[1] or estimating damages.[2] From a theoretical standpoint, the application of AI in law has the potential to shed new light on how legal decisions are made by illuminating the evolution of case law and the consistency (and predictability) of judicial decisions.[3] Moreover, providing access to efficient AI systems could create invaluable tools for improving access to justice, currently a prominent issue in North America.[4] From a practical standpoint, AI systems would provide critical information for litigants insofar as determining litigation outcomes is key in helping them decide whether they should settle or litigate, by enabling them to identify their Best Alternative to a Negotiated Agreement (BATNA).[5] It is important to note, however, that while the prospect of applying AI in the legal field has come with high expectations, it has also raised important ethical concerns,[6] in particular regarding the reliability[7] and explicability of predictions.[8]
Accordingly, this piece is intended to present an overview of the application of AI and statistical methods to legal data, and more particularly to the determination of reasonable notice for workplace dismissals. It will build on previous statistical studies that have attempted to decipher judicial logic regarding the determination of notice.[9] That said, it is important to note that machine learning and statistical techniques are not applicable to every sub-field of law. The most promising areas are legal questions in which the court’s determination lends itself to identifying a discrete set of factors, and for which sufficient historical data exist. In this regard, notice calculation seems particularly well suited to the application of data science insofar as it is a fact-driven area that relies on a set of factors defined by a landmark case (Bardal).[10]
We have therefore explored in depth the predictability of notice determination in order to give insight into the judicial process. To this end, we have constructed an extensive dataset of wrongful termination employment cases in Canada. The database is structured around legally relevant factual predictors—the features that judges take into consideration in determining notice and that are available prior to the formulation of any judgement. This extraction and normalization of features from legal texts into a predefined structured data source opens the way to data analysis and the conception of predictive algorithms. For each case, we gathered a variety of factors, including all the well-known Bardal factors—namely character of employment, age, duration, availability of other employment, experience, and qualifications—as well as external factors, such as the name of the judge, the employment industry, and the gender of the employee.
The project sought to answer a set of predictive and descriptive questions. Specifically, we focused on three main sets of questions: (1) What is the predictability of notice periods? How precise and accurate can predictions be? What is the percentage of total outcomes predicted correctly? What is the uncertainty of these predictions? (2) Can AI help identify the relative weight of the factors taken into consideration by judges and the way each factor contributes to the notice period determination? and (3) Can AI help to identify inconsistencies in case law?
This paper is embedded into a wider endeavour aimed at developing an open access prediction project for employment litigation in Canada, with the ultimate goal of improving access to justice for all individuals.[11] The project is conducted by the Conflict Analytics Lab, a consortium focused on the application of AI to dispute resolution, established in 2018 as a forum for collaboration between academic institutions and industry partners (including Brandeis University, Columbia University Business Analytics, HEC Paris, and McGill University). The Conflict Analytics Lab grew out of the Queen’s University Faculty of Law and Smith Business School in Canada. The goal of the lab is to leverage data science and computing expertise to develop research-based applications in the field of dispute resolution. An interdisciplinary team of faculty members,[12] graduate analytics students, computer science students,[13] and law students participate in this project via the Conflict Analytics Practicum,[14] a year-long project commissioned by the lab and industry partners that focuses on conflict-related data problems.
This research is drawn from a larger project aimed at developing an open-source system for small-claims disputes[15] (including employment disputes) that is based not only on legal trends, but also on negotiation data.[16] This predictive system—MyOpenCourt.org—aims to promote access to justice in small claims courts and provide legal help to self-represented litigants by democratizing legal analytics technology. The system would provide a degree of legal support for self-represented litigants by helping them determine the likely outcome of pursuing their matter in court.[17]
The remainder of this paper describes in detail the data collection process: our methods for extracting features for our text and building a predictive model (Part I); our analytical methods for describing case law and evaluating the predictive power of machine-learning algorithms for notice determination (Part II); and finally, the analytical power of AI models and whether they can help to determine levels of inconsistency in reasonable notice cases (Part III).
I. Method of Data Collection
Our algorithmic study builds upon the development of a structured, extensive database of notice period cases. In this section we present the methods we used to build the database (Part I.A) and the composition of the database (Part I.B), and provide basic analyses aimed at identifying how relevant features impact judges’ decisions (Part I.C).
A. Legal Text Mining
The text mining technique aims at quantitatively assessing and comparing cases and legislative frameworks across a given sample. There is a growing body of literature on the application of modern text mining techniques to unstructured text data in many different fields, legal texts among them.[18] While these techniques have allowed significant progress, the extraction of insightful legal and negotiation data has not been successfully automated to date. Accordingly, we undertook an intensive data collection and annotation process. We gathered a team of legal analysts at Queen’s University Faculty of Law who invested significant effort in the collection, organization, and harmonization of the legal and non-legal factors relevant to determining notice periods.[19]
The calculation of notice periods is in principle governed by a set of objective factors established by the precedent-setting Bardal case.[20] Specifically, if the employment relationship is governed by an indefinite contract and the employer wishes to terminate the employment relationship for any reason (that is not discriminatory), then the employer has the obligation to provide notice or pay in lieu of notice, calculated according to the Bardal system.[21] Accordingly, violations of this obligation arise from failure to provide sufficient notice or pay.[22] When a former employee believes they have been terminated without sufficient notice or pay and decides to pursue the matter in court, a court must attempt to determine what compensation the employee would have received had adequate notice been provided and award damages for that loss (less any mitigation income). Courts typically begin their analysis of what constitutes “reasonable notice” by looking at the so-called Bardal factors:
The reasonableness of the notice must be decided with reference to each particular case, having regard to the character of the employment, the length of service of the servant, the age of the servant and the availability of similar employment, having regard to the experience, training and qualifications of the servant.[23]
For our purposes, we have collected fourteen features (including the Bardal factors) to be considered whenever available. These include the following:[24]
-
General information associated with the case (court, province, judge’s name, and year of judgment);
-
Personal information about the claimant (gender and race);[25]
-
Facts related to the claimant’s employment (industry and job title);
-
The Bardal factors (duration of employment, age of the claimant, availability of similar employment, managerial or operational character of employment, experience, and qualifications); and
-
Court judgment (decision of the court in terms of months of notice period).
The data collected by the legal analysis was accessed using Westlaw. Analysts thoroughly read the cases and extracted the above-listed information. To consistently assess qualitative elements such as employee qualification, experience, and availability of similar employment, a scale was provided to the analysts with criteria to help them categorize each case in up to five classes.[26]
B. Composition of the Database
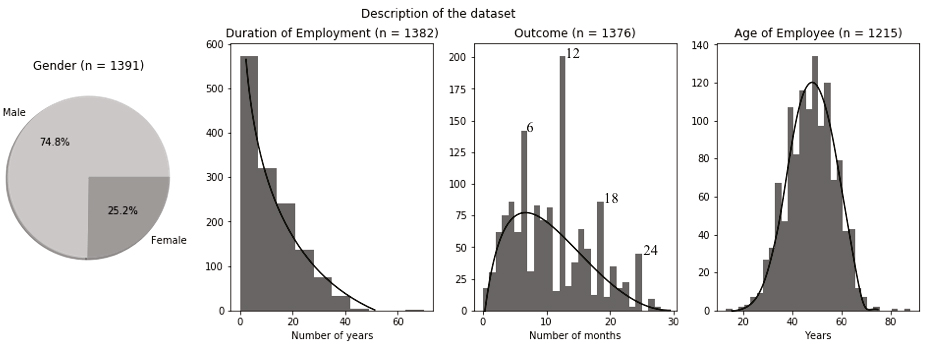
We found a total of 1,391 cases relevant to notice calculation in Westlaw. Figure 1 (below) summarizes the content of the database that we were able to build using the information extracted from these cases. We noticed a significant gender imbalance in the case law examined: almost three out of every four claimants (73.9 per cent) were identified as male (Figure 1, left). The ages of the claimants ranged from twenty to over eighty years old, with an average claimant age of 47.4 years and a standard deviation[27] of 9.7 years, associated with a bell-shaped distribution (Figure 1, right). The duration of the claimants’ employment ranged from less than a year to forty years, with more cases associated with longer durations (456 were less than five years in duration, and 266 cases were between five and ten years; see Figure 1, middle left). The median[28] duration of employment was nine years, with a median absolute error of eight years.
Employment availability (score 1–5)[29] showed a bell-shaped distribution[30] with an average employment availability equal to 2.96 and a standard deviation of 1.1. Remarkably, no imbalance was found based on the character of employment: the database was split almost equally between managerial and operational workers. Experience and qualification were found to be almost uniformly distributed between 1 and 5, indicating no imbalance in the case law based on these criteria.
As expected, we found that available data reflected the overall distribution of the population in Canadian provinces (barring Quebec, which was not included in the analysis because of its distinct civilian legal system). The majority of cases were decided in Ontario (40 per cent), followed by British Columbia (27 per cent), Alberta (11 per cent), Saskatchewan and New Brunswick (5 per cent each), and Nova Scotia (4 per cent), with the remaining provinces contributing less than 4 per cent of cases.
In the cases considered, the notice periods awarded by the courts ranged in length from one to about thirty months (Figure 1, middle right), with a median notice period of ten months and a median absolute error of 5.15 months. Interestingly, a few notable durations seem to stand out from the distribution at twelve (mode[31] of distribution, 15 per cent of judgments), six (9.5 per cent), eighteen (7 per cent), and twenty-four months (3 per cent), potentially corresponding to a bias toward clearly relatable durations for the judge and the parties.
Figure 1
Description of the dataset. From left to right: Gender distribution and histograms for duration of employment (in years), notice period (hereafter, outcome) with peaks at 6, 12, 18 and 24 months highlighted, and claimant age (bell-shaped curve centred at 47 years). Idealized smooth profile drawn in black.
C. Inherent Fluctuations in Notice Calculation
The success of the application of predictive analytics to judicial data is very much dependent on the size and quality of the dataset, but also on the degree of consistency inherent in the decision-making process. Accordingly, before engaging in predictive analytics, we have analyzed the intrinsic consistency of the case law. To this end, we extracted subsets of cases sharing similar characteristics in order to highlight the variations in notice determination across the dataset.
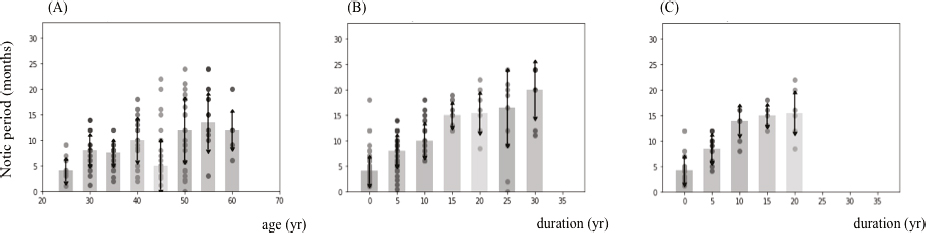
Figure 2
Notice period data points for relatively highly qualified operational workers (qualification score 4): as a function of age, all durations together (A); as a function of employment duration, all ages together (B); or for workers aged 40–50 years old (C).[32] Each circle represents one data point (i.e., one decision) and the height of the associated bar is the median notice period. Variations around this averaged decision give a sense of the fluctuation (vertical bar: MAD) of the outcome.[33]
Figure 2 in particular shows the distribution of notice periods across the cases considered that involved operational workers with a qualification score of 4 (subset of cases shown in Figure 3, below);[34] each circle represents each individual case[35] as a function of the age of the employee (A) or as a function of employment duration (B and C), for all workers (B) or only for workers aged between forty and fifty years old (C). These graphs illustrate quite strikingly that while duration of employment clearly emerges as a determining factor for the calculation of notice, there are major variations across the case law. For instance, in Figure 2A, we observed that for each age category the difference between the shortest and longest notice period was systematically larger than one year. While much less fluctuation was found when gathering cases based on duration of employment (as shown in Figure 2B), we still observed major fluctuations in notice periods: operational workers with a qualification score of 4 who were employed for zero to five years still obtained notice periods ranging all the way from one to eighteen months (seventy-three cases were considered, with a median absolute deviation of 2.45).
Similar amplitudes of fluctuation were found for other duration ranges as well. For employment durations of five to ten years, notice periods ranged between 0.5 and fourteen months (forty-four cases were considered, with a median absolute deviation of 2.74 months). Other ranges of employment durations were typically associated with amplitudes in notice periods of more than one year, with median absolute deviations typically above three months. Fixing both age and duration did not solve this problem (as shown in Figure 2C) and major fluctuations of several months remained, although the number of cases corresponding to each combination of criteria was much lower (and thus results may be statistically less significant).
Figure 3 (below) offers a broader picture by considering all data points for both managerial and operational workers, at all qualification levels (1–5) and either as a function of employee age within a five-year window (top panels) or as a function of employment duration (middle and bottom panels). As in Figure 2, all combinations yielded significant fluctuations in the length of notice periods (between two and three months, on average).
We conclude that while some clear trends can be observed in notice periods, including in particular an expected increase in notice period depending on duration of employment, the level of fluctuation in notice periods is significant, with amplitudes often above six months and median absolute deviations of more than 2.5 months. In light of the level of fluctuation observed across the dataset, it is possible to argue that it will be difficult to build a model capable of predicting the notice value with precision of less than one month.[36]
Figure 3
Notice period data points as a function of age, all durations together (top panels), or as a function of employment duration, all ages together (middle) or for workers aged 40–50 years old (bottom), split into operational or managerial workers and as a function of employment qualification. Same convention as in Figure 2.
II. Predictability of Reasonable Notice Calculation
This section will discuss how machine-learning research can help to determine claimants’ BATNA and what a terminated employee could expect to be awarded by a court. Machine-learning techniques will analyze statistics of past cases to “learn” an association between case features (i.e., the Bardal factors and other elements) and outcomes for notice period.[37]
A. Selecting Relevant Criteria and Identifying Correlated Attributes
In order to develop a predictive system for notice calculation, we begin by analyzing the relative impact of each Bardal factor for the notice period. It would be difficult indeed to attempt a prediction if cases were decided by judges irrespective of Bardal criteria or with no consistent method of calculating notice. If judges do calculate notice in a consistent manner with respect to Bardal criteria, correlations will be found between notice periods and these criteria. If correlations are indeed found, then we need to quantify the weight of each variable in order to build a model that reflects the reality of judicial calculations.
To that end, we first identified the features that showed the highest correlation with judges’ decisions (Figure 4, below), using Pearson’s correlation coefficients between all variables and the notice period.[38] Technically, Pearson’s correlation coefficients[39] quantify the degree to which two variables are correlated: coefficients close to 1 show highly correlated variables, coefficients close to 0 are found for uncorrelated variables, and negative coefficients indicate variables that vary together but in opposite directions. For instance, the positive Pearson’s correlation coefficients between employment duration and notice period indicate that the longer the duration of employment, the longer the notice period awarded. In contrast, the negative correlation between employment availability and notice period indicates that notice periods are shorter for cases with high employment availability.
Figure 4
Correlation (Pearson’s coefficient) between variables and with the notice period decided by the judge. For categorical variables, we adopted the following conventions: gender (1 for male, 2 for female); character of employment (1 for managerial, 2 for operational).
Large correlations between notice period and duration of employment (77 per cent), experience (48 per cent), and age (40 per cent) were found, together with a 25 per cent anti-correlation with character of employment (suggesting, with our conventions, that managerial employees obtain longer notice periods than operational employees). Between variables (dashed boxes), correlations were found between age, duration, and experience. A negative correlation was found between character of employment and qualification, suggesting lower qualifications for operational workers than for managers.
The factor correlating most strongly with notice period was found to be duration of employment (77 per cent positive correlation). This highlights the major impact that length of service has in a judge’s determination of how much notice should be awarded: the longer an employee has worked with a company, the longer the notice period awarded tends to be. Employee experience and age follow in terms of importance (correlating at 48 per cent and 40 per cent, respectively), but both factors also show strong correlations with employment duration (45 per cent and 40 per cent respectively). This creates some ambiguity as to which factor exerts the most influence on notice outcomes. Employees who have worked for longer durations are generally older and have consolidated more experience than those with shorter employment durations, so the correlation observed between these factors and the outcome could be due to employment duration only. The character[40] of employment and employment availability also shows smaller yet relatively significant negative correlations with the outcomes. These correlations highlight the fact that shorter notice periods tend to be awarded if similar employment is available or if the employee is less qualified. Again, these items show some level of correlation with employment duration that will be deciphered using our algorithms.
B. Predicting Notice Periods Based on Length of Service
The strong correlation observed between notice outcome and employment duration is consistent with past empirical studies that have reported length of service to be the strongest predictor of reasonable notice determinations.[41] In particular, Kenneth Thornicroft found a strong correlation between notice awards and tenure with a Pearson correlation coefficient between the final notice award and tenure of 0.816, suggesting that the rule of thumb is far from being dead.[42] Furthermore, employees with fifteen years of service or more, as a group, received notice awards 7.6 months longer than those of employees with five to fifteen years of service.[43]
Thornicroft’s empirical results suggest a linear relationship between duration of employment and notice period. In mathematical language, this means that the notice period T can be deduced from the employment duration D through a formula of type
![]()
where the coefficient α would be the typical number of additional months of notice period per year of service, estimated by Thornicroft to be around 0.5 months per year of service. The intercept β is an offset parameter.
In machine learning, the process of finding such linear relationships is called a
linear regression.[44] Let us denote by N the number of data
points available and ![]() the duration of employment and notice period for case
the duration of employment and notice period for case ![]() in our dataset. Ordinary least square regression was used to identify the
regression parameters α and β that minimize the average error (across a training
set, a randomly chosen subset of the full database) between the actual notice period
Ti and a predicted value
in our dataset. Ordinary least square regression was used to identify the
regression parameters α and β that minimize the average error (across a training
set, a randomly chosen subset of the full database) between the actual notice period
Ti and a predicted value
![]() through the linear model. We used the implementation provided in the
Scikit-Learn Python package.[45]
through the linear model. We used the implementation provided in the
Scikit-Learn Python package.[45]
In order to validate the statistical analysis, we first trained our algorithm on
the data and assessed the precision of the predictions of the algorithm on cases that were
not used in the learning process. To this purpose, we split the data into a training set
(80 per cent of the cases) and a test set (20 per cent of the cases). The accuracy of our
algorithms will be expressed in terms of the average error made in the predictions of all
cases of the validation (test) set, namely cases that were not used to train the
algorithm. To estimate the accuracy of precision of our predictions, we will provide the
median absolute error, that is the median error of prediction ![]() on the training set, as well as estimates of the dispersion of the
distribution of prediction errors through the quantiles of the error distributions
(namely, the durations
on the training set, as well as estimates of the dispersion of the
distribution of prediction errors through the quantiles of the error distributions
(namely, the durations ![]() and
and ![]() corresponding to the first 25 per cent of cases, 50 per cent of cases, and
75 per cent of cases respectively).
corresponding to the first 25 per cent of cases, 50 per cent of cases, and
75 per cent of cases respectively).
In line with Thornicroft’s analysis, we found that the optimal fitted parameters
for a linear model correspond to ![]() months per year of service, consistent with the observation that each
additional year of employment corresponds to two additional weeks in the notice period.
The best offset found was given by
months per year of service, consistent with the observation that each
additional year of employment corresponds to two additional weeks in the notice period.
The best offset found was given by ![]() months. Both estimates are associated with significantly lower standard
deviation compared to the mean (for the slope α, a standard deviation of 0.016, and for the offset, 0.24 months),
confirming the significance of this fit. In particular, the t-statistics for the slope
coefficient α and for the intercept
β are high (22.49 and 33.03, respectively)
and confidence intervals narrow (99 per cent confidence intervals [0.46, 0.54] and [4.74,
5.98] respectively). This trend emphasizes the high statistical significance of the fits
(p-value smaller than 0.1 per cent) and thus the strong linear relationship between
duration of employment and notice period. Also, it is worth noting that these results
confirm that the rule of thumb—one month’s notice per year of service—is not applied by
judges (see Figure 5, below).[46]
months. Both estimates are associated with significantly lower standard
deviation compared to the mean (for the slope α, a standard deviation of 0.016, and for the offset, 0.24 months),
confirming the significance of this fit. In particular, the t-statistics for the slope
coefficient α and for the intercept
β are high (22.49 and 33.03, respectively)
and confidence intervals narrow (99 per cent confidence intervals [0.46, 0.54] and [4.74,
5.98] respectively). This trend emphasizes the high statistical significance of the fits
(p-value smaller than 0.1 per cent) and thus the strong linear relationship between
duration of employment and notice period. Also, it is worth noting that these results
confirm that the rule of thumb—one month’s notice per year of service—is not applied by
judges (see Figure 5, below).[46]
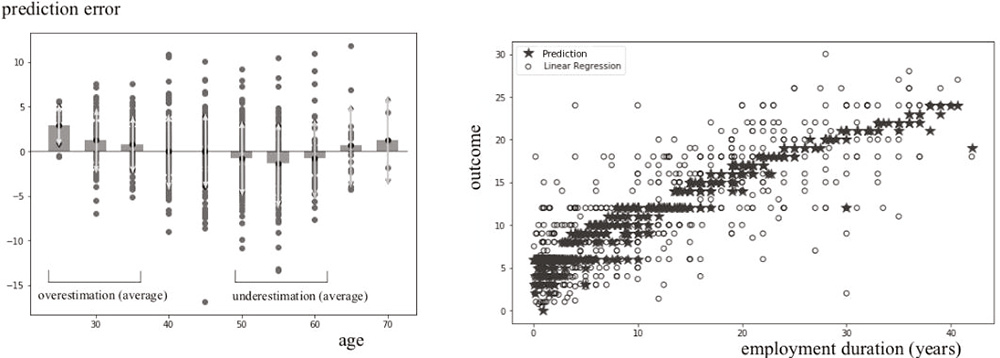
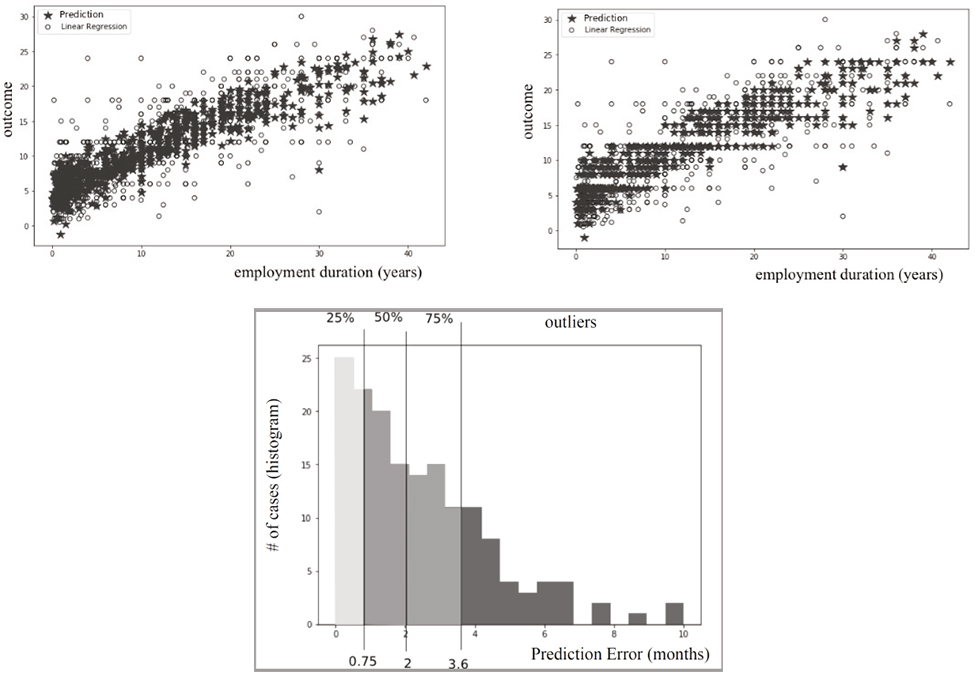
Figure 5
Ordinary least square regression to a linear (A) or polynomial (B) function of employment duration only. Empty circles are data points; black stars are predictions (corresponding to the closest integer associated with the linear or polynomial formula); and solid lines show a continuous model (linear or polynomial). The dashed line in (A) corresponds to the rule of thumb. The bottom figure shows the error analysis for each model and in particular the median error of 2.36 and 2.25 months respectively.
An overall good visual agreement is found between the data and the linear model (Figure 5). Despite the simplicity of the model, we found that the linear model achieves similar fluctuations to the intrinsic variations in notice period found in Part I.B. In particular, we found that on the validation set, the model predicts notice periods with a median error of 2.36 months (standard deviation of error 2.2). Put another way, in more than 50 per cent of cases, the algorithm predicted the notice award accurately to within 2.36 months. Twenty-five percent of the predictions were accurate to within 1.14 months, and 75 per cent were accurate to within four months. This is comparable to the 2.5 months of intrinsic fluctuations found, for instance, for all workers with a fixed age range (40–50 years old), qualification, character of employment, and employment duration.[47]
To improve the predictions and take into consideration potential nonlinear dependencies between duration of employment and notice periods,[48] we used ordinary least square regression to identify polynomial relationships of type
![]()
where p denotes the degree of the polynomial and, as before, T is the notice period and D the employment duration.[49] We observe in Figure 5 that the prediction follows the data variation nicely and reproduces the saturation effect for longer employment durations—that is, the increase in notice period is faster for smaller durations. This model reduces the prediction error with respect to the validation set by only a small amount, bringing it down to 2.22 months (standard deviation 2.21) with 25 per cent of cases accurately predicted to within 1.10 months (and 75 per cent of the predictions accurate within a four-month range).
It can be argued that it is remarkable that notice periods can be predicted with this level of accuracy and precision using only duration of employment and a simple linear or polynomial formula.[50] This analysis confirms a common intuition that has been acknowledged by most employment lawyers, namely the importance of employment duration in the calculation of notice period, and establishes this observation on the largest possible dataset. This has also been acknowledged by most studies on the Bardal factors.[51] While this conclusion is not surprising, it is very much inconsistent with the Bardal principle, according to which “[t]here can be no catalogue laid down as to what is reasonable notice in particular classes of cases.”[52] However, this direct mathematical correlation between employment duration and notice outcome calls into question the reasoning behind the fact that appellate courts have rejected the rule of thumb approach,[53] namely one month of notice for each year of employment.[54] The rule of thumb approach does in fact seem to be applied by judges.
Judges and commentators have justified the dominance of length of service on several grounds: re-employability/cushion rationale, the inherent worth of a senior employee, and rewarding the loyalty of an employee, among others.[55] Although the predictive power of duration offers the advantage of making notice fairly predictable, excessive reliance on this factor creates discriminatory or undesirable consequences. As argued by Barry Fisher, the sanctity of seniority is based on the false assumption that everyone has the same opportunity to put in the same period of time with one employer. It ignores the fact that some groups, by their very nature, do not have that opportunity (e.g., older immigrants, people with disabilities, and people that have had to relocate).[56] Furthermore, it can be argued that reliance on seniority is problematic if not aligned with the spirit of Bardal, which favours a global assessment. Finally, while Bardal features are strongly correlated, especially age and duration, it may be argued that the simplicity of the duration factor has encouraged judges to undervalue the other factors, as they are more difficult to compute into the final outcome. One possible solution to address this issue would be to develop a strict calculation roadmap for judges and employers with a precise assigned weight for each factor. This would help to integrate the other factors more consistently into the calculation.
C. Beyond Employment Duration: Adjustments According to Other Bardal Factors
While it can be argued that reasonable notice is, to a certain extent, predictable just by taking duration into account, questions have preoccupied lawyers since the Bardal case: How do other variables influence judges’ determinations of notice? Do judges apply the rule of thumb and adjust downward or upward based on other variables? If so, is there a consistent system of adjustment, and how is each variable weighted?
Here is a simplified example: let’s say an employee worked for ten years. According to the rule of thumb, she should be getting between eight- and eleven-months’ notice. The crucial question is whether a judge will choose eight or eleven months and based on what attribute or attributes. A few hypotheses may be envisioned.
First, if there is a consistent judicial system of adjustment, is our model capable of identifying a pattern from the data and quantifying the way judges make the adjustments—that is, expressing how each attribute is reflected in the fluctuations? Previous studies have reported several models of adjustment. In particular, Hart reported the presence of a soft cap limiting the notice period to twenty-four months for managerial employees and to twelve months for non-qualified employees.[57] Thornicroft reported that employees older than fifty get three additional months of adjustment.[58]
Next, perhaps there are a variety of rationales in adjustments of notice periods based on different precedents. For example, in similar cases, a judge might calculate notice based on two separate models of calculation. In this case, the question is whether we can identify clusters with various trends of calculation.
Finally, it is possible that the case law is inconsistent or highly dependent on particular situations, such that no algorithm can predict notice accurately, as the case law does not follow a consistent pattern depending on Bardal factors alone. Considering that our model learns from past cases, if judges are not weighing other attributes in a consistent way, it is not possible to predict any downward or upward adjustment, and little to no correlation will be found with these attributes.
In order to shed some light on these questions, especially concerning how judges make the adjustment calculation described above, we use three methods. First, we integrate multiple features into our algorithm and predict the notice period based on all Bardal features to identify these adjustments. Specifically, we investigate the correlation between the other features and the adjustment, that is, whether factors other than employment duration exert any influence on notice outcome. Second, we test the findings reported in previous empirical studies—for instance, how non-duration features influence judges (e.g., existence of a soft cap)—to determine if our dataset reflects similar phenomena. If we find that these correlations do in fact exist, we call for corrections to the AI models and integrate new norms of adjustment to improve the predictive power of our model. Finally, we investigate how machine learning can help to determine the level of inconsistency in our dataset and determine whether inconsistency signals arbitrariness in judicial decision-making.
1. Prediction Error and Adjustments with Additional Factors
As discussed in Part I, Bardal factors are highly correlated. These correlations highlight an intrinsic difficulty in applying Bardal factors in a principled manner insofar as most features show high levels of correlation among themselves: for instance, employment duration correlates with experience (45 per cent correlation) and age (40 per cent), and age correlates with experience (50 per cent). It does not seem likely that all Bardal factors have independent, cumulative impacts on the notice period; rather, more complex interdependencies appear, making it difficult to draw conclusions in the absence of a statistical model. Some of the features can, however, be discarded as being very weakly correlated to the notice period. For example, we found no significant correlation between notice period and employee gender, or between outcome and province.[59] That said, we noted earlier that the data is largely male-dominant (Figure 1). There may be an unobserved gender effect, such as the fact that women were underrepresented in the labour market until recently, or that women may be less likely to pursue litigation and more inclined to accept comparatively low notice offers.[60]
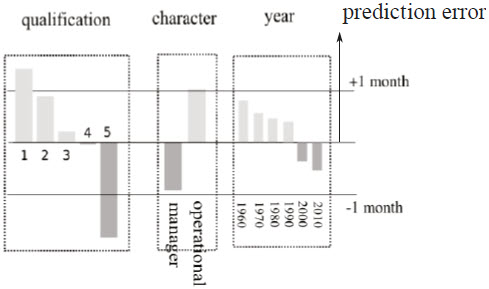
In order to identify the features (other than employment duration) that exert influence on the notice period calculation, we computed the correlation between the adjustment (i.e., the prediction error) and all factors (see Figure 6A, below). We found that all correlations dropped significantly, indicating that employment duration was indeed responsible for a large part of the correlation with other Bardal factors. In particular, we observe that the correlation between the prediction error and experience or age is relatively low (-14 per cent and -17 per cent), in contrast with the high correlations of 54 per cent or 41 per cent found with the notice period itself. This correlation indicates that age and experience do not exert a direct influence on the determination of the notice period, but rather an influence through their correlation with duration of employment, mainly because employees who have worked longer tend to be older and more experienced.
However, a residual correlation remained with the employment qualification (25 per cent correlation) and with the character of employment (22 per cent correlation), two relatively correlated factors. We observed that for employees with the lowest qualifications, the algorithm overestimated the notice period by 2.4 months on average, while for highly qualified employees it underestimated the notice period by 1.45 months on average (Figure 6B, below). Similarly, the algorithm underestimated the notice period of managerial workers by about 0.75 months and overestimated the notice period for operational workers by 0.9 months. These results show that notice periods are longer for more qualified individuals or managers.
Finally, Figure 6B shows a clear negative trend, indicating the evolution of the case law and suggesting that the case law has progressively evolved towards providing more generous notice periods. While strong averaged effects are clearly visible in the graphs of Figure 6, they are subject to important fluctuations, so that it is unclear how taking these adjustments into account will improve the accuracy of the prediction.
Figure 6
Prediction error as a function of variables other than duration of employment
A
Pearson’s correlation
B
Prediction error
Prediction error shows a clear decay, in average, as a function of qualification: notice periods are longer for more qualified individuals. Similarly, longer notice periods were awarded to managers. Eventually, notice periods also became increasingly generous over the years (plot showing average prediction error per decade, starting in 1960).
2. Refining the Prediction: Cumulative Role of Other Bardal Factors
While employment duration shows the highest correlation with notice period, other attributes can also significantly influence judges’ decisions. We systematically investigated how other relevant attributes impact the decision process.
a. Character of Employment
The “character of employment” Bardal factor relates to the dismissed employee’s status, rank, or position in the organizational hierarchy, and relates to “level of employment.”[61] Judges have considered an employee with a higher level of employment to be deserving of a longer notice period for various reasons, including the necessity of providing greater employment-contract protections to make up for the smaller number of job openings for higher-ranking employees to find a comparable position.[62] This was reportedly associated with a soft cap on reasonable notice, limiting notice periods for non-managerial employees to twelve months and for managerial employees to twenty-four months.
In recent years, this classification has been challenged by the courts. Appellate courts have requested evidence to establish the impact of character of employment on the availability of work for the terminated employee. Thus, as argued in the Di Tomaso decision,[63] “character of employment” is of declining importance in assessing reasonable notice. Judges no longer point to an assumption that clerical employees will automatically get new jobs more quickly as a justification for awarding shorter reasonable notice periods.
Recent studies, however, suggest that employees who have elevated status in an organizational hierarchy do receive lengthier reasonable notice awards, controlling for other factors. For instance, Thornicroft’s study of Canadian appellate cases decided between 2000 and 2011 suggests that middle managers were awarded approximately 2.5 months more notice than clerical workers, and senior managers were awarded slightly more than low-middle managers.[64]
Accordingly, we have noted[65] a relatively strong negative correlation between notice period and character of employment (-25 per cent), which, according to our conventions, indicates that operational positions led to shorter notice periods than managerial positions. To assess how this factor contributes to adjusting the notice period, we used a regression algorithm combining both the duration and character of employment.[66] Our regression algorithm was able to distinguish between the managers and operational workers and estimated an average 1.81 additional months of notice in favour of managers. Interestingly, despite this clear statistical impact, the reduction of the error of prediction when taking into account both duration and character of employment is modest, essentially due to the fluctuations associated with these criteria—that is, inconsistent application of these features by judges. Specifically, regression with duration and character of employment reduced the median error to 2.1 months (versus 2.25 for regression with duration only), with 25 per cent of predictions accurate to within 0.9 months and 75 per cent of predictions accurate to within 3.81 months (versus four months for regression with duration only).
Figure 7
Polynomial regression of the data taking into account duration and character of employment (left) and scatter plot of notice periods for managers and operational workers (right).
This suggests that the character of employment does have a cumulative impact on notice period determination, corresponding to an additional 1.81 months’ notice for managers, thereby partly confirming Thornicroft’s results.
We next investigated whether we found empirical evidence supporting the idea that long-term non-managerial employees routinely obtain less than twelve months’ notice (Thornicroft’s soft cap). In fact, Figure 7 shows that 29 per cent of non-managers (181 total cases) obtained more than twelve months and 40 per cent of managers (109 total cases) obtained more than twelve months. For longer employment duration (e.g., greater than eight years), the regression algorithm predicts notice periods longer than twelve months for operational workers.[67] So while there are indeed fewer non-managers obtaining more than twelve months’ notice, there is no statistical evidence for the existence of a soft cap.
In conclusion, the character of employment exerts a consistent and measurable influence on notice, not by inducing a soft-cap limit on notice period directly, but by acting as a systematic shift of slightly less than two months between managers and clerical workers. While it is correlated with other variables, especially qualifications,[68] it is sufficiently independent to exert a cumulative effect. It is important to note that character of employment was found to be negatively correlated with qualification and duration of employment. This correlation suggests that managerial positions are on average associated with higher qualifications and longer durations than operational positions. As a result, it can be argued that managerial workers received longer notice periods because of both their management level and duration of employment.
b. Employee Qualification
We proceeded along the same lines to assess the combined role of employment qualification and length of service in the determination of notice period. Taking into account qualification in addition to duration did not significantly improve the median error despite the visual trend observed. The associated figure, which is less informative, is not shown.
c. Age
Case law suggests that older employees deserve longer notice periods[69] because they may struggle with re-employment and sometimes face age-based labour market discrimination.[70] While this argument has found support in the economic literature,[71] considering that many young employees may also struggle to find employment due to lack of experience or labour market discrimination, it is unconvincing to argue that older employees should systematically receive more generous awards. However, the important question for lawyers is: what is the empirical significance of age in the calculation of notice period?
Many studies have argued that judges rely heavily on age in assessing the length of notice, with older employees receiving significantly longer awards.[72] Thornicroft found that, controlling for other factors, each decade of a dismissed employee’s age contributed to an increase of 0.75 months of notice. Thornicroft also found that age begins to have a significant impact on the assessment once an employee reaches age fifty. For instance, employees who were age fifty or older received about 3.1 months more notice than employees under the age of thirty-five.[73]
The influence of age, however, is difficult to evaluate, as this factor is highly correlated to other factors, particularly duration (40 per cent correlation), experience, and employment availability. Our findings suggest that younger workers (below age thirty-five) and older workers (above age sixty-five) generally obtain shorter notice periods than employees between fifty and sixty years of age, while employees aged forty to fifty demonstrate no bias in the prediction, as shown in Figure 8 (below).
Figure 8
Influence of age in the adjustment of notice period.[74] Prediction error for each data point (circles) as a function of age (bar: mean prediction error, arrowed line: standard deviation) (left); regression to a multivariate polynomial as a function of duration and age (right).
On average, the predictor overestimates notice periods of employees younger than thirty-five by 1.4 months and underestimates notice periods of employees aged fifty to sixty by 1.1 months. However, fluctuations around these ages are significant (gray double arrows), such that even correcting for these biases did not noticeably improve the prediction (Figure 8, left). We obtained a median error of 2.18 months (not significantly distinct from the 2.25 months obtained for duration only), with 25 per cent and 75 per cent quantiles at 1.1 and 3.89 months). Therefore, age has only a modest cumulative influence on notice, if any. Although the fact that an employee is older than a certain age (e.g., fifty) may be extremely relevant in some cases, judges do not seem to apply the age variable consistently, yielding ample fluctuations, such that taking age into account does not improve predictability.
d. Year of Judgment and the Evolution of the Case Law
Figure 6 showed a clear trend in the case law of providing longer notice periods in recent years. However, here again the degree of fluctuation around this trend is quite large, making the impact of correcting for the evolution of the case law quite modest. Regression taking into account duration of employment and year of judgment improved accuracy slightly, lowering the median error to 2.19 months (compared to 2.25 for duration only), with 25 per cent of the predictions accurate to within 0.9 months, and 75 per cent of predictions accurate to within 3.88 months).
e. Availability of Similar Employment
Finally, the Bardal case highlighted availability of similar employment, “having regard to the experience, training and qualifications” of the employee.[75] This factor refers to market conditions and in particular the re-employability of the dismissed employee. According to Fisher, judges rarely engage in statistically based analyses of plaintiffs’ labour market prospects. Instead, Fisher argues, judges may rely on intuition and anecdotal analysis when considering this factor, potentially because judges are not equipped to conduct such analyses and gaining access to usable statistical data is too costly.[76]
Empirical findings on the impact of this feature are markedly mixed. While most studies have found a significant effect,[77] others have not been able to identify any effect. In our analysis, negative correlations were found between notice periods decided by judges and employment availability (-21 per cent). This indicates, in line with the principles of the Bardal criteria, that employees who have fewer opportunities for finding similar employment should be granted longer notice periods.[78] This factor is, however, difficult to measure for non-economists. Judges have wrestled to determine how much weight to give market conditions. On the one hand, judges have sometimes awarded longer notice periods during economic downturns.[79] On the other hand, other judges have acknowledged that employers may also be fighting for their survival in poor economic times and thus, judges should take into consideration both the interest of the employer and employee.[80] While some judges have interpreted the latter approach as authority that notice periods should not be extended during economic downturns, most judges have now taken a moderate position that takes into account poor economic conditions at the time of termination without excessive emphasis.[81]
To appreciate whether employment availability played a cumulative role in the determination of notice periods, we again used our polynomial regression algorithm and predicted notice period as a function of employment duration and availability of other employment. Once again, we observed a modest improvement in the prediction score of the same amplitude as when we took into account character of employment or qualification. The error of prediction did not vary significantly—a median error of 2.27—with 25 per cent of predictions accurate to within 0.88 months and 75 per cent of predictions accurate to within four months.
f. All Bardal Factors Combined for Prediction
Since all variables do seem to provide some improvement to the prediction, we combined all the features to predict the notice period through a regression on a multivariate polynomial model. The model fit the data with an error on the validation set of 2.05 months, with 25 per cent of the predictions accurate to within 0.86 months and 75 per cent of predictions accurate to within 3.59 months. As we will discuss later, limitations in the predictive power of our algorithm can be explained by the approximate and inconsistent application of the Bardal factors, or by the importance of factors independent of the Bardal criteria in the judge’s decision. However, another explanation could be a bias towards round notice periods of six, twelve, or twenty-four months, as noted in the dataset. To correct for this bias, we modified the prediction by rounding to six, twelve, or twenty-four months any prediction falling within six weeks of these durations. This reduced the median prediction error to exactly two months, with 25 per cent of predictions accurate to within 0.76 months (approximately three weeks) and 75 per cent of predictions accurate to within 3.6 months (see Figure 9, below).
Figure 9
Top: Regression with employment duration, character of employment, qualification, employment availability, employee age, and year of judgment (left), together with the rounded prediction (right). Bottom: Error analysis with median and 25–75 per cent quantiles.
Taken together, our analysis shows that while character and duration of employment are both consistent and measurable predictors, the high degree of correlation among all the Bardal factors makes it difficult to assess the weight of each factor on judges’ decisions. While this is encouraging for the application of predictive analytics to notice calculation, it may suggest that a consistent and principled application of Bardal is a complex task for judges insofar as no single Bardal factor operates in a vacuum or exerts any kind of cumulative influence, and the level of error in prediction remains sizable.
In order to further explore the notice determination process and whether other algorithms can reduce the prediction error, we investigated the application of more complex AI methods to notice determination cases and undertook the process of including non-Bardal factors (including legally irrelevant factors) to predict the notice period.
3. The Failure of More Advanced Machine-Learning Algorithms to Reduce the Prediction Error
One possible avenue we explored to improve the capability of our algorithms to predict outcomes is the use of AI algorithms that were more sophisticated than multivariate regressions. The rationale is that regression algorithms may miss possible complex higher-order correlations between the data, even when considering regressions with polynomials. To test this hypothesis, we used two popular methods for machine learning: decision trees (and random forests that combine multiple decision trees) and neural networks. We trained these algorithms on the data and compared the error with regression algorithms. In contrast with the previous part, in which features were added one by one to assess the specific role of each, we ran these methods on the full dataset.
a. Decision Trees and Random Forests
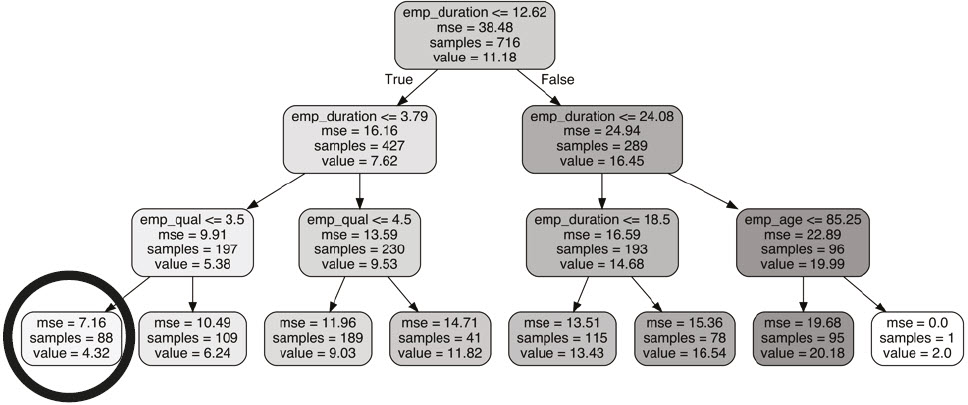
We began by considering the predictions obtained using decision trees. These techniques evaluate the notice period following a flowchart of explicit “if then else” rules, applied sequentially and depending on the values of one attribute at a time. We used the classical “greedy” algorithm to obtain decision trees. These trees are based on iteratively identifying the best rules for reducing the error[82] and the trees finish on so-called leaves that provide the prediction sought. There are thus as many outcomes as there are leaves, which intrinsically limits the precision of these algorithms for regression. An example[83] of such a decision tree is depicted in Figure 10 (below). Predicting notice period given this tree simply consists of following the flowchart from the root (top of the tree, first split) down to the leaves (result predicted). In this particular example, we observe that the decision tree first filters cases according to whether employment duration was fewer than twelve months. If it is (“True”), the left path must be followed. If not (“False”), the right path must be followed. For example, a worker who worked for one year and has low qualification (e.g., employment qualification 1) would follow the right branch from the root (duration fewer than twelve years) and the second node (duration fewer than 3.79 years), as well as for the third node (qualification less than 3.5), giving us our prediction, which corresponds to the final leaf of the tree: the notice period would be 4.32 months.
Figure 10
The best score obtained on the Bardal database with decision trees of depth five yielded an average error of 1.89 months, with 25 per cent of cases accurately predicted to within 0.88 months and 75 per cent of cases accurately predicted to within 3.90 months.
While decision trees are generally very efficient and provide an interpretable model, they have a tendency to overfit the data—that is, they typically reproduce the training data very closely, and therefore lack the capability to generalize to cases not presented in the training dataset. One avenue to achieve better results is to combine multiple decision trees. This technique, called “random forest” algorithms, combines several trees with different source sets and features and makes a prediction according to the outcome of each tree. The algorithm we used, called a “random forest regressor,” constructs a prescribed number of trees, each of which is built based on a random selection of a subset of cases and a random selection of features. It then provides a prediction corresponding to the average prediction across all the decision trees. This randomness generally helps to reduce the variance of the model, in turn providing better predictions. However, the random forest algorithm did not improve the prediction of decision trees. The median error found for a forest with 1,000 estimators, a minimal number of splits and leaves per tree both set to ten, and a maximal depth set to five yielded 1.93 median months, with 25 per cent of cases predicted accurately to within 0.92 months and 75 per cent of predictions predicted accurately to within 3.55 months.
b. Neural Networks
We also turned our attention to more complex and modern machine-learning algorithms that could nominally increase the accuracy and precision of notice predictions. However, this dataset is not well suited for such methods, because of the relatively limited number of available cases.[84] Neural networks with various architectures all overfitted the training set and yielded errors generally above five months for the best algorithm. The best parameters were three layers of sizes ten, twelve, and two, with an activation function ReLU6, 100,000 epochs, implemented using PyTorch[85]; they yielded an average error of 5.9 months on the test set.
Table 1
Comparison of accuracy for the different algorithms (summary of the efficiency of all algorithms used for comparison). The two best algorithms (regression on all parameters and random forests) are italicized. The level of fluctuations, estimated in Part I.C (Figure 2), is in bold.
III. Error Analysis: Machine Learning and Inconsistency in the Calculation of Notice
Given the significant successes of AI in various domains, the relatively poor efficacy found in predicting notice periods may come as a surprise. In order to discover the main obstacles preventing algorithms from providing efficient predictions, we analyzed in depth those cases that were poorly predicted by the algorithms with the aim of identifying potential additional criteria used by judges that were not identified by algorithms. Indeed, one important determiner of the quality of a judicial system is the degree of consistency in judicial decision-making. The problem of inconsistency in legal and administrative decision-making is a cause for concern; it has been argued to be a widespread issue and is well documented in various areas of law.[86] Inconsistency or unreliability of decision-making could be a source of the poor accuracy of predictions. This part investigates cases that were not well handled by machine-learning algorithms as a way to identify possible disparities in reasonable notice cases. This is not an attempt to undertake an exhaustive assessment of these disparities or inconsistencies in this domain of law, a topic that would deserve its own paper. However, it is worth exploring evidence of inconsistency in the Bardal dataset and especially whether these disparities constitute a sign of arbitrariness in decision-making. This part will explore whether machine learning, with the integration of legal data, can offer a mechanism to detect such inconsistencies.
Before we proceed, let us emphasize that a level of consistency in case law is a prerequisite for legal certainty, a central component of the concept of the rule of law. The principle of legal certainty is an essential aspect of many legal systems[87] insofar as it contributes to public confidence in the courts. Conflicting court decisions, especially those of appellate courts, can trigger breaches of the due process requirement. As observed by the European Court of Human Rights, justice must not “degenerate into a lottery.”[88] We argued earlier that machine learning can be used to generate predictions of case decisions based on similarities with previous cases. As such, machine learning can be used as a way to identify inconsistencies in past decisions or used in the future to help decision-makers make better and more consistent decisions. In particular, machine-learning algorithms can help to identify inconsistencies in case law resulting from legally irrelevant factors.[89] Daniel Chen has argued that low predictive accuracy may signal cases of judicial “indifference”—essentially conditions in which judges are unmoved by legally relevant circumstances. For instance, it is possible that circumstances such as the outcome of a football game[90] or the time of day[91] can substantially affect legal decisions.
To address this question, we isolated outliers, defined as the cases in which the predicted notice period (based on precedential trends and restricted to the consideration of a few legally relevant attributes) deviated significantly from the actual decision of the judge. We extracted all cases in which the prediction deviated by four or more months from the actual judge’s decision. This led us to isolate 123 outliers, or 8 per cent of cases (see Figure 11, below). For instance, the outlier labeled “1” in Figure 11 corresponds to Johnson v. James Western Star Ltd., in which it appears that a surprisingly long notice period of twenty-four months was awarded after the plaintiff worked for four years as a salesman (operational work) at a transportation and warehousing company.[92] We investigated the grounds for the judge’s decision (which was confirmed on appeal), and found that the judgement took into account the fact that the worker was induced to leave a senior position with a company he had worked at for twenty-one years and accepted a non-senior role in the company with the promise that he would be promoted; however, employment was terminated before any promotion materialized. The judge concluded that the plaintiff would not have left his job if not for that promise. The notice period was thus determined according to what the judge considered to be a fair outcome and the Bardal factors played a limited role in the calculation of the award. It is not surprising that this case was poorly predicted by the algorithm, since it was not trained to take this variable into consideration. In legal terms, this is a classic case of inducement; the algorithm, not trained to identify inducements, recognized this case as an outlier in that it deviated from the Bardal system.[93]
Similarly, the second outlier in Figure 11 (labelled “2”), Galant v Shomrai Hadath, corresponded to an eighty-eight-year-old employee who had worked for thirty years as a ritual slaughterer with a religious organization. He had strong experience, a high qualification level, and poor employment opportunities.[94] Nominally, these characteristics would lead the algorithm (or the judge) to predict a long notice period; yet the judge awarded a two-month notice period. The judge duly justified this short notice period in the judgment: the owner and sole proprietor of the company was a volunteer for a religious organization and the worker had expressed his intent to retire soon. As we can see, these outliers do not appear to be instances of inconsistent application of law, but rely rather on the particular circumstances of each case.
Figure 11
Outliers (double circles) selected: cases predicted with greater than four-month errors by the optimal algorithm (polynomial regression with all Bardal criteria represented by single circles). Cases 1 and 2 are discussed in the text.
Notwithstanding these unexpected outcomes, they do not constitute instances of inconsistent application of the law. It is clear that special situations such as these cannot be accurately predicted by algorithms based on standardized factual elements and seem essentially impossible to predict by any algorithm. It would be interesting to assess whether this variability lends itself to a small number of prescribed aspects of the cases. In order to identify those elements, we systematically analyzed the 123 outliers. This analysis did not lead us to identify evidence of a disconcerting level of inconsistency that could make Bardal a “jackpot justice” system.[95] In all cases, judges explain at length the exceptional circumstances under which employees are awarded abnormal notice periods in all the outliers extracted. This makes clear that judges share similar standards. For instance, unusually generous awards may be justified by exceptional and aggravating circumstances: relocation, or the fact that the employee was induced to quit their job. Another explanation is that a group of judges have decided to take a different approach on Bardal.
Although this has not been openly discussed in the judgments, it may be argued that some of the judges are pushing for a case law development that is contrary to Bardal. It should be noted that this is not in and of itself contrary to the proper administration of justice. In fact, many judges and scholars have argued that Bardal is a sub-optimal system of calculation to begin with and should be reformed.[96] An example of this evolution of the law is the fact that several of the outlier cases were associated with awards of unusually long notice when the employer acted in bad faith in the manner of dismissal.
In particular, we noticed several outliers related to the Wallace decision[97] regarding the determination of damages arising from claims concerning wrongful dismissal. According to Wallace, a breach of good faith and fair dealing in the manner of termination was compensated through an extension of the common law reasonable notice period. This extension was commonly referred to as “Wallace damages” or “bad faith damages.”[98] In the years following Wallace, we found evidence of several extended notice periods associated with the application of Wallace.[99] When such extensions were awarded, they tended to be in the range of one to four months added to the notice period. However, the limited number of cases calling upon both Bardal and Wallace makes it difficult to achieve statistical significance or to reach any conclusion concerning the way in which these cases were applied. That said, the emergence of new principles such as bad faith invoked in Wallace could call for extending the number of features treated by algorithms; but several years’ worth of history and many dozens of cases would be necessary for an algorithm to appropriately learn how to adjust decisions accordingly. Also, it turns out to be impractical given that in 2008 the Honda decision altered the Wallace approach.[100] Bad faith in the manner of dismissal should no longer be the ground for longer notice periods. Instead, the courts must assess whether mental distress was foreseeable when pursuing a moral damage claim.[101]
In conclusion, we found that judges’ discretionary power to apply general rules or precedent to specific facts led to a large degree of fluctuations, yielding poor predictive abilities for machine-learning algorithms. This is an inherent component of the judicial process (in most areas). While general rules, whether imposed through legislation or precedent, are aimed at protecting against “inconsistency and arbitrariness in decision making, ... rules are often poorly suited for [application to] the fact-intensive contexts that make up a large portion of modern adjudication. In contexts where small and varied deviations in fact ... can substantially impact merits, rules [may often] be crude and insensitive to the particulars of the case.”[102]
We are referring here to a perennial question: what explains differential decision-making by judges? Our findings support the claim that while there are statistical relationships between notice period, duration of employment, and other factors related to employment and employee status, there exist unpredictable variations across cases. Due to the consideration of factors that are independent of these factual elements, judges adjust the weight associated with each Bardal factor to substantially alter reasonable notice based on a global assessment of all aspects of the case at hand.
This leads us to another important issue: the question of whether there is too much inconsistency in the determination of notice. Although many scholars have used one-dimensional measures to assess the predictability of reasonable notice,[103] they likely understate the interdependency of the Bardal factors. The notice period system is the home of subtle disparities. By assessing each Bardal feature—such as age or experience—separately, scholars are missing many of the inter-judge disparities in the application of Bardal factors, especially how judges interpret the interdependency of the Bardal features.[104] This is what Copus, Hubert, and Laqueur refer to as heterogeneous treatment effects.[105] For example, two judges may award the same notice period without agreeing that older employees deserve longer notice. Roughly speaking, this means that two decision-makers may make similar decisions, even if they sometimes disagree. The question of possible individual judicial bias will, however, remain very hard to gauge due to the limited number of cases treated by each judge. Future research could investigate groups of judges (e.g., according to judges’ political inclinations, whether pro-labour or pro-management, etc.).
In our opinion, this level of inconsistency is not only tolerable, but also suggests that reasonable notice strikes a good balance between predictability and flexibility. On the one hand, the Bardal system is sufficiently predictable. On the other hand, it is sufficiently flexible to be adapted to the specific circumstances of a case and is mostly driven by legally relevant variables. While legal certainty is essential to the rule of law, a judicial system that is too predictable is not only overly ambitious, it also suggests the existence of a rigid status quo. This may be problematic, especially if the status quo is unfair or if the decision-making is heavily influenced by extraneous factors that seem inequitable. For instance, in the matter of asylum adjudication in the United States, Dunn et al were able to predict the final outcome of a case with 80 per cent accuracy at its outset, using only information on the identity of the judge handling the case and the applicant’s nationality.[106] Work such as this shows that in some areas, “[i]nteresting patterns emerge related to whether judges become harsher before lunchtime or toward the end of the day, how family size is associated with grant rates, and how the day’s caseload is associated with grant rates.”[107] As argued earlier, reasonable notice determination did not appear to be affected by such structural bias. Instead, we argue that the fact that machine-learning models are inherently backward-looking, in the sense that they use statistical analysis of past decisions to inform future decisions, tethers future decisions to the status quo. Indeed, this tethering to the past may be problematic if past decisions are or become incompatible with current values. For example, the economic circumstances of the 2010s following the global financial crisis were very different from the current economic context. Using past data to calculate notice may not accurately reflect what a judge would decide today.
Furthermore, while advanced algorithms can help to predict the big picture, it would be surprising if they were able to predict exact awards (e.g., with 90 per cent accuracy with a range of plus or minus two weeks) as long as judges have sufficient flexibility to adapt their decisions to specific facts. It may also be argued that machine-learning algorithms should not aim to predict every aspect of a judicial decision, as this may crystallize the status quo and stall case law development. If the status quo should happen to be unfair, this would be highly problematic. But even if the status quo is fair, changes in society may trigger the need for a new precedent or an adaptation of the law to societal changes. In the case of notice determination, the argument that skilled workers deserve longer notice than unskilled workers does not sit well in a society in which most unskilled jobs are threatened by automation. A society’s code of law is a living organism dependent on realities that are constantly changing. This is what Aharon Barak describes as bridging the gap between law and society.[108]
Conclusion
In this paper, we proposed principled academic analysis of the application of AI methods to notice determination. We developed a variety of statistical models that predicted, with various degrees of accuracy, the notice period decided by the judge based on a few factual criteria related to the case treated. From simple models to modern artificial neural networks, we found that no algorithm was able to achieve average accuracy within two months of actual outcomes when it came to predicting notice periods. We thus explored in more detail the origin of these poor predictions. We suggest that an important part of the prediction error is due to the intrinsic complexity of judicial decision-making, the necessary flexibility applied by the judges to produce fair decisions appropriate to each single case, and the evolution of the principles of the law. Another conclusion drawn from our study is that the high level of interdependency among the Bardal features[109] makes it very difficult to isolate the weight of each factor. For instance, age is strongly correlated with duration and experience: employees with a longer duration of employment are likely older, and thus notice is likely longer. While the other features besides duration undoubtedly exert a significant influence on judge’s decisions, our algorithm has not allowed us to decisively determine the influence pattern of each feature. One reason is that judges do not take these features into account consistently.
This conclusion has been echoed by the Ontario Court of Appeal, which has described the process of determining reasonable notice as “an art not a science.”[110] In fact, it can be argued that while notice may be sufficiently predictable, “there is no one ‘right’ figure.”[111] Judges are supposed to consider the Bardal factors and then decide “what appears to be logical, judicious, fair, equitable, sensible, and not excessive,”[112] according to the judge in question. It seems that judges are first considering duration and then making a global assessment on a case-by-case basis, with cases yielding no consistent pattern and thus being difficult to compute into a model. In fact, we argue that Bardal is neither art nor science: it lies somewhere in between. Some aspects of judicial decision-making are certainly scientific. For instance, judges seem to be very consistent when it comes to the duration factor insofar as there is a linear relationship between duration and notice. However, judges weigh a variety of other features in making a decision; for an algorithm trained on past decisions and relying on a few factual elements, this adjustment remains fully unpredictable, and may remain essentially unpredictable, in that it may depend on individual judges’ sensitivity to the specific circumstances of certain cases.
To progress in this direction, we undertook the collection and analysis of a more extensive dataset, including factual elements not traditionally considered, in collaboration with a team of data scientists at McGill University’s Desautels Faculty of Management. The analysis of these datasets is beyond the scope of the present study, yet some encouraging preliminary observations tend to show that industry sector, unemployment rates in the province where cases are treated (rising in Alberta and New Brunswick, compared to the strong economies of Ontario and British Columbia), or hourly compensation levels (potentially reflecting the employee’s status or market pressure) seem to reflect some correlation with notice periods.
From an academic viewpoint, this study outlines a general scientific methodology that could serve as a basis for studies using AI to predict outcomes of trials in other areas of law and in other legal systems that are facing similar issues. From an AI research perspective, we expect this project to open a new frontier in cause-effect relationships and counterfactual reasoning, a core problem in the field of AI. This project will be especially significant if we succeed in developing learning models that are sufficiently advanced to understand judicial texts and reasoning. Ultimately, our future research will involve the application of deep-learning techniques to large legal and negotiation texts. We hope that it may contribute to the development of semantic representations of reasoning, notably because causality and counterfactual reasoning are critical components of legal and negotiation language data.
From a practical viewpoint, the algorithms we developed and the predictions they provide open the way to the development of access to justice for all. In fact, this research is part of a longer-term project aimed at facilitating access to legal help for self-represented litigants, who often do not have access to sufficient legal help and who constitute the majority of litigants in the United States and Canada. For instance, people who have been terminated by their employers may be offered less than what they are entitled to, but under the current system, most employees have no way of knowing whether that is true or how much they should claim. It can be argued that the average litigant should receive at least enough legal support to be able to evaluate whether he or she is being treated fairly. This research also has applications in industry areas such as customer dispute resolution analytics for large firms. In fact, we believe that future research may focus on predictive negotiation models, a crucial aspect of small-claims dispute resolution (including, but not limited to, employment), insofar as most small-claims disputes are resolved through negotiation. In the longer term, this pilot project could be scaled up by deploying the platform within the court systems of provincial governments as well as within judicial systems outside Canada. We believe that if the AI-powered legal aid system is integrated into the court system, it will carry more authority, giving the parties greater confidence in both the process and the outcome.
Parties annexes
Appendix
Addendum
A1. Conventions and Features Included in the Database (Features in Italics)
-
Case ID (unique label for each case in the database)
-
Name of the research assistant who analyzed and annotated the case
-
Case reference (litigants’ names)
-
Year of the case
-
Type of employment (Permanent / Temporary / Contractor / Seasonal)
-
Employment duration (in years; duration does not have to be an integer number)
-
Age of employee (in years, with the convention that imprecise information such as “early 40s,” “mid 40s,” or “late 40s” were replaced with 42.5, 45, and 47.5 years old)
-
Availability of similar employment (on a 1–5 scale)
-
1 - Very tight market and exposed to automation (risk of displacement—e.g., cashier)
-
2 - Little availability, but not exposed to displacement (e.g., worker has to move to find another job)
-
3 - Executive positions or highly specialized job (difficult to obtain)
-
4 - Competitive, but jobs available (typically, entry- to mid-level positions for qualified workers)
-
5 - Non-specialized job in high demand (e.g., waiters, vocational jobs) or very specialized jobs in high demand (e.g., engineering)
-
-
Job title
-
Character of employment
-
1 - Managerial (senior, high-level, or management employee; skilled or technically demanding position)
-
2 - Operational (junior, semi-skilled, or non-managerial employee)
-
-
Experience of the employee (on 1–5 scale)
-
1 - 0–5 years in the field
-
2 - 6–10 years in the field
-
3 - 11–15 years in the field
-
4 - 16–20 years in the field
-
5 - 21+ years in the field
-
-
Industry (SIC number)
-
Employee qualifications (including training; on a 0–5 scale)
-
0 - No qualifications
-
1 - Low qualifications or qualifications unrelated to the position
-
2 - Decent qualifications, but in another field
-
3 - Decent qualifications in the position
-
4 - Good qualifications for the position
-
5 - Top qualifications for the position
-
-
Institution judging the case (e.g., SCC, British Columbia Supreme Court, etc.)
-
Judge name
-
Employee gender
-
Outcome (notice period in months)
-
Comments (e.g., any specific argument used by the judge to support the decision)
A2. Example of Termination Compensation Calculator on MyOpenCourt.org
Notes
-
[1]
See Maxime C Cohen, Samuel Dahan & Colin Rule, “Conflict Analytics: When Data Science Meets Dispute Resolution”, Management Bus Rev [forthcoming in 2021]; Mark K Osbeck, “Using Data Analytics Tools to Supplement Traditional Research and Analysis in Forecasting Case Outcomes” (2015) 20 Leg Writing 33.
-
[2]
See Owen Byrd, “Moneyball Legal Analytics Now Online for Commercial Litigators” (2017) 31:2 Commercial L World 12; Jennifer Dixon, “Review of Legal Analytics Platform”, LitigationWorld (23 September 2016), online (pdf): <lexmachina.com> [perma.cc/9C3J-936R] (describing the cost of predictive analytics platforms for patent cases).
-
[3]
See Roger Guimerà & Marta Sales-Pardo, “Justice Blocks and Predictability of U.S. Supreme Court Votes” (2011) 6:11 PLOS One 1, online: <journals.plos.org> [perma.cc/NM83-G5DJ].
-
[4]
See Lucianna Ciccocioppo, “There Is No Justice Without Access to Justice: Chief Justice Beverley McLachlin” (11 November 2011), online: University of Toronto Faculty of Law <www.law.utoronto.ca> [perma.cc/EBM2-KY8S].
-
[5]
Roger Fisher and William Ury introduced the idea of a BATNA as one’s best alternative to a negotiated agreement. The reason you negotiate with someone is to produce better results than would otherwise occur. If you are unaware of what results you could obtain if the negotiations are unsuccessful, you run the risk of entering into an agreement that you would be better off rejecting, or rejecting an agreement you would be better off entering into. See Getting to Yes: Negotiating Agreement Without Giving In (Boston: Houghton Mifflin, 1981).
-
[6]
See Harry Surden, “The Ethics of AI in Law: Basic Questions” in Markus D Dubber, Frank Pasquale & Sunit Das, eds, The Oxford Handbook of Ethics of AI (New York: Oxford University Press, 2020) 719.
-
[7]
See Angela Chen, “How Artificial Intelligence Can Help Us Make Judges Less Biased” (17 January 2019), online: The Verge <www.theverge.com> [perma.cc/7Q9R-ZL67].
-
[8]
In fact, many legal technology companies claim to achieve predictions with remarkably high accuracy. Lex Machina, ROSS Intelligence, and Blue J Legal claim to achieve prediction with 90 per cent accuracy. See e.g. “Blue J L&E Accurately Predicts Reasonable Notice” (1 December 2017), online (blog): Blue J Legal <www.bluejlegal.com> [perma.cc/K9EM-8B2H].
-
[9]
See Steven L McShane, “Reasonable Notice Criteria in Common Law Wrongful Dismissal Cases” (1983) 38:3 RI 618; Terry H Wagar & Kathy A Jourdain, “The Determination of Reasonable Notice in Canadian Wrongful Dismissal Cases” (1992) 43:1 Lab LJ 58.
-
[10]
See Bardal v Globe & Mail Ltd, [1960] 24 DLR (2d) 140, OWN 235 (Ont H Ct J) [Bardal cited to DLR]. While 1,500 cases may not seem like a significant amount of data from a classic data science point of view, it is actually a significant dataset for a specific legal question such as notice determination.
-
[11]
The Conflict Analytics Lab launched an open-access technology platform—MyOpenCourt.org—in June 2020 to help workers and small- to medium-sized companies. It uses AI to determine the odds of winning a case in the field of employment law, including calculating severance, overtime, and determining whether a worker is an independent contractor or an employer. Should the algorithm conclude that the user has a case, we give them the option of talking to a lawyer at no cost to them.
-
[12]
A team that includes Yuri Levin, Director of the Scotiabank Centre for Customer Analytics and Professor at Queen’s Smith Business School; Mikhail Nediak, Professor at Queen’s Smith Business School; Stephen Thomas, Professor at Queen’s Smith Business School; Farhana Zulkernine, Professor at Queen’s School of Computing; and Xiaodan Zhu, Professor in Queen’s Electrical Engineering Department.
-
[13]
These students are Imad Ghani, Arnoosh Golestanian, and Neal Gilmore.
-
[14]
Shane Liquornik, Simon Townsend, Brandon Loehle, Max Saunders, David Liang, Will Quaglietta, Mackenzie Anderson, and Zach Berg.
-
[15]
See “Termination Compensation Calculator” output example in Addendum A2, below. This is an open-access platform for the determination of reasonable notice periods. Project partly funded by the New Frontier Grant and the Scotiabank Centre for Customer Analytics.
-
[16]
Furthermore, while data science and machine learning have already produced significant results in many fields, to our knowledge, the possible benefits of their application to dispute resolution have not yet been fully explored.
-
[17]
See “Employment Termination Calculator” output example in Addendum A2, below.
-
[18]
See Jonathan Benchimol, Sophia Kazinnik & Yossi Saadon, “Text Mining Methodologies with R: An Application to Central Bank Texts” (2020) Bank of Israel Research Department Occasional Paper 2020.01 at 43, online (pdf): <www.boi.org> [perma.cc/9UWC-CQ5Q]; Mehdi Allahyari et al, “A Brief Survey of Text Mining: Classification, Clustering and Extraction Techniques” (2017), online (pdf): arXiv <arxiv.org> [perma.cc/9MUV-NNCE]; Julia Silge & David Robinson, Text Mining with R: A Tidy Approach (Sebastopol, Cal: O’Reilly Media, 2017).
-
[19]
The Queen’s Scotiabank Centre for Customer Analytics and Queen’s School of Computing have provided further resources towards the development of supervised text-analytics models and predictive negotiation models.
-
[20]
See supra note 10.
-
[21]
There is no obligation to provide reasonable notice when there is a lawful termination provision or where there is a fixed-term contract. See Machtinger v HOJ Industries Ltd, [1992] 1 SCR 986, 91 DLR (4th) 491 [Machtinger cited to SCR]. See also Bruce Curran & Sara Slinn, “Just Notice Reform: Enhanced Statutory Termination Provisions for the 99%” (2017) 20 CLELJ 229 at 230–31; David J Doorey, The Law of Work: Common Law and the Regulation of Work (Toronto: Emond, 2016) ch 13 [Doorey, The Law of Work]; The Labour Law Casebook Group, Labour and Employment Law: Cases, Materials, and Commentary, 9th ed (Toronto: Irwin Law, 2019) at 297–311.
-
[22]
Most employment contracts are of indefinite length, and the law implies a term that employers must provide employees with reasonable notice that the relationship is ending. See e.g. Machtinger, supra note 21 at 997.
-
[23]
Bardal, supra note 10 at 145 [emphasis added].
-
[24]
For a list of features and scales used, see Addendum A1, below.
-
[25]
We are exquisitely aware that training our AI system with potentially biased decisions could result in biased and discriminatory predictions that would perpetuate the status quo. For instance, if in past cases a specific category of employees tended to get lower notice packages, our system (trained with these cases) could predict a shorter notice for that category of platform users, possibly influencing their decisions about how to proceed. Accordingly, in order to avoid discrimination, we have trained two versions of the system: one using datasets containing information on the gender and race of the parties, and one with that data removed such that the outcomes are based strictly on factors relevant to the case. Thus, we systematically looked for possible biases in the decisions.
-
[26]
See Addendum A1, below.
-
[27]
Standard deviation quantifies the typical amplitude of the fluctuations of data around the mean and measures the dispersion of the data.
-
[28]
The median of a distribution corresponds to the value M such that there are as many cases above M as there are below M. This measures the centre of a distribution, or typical value, for data sets that are not necessarily symmetrical around their average, as in the case of work duration, which has a decreasing histogram. Typical fluctuations around the median are quantified using the median absolute deviation (MAD, also known as median absolute error), defined as the median of the absolute value of the difference between data points and their median.
-
[29]
See Addendum A1, below.
-
[30]
10 per cent had employment availability 1; 35 per cent scored 2; 29 per cent scored 3; 14 per cent scored 4; and 12 per cent scored 5.
-
[31]
The mode for a statistical dataset is the value occurring most frequently.
-
[32]
These same three graphs are boxed in Figure 3, below.
-
[33]
See Addendum A1, below.
-
[34]
See Addendum A1, below.
-
[35]
Vertical bars indicate median notice period awarded; arrows indicate typical fluctuation. We removed situations in which there were fewer than three cases available, since more cases are necessary to appreciate the fluctuations.
-
[36]
It is worth noting that our model takes into consideration only the Bardal factors and several specific non-Bardal factors. Future research endeavours will explore how advanced neuro-linguistic programming techniques (machine learning and deep learning) may help to improve the predictive power of our models and perhaps identify new predictors.
-
[37]
See Kevin D Ashley, Artificial Intelligence and Legal Analytics: New Tools for Law Practice in the Digital Age (Cambridge, Mass: Cambridge University Press, 2017) ch 4.
-
[38]
At the same time, we computed Pearson’s correlation coefficients across variables to assess how much the different variables are correlated. We obtained similar results on feature importance using alternative algorithms such as the backward elimination method, the recursive elimination method (REM), and the LASSO regularization method. See Trevor Hastie, Robert Tibshirani & Jerome Friedman, The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed (New York: Springer, 2009) chs 3.4, 18.3.4, DOI: <10.1007/978-0-387-84858-7>.
-
[39]
These are real values between -1 and 1. See Karl Pearson, “Note on Regression and Inheritance in the Case of Two Parents” (1895) 58:350 Proceedings Royal Society London 240, DOI: <10.1098/rspl.1895.0041>.
-
[40]
See Addendum A1, below.
-
[41]
See Curran & Slinn, supra note 21 at 238; Kenneth William Thornicroft, “The Assessment of Reasonable Notice by Canadian Appellate Courts from 2000 to 2011” (2013) 17 CLELJ 1 at 26 [Thornicroft, “Assessment of Reasonable Notice”].
-
[42]
See Thornicroft, “Assessment of Reasonable Notice”, supra note 41 at 26–27. According to the “rule of thumb” principle, reasonable notice is based on one month of notice for every year of service. The first case to have adopted this principle was in Ryshpan v Burns Fry Ltd [1995] OJ No 1132 (QL), 10 CCEL (2d) 235. This “rule of thumb” concept was picked up and adopted in Bullen v Protor & Redfern Ltd, [1996] OJ No 340 (QL), 20 CCEL 36 and in McKay v Eaton Yale [1996] 31 OR (3d) 216 at 225–29, 66 ACWS (3d) 1089.
-
[43]
See Kenneth Wm Thornicroft, “Severance Pay and the Older Worker: Negotiated Versus Litigated Outcomes Under Canadian Common Law” (2015) 52:4 Alta L Rev 779 at 793 [Thornicroft, “Severance Pay and the Older Worker”].
-
[44]
See Hastie, Tibshirani & Friedman, supra note 38 at 43–93.
-
[45]
See Fabian Pedregosa et al, “Scikit-Learn: Machine Learning in Python” (2011) 12 J Machine Learning Research 2825.
-
[46]
“[A] rule of thumb that an employee is entitled to one month's notice for every year worked should not be applied. To do so would undermine the flexibility that must be used in determining the appropriate notice period” (Minott v O'Shanter Development Company Ltd (1999), 42 OR (3d) 321 at 323, 168 DLR (4th) 270 (CA) [Minott].
-
[47]
See Part I.B, Figure 2, above.
-
[48]
Notice periods lower than the linear model prediction for short and long periods of service rarely exceeded twenty-four to thirty months.
-
[49]
We optimized both on the degree of the polynomial and the coefficients and found that the optimal degree allowing good predictions and generalization scores (maximizing the cross-validation score) was p=2. Fitting the model to a polynomial of degree two yields α0 = 11.2 months, α1 = 7 months/year and α1 = 7 months/year2 (all having p-values lower than 0.1 per cent and relatively small confidence intervals, thus indicating that the quadratic correction is statistically significant and the coefficient well determined).
-
[50]
The Labour Law Casebook Group, supra note 21 at 297–311.
-
[51]
See Patrick Hart, “Harper v. Lafarge: Summary Judgement and the Assessment of Reasonable Notice in Wrongful Dismissal Cases” (2018) 21:1 CLELJ 189; Thornicroft, “Assessment of Reasonable Notice”, supra note 41 at 26.
-
[52]
Bardal, supra note 10 at 145 [emphasis added].
-
[53]
See Minott, supra note 46 at 323.
-
[54]
Previous research analyzed the “rule of thumb” for employees dismissed within their first three years of employment, and the present result generalizes this approach to the case of employees with longer service. See Thornicroft, “Assessment of Reasonable Notice”, supra note 41 at 26–27. Cf Barry B Fisher, “Revisiting Reasonable Notice Periods in Wrongful Dismissal Cases: 2006 Edition” (2006), online (pdf): Barry Fisher Arbitration & Mediation <barryfisher.ca> [perma.cc/QD54-798C].
-
[55]
See Curran & Slinn, supra note 21 at 237–38.
-
[56]
See Barry B Fisher, “A New & Improved Theory of Reasonable Notice for Wrongful Dismissal After Honda Canada Inc. v. Keays” (12 June 2008) at 7–8, online (pdf): Barry Fisher <barryfisher.ca> [perma.cc/6V4N-K62W] [Fisher, “New & Improved Theory”].
-
[57]
See Hart, supra note 51 at 202. See also Curran & Slinn, supra note 21 at 243.
-
[58]
See Thornicroft, “Assessment of Reasonable Notice”, supra note 41 at 20.
-
[59]
According to previous research, women receive about 1.5 to 1.7 months less notice than comparable male employees. See Kenneth Wm Thornicroft, “Gender Bias in the Negotiation of Severance Pay in Lieu of Reasonable Notice” (2011) 16:2 J Workplace Rights 131 at 141 [Thornicroft, “Gender Bias”].
-
[60]
See Terry H Wagar & James D Grant, “The Relationship Between Plaintiff Gender and Just Cause Determination in Canadian Dismissal Cases” (1996) 34:7/8 Sex Roles 535 at 545–46; James D Grant & Terry H Wagar, “Willingness to Take Legal Action in Wrongful Dismissal Cases: Perceptual Differences Between Men and Women” (1992) 74:3 (supplement) Perceptual & Motor Skills 1073; Thornicroft, “Gender Bias”, supra note 59 at 136.
-
[61]
See The Labour Law Casebook Group, supra note 21 at 297–311; Cronk v Canadian General Insurance Co (1995), 128 DLR (4th) 147 at 156–59, 25 OR (3d) 505 (CA).
-
[62]
See Wilkinson v T Eaton Co (1992), 2 Alta LR (3d) 71 at 83, 130 AR 55 (QB), aff'd (1992), 6 Alta LR (3d) 12, 135 AR 217 (CA); Ellsworth v Murray Canada Inc (1997), 33 CCEL (2d) 253 at paras 40–41, 76 ACWS (3d) 110 (Ont Ct J).
-
[63]
Di Tomaso v Crown Metal Packaging Canada LP, 2011 ONCA 469.
-
[64]
See Thornicroft, “Severance Pay and the Older Worker”, supra note 43.
-
[65]
See Figure 4, above.
-
[66]
See Figure 7, below.
-
[67]
To further assess whether judges tend to adjust down notice periods above twelve months for operational employees, we considered the prediction error provided by the algorithm for such employees when the algorithm predicts more than a year’s notice. The averaged difference between the prediction and the actual outcome for operational workers is 0.21 months when the prediction is above a year and -0.21 months otherwise, which is very similar to the level of error made for managers (-0.35 months versus 0.18 months). Neither represents statistically significant differences from a zero error.
-
[68]
See Figure 4, above.
-
[69]
See e.g. Kotecha v Affinia Canada ULC, 2014 ONCA 411; Orlando v Vancouver Coastal Health Authority, 2005 BCSC 926 at para 49.
-
[70]
See McKinney v University of Guelph, [1990] 3 SCR 229 at 299,76 DLR (4th) 545; Law v Canada (Minister of Employment and Immigration), [1999] 1 SCR 497 at para 101, 170 DLR (4th) 1.
-
[71]
See Statistics Canada, Employment Transitions Among Older Workers Leaving Long-term Jobs: Evidence from Administrative Data, by Aneta Bonikowska & Grant Schellenberg, Catalogue No 11FOO19M–No 355 (Ottawa: Statistics Canada, January 2014).
-
[72]
See Steven L McShane & David C McPhillips, “Predicting Reasonable Notice in Canadian Wrongful Dismissal Cases” (1987) 41:1 Indus & Lab Rel Rev 108 at 113–15; Helen Lam & Kay Devine, “Reasonable Notice for Wrongful Dismissal: Court Versus Human Resource Decisions” (2001) 56:2 RI 365 at 382–88; Thornicroft, “Assessment of Reasonable Notice”, supra note 41 at 16; Thornicroft, “Severance Pay and the Older Worker” supra note 43 at 787–94.
-
[73]
See Thornicroft, “Severance Pay and the Older Worker”, supra note 43 at 795.
-
[74]
The prediction error from the polynomial fit with duration shows a slight averaged overestimation of the notice period for workers younger than thirty-five or older than sixty-five, and a slight underestimation for workers aged fifty to sixty-five, but the fluctuations of the datapoints (circles) are significant (arrowed line: standard deviation), explaining why a regression taking into account duration and age (right) barely improves predictions.
-
[75]
Bardal, supra note 10 at 145.
-
[76]
See Fisher, “New & Improved Theory”, supra note 56 at 9–10.
-
[77]
See McShane & McPhillips, supra note 72 at 113–15.
-
[78]
See The Labour Law Casebook Group, supra note 21 at 297–311.
-
[79]
See Lim v Delrina (Canada) Corp 1995 CanLII 7271 at para 31, 8 CCEL (2d) 219 (Ont Sup Ct).
-
[80]
See Bohemier v Storwal International Inc, [1982] 40 OR (2d) 264, 142 DLR (3d) 8 (Sup Ct).
-
[81]
See Geoffrey England, Individual Employment Law (Toronto: Irwin Law, 2000) at 312–13; Hunter v Northwood Pulp and Timber Ltd, [1985] 62 BCLR 367, 7 CCEL 260 (CA).
-
[82]
Technically, we computed the error (accuracy of prediction) as the coefficient of determination (the R2 score). This score roughly indicates how the fraction of the variance is explained.
-
[83]
See scale for classification of employee qualifications in Addendum A1, below.
-
[84]
To achieve optimal generalization accuracy levels, the training dataset for a neural network needs to be large enough to avoid overfitting: see Martin Anthony & Peter L Barlett, Neural Network Learning: Theoretical Foundations (Cambridge, UK: Cambridge University Press, 2009). A rule of thumb was proposed to have fifty times more data than weights in a neural network: see Ahmad Alwosheel, Sander van Cranenburgh & Casper G Chorus, “Is Your Dataset Big Enough? Sample Size Requirements When Using Artificial Neural Networks for Discrete Choice Analysis” (2018) 28 J Choice Modelling 167. Using this rule of thumb, a dataset of 1,500 inputs would allow for a maximum of thirty weights; with about fifteen features (requiring fifteen input neurons), this limits drastically the possible architectures.
-
[85]
See Adam Paszke et al, “Automatic Differentiation in PyTorch” (Paper delivered at the 31st Conference on Neural Networking Information Processing Systems, Long Beach, CA, 2017) [unpublished].
-
[86]
See Ryan Copus, Ryan Hubert & Hannah Laqueur, “Credible Prediction: Big Data, Machine Learning and the Credibility Revolution” in Michael A Livermore & Daniel N Rockmore, eds, Law as Data: Computation, Text, and the Future of Legal Analysis (Santa Fe: Santa Fe Institute Press, 2019) 21; Kate Stith & José A Cabranes, Fear of Judging: Sentencing Guidelines in the Federal Courts (Chicago: University of Chicago Press, 1998); Jaya Ramji-Nogales, Andrew I Schoenholtz & Philip G Schrag, “Refugee Roulette: Disparities in Asylum Adjudication” (2007) 60 Stan L Rev 295.
-
[87]
The principle of legal certainty is implicit in all the articles of the European Convention on Human Rights and constitutes one of the basic elements of the rule of law: see Beian v Romania (No 1), No 30658/05, [2007] V ECHR 193 at para 39.
-
[88]
Nejdet Şahin and Perihan Şahin v Turkey, No 13279/05, [2011] ECHR 1787 at para 17 (Bratza, Casadevall, Vajić, Spielmann, Rozakis, Kovler & Mijović JJ, dissenting), 54 EHRR 20.
-
[89]
Daniel L Chen, “Machine Learning and the Rule of Law” in Livermore & Rockmore, supra note 86, 433; Copus, Hubert & Laqueur, supra note 86.
-
[90]
See Daniel L Chen & Holger Spamann, “This Morning’s Breakfast, Last Night’s Game: Detecting Extraneous Factors in Judging” (2016) Institute for Advanced Study in Toulouse Working Paper No 16-49.
-
[91]
See Shai Danziger, Jonathan Levav & Liora Avnaim-Pesso, “Extraneous Factors in Judicial Decisions” (2011) 108:17 Proceedings National Academy Sciences 6889.
-
[92]
See Johnson v James Western Star Ltd, 2001 BCSC 1008 at paras 2, 51.
-
[93]
See Doorey, The Law of Work, supra note 21 at 163.
-
[94]
See Galant v Shomrai Hadath, Kashruth Council Orthodox Division, [1996] OJ No 2 (QL) at para 23, 60 ACWS (3d) 306 (Ct J (Gen Div)).
-
[95]
See e.g. Ryan Copus & Ryan Hübert, “Detecting Inconsistency in Governance” (2018) at 3, online (pdf): Social Science Research Network <papers.ssrn.com> [perma.cc/NWN6-8FFD].
-
[96]
See e.g. David Doorey, “Is It Time to Abolish ‘Reasonable Notice’ in Employment Contracts?” (19 November 2013), online (blog): Canadian Law of Work Forum <lawofwork.ca> [perma.cc/Q6FJ-8DHZ].
-
[97]
See Wallace v United Grain Growers Ltd, [1997] 3 SCR 701, 152 DLR (4th) 1 [cited to SCR].
-
[98]
See ibid at paras 73–77, 95, 148.
-
[99]
See e.g. Noseworthy v Riverside Pontiac-Buick Ltd, [1998] 168 DLR (4th) 629, 39 CCEL (2d) 37 (Ont CA); Hughes v Gemini Food Corp, [1997] 97 OAC 147, 27 CCEL (2d) 204 (Ont CA); Pagliaroli v Rite-Pak Produce Co Limited, 2010 ONSC 3729; Antonacci v Great Atlantic & Pacific Company of Canada, Limited, [2000] 181 DLR (4th) 577, 48 CCEL (2d) 294 (Ont CA).
-
[100]
See Honda Canada Inc v Keays, 2008 SCC 39.
-
[101]
See ibid at paras 55–59, 87.
-
[102]
Hannah Laqueur & Ryan Copus, “Synthetic Crowdsourcing: A Machine-Learning Approach to Inconsistency in Adjudication” (2017) at 3, online (pdf): Social Science Research Network <papers.ssrn.com> [perma.cc/RYQ8-K4PH].
-
[103]
See Thornicroft, “Assessment of Reasonable Notice”, supra note 41 at 8–9.
-
[104]
See Figure 4, above.
-
[105]
See Copus, Hubert & Laqueur, supra note 86.
-
[106]
See Matt Dunn et al, “Early Predictability of Asylum Court Decisions,” (2017) at 2–3, online (pdf): Social Science Research Network <papers.ssrn.com> [perma.cc/8TMJ-GSD3].
-
[107]
Ibid at 1. See also Daniel L Chen & Jess Eagel, “Can Machine Learning Help Predict the Outcome of Asylum Adjudications?” (2017) at 1, online (pdf): Social Science Research Network <papers.ssrn.com> [perma.cc/ES8T-N2MP].
-
[108]
Aharon Barak, The Judge in a Democracy (Princeton: Princeton University Press, 2006) at 3–5.
-
[109]
See Figure 4, above.
-
[110]
Minott, supra note 46 at para 62.
-
[111]
Ibid at para 62.
-
[112]
Erskine v Viking Helicopter Ltd, [1990] 35 CCEL 322 at 326, 23 ACWS (3d) 927 (Ont Ct J (Gen Div)).
Liste des figures
Figure 1
Description of the dataset. From left to right: Gender distribution and histograms for duration of employment (in years), notice period (hereafter, outcome) with peaks at 6, 12, 18 and 24 months highlighted, and claimant age (bell-shaped curve centred at 47 years). Idealized smooth profile drawn in black.
Figure 2
Notice period data points for relatively highly qualified operational workers (qualification score 4): as a function of age, all durations together (A); as a function of employment duration, all ages together (B); or for workers aged 40–50 years old (C).[32] Each circle represents one data point (i.e., one decision) and the height of the associated bar is the median notice period. Variations around this averaged decision give a sense of the fluctuation (vertical bar: MAD) of the outcome.[33]
Figure 3
Notice period data points as a function of age, all durations together (top panels), or as a function of employment duration, all ages together (middle) or for workers aged 40–50 years old (bottom), split into operational or managerial workers and as a function of employment qualification. Same convention as in Figure 2.
Figure 4
Figure 5
Ordinary least square regression to a linear (A) or polynomial (B) function of employment duration only. Empty circles are data points; black stars are predictions (corresponding to the closest integer associated with the linear or polynomial formula); and solid lines show a continuous model (linear or polynomial). The dashed line in (A) corresponds to the rule of thumb. The bottom figure shows the error analysis for each model and in particular the median error of 2.36 and 2.25 months respectively.
A
Pearson’s correlation
B
Prediction error
Prediction error shows a clear decay, in average, as a function of qualification: notice periods are longer for more qualified individuals. Similarly, longer notice periods were awarded to managers. Eventually, notice periods also became increasingly generous over the years (plot showing average prediction error per decade, starting in 1960).
Figure 7
Figure 8
Influence of age in the adjustment of notice period.[74] Prediction error for each data point (circles) as a function of age (bar: mean prediction error, arrowed line: standard deviation) (left); regression to a multivariate polynomial as a function of duration and age (right).
Figure 9
Figure 10
Figure 11
Liste des tableaux
Table 1