Corps de l’article

1. Introduction

Les municipalités cherchent de plus en plus à minimiser les impacts liés aux rejets de polluants au milieu naturel en interceptant la masse maximale de pollution. La capacité de traitement des eaux pluviales dans un réseau d’assainissement unitaire est limitée, en général 2 à 10 fois le débit de temps sec, alors que le ruissellement en temps de pluie peut dépasser de 100 fois ce débit (BENNIS et al., 2001). La connaissance du pollutogramme associé à un événement pluvieux apparaît indispensable afin de maximiser l’interception de polluants dans le cas d’une gestion en temps réel du réseau ou afin de connaître la quantité de polluants rejetés au milieu naturel dans le cas d’une gestion en temps différé.

En général, les matières en suspension (MES) sont le vecteur principal de la pollution des eaux de ruissellement en milieu urbain (CHEBBO et BACHOC, 1992; JACK et al., 1996). Ainsi, l’estimation des quantités de matière en suspension lessivées à l’exutoire d’un bassin versant permet d’estimer le niveau de pollution des eaux de ruissellement (TSIHRINTZIS et HAMID, 1997).

Le cycle des particules solides sur un bassin urbain est un processus complexe. Ce cycle comprend une phase d’accumulation des particules solides sur le bassin en période de temps sec et une phase de lessivage des particules solides en temps de pluie. Les modèles de lessivage des eaux de ruissellement s’attachent à décrire séparément ou conjointement ces deux phases avec un niveau de complexité variable.

Les modèles d’accumulation les plus utilisés sont asymptotiques. Ils dérivent le plus souvent du modèle exponentiel de ALLEY (1981) employé dans le logiciel SWMM (Storm Water Management Model) mais peuvent également être linéaires (SERVAT, 1984).

Le lessivage des sols en milieu urbain est un phénomène complexe et difficile à appréhender qui a été principalement modélisé à l’aide d’approches conceptuelles. Le modèle conceptuel le plus simple est le modèle de « rating curve » (HUBER et DICKINSON, 1988; TEMIMI et BENNIS, 2002) qui relie la charge de matière en suspension au débit de ruissellement. Le modèle exponentiel du logiciel SWMM (HUBER et DICKINSON, 1988) calcule la charge de matière en suspension lessivée à l’aide du débit de ruissellement et de la masse accumulée de particules. Le modèle de lessivage du logiciel STORM (US ARMY CORPS OF ENGINEERS, 1977), le modèle développé par MOYS et al. (1988) pour le logiciel MOSQUITO, le modèle de lessivage du logiciel HSPF (BICKNELL et al., 1997) et le modèle développé par ZUG et al. (1999) pour le logiciel HORUS prennent également en compte la masse de particules accumulées. Des développements récents ont conduit à l’élaboration de modèles déterministes (DELETIC et al., 1997, 2000). Ces modèles présentent l’avantage de décrire les phénomènes physiques impliqués dans le lessivage des sols. En revanche leur utilisation réclame des données qui sont rarement disponibles ou coûteuses à obtenir. Les charges de matière en suspension peuvent également être calculées à l’aide de modèles statistiques (DRIVER et TROUTMAN, 1989). Malheureusement, ces modèles sont uniquement valides pour les sites où ils ont été développés (JEWELL et ADRIAN, 1978).

Cet article présente un nouveau modèle conceptuel de lessivage des MES en milieu urbain. Le modèle proposé sera validé à l’aide de mesures de MES effectuées sur le terrain. Les résultats du modèle proposé seront comparés aux résultats du modèle exponentiel et du modèle de « rating curve ». De plus, les paramètres du modèle proposé feront l’objet d’une analyse de sensibilité.

2. Représentations du processus d’accumulation

2.1 Problématique de l’accumulation

Les activités industrielles, le transport et l’érosion attribuables aux aléas météorologiques sont des sources d’apport en particules solides. Ces apports de particules s’accumulent à la surface d’un bassin urbain durant la période de temps sec. Le processus d’accumulation des particules est un phénomène physique complexe soumis à différentes interprétations. Trois approches distinctes existent pour décrire le processus d’accumulation. La première consiste à considérer l’accumulation variable dans le temps. La masse de solides accumulés est fonction du temps écoulé depuis le dernier événement pluvieux. Cette accumulation est généralement décrite à l’aide de l’équation suivante :

où Ma représente la masse de particules solides accumulées (kg); ACCU, le taux d’accumulation journalier (kg/j); DISP, le coefficient de disparition des particules (j-1). L’accumulation de particules se fait durant la période de temps sec de manière exponentielle jusqu’à atteindre une valeur limite asymptotique. SARTOR et al. (1974) ont montré que l’accumulation maximale est atteinte après environ dix jours mais cette valeur varie grandement en fonction des bassins. Des relations linéaires entre la masse accumulée et le temps ont également été élaborées. Ces relations ont donné dans certains cas de bons résultats (BARBE et al., 1996).

La seconde approche consiste à considérer l’accumulation comme un phénomène instantané. La masse accumulée de particules est reconstituée instantanément à la fin d’un événement pluvieux. Cette approche permet de simplifier la formulation des modèles de lessivage.

Enfin, la dernière approche consiste à considérer que l’accumulation est infinie. Dans ce cas, la masse accumulée de particules est supposée infinie. Cette approche permet également de simplifier la formulation des modèles de lessivage.

2.2 Choix d’un modèle d’accumulation

Le choix d’un modèle d’accumulation est toujours délicat puisqu’il consiste à déterminer l’approche existante la mieux adaptée pour décrire le processus d’accumulation. Afin de faciliter ce choix, il est possible de considérer le bassin urbain comme une juxtaposition de surfaces imperméables et perméables. Les surfaces perméables, constituées de sols granuleux naturels ou aménagés, peuvent être vues comme des réserves inépuisables de particules solides. Cette hypothèse se justifie parfaitement puisque les particules solides sont la matière constituante de ces surfaces. Les surfaces perméables correspondent donc à des zones d’accumulation infinie.

L’accumulation sur les surfaces imperméables s’avère beaucoup plus difficile à appréhender. GROMAIRE (1998) a montré l’existence du lessivage sur les chaussées urbaines et SARTOR et al. (1974) a mis en évidence l’existence d’une accumulation durant la période de temps sec. Or, les études statistiques de KANSO et al. (2005) montrent que la période de temps sec n’a pas d’effet sur le processus d’accumulation. De plus, les analyses de BUTLER et al. (1992) sur des mesures réalisées dans six sites différents ne font ressortir aucune dépendance entre la masse de particules solides accumulées et la masse de particules solides lessivées. Par conséquent, les surfaces imperméables semblent se comporter comme des zones d’accumulation infinie où la perte de particules solides est instantanément compensée par un apport équivalent. Cet apport provient des actions climatiques et des activités humaines

Les contradictions entre les auteurs sur la nature du processus d’accumulation sur les surfaces imperméables s’expliquent par la complexité des phénomènes physiques en jeu. De plus amples études semblent donc nécessaires en vue de lever les ambiguïtés existantes.

3. Formulation du modèle RQSM

3.1 Modèle de mise en suspension des particules solides

Le modèle de mise en suspension repose sur les hypothèses suivantes :

  • l’accumulation est infinie sur les surfaces imperméables et perméables;

  • l’intensité de la pluie est uniforme sur le bassin;

  • l’arrachement des particules solides dépend de l’énergie cinétique des précipitations (YOUNG et WIERSMA, 1973).

SALLES et al. (2002) ont démontré analytiquement que la relation la plus appropriée pour calculer l’énergie cinétique des précipitations en fonction de leur intensité est la suivante :

où KE représente l’énergie cinétique de la pluie par unité de surface et de temps (J·m‑2·h-1); α et β, des paramètres liés aux processus microscopiques de formation des gouttes de pluie; I, l’intensité de la pluie (mm/h). De plus, SALLES et al. (2002) ont montré que l’équation 2 était physiquement réaliste pour des valeurs de α comprises entre 9,2 et 13,5 et pour des valeurs de β comprises entre 1 et 1,4. Par conséquent, l’hypothèse d’accumulation infinie conduit à exprimer le taux de mise en suspension par unité de surface imperméable à l’aide de l’équation suivante :

où mpimp représente le taux de mise en suspension des particules solides par unité de surface imperméable (kg·m-2·s-1); Kpimp, le coefficient de mise en suspension des particules solides pour les surfaces imperméables (kg/J).

La mise en suspension des particules solides sur les surfaces perméables est également fonction de l’énergie cinétique de la pluie. Elle débute lorsque l’intensité de la pluie est supérieure à la capacité d’infiltration des surfaces perméables. Le taux de mise en suspension par unité de surface perméable est donné par l’équation suivante :

où mpper représente le taux de mise en suspension des particules solides par unité de surface perméable (kg·m-2·s-1); Kpper, le coefficient de mise en suspension des particules solides pour les surfaces perméables (kg/J); f, la capacité d’infiltration des surfaces perméables (mm/h).

Les équations 3 et 4 montrent que la mise en suspension des particules solides est contrôlée par le paramètre Kpimp pour les surfaces imperméables et par le paramètre Kpper pour les surfaces perméables. De plus, le taux de mise en suspension mpper fourni par l’équation 4 est nul lorsque f(t) ≥ I(t).

3.2 Modèle de transport des particules solides

Les MES sont physiquement transportées à l’exutoire par le débit de ruissellement. Ce processus de transport des MES peut être modélisé à l’aide de la théorie des systèmes linéaires (CHOW et al., 1988) et des hypothèses physiques suivantes :

  • la réponse impulsionelle du bassin est rectangulaire. De plus elle a une durée égale au temps de concentration du bassin;

  • le temps de concentration pour les particules solides et liquides est identique;

  • le transport des MES sur les surfaces perméables est indépendant du transport des MES sur les surfaces imperméables.

La théorie des systèmes linéaires a été originellement utilisée pour modéliser le ruissellement à la surface des bassins. D’après CHOW et al. (1988), le débit de ruissellement à l’exutoire d’un bassin est donné par le produit de convolution entre l’intensité nette des précipitations et la réponse impulsionnelle du bassin

où Q représente le débit de ruissellement à l’exutoire du bassin (m3·s-1); Inette, l’intensité nette des précipitations (m·s-1); u, la réponse impulsionnelle du bassin (m2·s-1); t, le temps (s).

L’utilisation de la concentration de MES dans la lame d’eau de ruissellement permet de transformer le modèle de ruissellement formulé selon l’équation 5 en un modèle de transport des MES. Ce modèle de transport des MES est donné par l’équation suivante :

où ml représente la charge de matière en suspension (kg/s); C, la concentration de MES dans la lame d’eau de ruissellement (kg·m-3). Or, la multiplication de l’intensité nette des précipitations par la concentration de MES dans la lame d’eau de ruissellement est égale au taux de mise en suspension des particules solides par unité de surface. Par conséquent, l’équation 6 peut s’écrire de la manière suivante :

où mp représente le taux de mise en suspension des particules solides par unité de surface (kg·m-2·s-1).

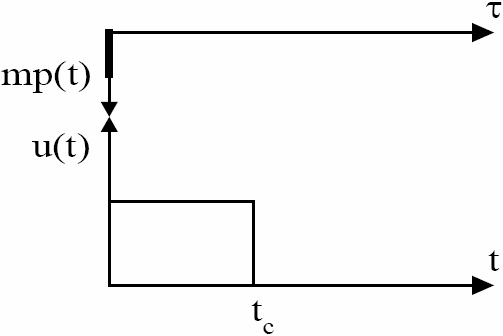
La figure 1 montre que la durée de la réponse impulsionnelle d’un bassin est égale au temps de concentration tc du bassin. Or, le temps de concentration varie en fonction de la pente, de la rugosité et de la longueur de drainage du bassin (CHOW et al., 1988). Par conséquent, le modèle de transport décrit par l’équation 7 prend en compte l’influence des caractéristiques physiques du bassin sur le transport des MES.

Figure 1

Réponse impulsionnelle d’un bassin.

Impulse response function of a catchment.

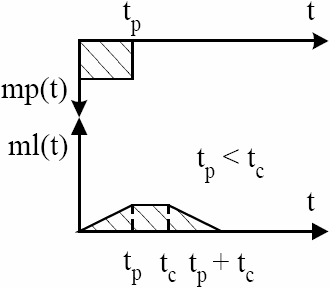
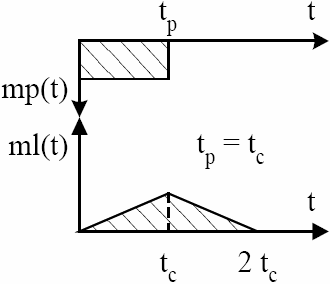
Réponse impulsionnelle d’un bassin.

-> Voir la liste des figures

La figure 2 présente trois pollutogrammes différents calculés à partir de l’équation 7 en considérant mp constant. Les pollutogrammes changent en fonction de la relation de supériorité entre la durée du processus de mise en suspension tp et le temps de concentration tc du bassin. Le premier pollutogramme correspond au cas tp < tc. Dans ce cas, la charge de MES simulée augmente jusqu’à tp. À cet instant, une proportion tp/tc du bassin contribue à l’exutoire. Ensuite, la charge reste constante jusqu’à tc grâce à la contribution fournie par la partie supérieure du bassin. Le second pollutogramme correspond au cas tp = tc. Dans ce cas, la charge de MES augmente jusqu’à tc. À cet instant, la charge est maximale puisque l’ensemble du bassin contribue à l’exutoire. Le dernier pollutogramme correspond au cas tp > tc. Dans ce cas, la charge de MES augmente jusqu’à tc. Ensuite, la charge reste constante jusqu’à tp puisque la mise en suspension se poursuit après tc, sur l’ensemble du bassin. L’étude des pollutogrammes résultant de l’application de l’équation 7 amène deux commentaires. Premièrement, la masse de MES générée par l’équation 7 est toujours égale à la masse de MES mise en suspension. De plus, la durée du pollutogramme simulé est toujours égale à la somme de tp et tc.

Figure 2

Réponses d’un bassin à un taux de mise en suspension de durée tp lorsque : (a) tp < tc, (b) tp = tc et (c) tp > tc.

Catchment responses to an erosion rate of duration tp when: (a) tp < tc, (b) tp = tc and (c) tp > tc.

(a)

(b)

(c)

-> Voir la liste des figures

Les hauteurs de précipitation sont généralement mesurées à pas de temps variables. Elles sont ensuite échantillonnées à pas de temps constants et transformées en intensités. Par conséquent, mp est discrétisé avec le même pas de temps que l’intensité des précipitations. En choisissant un pas de temps d’échantillonnage unitaire de durée 1 minute, le produit de convolution entre le taux de mise en suspension par unité de surface et la réponse du bassin est donné par l’équation suivante :

avec

et

où uimp représente la réponse impulsionnelle des surfaces imperméables (m2/min); uper, la réponse impulsionnelle des surfaces perméables (m2/min); A, la superficie du bassin versant (ha); IMP, la fraction de surface imperméable directement drainée; tc, le temps de concentration du bassin versant (min); n et i, des indices de temps; np, l’indice final du vecteur des taux de mise en suspension par unité de surface. Les conditions mpimp (i) ≥ 0 , mpper (i) ≥ 0 doivent être respectées dans l’équation 8. De plus, la notation n ≤ np sur la borne supérieure de la sommation indique que la sommation s’effectue de i = 1 à n pour n ≤ np et de i = 1 à np pour n > np.

Trois remarques sont à faire à propos du modèle RQSM. Premièrement, le modèle RQSM dissocie la contribution des surfaces imperméables et perméables. Deuxièmement, le modèle RQSM utilise uniquement l’intensité des précipitations pour décrire le transport des MES. Enfin, la représentativité du modèle RQSM est liée à la précision de la mesure des intensités de précipitation. Par conséquent, une résolution inférieure ou égale à cinq minutes est recommandée pour la mesure des intensités de précipitation.

4 . Modèle de « rating curve » et modèle exponentiel

Le modèle de « rating curve » et le modèle exponentiel (HUBER et DICKINSON, 1988) sont des modèles conceptuels éprouvés (TSIHRINTZIS et HAMID, 1997) qui permettent de calculer les charges de MES à l’exutoire d’un bassin urbain. Ces deux modèles ont été retenus pour fin de comparaison et d’évaluation de la performance du modèle RQSM.

Le modèle de « rating curve » relie la charge de matière en suspension lessivée au débit de ruissellement par l’intermédiaire d’une courbe de tarage (« rating curve ») ayant pour expression :

où ml représente la charge de matière en suspension (kg/s); Q, le débit de ruissellement (m3/s); a, le coefficient de lessivage; b, le coefficient d’ajustement.

Le modèle de « rating curve » utilise le débit de ruissellement comme seule variable explicative du phénomène de lessivage. Cette formulation a une base physique. En effet, l’augmentation du débit de ruissellement se traduit par l’augmentation de la contrainte hydraulique de cisaillement à l’interface liquide-solide. Or, la contrainte hydraulique de cisaillement contrôle le potentiel d’arrachement des particules solides sur le bassin. Ce modèle est souvent utilisé comme alternative à des modèles plus complexes lorsque les mesures de charges sont peu nombreuses.

Le modèle de lessivage exponentiel est le modèle utilisé dans le logiciel SWMM. Ce modèle prend en compte la masse accumulée de particules solides. Le calcul de la charge de matière en suspension lessivée par les eaux de ruissellement se fait à l’aide de l’équation suivante :

où ml représente la charge de matière en suspension (kg/s); Ma, la masse de particules solides accumulées (kg); Q, le débit de ruissellement (m3/s); k, le coefficient de lessivage; r, le coefficient d’ajustement. Au cours d’un événement pluvieux, l’évolution de la masse de particules accumulées s’exprime sous la forme :

En supposant un modèle d’accumulation instantanée comme le recommande KANSO et al. (2005), l’accumulation initiale Ma(0) en début de pluie devient un paramètre supplémentaire à caler.

5. Validation du modèle RQSM

5.1 Les sites

Le modèle RQSM, le modèle de « rating curve » et le modèle exponentiel ont été calés et validés à l’aide de 285 mesures de charge de MES. Ces mesures ont été réalisées durant quatre événements pluvieux (BENNIS, 2000) enregistrés à l’exutoire du sous-bassin (1) de l’arrondissement de Verdun situé sur l’île de Montréal (Canada) et de 18 événements pluvieux (NOEL et al., 1987) enregistrés à l’exutoire de trois sous-bassins situés dans la ville de Champaign aux États-Unis. Pour ces 22 événements pluvieux, l’intensité et le débit à l’exutoire des bassins ont été mesurés au pas de temps de 5 minutes. La figure 3 montre que les pluies enregistrées sur les trois sous-bassins de la ville de Champaign ont une période de retour inférieure à 0,5 an et les pluies enregistrées sur le sous-bassin de Verdun ont une période de retour inférieure à 2 ans. Ces pluies ne sont pas des événements exceptionnels. Par conséquent, le calcul de l’énergie cinétique des précipitations a été réalisé suivant les recommandations de SALLES et al. (2002) en prenant α égale à 11 et β égale à 1,24. De plus, le calcul de la capacité d’infiltration des surfaces perméables a été réalisé à l’aide du modèle de Horton modifié (HUBER et DICKINSON, 1988). Ce modèle, couramment utilisé en milieu urbain, tient compte de la capacité initiale d’infiltration du sol (f0), de la capacité finale d’infiltration (f∞) et de la décroissance temporelle de la capacité d’infiltration (K).

Figure 3

Pluies enregistrées sur, (a), le sous-bassin (1) de l’arrondissement de Verdun et sur (b), les sous-bassins Mattis Nord, Mattis Sud et Saint John Nord (Champaign, USA).

Rainfall monitored in (a) the subcatchment (1) of the Verdun borough and (b) the North Mattis, South Mattis and St John North subcatchments (Champaign, USA).

(a)

(b)

-> Voir la liste des figures

Le tableau 1 décrit les caractéristiques physiques des sous-bassins étudiés. Les surfaces, les pentes et l’occupation des sols varient sensiblement d’un sous-bassin à l’autre. La surface des sous-bassins, la fraction de surface imperméable directement drainée, la pente des sous-bassins et les paramètres d’infiltration du modèle de Horton des sous-bassins de Champaign ont été évalués lors des campagnes de mesures. En revanche, les paramètres du modèle de Horton pour le sous-bassin de Verdun et le temps de concentration pour l’ensemble des sous-bassins n’ont pas été mesurés durant les campagnes de mesures. Par conséquent, les valeurs de ces caractéristiques physiques ont été estimées à l’aide d’un modèle hydrologique (BENNIS et CROBEDDU, 2005). Elles peuvent également être obtenues à l’aide de formules ou de valeurs tabulées (CHOW et al., 1988).

Tableau 1

Caractéristiques physiques des quatre sous-bassins utilisés pour la validation du modèle RQSM.

Physical characteristics of the four urban subcatchments used in the RQSM validation.

Bassins

Occupation des sols

A

(ha)

IMP

tc

(min)

Pente

(m/m)

f0

(mm/h)

f∞

(mm/h)

K

(h‑1)

Verdun

Résidentiel

177,0

0,39

37

0,005

85

25

2

Mattis Nord

Commercial

6,8

0,58

30

0,004

200

33

2

Mattis Sud

Commercial

11,2

0,40

18

0,010

200

33

2

Saint John Nord

Résidentiel

22,1

0,19

24

0,006

200

33

2

-> Voir la liste des tableaux

5.2 Calage des trois modèles de lessivage

Les paramètres à caler sont les coefficients de mise en suspension Kpimp et Kpper pour le modèle RQSM, les paramètres a et b pour le modèle de « rating curve » et les paramètres Ma(0), k et r pour le modèle exponentiel.

La performance d’un modèle de simulation peut être évaluée à l’aide des trois indicateurs suivants :

• le coefficient de Nash :

La précision de la charge lessivée simulée est d’autant plus grande que le Nash est proche de l’unité. En hydrologie urbaine, une simulation précise du débit ruisselé conduit à un Nash supérieur à 0,8. Pour la simulation de la qualité des eaux de ruissellement, ce seuil peut être abaissé à 0,6 en raison des nombreuses incertitudes entourant la mesure des polluants (BERTRAND-KRAJEWSKI et al., 2000) et de la complexité des mécanismes physiques à modéliser.

• le rapport des masses :

• le rapport des pointes :

Le coefficient de Nash a été retenu comme critère de calage parce qu’il permet de mesurer le niveau de concordance entre les charges mesurées et simulées. Ainsi, le calage des modèles a consisté à choisir la valeur des paramètres qui maximise le nombre de Nash. Le choix optimal des paramètres a été réalisé à l’aide de l’algorithme du simplex (LAGARIAS et al., 1998) implémenté dans le logiciel MATLAB.

Les trois modèles de lessivage des MES ont été calés sur le sous-bassin (1) de l’arrondissement de Verdun à l’aide de deux pollutogrammes mesurés. Pour les trois autres sous-bassins, le nombre plus important d’événements mesurés a permis de caler les modèles à l’aide de trois pollutogrammes. Dans le cas du bassin de Verdun, un événement dont l’intensité ne dépassait pas la capacité d’infiltration des surfaces perméables a été utilisé pour caler le paramètre Kpimp. Par la suite, un événement dont l’intensité dépassait la capacité d’infiltration des surfaces perméables a été utilisé pour caler le paramètre Kpper. En effet, un événement présentant une faible intensité ne sature pas le sol des surfaces perméables. Par conséquent, seules les surfaces imperméables sont lessivées. En revanche, un événement présentant une forte intensité sature le sol des surfaces perméables engendrant le lessivage des surfaces perméables et imperméables. Pour les trois sous-bassins de la ville de Champaign, les événements pluvieux n’étaient pas suffisamment importants pour faire contribuer les surfaces perméables. Par conséquent, seul le coefficient Kpimp a été calé. Le tableau 2 fournit les valeurs après calage des paramètres des modèles RQSM, « rating curve » et exponentiel.

Tableau 2

Valeur des paramètres après calage des modèles RQSM, « rating curve » et exponentiel.

Parameter values after the calibration of the RQSM, rating curve and exponential models.

 

« Rating Curve »

Modèle Exponentiel

RQSM

Bassins

a

b

Ma(0)

(kg)

k

r

Kpimp

(kg/j)

Kpper

(kg/j)

Verdun

8,45·10‑2

1,29

2 963

9,89·10‑2

1,14

7,66·10‑6

1,80·10‑5

Mattis Nord

1,41

1,46

552

8,27

1,13

2,84·10‑5

-

Mattis Sud

1,05

1,44

100

38,54

1,36

7,57·10‑6

-

Saint John Nord

2,26

2,15

273

112,25

2,88

1,41·10‑5

-

-> Voir la liste des tableaux

La valeur des paramètres obtenus appelle deux commentaires. Premièrement, la masse accumulée Ma(0) du modèle exponentiel et le coefficient de mise en suspension Kpimp du modèle RQSM ne semblent pas être corrélés à la surface des sous-bassins ou à l’occupation des sols présentées au tableau 1. Deuxièmement, le paramètre k du modèle exponentiel présente de fortes variations entre les différents sous-bassins. Ces variations s’expliquent en grande partie par l’utilisation d’un modèle d’accumulation instantanée. En effet, les paramètres des modèles RQSM et « rating curve » ont une amplitude de variation moindre que le modèle exponentiel alors qu’ils utilisent un modèle d’accumulation infinie.

5.3 Comparaison des trois modèles de lessivage

Les pollutogrammes de MES fournis par le modèle RQSM, le modèle exponentiel et le modèle de « rating curve » ont été comparés aux 11 pollutogrammes mesurés restants. La valeur des indicateurs de performance après simulation est fournie au tableau 3. Le coefficient de Nash est supérieur à 0,6 pour six événements simulés à l’aide du modèle exponentiel et pour cinq événements simulés à l’aide du modèle RQSM et « rating curve ». Par conséquent, les trois modèles ont fourni un pollutogramme proche du pollutogramme mesuré pour 50 % des événements mesurés. L’erreur sur la masse de MES lessivée est inférieure à 30 % pour six événements simulés à l’aide du modèle RQSM et « rating curve » comparativement à trois événements simulés à l’aide du modèle exponentiel. Par conséquent, le modèle RQSM a modélisé la masse de MES lessivée de manière équivalente au modèle de « rating curve » mais mieux que le modèle exponentiel. L’erreur sur la pointe du pollutogramme est inférieure à 30 % pour huit événements simulés à l’aide du modèle exponentiel et pour six événements simulés à l’aide du modèle RQSM et « rating curve ». Par conséquent, le modèle RQSM a modélisé la pointe du pollutogramme de manière équivalente au modèle de « rating curve » mais moins bien que le modèle exponentiel.

Tableau 3

Valeurs des indicateurs de performance lors de la validation des modèles RQSM, « rating curve » (RC) et exponentiel (EXP).

Performance criteria values from the simulation of particle loads with the RQSM, rating curve (RC) and exponential (EXP) models.

Événements

Nash

RM

RP

RC

EXP

RQSM

RC

EXP

RQSM

RC

EXP

RQSM

V. 30-09-99

‑0,05

0,48

0,25

0,71

0,99

0,66

0,51

0,55

0,56

V. 13-10-99

0,49

0,06

0,70

0,85

1,36

0,98

0,74

1,16

1,02

M. N. 17-05-80

0,81

0,85

0,46

1,23

1,44

0,79

0,87

1,03

0,64

M. N. 23-05-80

‑2,39

0,12

0,89

3,22

2,24

1,13

2,49

1,56

1,24

M. N. 01-06-80

‑1,47

‑2,14

0,42

2,80

3,02

1,54

1,75

2,26

0,99

M. S. 01-06-80

‑0,22

0,92

0,52

2,37

1,32

1,29

1,97

1,26

0,69

M. S. 23-06-80

‑1,19

0,51

0,88

2,31

0,63

0,99

2,34

1,02

0,90

M. S. 28-06-80

0,73

0,98

‑0,07

1,43

0,92

0,47

1,06

0,91

0,19

S. J. N. 17-05-80

0,88

0,80

0,65

0,76

0,58

1,50

0,95

0,86

1,21

S. J. N. 30-05-80

0,90

0,76

0,88

0,73

0,54

1,03

0,94

0,81

0,82

S. J. N. 01-06-80

0,88

0,79

0,26

0,89

0,83

1,48

1,09

1,20

0,66

-> Voir la liste des tableaux

Les figures 4 et 5 présentent deux événements simulés par le modèle RQSM, exponentiel et « rating curve ». Ces deux événements montrent que la corrélation entre le hyétogramme et le pollutogramme n’est pas indispensable pour que le modèle RQSM fournisse de bons résultats. En revanche, une bonne corrélation entre hydrogramme et pollutogramme permet au modèle exponentiel et « rating curve » de bien reproduire la forme du pollutogramme. Néanmoins, elle n’est pas synonyme d’une bonne estimation de la charge de MES lessivée comme le montre la figure 5 pour le modèle de « rating curve ».

Figure 4

(a) Pluie et débit du 13 octobre 2000 sur le sous-bassin (1) de l’arrondissement de Verdun, et (b) charges de MES mesurées et simulées.

(a) Rainfall and flow in the subcatchment (1) of the Verdun borough on 13 October 2000, and (b) measured and simulated TSS loads.

(a)

(b)

-> Voir la liste des figures

Figure 5

(a) Pluie et débit du 23 juin 1980 à South Mattis, et (b) charges de MES mesurées et simulées.

(a) Rainfall and flow in South Mattis on 23 June1980, and (b) measured and simulated TSS loads.

(a)

(b)

-> Voir la liste des figures

La comparaison des trois modèles sur la base de résultats événementiels peut être trompeuse puisqu’elle masque la présence de disparités ou de biais dans les résultats. Afin d’avoir une vision plus représentative de la performance des modèles RQSM, exponentiel et « Rating Curve », la valeur moyenne des indicateurs de performance et leur écart-type sont présentés au tableau 4. Le nombre d’événements simulés n’apparaît pas suffisant pour pouvoir statistiquement prouver la supériorité d’un modèle sur un autre. Néanmoins, quelques remarques qualitatives peuvent être émises. Premièrement, les trois modèles ne simulent pas parfaitement les pollutogrammes de MES. En effet, le Nash moyen pour l’ensemble des événements simulés est inférieur à 0,6. Deuxièmement, le modèle exponentiel et le modèle de « rating curve » ont surestimé la charge lessivée. En effet, le RM moyen est proche de 1 pour le modèle RQSM alors qu’il est de 1,26 pour le modèle exponentiel et de 1,57 pour le modèle de « rating curve ». Troisièmement, le modèle RQSM a sous estimé le rapport des pointes alors que le modèle exponentiel et le modèle de « rating curve » le surestime. Enfin, les trois modèles de lessivage présentent des performances très variables. En effet, les écarts types sur le Nash, Rp et RM s’échelonnent de 0,31 à 1,14. Ces résultats mitigés sont la conséquence de quatre sources d’incertitudes différentes. La première source d’incertitude provient de l’incertitude associée aux mesures des précipitations, des débits ruisselés, et surtout des charges de MES (BERTRAND-KRAJEWSKI et al., 2000). La deuxième source d’incertitude résulte de la méconnaissance des processus d’accumulation des particules solides sur les surfaces imperméables durant la période de temps sec. La troisième source d’incertitude provient de l’absence de description des processus de déposition et de remise en suspension des particules solides durant la phase de transport. Enfin, la quatrième source d’incertitude résulte de l’utilisation des modèles sur des sous‑bassins non uniformes en matière de rugosité, de pente et de distribution des particules solides.

Tableau 4

Moyennes et écarts-types des valeurs de Nash, RP et RM

Means and standard deviations of the Nash, RP and RM values.

Modèles

Nash

RM

RP

Moyenne

Écart-type

Moyenne

Écart-type

Moyenne

Écart-type

« Rating Curve »

‑0,06

1,14

1,57

0,93

1,34

0,68

Modèle Exponentiel

0,33

0,93

1,26

0,77

1,15

0,45

RQSM

0,53

0,31

1,08

0,35

0,81

0,31

-> Voir la liste des tableaux

5.4 Analyse de sensibilité du modèle RQSM

L’analyse de sensibilité a porté sur les paramètres de calage Kpimp, Kpper et sur les paramètres physiques tc, f0, f∞, K. En effet, la valeur mesurée ou calculée de ces quatre paramètres physiques est souvent entourée d’une grande incertitude. La sensibilité de ces six paramètres a été évaluée en considérant le coefficient de Nash.

La démarche retenue a consisté à attribuer des valeurs de référence aux six paramètres étudiés. Ces valeurs de références sont présentées au tableau 5. Elles ont servi à calculer un pollutogramme de référence. Par la suite, une variation a été imposée à une des valeurs de référence du modèle RQSM. Le nouveau pollutogramme ainsi obtenu a été utilisé avec le pollutogramme de référence pour calculer le coefficient de Nash correspondant.

Tableau 5

Valeurs de référence des paramètres pour l’analyse de sensibilité du modèle RQSM

Reference values of the parameters used for the sensitivity analysis of the RQSM model.

Paramètres

A (ha)

IMP

tc

(min)

f0

(mm/h)

f∞

(mm/h)

K

(1/h)

Kpimp

(kg/j)

Kpper

(kg/j)

Valeurs

100

0,5

32

160

16

4

2·10‑5

2·10‑5

-> Voir la liste des tableaux

L’analyse de sensibilité a été menée à l’aide des deux pluies suivantes :

  • pluie (1) : I = 10 mm/h; durée : 240 min.

  • pluie (2) : I = 80 mm/h; durée : 25 min.

La pluie (1) génère une hauteur d’eau inférieure à la capacité d’infiltration des surfaces perméables définie par les paramètres de référence du modèle RQSM. En revanche, la pluie (2) génère une hauteur d’eau supérieure à la capacité d’infiltration des surfaces perméables. Par conséquent, la pluie (1) lessive uniquement les surfaces imperméables alors que la pluie (2) lessive les surfaces perméables et imperméables.

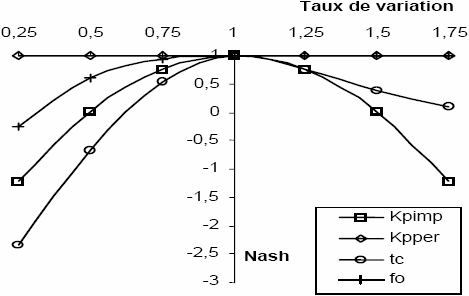
Les résultats de l’analyse de sensibilité pour la pluie (1) sont présentés à la figure 6(a). Ils amènent deux remarques importantes. Premièrement, la variation du paramètre Kpimp engendre une forte augmentation du coefficient de Nash. Par conséquent, Kpimp doit être minutieusement calé. Enfin, la variation du temps de concentration engendre une faible diminution du Nash. Par conséquent, une valeur approchée de tc peut être utilisée pour les pluies de faible intensité et de durée supérieure à tc.

Figure 6

Variation du Nash en fonction du taux de variation des paramètres du modèle RQSM pour (a), la pluie (1), et (b), la pluie (2).

Variation of the Nash value as a function of the rate of change of the RQSM parameters for (a), rainfall (1), and (b), rainfall (2).

(a)

(b)

-> Voir la liste des figures

Les résultats de l’analyse de sensibilité pour la pluie (2) sont présentés sur la figure 6(b). Ils amènent quatre remarques importantes. Premièrement, la variation du paramètre Kpimp engendre une forte diminution du Nash comme pour la pluie (1). En revanche, la variation du paramètre Kpper ne fait pratiquement pas diminuer le Nash. Néanmoins, ce paramètre peut devenir influent en cas de pluie extrême ou pour une surface perméable présentant une faible capacité d’infiltration. Deuxièmement, la variation de tc, dans le cas d’une pluie de durée supérieure à tc, génère une plus grande diminution du Nash que la variation de Kpimp. En revanche, l’influence de tc diminue significativement et devient même inférieure à celle de Kpimp quant la durée de la pluie est inférieure à tc. Troisièmement, une variation importante de la capacité initiale d’infiltration (f0) entraîne une importante baisse du Nash. De plus, la sous-estimation de la capacité initiale d’infiltration entraîne une diminution du Nash plus importante que sa surestimation. Enfin, la variation de la capacité finale d’infiltration (f∞) et du coefficient de décroissance (K) a entraîné une diminution négligeable du Nash. Par conséquent, la variation de ces paramètres n’a pas été présentée sur la figure 6(b) afin d’en alléger la lecture. Ces résultats sur les paramètres d’infiltration du modèle de Horton sont similaires aux observations faites suite à l’analyse de sensibilité du modèle de réservoir non linéaire du logiciel SWMM (LIONG et al., 1991).

6. Conclusion

Le présent article a mis en lumière une approche conceptuelle originale pour modéliser la charge de matière en suspension lessivée sur les bassins urbains. L’originalité du modèle RQSM découle, d’une part, de l’utilisation de l’énergie cinétique des précipitations pour modéliser la mise en suspension des particules solides, et, d’autre part, de l’emploi de la théorie des systèmes linéaires pour décrire le transport des MES à la surface du bassin.

Le modèle RQSM présente trois atouts. Premièrement, il utilise uniquement l’intensité des précipitations pour calculer la charge de MES lessivée à l’exutoire d’un bassin urbain. Deuxièmement, il dissocie la contribution en MES des surfaces perméables et imperméables. Enfin, seuls deux paramètres du modèle RQSM nécessitent un calage.

Le modèle RQSM a simulé les charges de MES mesurées, à l’exutoire de quatre sous-bassins urbains situés en Amérique du Nord, avec un niveau de précision équivalent à celui de deux modèles conceptuels éprouvés. L’analyse de sensibilité du modèle RQSM a montré que deux paramètres avaient un impact significatif sur le pollutogramme simulé.

Les résultats encourageants obtenus à l’aide du modèle RQSM permettent d’envisager une extension de son utilisation à d’autres polluants.