Simulation du bilan hydro–sédimentaire d’un barrage collinaire en zone marneuse méditerranéenne (Cas du barrage Saboun, Maroc) Simulation of the hydro-sedimentary balance assessment of a little dam in Mediterranean marly zone (Saboun’s dam, Morocco)

Résumé

La présente étude a pour objectif de suivre et de simuler les apports en eau et en sédiments dans un barrage collinaire, en utilisant un modèle hydrologique de type physique distribué permettant le calcul de l’écoulement et de l’érosion des petits bassins versants marneux.

Le modèle utilisé est le modèle « Mina », transposé dans cette étude au bassin versant marneux de Saboun situé au nord-ouest du Maroc, équipé d’un petit barrage en son exutoire et d’un très petit lac collinaire dans sa partie amont. La simulation est basée sur un découpage du bassin versant en unités hydrologiques homogènes dont les valeurs des paramètres de l’infiltration sont déduites d’expérimentations de simulation de pluies à l’échelle du mètre carré. Le calage et la validation du modèle sont effectués par confrontation des sorties du modèle aux mesures hydrologiques et bathymétriques réalisées au niveau de la retenue aval entre 1997 et 1999.

Cette confrontation a montré que le modèle « Mina » sous-estime l’écoulement pour des sols très humides et le surestime pour des sols secs. Cette surestimation est expliquée par la fissuration des sols marneux à l’état sec. La sous-estimation s’explique par le colmatage rapide des sols marneux à l’état humide. Pour réduire ce biais, une augmentation de la perméabilité initiale doit être appliquée pour les sols secs à faible indice d’humidité IK et une diminution de la perméabilité finale doit être appliquée pour les sols humides à fort indice d’humidité IK. Ces rectifications ont permis l’amélioration de l’estimation des volumes simulés et une meilleure estimation de l’envasement de la retenue du barrage Saboun.

Mots clés:

• barrage collinaire,
• simulation,
• bilan hydro–sédimentaire,
• écoulement,
• envasement,
• sols marneux,
• infiltration

Abstract

The objective of the present study was to monitor and simulate the water and sediment balance in a small dam, by using a distributed physical hydrological model to estimate the outflow and the erosion rate of a small marl watershed.

The “Mina” model was applied to the Saboun watershed, which is located in north-western Morocco and contains a small dam at its outlet. The simulation was based on the partitioning of the watershed into homogeneous hydrological units, and on infiltration and humidity parameter values deduced from rainfall simulation experiments. The model was validated by comparing the simulated data to hydrological and sedimentation data measured between 1997 and 1999.

The analysis of this comparison showed that the model underestimated the watershed outflows for rainfall events that had a high antecedent humidity index (IK > 15 mm), and overestimated the outflows for rainfall events that had a low antecedent humidity index 0 < IK < 15 mm. This observation is explained by the hydrodynamic behaviour of the marl soils, which crack under dry conditions and fill up quickly during wet conditions. To reduce this variability, the initial permeability values were decreased or increased, respectively, for the rainfall events with low and high antecedent humidity indexes. This resulted in the improvement of simulated volumes by about 80% and a better prediction of the water balance and accumulation of silt in the reservoir upstream from the Saboun dam.

Key words:

• small dam,
• simulation,
• sediment and hydrological balance,
• outflow,
• marl soils,
• infiltration

1. Introduction

La gestion des ressources hydriques est une des priorités pour assurer la qualité de vie dans les sociétés actuelles. Au Maroc, cette gestion prend une importance particulière dans le développement du pays étant donné les distributions spatiale et temporelle inégales des précipitations (AGOUSSINE et BOUCHAOU, 2004; ALLOUZI et BOUAAM, 1994). Avec les périodes de sécheresse qui sont devenues de plus en plus fréquentes au cours des dernières décennies, les réservoirs collinaires ont pris une importance accrue dans la politique de gestion des ressources en eau (MAHFOUD, 1989). Au Maroc, plus de 104 lacs et 54 barrages collinaires ont été construits depuis 1980 au cours de différents projets de mobilisation des eaux superficielles. Ils ont été l’oeuvre de deux ministères : le ministère des Travaux publics chargé de l’équipement hydraulique du pays et le ministère de l’Intérieur chargé du programme de lutte contre les effets de la sécheresse.

Si ces ouvrages répondent parfaitement à leurs objectifs nationaux de mobilisation de l’eau, ils souffrent cependant, dans le nord du Maroc, d’un envasement rapide de leurs retenues dû à une forte érosion des sols sur leurs bassins versants, laquelle atteint des taux très élevés, compris entre 24 t•ha^‑1•an^‑1 sur parcelles et 140 t•ha^‑1•an^‑1 sur ravines dans les montagnes du Rif et du Pré-Rif marneux (HEUSH, 1970; MERZOUK et DAHMAN, 1998; TAYAA, 1997). En Afrique du Nord, la perte annuelle en volumes d’eau stockés par envasement des petites retenues est estimée comprise entre 4 et 5 % (ALBERGEL et al., 2003b). Elle est du même ordre de grandeur en Italie pour les petites retenues (GAZZALO et BASSI, 1969). Pour les grands barrages du Maroc, la perte annuelle en volumes d’eau stockés est estimée à 0,5 % (MARZOUKI, 1992).

Au Maroc, la recherche hydrologique à l’échelle des petits bassins versants n’a pas été suffisamment développée pour produire des modèles d’estimation fiables et précis des apports en eau et en sédiments dans les petites retenues (ALBERGEL et al., 2004). Des exemples connus de surdimensionnement et de sous-dimensionnement de la capacité de stockage des ouvrages font que l’estimation des apports hydro-sédimentaires dans les petites retenues est un enjeu économique important. La référence nationale concernant le calcul des débits de projet et le dimensionnement de ces petites retenues souffrent d’importantes lacunes. Les modèles empiriques, Curve Number (CN), modèles rationnels, hydrogramme unitaire, équations universelles de perte en sol MUSLE et RUSLE (WILLIAMS, 1975) donnent des résultats moyens sur des périodes de longue durée mais ne sont pas fiables pour évaluer l’impact d’une évolution du milieu naturel ou des pratiques culturales sur les régimes hydrologiques. Les modèles distribués à base physique sont de plus en plus nombreux et se veulent être de bons outils de simulation et de prévision (AMBROISE, 1999). Ils sont mis au point et testés sur des bassins versants connus pour lesquels on dispose d’importants jeux de données. Ils mettent en jeu de nombreuses variables à l’échelle de la surface concernée, variables qui ne sont pas faciles à déterminer. La calibration, à partir de jeux de données d’entrée et de sortie, est la technique la plus répandue pour s’affranchir des mesures que l’on ne sait pas faire. La validation, effectuée en utilisant d’autres jeux de données d’entrée et de sortie que ceux qui ont été utilisés pour le calage, permet d’évaluer l’adéquation du modèle à simuler le fonctionnement hydrologique du bassin versant.

Des travaux similaires ont été réalisés sur les petits bassins versants au sud de la Méditerranée, en Tunisie et en Algérie (ALBERGEL et al., 2003a; GOMER, 1994). Parmi ces modèles, on trouve le modèle « Mina », spécifiquement adapté aux petits bassins versants marneux, mais il nécessite une validation pour les autres régions d’Afrique du Nord que celle où il a été validé. En effet, le modèle « Mina » a été mis au point, calibré et validé, sur plusieurs petits bassins versants de 40 à 70 ha du grand bassin versant de l’Oued Mina au nord-ouest de l’Algérie (GOMER et al., 1992; GOMER, 1994). L’objectif principal de ce travail est donc de transposer ce modèle au bassin versant du barrage collinaire de l’Oued Saboun situé au nord-ouest du Maroc et de proposer, pour cette région du Rif, un outil de prévision des apports liquides et solides dans les petites retenues artificielles.

L’étude est basée sur un découpage du bassin versant en unités hydrologiques homogènes dont les valeurs des paramètres de l’infiltration sont déduites d’expérimentations in situ, à l’échelle du mètre carré sous simulations de pluies. La validation du modèle est présentée par confrontation des données simulées aux données observées à deux pas de temps : celui de la crue pour les apports liquides et celui de l’année pour les apports solides. Pour la spatialisation et la simulation hydrologique, ce travail utilise les outils des nouvelles technologies de géomatique (SIG) et d’acquisition des données hydrométéorologiques.

2. Matériels et méthodes

2.1 Le bassin versant de l’Oued Saboun

Le présent travail a été conduit sur le petit bassin versant marneux de l’Oued Saboun situé au nord-ouest du Maroc dans le grand bassin versant de l’Oued Tahadart qui draine les eaux de son bassin vers l’océan Atlantique (Figure 1). Un petit barrage en terre, de 15 m de hauteur, a été construit à l’exutoire du bassin versant de l’Oued Saboun. Mise en eau en 1991, sa retenue, d’une capacité de 1 100 000 m³, stocke les eaux de ruissellement afin d’irriguer un petit périmètre en aval de la zone de Fahs, près de la ville de Tanger (Tableau 1).

Figure 1

Situation du site d’étude.

Location of the study site.

Tableau 1

Caractéristiques des retenues de Saboun et de Daimos et de leurs bassins versants.

Characteristics of the Saboun and Daimos dams and their catchment areas.

	Saboun	Daimos
Type	Terre homogène	Terre homogène
Hauteur	15 m	5 m
Longueur de la digue	443 m	90 m
Apport moyen annuel	1 100 000 m3	250 000 m3
Capacité du réservoir	1 100 000 m3	30 000 m3
Surface du bassin versant	802 ha	228 ha
Altitude min du bassin versant	17 m	75 m
Altitude max du bassin versant	130 m	130 m

En amont de ce bassin versant, il existe également un lac collinaire créé en 1991, en même temps que le barrage Saboun, par la construction d’une digue en terre homogène. Ce lac présente une superficie de 1,3 ha à sa cote de déversement. Il est situé à l’exutoire d’un sous-bassin versant d’une superficie de 228 ha appelé Daimos, nom emprunté au village qui occupe la rive droite du sous-bassin. Il joue aussi un rôle de protection contre l’envasement du barrage Saboun. Son déversoir latéral est constitué de deux conduites en ciment de 80 et 40 cm de diamètre. En 1991, ces conduites étaient situées à environ 3,40 m au-dessus du fond de la retenue. En 2005, elles se situaient à 1,25 m du fond de la retenue, ce qui correspond à un envasement de 2,15 m de cette retenue sur la période 1991-2005.

Du point de vue climatique, la région de Tanger est caractérisée par un climat de type méditerranéen sub-humide (BEN ABID, 1982). Elle est considérée comme l’une des régions les plus pluvieuses du Maroc. Calculée sur une période de 30 ans, de 1969 à 1999 à la station de Kalaya, la plus proche du site de Saboun, la moyenne des précipitations annuelles est de 742 mm. La pluviométrie annuelle décennale sèche est de 490 mm, la pluviométrie annuelle décennale humide de 995 mm. Au cours des années sèches, les ressources en eau superficielles de cette région diminuent fortement et ne sont pas compensées par des ressources en eaux souterraines suffisantes, le déficit en eaux superficielles pouvant atteindre un taux très élevé, de l’ordre 84 % pour l’année 1998-99, année vicennale sèche (20 ans) et de 90 % pour l’année 1994-95 (ONEP, 1996). Le déficit en eaux souterraines de la région de Tanger s’explique par le fait qu’une grande partie du substratum de la région (Unité de Tanger) est formée d’argiles et de marnes d’âge Sénonien (TAUVIN, 1971). Les faciès argilo-marneux de l’Unité de Tanger empêchent toute percolation en profondeur, limitant ainsi la formation des nappes d’eaux souterraines. Les seules ressources en eau susceptibles d’être mobilisées en quantité importante sont donc les eaux superficielles dont les écoulements sont essentiellement générés par les fortes pluies.

2.2 Le modèle « Mina »

Le modèle « Mina » est un modèle déterministe semi-physique de type distribué, basé sur les concepts d’infiltration de Horton pour le calcul du ruissellement et d’énergie cinétique des pluies et de l’écoulement pour la production de l’érosion. Les mécanismes de transfert ou de routage sont assurés par l’équation de continuité mono-dimensionnelle de Saint-Venant (GOMER, 1994). C’est un modèle qui a été élaboré dans le but de permettre les quantifications de l’écoulement et de l’érosion des petits bassins versants marneux. Il a été choisi pour simuler les crues et l’érosion du bassin versant de Saboun parce que ses caractéristiques répondent parfaitement aux conditions de la zone d’étude où le processus d’infiltration dominant est a priori de type Hortonien (ALBERGEL et al., 2003a). Il présente en outre les avantages suivants :

• c’est un modèle de type déterministe à base physique;

• c’est un modèle distribué à mailles régulières;

• c’est un modèle événementiel simulant l’écoulement crue par crue;

• c’est un modèle adapté aux zones semi-arides et aux sols marneux; et

• pour un modèle à base physique, c’est un modèle dont le nombre de paramètres est réduit.

Les principales données d’entrée du modèle « Mina » sont la pluie (les cumuls pluviométriques journaliers et les intensités horaires des pluies), la carte des unités hydrologiques, la carte des pentes et celle du réseau hydrographique, le taux d’infiltration et l’humidité du sol avant l’averse et l’énergie cinétique critique d’arrachement des particules du sol.

2.3 Constitution d’un échantillon de données hydrologiques

2.3.1 Équipement hydrométéorologique utilisé

Le barrage Saboun a été équipé d’une station hydrométéorologique automatique (MERZOUK et al., 1997) installée en novembre 1997 sur la digue de la retenue. Elle se compose :

• d’une sonde piézo-résistive immergée permettant d’enregistrer automatiquement les variations de hauteur d’eau du lac à 1 cm près sur un pas de temps de 5 min;

• d’un pluviographe à augets basculeurs permettant d’enregistrer le cumul des précipitations avec une précision de 0,5 mm;

• d’un bac d’évaporation enterré, de type Colorado-ORSTOM, de 1 m² d’ouverture et 60 cm de profondeur, la mesure étant effectuée manuellement chaque matin par l’observateur;

• d’une batterie d’échelles limnimétriques implantées sur la digue;

• d’une centrale d’enregistrement et de mémorisation des données; et

• d’un déversoir calibré permettant de connaître les débits sortant de la retenue sur un pas de temps de 5 min (déversoir de forme rectangulaire de 8 m de largeur). Le déversement a lieu quand l’eau stockée dans la retenue atteint la cote 6,68 m (16,68 m NGM).

Les données limnimétriques et pluviométriques enregistrées sont transférées régulièrement au laboratoire pour établir une base de données hydrométéorologiques.

Le lac Daimos n’a pas été équipé d’une station hydrométrique. Cependant, nous avons considéré que la pluie tombée au niveau de la retenue du barrage Saboun est représentative de la pluie tombée sur l’ensemble du bassin. Par comparaison, le bassin versant de Kalaya (38 km²), situé environ 10 km à l’est, dispose de deux pluviomètres implantés à ses deux extrémités : l’un en aval à une altitude de 45 m (station hydrologique de Kalaya, pluviomètre nommé PKayala) et l’autre en amont à 300 m d’altitude (station de Romane, pluviomètre nommé PRomane). Sur la période 1974-2005, les totaux pluviométriques annuels de ces deux pluviomètres sont bien corrélés, avec un coefficient de corrélation de 0,96 : PKalaya = 0,96 x PRomane avec R² = 0,95. À l’échelle journalière, le coefficient de corrélation entre pluies journalières aux deux stations est encore égal à 0,90 avec R² = 0,78.

2.3.2 Reconstitution d’un échantillon de crues

La détermination du bilan hydrologique de la retenue du barrage Saboun est basée sur l’application de l’équation du bilan qui découle du principe de conservation des volumes d’eau exprimés en m³ (ALBERGEL et al., 1997), soit :

(1)

avec : ∆V la variation du volume, V_r le volume ruisselé, V_ecs le volume des apports souterrains, V_p le volume des apports pluviométriques sur la retenue, V_ev le volume évaporé, V_d le volume déversé, V_vi le volume vidangé, V_i le volume infiltré et V_u le volume utilisé.

Toutes les variables accessibles à l’observation (V_p, V_d, V_vi, V_ev) ont été mesurées pour toute la période comprise entre novembre 1997 et octobre 1999. Le volume ruisselé V_r est la somme des débits entrant dans la retenue, il est obtenu par intégration de l’équation suivante : . Dans la dernière équation, les paramètres sont : Q_r débit ruisselé, Q_d le débit de déversé et Q_p le débit dû à la pluie. Les paramètres non mesurés, le volume infiltré (V_i), le volume des eaux souterraines (V_ecs) et le volume utilisé (V_u), sont globalement appréciés par bouclage du bilan.

Sur un petit pas de temps et durant les crues, il est possible de calculer des débits en dérivant l’équation (1) sur le pas de temps de mesure des volumes d’eau (5 min) et en faisant quelques approximations justifiées. Lors d’une crue de courte durée, les apports souterrains du bassin versant, l’évaporation du plan d’eau, l’infiltration et l’utilisation des eaux de la retenue peuvent être négligés. Ceci permet de reconstituer le ruissellement (ALBERGEL et al., 1997) en simplifiant les calculs du bilan à l’échelle de la crue.

Toutes les crues du bassin versant de Saboun ont été ainsi reconstituées entre novembre 1997 et août 1999 (ABDELLAOUI et al., 2002). Elles ont été représentées sur la figure 2 par leurs débits maximaux et leurs pluies journalières. Chaque crue est caractérisée par une chronique de débits sur un pas de temps de 5 min, un volume total et un débit maximal. La figure 3 présente la crue du 4/12/97, reconstituée à l’exutoire du bassin versant de l’Oued Saboun à partir des enregistrements de hauteurs d’eau du lac. Sur cette même figure, les débits déversés forment une crue très aplatie, fortement laminée par la retenue.

Figure 2

Crues et averses reconstituées à Saboun entre novembre 1997 et août 1999.

Stream flows and rainfall reconstituted at the Saboun dam between November 1997 and August 1999.

Figure 3

Crue du 04/12/1997, reconstituée au barrage de Saboun.

Flood of 04/12/1997, reconstituted at the Saboun dam.

2.4 Mesures de la sédimentation et calcul de l’envasement

La détermination du taux d’envasement de la retenue Saboun est basée sur des mesures ponctuelles de la bathymétrie du lac, complétées par une topographie fine des berges exondées (Figure 4). Le volume total des sédiments piégés entre deux campagnes de mesures bathymétriques est estimé par différence des volumes de la retenue et confrontation des modèles numériques de terrain (MNT) créés à partir des levés bathymétriques et topographiques. La différence des volumes d’eau stockés à la cote normale entre l’année 1991 et la dernière mesure bathymétrique représente la part des sédiments érodés sur le bassin versant et transportés par les eaux de ruissellement jusqu’au barrage de l’Oued Saboun depuis la construction du barrage en 1991 (ALBERGEL et al., 2003b).

Figure 4

Évolution de la bathymétrie entre 1999 et 2004 dans la retenue du barrage Saboun.

Evolution of bathymetry between 1999 and 2004 in the Saboun reservoir.

Les résultats de ce contrôle bathymétrique, en matière de volume total envasé et de taux moyen d’envasement, sont présentés dans le tableau 2. Ils prennent en compte les mesures bathymétriques postérieures à la période considérée et permettent d’observer une certaine constance dans l’envasement de la retenue.

Tableau 2

Données disponibles de bathymétrie à Saboun.

Available bathymetric data for the Saboun reservoir.

	Volume Initial (m3)	Volume Restant (m3)	Volume de vase (m3)	Envasement (Densité de Vase = 1,3) (t•an‑1)	Perte Annuelle (%)
Période 1991‑1999	1 100 000	903 990	196 010	31 852	2,0
Période 1991‑2003	1 100 000	817 240	282 760	28 276	2,0
Période 1991‑2004	1 100 000	801 020	298 986	27 762	1,9

Le volume total des apports en sédiments arrivant au barrage est calculé en tenant compte du volume d’envasement et du volume des sédiments évacués au moment des déversements et des vidanges. Cette partie des sédiments évacués a été estimée en fonction des volumes totaux déversés et vidangés et de leurs concentrations moyennes en sédiments, concentrations déterminées par analyse de quelques échantillons d’eau prélevés au niveau du déversoir et près de la vidange de fond. Les concentrations en sédiments des déversements varient entre 0,01 et 0,12 g•L^‑1, avec une moyenne de 0,06 g•L^‑1. Cette faible concentration en sédiments est expliquée par l’orientation de l’axe d’écoulement principal des eaux entrant dans le barrage, l’écoulement principal étant parallèle à la digue. Par conséquent, le dépôt des sédiments se fait principalement dans la retenue, avant que les eaux de ruissellement n’arrivent au déversoir.

Au niveau du lac de Daimos, en amont du bassin versant, les concentrations en matières solides, mesurées grâce à des prélèvements effectués en 2005 au niveau du déversoir tout au long d’une crue, ont varié entre 0,01 g•L^‑1 et 0,28 g•L^‑1, avec une concentration moyenne de 0,10 g•L^‑1. On peut donc en conclure que la concentration en sédiments des eaux qui sortent du lac de Daimos est nettement supérieure à celle des eaux qui sortent du barrage de Saboun, tout en restant relativement faible.

2.5 Cartographie des unités hydrologiques homogènes

Pour la mise en oeuvre du modèle « Mina », il nous a fallu définir des surfaces de sol à comportement hydrologique homogène, un fonctionnement hydrologique homogène étant défini par un ensemble de paramètres caractéristiques de la surface du sol et agissant sur son comportement hydrodynamique qui règle les conditions d’infiltration et de ruissellement de cette surface. En zone semi-aride méditerranéenne, ces paramètres sont les suivants (EL GAROUANI, 2001; GOMER, 1994; HOUSSA et al., 1998) :

• la nature du sol, par ses caractéristiques texturale et structurale;

• l’occupation du sol qui définit les variations saisonnières de son état de surface; et

• l’état de surface du sol avec la présence ou l’absence de croûtes et d’organisations pelliculaires de surface.

Des campagnes d’échantillonnage des sols et de mesure de ces paramètres sur le terrain ont été réalisées entre 1997 et 1999. Une photographie aérienne (échelle 1:20 000 datant de 1996) a servi de support pour la localisation des parcelles et la spatialisation des paramètres. Les différentes couches d’information ainsi obtenues ont été superposées dans un système d’information géographique (SIG), ce qui nous a permis d’identifier six classes de sols caractérisant le fonctionnement hydrologique des sols du bassin versant de l’Oued Saboun. La répartition spatiale des ces unités hydrologiques a été considérée inchangée dans le temps, au moins pour les deux années d’études, car le parcellaire du bassin est complètement borné et la rotation des cultures comprend deux années de cultures céréalières et une année en jachère (GAY, 2004b; IDRISSI, 2004). Le tableau 3 donne les éléments des différentes couches d’informations retenues dans le SIG et la figure 5 donne le résultat de leur superposition.

Tableau 3

Caractéristiques des principales unités hydrologiques identifiées dans le bassin versant de Saboun.

Characteristics of the principal hydrological units identified in the catchment area of Saboun.

Type de sol	Occupation des sols	Texture	Structure	Croûte de surface	Classes hydrologiques
Peu évolué d’apport alluvial	Sol nu	Argileuse à charge grossière < 40 %	Sub-anguleux peu nette	Structurale	S1
Peu évolué d’apport alluvio-colluvial (terrasse)	Sol nu en jachère	Limoneux-argileuse	Sub-anguleux peu nette	Grossière	S2
Peu évolué d’apport colluvial à caractère vertique	Sol cultivé en jachère	Limoneux-argileuse	Fragmentaire polyédrique très nette	Battance	S3
Vertisol des bas fonds	Sol nu en jachère	Argileux-limoneuse	Fragmentaire polyédrique très nette	Pas de croûte	S4
Peu évolué d’apport colluvial à caractère vertique et calcimagnésique vertique	Sol labouré cultivé orge et fève	Limoneux-argileuse	Massive polyédrique nette	Pas de croûte	S5
Sols minéraux bruts	Affleurement rocheux et habitat	Cailloux et blocs	Grossière	Pas de croûte	S6

Figure 5

Carte des unités hydrologiques homogènes de bassin versant Saboun.

Map of the homogeneous hydrological units in the Saboun watershed.

2.6 Évaluation des paramètres du modèle « Mina »

2.6.1 Caractéristiques topographiques et hydrographiques

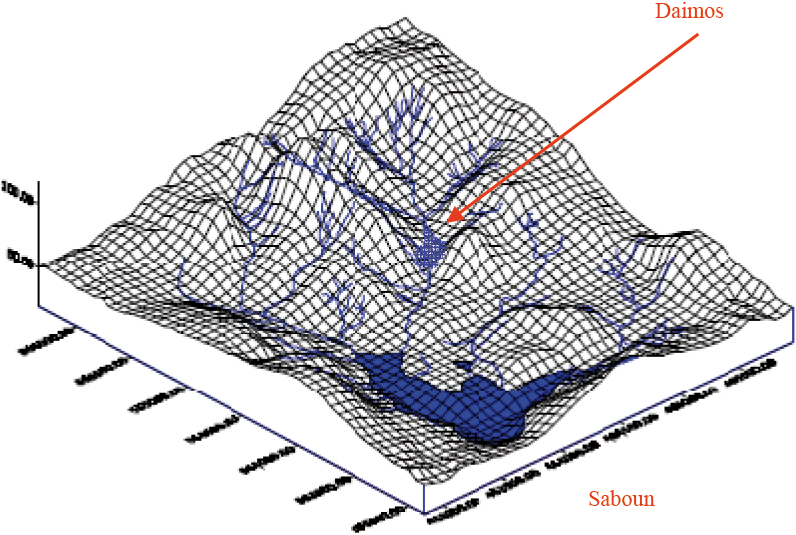
Les données topographiques, extraites de la carte au 1:50 000 d’El Manzla, ont été utilisées pour réaliser un Modèle Numérique de Terrain (MNT) formé de mailles carrées ayant 25 mètres de côté, une altitude étant affectée à chaque maille. Ces données ont été ensuite intégrées dans un Système d’Information Géographique (SIG) pour permettre la détermination des caractéristiques topographiques et hydrographiques du bassin versant, principalement la pente, le sens de l’écoulement superficiel et la taille des impluviums (FAIRFLEID et LEYMARIE, 1991). Le MNT utilisé est présenté sur la figure 6.

Figure 6

Modèle numérique d’altitude de bassin versant Saboun.

Digital elevation model of the Saboun watershed.

En commençant par le point le plus élevé et en suivant les mailles dont l’altitude est la plus faible, il est possible d’établir l’organisation générale du drainage des eaux de ruissellement en tout point du bassin versant et de simuler l’arborescence complète de la circulation des eaux superficielles (GARBRECHT et MARTZ, 1999). Chaque maille possède ainsi un seul sens d’écoulement et une direction d’écoulement vers l’aval qui est celle du gradient d’altitude. La simulation de l’écoulement sur chaque maille est approchée par l’équation de continuité monodimensionnelle de Saint-Venant (onde cinématique), le ruissellement étant calculé par différence entre la hauteur d’eau précipitée et la hauteur d’eau infiltrée.

2.6.2 Modélisation de l’infiltration

En tenant compte du phénomène de battance sur sols marneux, le modèle « Mina » exprime l’infiltration par l’infiltration relative (fr), rapport de la vitesse d’infiltration réelle (f) et de l’intensité de la pluie (Ip). L’infiltration réelle s’exprime en appliquant le modèle d’infiltration de HORTON (1933) en fonction de l’énergie cinétique de BRANDT (1989).

(2)

où fr est le taux d’infiltration relative, f la vitesse d’infiltration en mm•h^‑1, f_∞ la vitesse d’infiltration finale en mm•h^‑1, f₀ la vitesse d’infiltration initiale en mm•h^‑1, w le coefficient de courbature ou de forme, Ec l’énergie cinétique en j•m^‑2.

Selon Gomer et al. (1992) et GOMER (1994), cette méthode permet de décrire de manière très exacte le comportement des sols développés sur un substrat marneux au moyen du modèle de Horton. Dans ces conditions, l’infiltration des sols dépend, d’une part, de l’intensité des précipitations et, d’autre part, de l’humidité initiale qui est représentée dans l’équation 2 par le coefficient de courbature ou de forme (w). La variation (f₀‑ f_∞) est considérée ici comme constante pour chaque unité hydrologique, puisque f₀ et f_∞ sont des paramètres qui sont liés aux caractéristiques du sol, indépendantes de l’humidité initiale dans la modélisation de Horton.

Les données nécessaires à la résolution de cette équation ont été déterminées de façon expérimentale en utilisant les résultats d’expériences de simulation de pluies. Dix tests de simulation de pluies ont été réalisés à raison de un à deux tests par unité hydrologique homogène, en tenant compte de l’étendue spatiale de chacune des unités. L’intensité des précipitations appliquée fut maintenue constante, à une hauteur de 100 mm•h^‑1 pendant une heure. Les données de l’infiltration pour chaque unité de surface ont servi ensuite à l’ajustement des paramètres du modèle de Horton en utilisant la méthode des moindres carrés. Ainsi, on a pu définir, pour chaque unité hydrologique, les vitesses d’infiltration réelle (initiales et finales) et les taux d’infiltration relative (initiale et finale) en divisant par l’intensité de la pluie (100 mm•h^‑1), ainsi que les coefficients de forme (w). Les résultats de ces ajustements sont présentés dans le tableau 4 et la figure 7 donne un exemple graphique d’ajustement.

Tableau 4

Vitesses d’infiltration ajustées par le modèle de Horton, ainsi que l’humidité et le coefficient de forme (w) relatif pour chaque unité hydrologique.

Rates of infiltration, adjusted by the Horton model, as well as moisture and the relative form coefficient (w) for each hydrological unit.

Unité hydrologique	f initiale (fin) (mm•h‑1)	f finale (ffin) (mm•h‑1)	Coefficient de forme w	Humidité initiale vol %	Humidité finale vol %
S1	102	18,7	0,002	31	34
S2	111	8,1	0,116	27	30
S3	103	31,4	0,013	25	33
S4	112	51,3	0,016	24	29
S5	101	5,2	0,011	16	39
S6	102	15,0	0,153	23	27

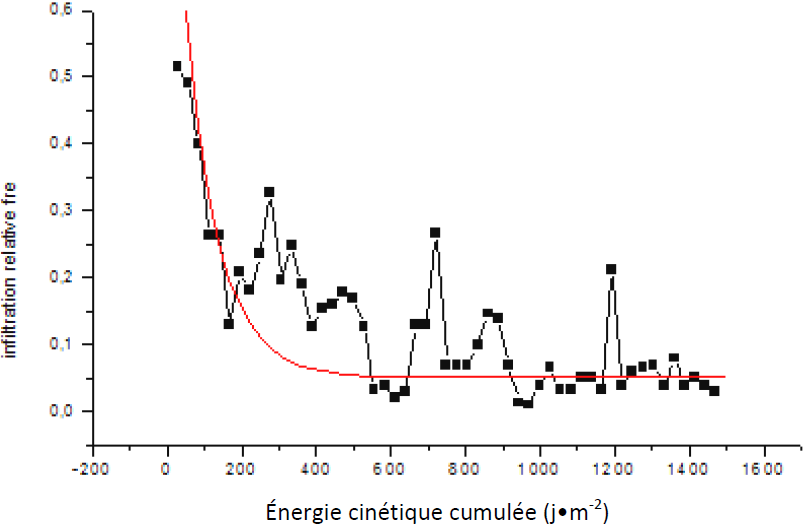
Figure 7

Ajustement des données d’infiltration sous pluie simulée par le modèle de Horton (unité S5).

Adjustment of infiltration data with simulated rain, Horton model (unit  S5).

Les vitesses finales les plus faibles sont enregistrées pour les unités hydrologiques S2 et S5. L’unité S2 représente les surfaces des sols peu évolués d’apport alluvio-colluvial à texture limono-argileuse en présence d’une croûte dure de type grossière, ce qui réduit considérablement l’infiltration du sol. Son infiltration finale (f_∞) est atteinte rapidement (w = 0,116), ce n’est pas le cas de l’unité S5 qui représente les sols cultivés à texture limono-argileuse dont le temps de passage de (f₀) à (f_∞) est très lent (w = 0,011). L’unité S5 regroupe les terrains sur sols à caractère vertique. Elle présente les mêmes caractéristiques pédologiques que l’unité S3, mais l’unité S3 diffère de l’unité S5 par l’existence d’un labour récent sur l’unité S3, ce qui augmente la porosité du sol et accroît très fortement le potentiel d’infiltration du sol.

Pour obtenir les valeurs de l’infiltrabilité initiale pour différents états d’humidité des sols, nous avons utilisé la relation établie par GOMER (1994) pour les sols algériens entre l’infiltrabilité initiale et l’indice d’antériorité des pluies (IK) déterminé selon la formule de KOLHER et LINSLEY (1951) :

(3)

où IK_n est l’indice du jour n exprimé en mm, P_n-1 la pluie du jour n-1 exprimée en mm et α un coefficient de décroissance exponentielle fonction du type de sol et du climat exprimé en jour^-1.

2.6.3 Arrachement des particules

L’arrachement des particules du sol peut être liée à l’action de deux forces de cisaillement : celle liée à l’énergie cinétique des gouttes de pluie lors de leur chute et celle liée à l’énergie cinétique du ruissellement lors de l’écoulement. L’érosion se réalise à condition que ces deux forces dépassent la résistance au cisaillement spécifique du type du sol, appelée aussi énergie cinétique critique de détachabilité des particules. Pour une maille i, de longueur l et de largeur b, le débit solide disponible est exprimé par l’équation suivante (SCHMIDT, 1992) :

(4)

avec :

• I_Qi = ρ_flu Qi Vi

• I_rαi = sin(α) ρ_flu cos (α) r_i l_i b_i V_ri (1-V_g)

• V_ri = 4,506 + 0,615 log (r_i cos(α)).

où Qs est le débit solide (kg•s^‑1), Qi le débit solide pour une maille i (kg•s^‑1), l_i la longueur de la maille i (m), b_i la largeur de la maille i (m), r_i l’ intensité de précipitation (m•s^‑1), IQ_i l’impulsion cinétique de l’écoulement (N•m^‑2), I_rαi l’impulsion cinétique efficace de la pluie (N•m^‑2), m_cr l’impulsion cinétique critique (N•m^‑2), ρ_flu la densité du fluide, V_i la vitesse d’écoulement moyenne (m•s^‑1), V_ri la vitesse moyenne de chute (m•s^‑1), α l’angle de la pente (degrés) et V_g le taux de couverture végétal au sol (%).

En pratique, ces seuils de détachabilité (impulsions cinétiques) sont difficiles à déterminer. Ils le sont par des essais de simulation de pluie sur des parcelles de grande taille, pour des longueurs de 22 m. Les résultats sont ensuite intégrés dans les équations ci-dessus pour le calcul de l’impulsion cinétique critique (m_cr). En l’absence de ce type de simulateur sur le bassin versant de Saboun, les valeurs de l’impulsion cinétique critique de détachabilité pour chaque unité de surface du bassin versant Saboun ont été déduites des valeurs déterminées pour les mêmes types de sols sur le bassin versant de l’Oued Mina (Algérie) et figurant au tableau 5. Les valeurs de l’impulsion cinétique critique de détachabilité sont égales à : 0,0003 pour les sols peu évolués, 0,001 pour les sols très filtrants (vertisols et sols limono-argileux), 0,002 pour les sols argileux à charge grossière et 0,003 pour les bads-lands pierreux.

Tableau 5

Valeurs d’impulsion cinétique critique déterminées pour les sols du bassin versant d’Oued Mina et par analogie pour les surfaces du sol du bassin versant Saboun.

Critical kinetic impulse values for Wadi Mina catchment area soils and, by analogy, for the soil surface of the Saboun catchment.

Type de sol bassin versant Oued Mina (GOMER, 1994)	Type de surface bassin versant Saboun	Impulsion cinétique critique N•m‑2 (d’après GOMER, 1994)
Vertisol très filtrant stable	S4	0,0010
Sol limono-argileux très filtrant	S3, S5	0,0010
Sol rouge très filtrant	-	0,0010
Sol argileux à charge grossière	S2	0,0020
Sol peu évolué	S1	0,0003
Sol argileux salin	-	0,0030
Sol salin très ruisselant	-	0,0030
Sol salin, ruissellant	-	0,0003
Sol argileux salin très ruisselant compact	-	0,0003
Bad-lands peu pierreuses	-	0,0001
Bad-lands pierreuses	S6	0,0030

2.6.4 Transfert des débits liquides et solides jusqu’à l’exutoire

Le routage et le transfert des eaux entre les mailles sont basés sur l’équation de continuité monodimensionnelle appelée aussi deuxième équation de Saint-Venant.

Pour distinguer entre un écoulement en nappe et un écoulement concentré en chenaux, nous avons utilisé la notion de surface limite d’apparition des rigoles. Sur les marnes tertiaires du bassin versant de l’Oued Mina, cette surface est évaluée à 1 000 m² au moyen d’un Système d’Information Géographique par confrontation de la carte des aires contributives à la carte du réseau de drainage (GOMER et al., 1992). Dans le bassin versant de l’Oued Saboun, sur les marnes du Miocène, elle a été évaluée par la même méthode à 1 200 m² qui correspond à une longueur de la pente comprise entre 30 et 40 m à partir de la ligne de partage des eaux.

Le transfert des particules solides, par analogie avec l’équation de continuité pour le transfert de la phase liquide, se fait de la même manière en appliquant l’équation de continuité adaptée à la phase solide. Les dépôts et les reprises sont gérés par le calcul d’un bilan entre la sédimentation et l’érosion, fonction du coefficient de dépôt C_dep qui varie entre 0 (dépôt) et 1 (érosion). Ce coefficient de dépôt est calculé comme suit :

(5)

où h est la hauteur de la lame d’eau, ω la vitesse de sédimentation, ∆x la distance et v la vitesse de flux liquide.

3. Résultats et discussions

Le modèle « Mina » a été appliqué pour toutes les averses enregistrées à la station Saboun au cours des deux années hydrologiques 1997-98 et 1998-99. Nous avons choisi ces deux années hydrologiques parce qu’elles permettent de bien encadrer le régime hydrologique du bassin versant de l’Oued Saboun. En prenant les deux stations de Tanger DPE et Kalaya comme stations de référence, avec une hauteur pluviométrique annuelle de 797 mm, l’année 97-98 présente une période de retour de trois ans humides, alors que l’année 98-99, pour une hauteur pluviométrique annuelle de 444 mm, présente une période de retour de vingt ans secs.

La simulation des débits liquide et solide a été réalisée au pas de temps de 5 min, identique au pas de temps d’enregistrement des hauteurs d’eau du lac par le limnigraphe. Quant aux caractéristiques topographiques et pédologiques, elles ont été définies pour chaque maille carrée de 25 m de côté par l’utilisation d’un SIG intégrant le MNT et la carte pédologique du bassin versant.

Le modèle est appliqué de façon distincte sur les parties amont et aval du bassin versant :

• la partie amont correspond au bassin versant de Daimos d’une superficie de 228 ha;

• la partie aval correspond au bassin versant de Saboun sans le bassin versant de Daimos, sa superficie est de 574 ha.

Cette désagrégation du bassin versant de l’Oued Saboun en deux parties imbriquées est appliquée de manière à introduire une fonction de stockage de l’eau et des sédiments dans le lac de Daimos. Ne disposant pas de mesures hydrométriques à Daimos, nous sommes partis sur l’hypothèse que le lac était vide en début de simulation (1^er octobre 1997), qu’il se remplit à chaque crue et déverse à partir d’un volume de 30 000 m³. Le niveau de remplissage de la retenue de Daimos avant l’averse tient compte de son niveau de remplissage à la fin de l’averse précédente et de l’évaporation de l’eau stockée depuis l’averse précédente. Nous avons calculé le volume journalier évaporé sur le lac de Daimos en multipliant l’évaporation journalière mesurée au bac Colorado enterré près du barrage de Saboun par la surface du plan d’eau au barrage Daimos le même jour. Pour les lacs collinaires de la zone semi-aride, l’évaporation mesurée au bac Colorado enterré est en effet peu différente de l’évaporation du lac (GAY, 2004a). L’infiltration dans la retenue de Daimos a été négligée.

La figure 8 compare les crues entrant dans les lacs de Saboun et Daimos à la date du 03/02/1998 et la figure 9 montre la reconstitution, par le modèle « Mina », des débits entrant dans le barrage de Saboun avant et après calibration du paramètre d’infiltrabilité initiale pour l’événement du 18/12/1997.

Figure 8

Crue du 03/02/1998 (en violet, le débits simulés sortant du lac Daimos ; en rouge les débits reconstitués entrant au barrage Saboun)

Flood of 03/02/1998 (in purple, simulated flows leaving lake Daimos; in red, reconstituted flows entering the Saboun reservoir).

Figure 9

Comparaison des débits observés et simulés entrant au barrage Saboun pour la crue du 18/12/1997, avant et après calibrage.

Comparison of observed and simulated flows entering Saboun reservoir for the flood of 18/12/1997, before and after calibration.

La figure 10 présente les écarts entre les volumes observés et les volumes simulés pour l’ensemble des crues en fonction de l’indice d’antériorité des pluies (IK) avant calibration et après calibration du paramètre d’infiltrabilité. Le tableau 6 présente les résultats de cette calibration en matière de volume d’eau entrant au barrage et d’envasement de la retenue en fonction des volumes de sédiments déversés.

Figure 10

Comparaison entre les volumes des crues simulées et observées en fonction de l’indice IK avant et après correction d’infiltrabilité.

Comparison between volumes of simulated and observed flows according to index IK, before and after correction of the permeability.

Tableau 6

Apports en eau et en sédiment simulés crue par crue à l’exutoire du barrage Saboun entre 1997 et 1999.

Water and sediment fluxes, simulated for individual flood events, at the Saboun dam outlet between 1997 and 1999.

Date	Pr (mm)	I5 max mm•h‑1	IK	Volumes ruisselés mesurés (m3)	Volumes déversés mesurés (m3)	Volumes ruisselés simulés (m3)	Sédiments simulés (kg)	Sédiments déversés estimés (kg)	Volume d’envasement de la retenue, estimé (m3)	Masse d’envasement de la retenue estimé (kg)
07/11/97	15,5	21	0	9 382	0	3 974	968 418	0	745	968 418
18/11/97	18,5	66	0	4 149	0	4 866	1 358 708	0	1 045	1 358 708
21/11/97	37,5	48	20	65 333	0	3 482	699 049	0	538	699 049
24/11/97	16	30	13	11 770	0	2 683	654 732	0	504	654 732
25/11/97	31,5	24	15	18 152	0	3 812	1 294 247	0	996	1 294 247
4‑5/12/97	47	36	34	239 694	146 830	114 278	4 344 404	8 810	3 322	4 318 600
16/12/97	39	48	2	16 504	1 720	9 111	2 746 957	103	2 113	2 746 900
17‑18/12/97	82,5	78	36	181 453	82 615	121 307	3 111 806	4 957	2 382	3 096 600
19/12/97	5	24	43	12 848	64 860	3 326	445 431	3 892	334	434 200
22/12/97	24	36	23	68 450	32 354	56 372	1 836 060	1 941	1 408	1 830 400
12/01/98	24,5	36	36	43 340	17 194	35 804	1 313 880	1 032	1 008	1 310 400
01/02/98	11,5	20	24	22 061	16 084	7 083	126 571	965	95	123 500
3‑4/2/98	70	49	40	251 731	234 486	97 760	2 839 833	14 069	2 152	2 797 600
06/02/98	12	14	20	68 732	55 805	42 061	1 229 083	3 348	938	1 219 400
26/09/98	60	84	6	13 850	0	204 570	11 171 031	0	8 593	11 171 031
29‑31/12/98	65	54	0	11 106	0	7 882	860 497	0	662	860 497
12/01/99	36,5	30	14	3 824	0	11 410	3 498 475	0	2 691	3 498 475
17/01/99	17,5	18	5	4 109	0	9 456	315 626	0	243	315 626
21/01/99	23	12	0	4 480	0	4 442	569 262	0	438	569 262
23/01/99	20,5	12	5	9 188	0	3 844	498 370	0	383	498 370
24‑25/02/99	25	30	37	11 180	0	7 277	725 631	0	558	725 631
28/02/99	10	12	4	1 202	0	1 642	177 561	0	137	177 561
24/03/99	53	78	5	24 218	0	6 626	642 575	0	494	642 575
01/05/99	14	12	1	3 895	0	2 637	263 470	0	203	263 470

Pr : précipitation ; I5 : intensité maximale de pluie en 5 min ; IK : indice d’humidité de Kolhler.

La confrontation des résultats simulés et observés montre que le modèle sous-estime l’écoulement pour les averses à fort indice d’humidité des sols et surestime l’écoulement pour les averses isolées à indice d’humidité faible, proche de 0. Ceci est expliqué par la complexité des processus qui génèrent le ruissellement sur les sols du bassin versant de Saboun. Pour les sols à texture limono-argileuse du bassin versant de Saboun, comme les unités S2, S3 et S5, le modèle de Horton peut être appliqué sans inconvénient car les simulations de pluies ont révélé que ce type de sol possédait les taux les plus faibles d’infiltration avec des coefficients de ruissellement atteignant 70 %. En effet, l’aptitude au ruissellement des sols à texture limono-argileuse est liée principalement à la dégradation structurale de la surface du sol sous l’action de la pluie et à la formation de la croûte de battance. Cependant, le caractère vertique de certains sols (unités S3 et S5) accroît leur capacité à l’infiltration lorsque les sols sont secs, en raison de l’existence de fentes de retrait plus ou moins larges et profondes selon l’humidité du sol. Pour les vertisols, stables et filtrants (unité S4), ils se comportent en début de saison des pluies comme des réservoirs ayant une certaine capacité de stockage, leur capacité au ruissellement dépend donc de leur teneur en eau et non de la formation de la battance. Pour une averse qui survient dans des conditions antérieures d’humidité faible sur un sol argileux, les fentes et fissures entraînent une importante infiltration de la pluie dans le sol avant le ruissellement (GERMANN, 1990; MRABET, 1989), favorisant beaucoup plus des écoulements hypodermiques que des écoulements de surface directs sur les versants. Ce phénomène a été également observé par Heusch (1970) sur le bassin versant de Mda (région de Ouezzane) sur le même type de sol (sol marneux) du Rif occidental. Il a constaté que plus de 70 % des eaux écoulées sur les versants, rejoignent les talwegs par des écoulements hypodermiques liés principalement à la fissuration. Ces écoulements sont plus importants en année sèche qu’en année humide.

Le caractère plus ou moins argileux et vertique des sols du bassin versant de l’Oued Saboun provoque donc une sous-estimation de l’infiltration pour les averses isolées dont l’indice des pluies antérieures est faible (IK proche de 0). Par contre, pour une averse qui survient dans des conditions d’humidité des sols importante (IK supérieur à 15 mm), le sol très humide perd la cohésion de ses particules. Il s’ensuit un effondrement de la structure macroscopique et la disparition d’une partie des pores assurant l’infiltration et la rétention d’eau. L’espace poral ou intergranulaire n’est plus interconnecté, ce qui entraîne une réduction de l’infiltration et sa surestimation par le modèle de Horton.

En matière d’érosion, les résultats de la simulation du transport solide ont été comparés aux données de l’envasement issues de la bathymétrie. L’envasement calculé par le modèle est estimé à 22 850 tonnes pour l’année 1997-1998 et 18 700 tonnes pour l’année 1998-1999, alors que la moyenne interannuelle estimée par bathymétrie sur la période 1999-2004 est de 27 750 tonnes. Si on tient compte des précipitations des années 2001-2002 et 2003-2004, exceptionnellement humides et dépassant 1 000 mm, l’érosion semble être correctement simulée par le modèle « Mina ». Les résultats de cette comparaison montrent donc que la transposition sur le bassin versant de l’Oued Saboun des impulsions cinétiques critiques déterminées sur les sols du bassin versant de l’Oued Mina pour les mêmes types de sols expriment bien les processus érosifs sur le bassin versant de l’Oued Saboun.

À partir de ces résultats de simulation, nous avons cherché à reconstituer le remplissage et l’envasement du barrage à l’échelle mensuelle sur la période comprise entre septembre 1997 et août 1999. Les apports mensuels en eau au barrage sont calculés en sommant les volumes des crues; l’envasement mensuel est calculé en sommant les volumes du transport solide simulé dont on soustrait la part des sédiments sortant par le déversoir. Nous divisons le tonnage simulé par la densité moyenne mesurée de sédiment (dmoy = 1,3) pour obtenir le volume sédimenté dans le barrage. La part des sédiments déversés est obtenue par le produit du volume déversé et de la concentration moyenne en matières solides des déversements. Les sorties en eau du barrage sont, d’une part, l’évaporation et, d’autre part, l’utilisation de l’eau du lac pour l’alimentation du périmètre irrigué. L’évaporation est calculée à l’échelle journalière à partir des mesures au bac Colorado enterré près de la digue du barrage et l’utilisation de l’eau pour l’irrigation est calculée à partir de la consommation électrique de la station de pompage. Les volumes mensuels utilisés, prélevés dans le lac de Saboun, sont consignés au tableau 7.

Tableau 7

Utilisation mensuelle de eau du barrage Saboun en m³.

Monthly use of water from the Saboun reservoir in m³.

	Sept	Oct	Nov	Déc.	Janv.	Fév.	Mars	Avril	Mai	Juin	Juillet	Août
Année pluvieuse 1997/1998	0	0	0	0	0	0	0	0	7 300	18 100	8 200	15 000
Année sèche 1998/1999	14 300	7 500	8 200	6 700	5 000	3 600	9 800	14 600	9 900	11 000	35 000	65 000

Les résultats de cette reconstitution sont présentés à la figure 11. Ils montrent une bonne corrélation entre les données de remplissage mesurées et simulées au barrage de Saboun. En ce qui concerne l’envasement, le contrôle bathymétrique effectué dans le lac en octobre 1998 correspond assez bien à l’envasement déterminé par simulation à la même date. En outre, la simulation montre que les apports en sédiments ont eu lieu principalement au cours de la période hivernale de décembre 1997 à février 1998.

Figure 11

Variation de l’état de remplissage du barrage Saboun de novembre 1997 à octobre 1999 : (comparaison entre les données simulées en rouge et les données mesurées en bleu).

Variation of the state of filling of the Saboun’s dam from November 1997 to October 1999: (comparison of simulated data, in red and measured data, in blue).

4. Conclusion

Cette étude avait pour objectif de simuler les apports en eaux et en sédiments au barrage collinaire de l’Oued Saboun en utilisant le modèle « Mina », modèle hydrologique distribué à base physique basé sur l’équation d’infiltration de Horton pour le calcul de l’écoulement et de l’énergie cinétique critique de détachabilité des particules du sol pour le calcul de l’érosion.

La confrontation des résultats aux données observées a montré, pour un calage des paramètres d’infiltration basé sur des expériences de simulation de pluies effectuées au printemps (mars et avril 1999), une nette surestimation des volumes écoulés simulés en début de saison des pluies, pour de faibles indices d’antériorité des pluies correspondant à des sols secs. Cet écart peut être atténué par la prise en compte de la présence de fissures dans les sols marneux en augmentant le taux d’infiltration initial dans l’équation d’infiltration de Horton. Inversement, la confrontation des résultats aux données observées a montré une nette sous-estimation des volumes écoulés simulés pour les forts indices d’antériorité des pluies correspondant à des sols très humectés. Cet écart peut être atténué par une réduction du taux d’infiltration final dans l’équation de Horton. Ces améliorations ont permis une meilleure adaptation du modèle « Mina » au comportement hydrodynamique des sols du bassin versant de l’Oued Saboun.

Pour améliorer la qualité des ajustements de l’équation de Horton aux sols argileux et limono-argileux vertiques, il semble donc nécessaire de développer des expériences de simulation de pluies à différentes périodes de l’année en tenant compte des caractéristiques hydriques initiales des sols qui déterminent leurs capacités à l’infiltration. La prise en compte d’une évolution saisonnière de cette capacité d’infiltration, en relation avec l’humidité du sol, semble indispensable pour rendre compte de manière satisfaisante du fonctionnement hydrologique du bassin versant de l’Oued Saboun et probablement de tous les bassins versants du sud de la Méditerranée qui possèdent les mêmes types de sols.