Abstracts
Résumé
Cet article analyse la contribution de la macroéconomie des défauts de coordination au chômage d’équilibre. La littérature consacrée aux défauts de coordination souligne les manifestations de l’interaction entre agents rationnels dans des économies décentralisées. Une telle aproche offre des fondements microéconomiques à l’existence du chômage d’équilibre persistant dans un cadre d’équilibre général sans présupposer la rigidité des prix et des salaires. Les modèles de chômage d’équilibre peuvent être regroupés en trois catégories selon les causes attribuées aux défauts de coordination. Les thèmes développés sont (i) les fondements microéconomiques des défauts de coordination, (ii) les externalités de demande agrégée, (iii) les externalités d’échanges et (iv) les externalités dues aux rendements croissants. La politique économique et la sélection des équilibres sont également développées dans cet article.
Abstract
This article analyzes the contribution of the macroeconomics of coordination failures to unemployment equilibrium theory. Coordination failures deal with the interactions of rational agents in decentralized market economies. Such an approach gives microeconomic foundations for persistent unemployment equilibria in a general equilibrium framework without assuming sticky prices and wages. In this recent literature, we distinguish between three kinds of coordination failures, each of which causes unemployment. The issues are then: (i) the microeconomics of coordination failures, (ii) the aggregate demand externalities, (iii) the transaction externalities and (iv) the role of increasing returns to scale. Policies and equilibrium selection are developed within the article.
Article body
Introduction
La macroéconomie du chômage d’équilibre s’est récemment renouvelée avec la littérature des défauts de coordination. Une telle approche permet de démontrer l’existence d’équilibres de sous-emploi ordonnés en termes de bien-être dans des économies concurrentielles en régime de prix et salaires flexibles. L’inefficacité de tels équilibres assigne alors un rôle à la politique économique dans la sélection d’un équilibre haut. Le point remarquable de cette approche est qu’elle rend généralement possible le sous-emploi des ressources dans un cadre d’équilibre général sans recourir à une explication en termes de rigidité des prix. Traditionnellement, l’équilibre général concurrentiel explique les situations de sous-emploi par le fait que les prix relatifs sont faux. L’existence de chômage involontaire est alors généralement attribuée soit à la lenteur du processus d’ajustement des prix (Patinkin, 1956), soit à la rigidité des prix (Bénassy, 1993). La littérature théorique consacrée au chômage éprouve ainsi certaines difficultés à rendre compte de l’existence du chômage persistant dans un cadre d’équilibre général à prix et salaires flexibles.
La littérature sur le chômage d’équilibre met en exergue deux types de problèmes. Le premier a trait aux modèles d’équilibre général qui fondent l’existence de chômage involontaire sur les rigidités de prix et de salaires (Drèze, 1975, 1997; Ball et Romer, 1991; Bénassy, 1993). Comme l’a souligné Patinkin (1956), le chômage (involontaire) est incompatible avec l’équilibre général concurrentiel. À défaut d’une théorie générale de la coordination en concurrence imparfaite, cette situation a justifié le recours à une approche en équilibre partiel. Le deuxième problème concerne précisément l’équilibre partiel. Trois approches sont adoptées dans la littérature. La théorie des contrats optimaux (Baily, 1974; Gordon, 1974; Azariadis, 1983) introduit l’incertitude sur le marché du travail. Ces travaux déterminent en fait les conditions dans lesquelles les salaires sont rigides et le chômage efficient. Les théories du salaire d’efficience (Shapiro et Stiglitz, 1984; Weiss, 1991) qui s’intéressent à l’imperfection de l’information sur le marché du travail démontrent l’existence du chômage involontaire d’équilibre et donnent des fondements microéconomiques à la rigidité des salaires réels. Cependant, la rigidité des salaires et la centralisation des échanges sur le marché du travail limitent l’intérêt d’une telle approche. D’autres approches s’intéressent plus spécifiquement à la décentralisation sur le marché du travail. Ainsi, les théories de l’appariement (Pissarides, 2000) ou de la prospection (Diamond, 1981; Mortensen, 1986) traitent du chômage d’équilibre comme un phénomène propre au seul marché du travail. Dans ces deux perspectives proches, l’échange sur le marché du travail est une activité décentralisée. Les entreprises et les consommateurs font face à des frictions (délais d’ajustement, information imparfaite) et supportent des coûts de transactions avant de se rencontrer. L’intérêt de ces modèles est de montrer que l’activité de recherche d’emploi et le rationnement ne sont pas équivalents dans la mesure où un agent peut être rationné sur un marché du travail et rechercher par ailleurs activement un autre emploi. L’existence de frictions ou de coûts de transaction dans l’activité d’échange ne concernent pas uniquement le seul marché du travail dans la mesure où la manifestation d’un rationnement invoque une analyse qui prend en compte les interdépendances générales entre marchés ou secteurs. Le chômage est un phénomène complexe dont l’explication ne peut se limiter au seul marché du travail et qui requiert de distinguer l’activité de recherche d’emploi de la manifestation du rationnement. La macroéconomie des échecs de coordination propose des modèles qui tentent de surmonter ces deux difficultés.
La théorie des défauts de coordination analyse les manifestations et les conséquences de l’interaction entre agents rationnels dans des économies décentralisées. Ainsi, l’éviction de la chambre de compensation walrasienne, inhérente à la coordination centralisée, constitue le point de départ de cette littérature. La décentralisation se manifeste par la présence d’externalités dans les échanges, dans la production ou dans la consommation. La prise en considération des modalités d’organisation et de réalisation des transactions permet de souligner les manifestations de la décentralisation et d’analyser ses conséquences sur la détermination du niveau de l’activité et de l’emploi d’équilibre. De cette manière, l’approche des échecs de coordination rend compatible l’existence du chômage d’équilibre avec une analyse en termes d’équilibre général. Cependant, la diversité des modèles atteste du fait qu’il s’agit d’une littérature vaste au sein de laquelle une classification s’impose. Nous excluons d’emblée de cet article les modèles à prix fixes (Ball et Romer, 1991; Drèze, 1997) pour la raison précédemment invoquée. Dans cette perspective, on distingue dans la littérature trois types de défauts de coordination appliqués à la théorie du chômage. Ainsi, les échecs de coordination peuvent être fondés sur des externalités de demande agrégée qui se manifestent lorsque le mode de concurrence est imparfait. Ensuite, les défauts de coordination peuvent reposer sur des externalités dans les échanges. Enfin, les externalités dues aux rendements croissants peuvent engendrer des équilibres inefficaces ordonnés. Dans tous les cas, le système concurrentiel de marché est mis en défaut ce qui nécessite la mise en place de politiques économiques dont quelques exemples sont donnés.
Cet article s’articulera autour de quatre thèmes. Une première section est consacrée aux fondements microéconomiques du concept de défauts de coordination. Une deuxième section analyse les externalités de demande agrégée. Le cadre de référence est celui de la concurrence imparfaite. Une troisième section est consacrée aux externalités de transaction. L’approche par les coûts de transaction sera privilégiée. Une quatrième section a trait à la relation entre les rendements croissants et le sous-emploi d’équilibre. Des applications de politiques économiques sont étudiées. Dans chacun des cas nous proposons un modèle stylisé qui constitue une version simplifiée d’un modèle représentatif de la littérature. Nous soulignerons aussi les intérêts et les limites de tels modèles et comparerons les différentes approches. On s’attachera notamment à montrer, qu’au-delà de leur spécificité, les modèles présentés dans chacune des approches comportent des caractéristiques communes.
1. Fondements microéconomiques des défauts de coordination
L’approche des défauts de coordination est systématisée par Cooper et John (1988) dans le cadre d’analyse des jeux de coordination. Plus récemment, Cooper (1999) donne des applications possibles à la macroéconomie pour de tels jeux. Dans ce contexte, il est possible de proposer des fondements microéconomiques aux échecs de coordination. Avant de définir de manière précise le concept de défauts de coordination et d’étudier les conditions nécessaires et suffisantes de leur existence, donnons un exemple.
1.1 Un exemple
Considérons à titre d’illustration l’histoire suivante. Imaginons une économie composée de deux firmes notées respectivement A et B qui doivent décider si elles ont intérêt à employer davantage afin d’accroître leur capacité de production et leurs ventes. Chaque entreprise a ainsi le choix entre deux actions : embaucher de nouveaux salariés (E) ou ne pas les embaucher (NE). Si une entreprise décide d’employer davantage, elle aura un gain qui variera selon le jeu considéré. Chaque firme effectue son choix en prenant la stratégie de l’autre firme comme donnée. Les stratégies et les gains de chaque firme sont représentés dans les deux jeux statiques suivants écrits sous forme normale. Les vecteurs lignes sont les gains (la première composante indique le profit de la firme A et la seconde celui de la firme B).
Jeux I : défaut de coopération
Jeux II : défaut de coordination
Le jeu I de gauche est un jeu de type dilemme du prisonnier. L’élimination des stratégies dominées aboutit à la situation (NE,NE) qui est un équilibre de Nash non coopératif notamment dominé par l’état (E,E) qui n’est pas un équilibre. L’inefficacité est alors une conséquence de l’absence de coopération. Afin de remédier à une telle inefficacité, le mode de comportement des firmes ou les règles du jeu doivent être modifiées, voire le jeu répété. Le jeu II de droite présente une toute autre situation[1]. Il n’existe pas de façon naturelle de jouer le jeu. Un tel jeu possède deux équilibres de Nash non coopératifs[2] (E,E) et (NE,NE). Il est évident que (E,E) est associé à un niveau de bien-être supérieur à l’autre équilibre. À la différence du cas précédent, l’état (E,E) est un équilibre (associé à un plus haut niveau d’emploi que l’état (NE,NE)). Si l’économie demeure en (NE,NE), alors aucune firme n’a intérêt à dévier. Dans ce cas, le chômage est persistant. Un changement général de stratégie des agents se traduisant par un effort coordonné des deux entreprises améliorerait cependant le bien-être et pourrait conduire l’économie en (E,E). Cependant, aucune firme prise individuellement n’a d’incitation à dévier étant donné que leurs décisions ne sont pas coordonnées. La possibilité d’équilibres multiples Pareto ordonnés provient de l’incapacité des agents à coordonner leurs choix. Dans ce cas, l’économie reste bloquée à un équilibre inférieur. Une économie présente donc un défaut de coordination lorsque les agents se coordonnent sur un équilibre inefficace alors qu’existent d’autres équilibres de qualité supérieure. Plusieurs propriétés expliquent la présence de défauts de coordination.
1.2 Défauts de coordination, complémentarités stratégiques et effets de report
Les propriétés des échecs de coordination sont données dans l’article de Cooper et John (1988). On propose ici une version simplifiée à deux agents qui généralise l’exemple précédent. Considérons une économie composée de deux firmes notées A et B. Chaque firme doit choisir une stratégie z (une action représentant un niveau d’emploi), où z ∈(0, 1). Lorsque la firme A choisit l’action zA alors sa fonction de gain s’écrit ∏A(zA, zB), où ∏A est le gain de la firme A et zB l’action de la firme B. Il est supposé que la fonction de gains est continue et différentiable deux fois, croissante et concave. On a donc ∂∏A / ∂zA > 0 et ∂2∏A / ∂z2A < 0. On suppose aussi que ∂∏A / ∂zA(0, 0) > 0 et ∂∏A / ∂zA(1, 1) < 1. Ainsi, si la firme B choisit un effort extrême (nul ou unitaire), alors la firme A a intérêt à choisir un effort intérieur. La même analyse s’applique pour la firme B. L’hypothèse importante est que le profit de la firme A ne dépend pas seulement de ses choix mais aussi des choix effectués par la firme B. Dans ce cas, les choix de la firme B, qui se comporte aussi de manière stratégique, a des effets sur le gain de la firme A (ici ∂∏A / ∂zB ≠ 0). Cette hypothèse est vraie pour chaque entreprise. Ainsi, le choix de chaque firme influence non seulement son gain et sa stratégie mais aussi les gains et les stratégies de l’autre firme ce qui traduit la présence d’externalités. Lorsque les firmes ne coopèrent pas, de telles externalités ne sont pas internalisées. La présence de telles externalités traduit l’existence d’effets de report et de complémentarités stratégiques.
Si ∂∏A / ∂zB > 0 et ∂∏B / ∂zA > 0, alors l’économie comprend des effets de reportpositifs. Si ∂∏A / ∂zB < 0 et ∂∏B / ∂zA < 0, alors l’économie comprend des effets de report négatifs. Il existe des effets de report positifs (négatifs) lorsqu’un accroissement d’effort d’un agent induit un bénéfice (une perte) pour l’autre agent. Le tableau de droite de l’exemple précédent illustre la présence d’effets de report dans la mesure où le gain de chaque entreprise est une fonction croissante d’un changement de stratégie à la hausse de l’autre entreprise. Ainsi, à l’équilibre bas, le gain de la firme A augmente lorsque la firme B décide d’employer d’avantage (il passe de 2 à 3). Le même raisonnement vaut pour la firme B. L’effet de report mesure l’effet d’un changement de stratégie d’un agent sur le gain d’un autre pour une action donnée de l’agent dont on mesure le gain. Les effets de report mesurent donc les interactions entre firmes dans l’espace des gains.
Si ∂2∏A / ∂zA ∂zB > 0 et ∂2∏B / ∂zB ∂zA > 0, alors le jeu comprend des complémentarités stratégiques[3]. Si par contre ∂2∏A / ∂zA ∂zB < 0 et ∂2∏B / ∂zB ∂zA < 0, alors le jeu comprend des substituabilités stratégiques. Il existe des complémentarités stratégiques (substituabilités stratégiques) lorsqu’un changement de stratégie d’un agent à la hausse accroît (diminue) le bénéfice marginal de l’autre agent. Dans le jeu II de l’exemple précédent, l’accroissement de gain de la firme B qui passe de la stratégie NE à la stratégie E est de –2 lorsque la firme A choisit la stratégie NE alors qu’il est de 1 lorsque la firme A choisit la stratégie E, avec E > NE (et symétriquement pour A). Ainsi, l’accroissement de gain de la firme B, consécutivement à un changement de stratégie, augmente lorsque la firme A sélectionne un choix lui procurant un gain plus élevé. Une complémentarité stratégique mesure ainsi le changement de gain relatif à un changement de stratégie d’un agent comme une fonction croissante de la stratégie d’un autre. Les complémentarités stratégiques relèvent donc des interactions dans l’espace des stratégies.
La stratégie optimale pour la firme A est ϕ(zB), où ϕ est la fonction de réaction de la firme A (φ(zA) pour la firme B) lorsque la firme B a pour stratégie zB (lorsque la firme A joue zA). Un équilibre non coopératif est un couple de stratégies (ẑA, ẑB) tel que ẑA = ϕ(ẑB) et ẑB = φ(ẑA) . Soit E = {(ẑA, ẑB) ∈[0, 1] ∞ [0, 1] ⋀ ∏′A(ϕ(zB), zB) = 0 et ∏′B(φ(zA), zA) = 0} l’ensemble des équilibres de Nash. Afin d’étudier les propriétés d’inefficacité de tels équilibres, il est utile de définir les équilibres coopératifs de ce jeu. Un équilibre coopératif est une stratégie z ∈[0, 1] choisie par un planificateur qui détermine la stratégie optimale, en se limitant au cas où les deux entreprises ont les mêmes stratégies. À la différence du contexte non coopératif, le planificateur tient compte de l’influence de la stratégie de la firme A sur le choix de la firme B. Le planificateur choisit donc la stratégie commune pour chaque firme, notée z, qui permet de maximiser la fonction de gains ∏(z, z). Soit Ẽ = {z ∈[0, 1] ⋀ ∂∏A / ∂zA(z, z) + ∂∏A / ∂zB(z, z) = 0} l’ensemble des équilibres coopératifs. Quatre propositions significatives caractérisent les propriétés de cette économie.
Proposition 1.1Les complémentarités stratégiques constituent une condition nécessaire à l’existence d’équilibres multiples.[4]
Preuve. Considérons la firme A. La fonction de réaction de la firme A est ϕ(zB). Celle-ci donne la meilleure réponse à un changement des choix de l’autre firme dans le plan (zA, zB). Le choix optimal de la firme A vérifie la condition d’optimalité ∂∏A / ∂zA(ϕ(zB), zB) = 0. Si la fonction de réaction est croissante sur un intervalle donné, de multiples intersections sont possibles avec la fonction de réaction de l’autre agent comme l’indique le graphique 1. La différentiation de la condition d’optimalité précédente permet de calculer la pente η de la fonction de réaction de la firme A. Ainsi (∂2∏A / ∂z2A) dzA + (∂2∏A / ∂zA ∂zB) dzB) = 0 donne η = – (∂2∏A / ∂zA ∂zB) / (∂2∏A / ∂z2A), où η = dzA / dzB. En raison de la concavité de ∏A, le signe de η va dépendre de la présence de complémentarités ou de substituabilités stratégiques, soit sign η = sign∈(∂2∏A / ∂zA ∂zB). En présence de complémentarités stratégiques ∂2∏A / ∂zA ∂zB > 0 soit η > 0. La fonction de réaction de la firme A est alors croissante. Dans l’autre cas (η < 0), la fonction de réaction est décroissante.
Proposition 1.2Si le jeu possède des effets de report, alors les équilibres non coopératifs sont inefficaces.
Preuve. Soit ẑ la stratégie de chaque firme à l’équilibre non coopératif. Par définition, on a ∂∏A / ∂zA(ẑ, ẑ) = 0. Si le jeu possède des externalités positives, alors ∂∏A / ∂zA(ẑ, ẑ) > 0 soit ∂∏A / ∂zA(ẑ, ẑ) + ∂∏A / ∂zB(ẑ, ẑ) > 0, ce qui montre que ẑ n’est pas un équilibre coopératif. Cet équilibre est donc inefficace.
Proposition 1.3Si les effets de report sont positifs, alors les équilibres non coopératifs de Nash peuvent être ordonnés au sens de Pareto.
Preuve. Soit d∏A(ϕ(ẑ), ẑ) / dẑ = (∂∏A / ∂zA(ẑ, ẑ)) . dϕ(ẑ) / dẑ + ∂∏A / ∂z(ϕ(ẑ), ẑ) la différentielle totale de ∏A en (ẑ, ẑ). Comme dϕ(ẑ) / dẑ = 0 alors d∏A(ϕ(ẑ), ẑ) / dẑ = ∂∏A / ∂z(ϕ(ẑ), ẑ) > 0. Ainsi, le gain de la firme A, évalué le long de sa fonction de réaction, s’accroît lorsque l’effort stratégique de la firme B augmente. Les équilibres non coopératifs avec effort stratégique élevé sont préférés à ceux où l’effort est moindre. Les reports positifs améliorent donc le bien-être.
Proposition 1.4Si la réponse agrégée consécutive à un choc l’emporte sur la réponse d’un agent pris isolément, alors il existe des effets multiplicateurs.
Preuve. On suppose ici que la fonction de gain de chaque firme s’écrit ∏j(zA, zB, θ), j = A, B. Le paramètre θ est le même pour les deux firmes. On suppose aussi que ∂2∏A / ∂zA ∂θ∈> 0 (l’effort marginal augmente avec θ). L’analyse vaut pour la firme B. L’effort agrégé l’emporte donc sur l’effort individuel lorsqu’un choc affecte tous les agents[5], ici ∂(ẑA + ẑB) / ∂θ > ∂ẑA / ∂θ. De tels effets peuvent être interprétés comme une illustration du concept keynésien[6].
Finalement, la possibilité d’équilibres multiples (de Nash) ordonnés en termes de bien-être provient de l’incapacité des agents à coordonner leurs choix[7]. La multiplicité d’équilibres est due à des complémentarités stratégiques suffisamment fortes. La possibilité d’un ordonnancement local de tels équilibres ressort de la présence d’effets de report de même signe qui constituent donc une condition suffisante à l’existence d’échecs de coordination. Le graphique 1 illustre cette idée.
Graphique 1
Multiplicité d’équilibres et défauts de coordination
Les deux courbes sont les fonctions de réaction des deux firmes A et B. Les courbes d’isoprofit font apparaître la direction dans laquelle le profit s’accroît. L’hypothèse d’effets de reports positifs s’interprète à l’aide de ces courbes. Le sens des flèches indique la direction dans laquelle les profits augmentent. Ainsi, la courbe d’isoprofit de la firme A est tangente à la droite horizontale passant par sa fonction de réaction indiquant que la firme A maximise son profit pour une stratégie donnée de la firme B. Les courbes d’isoprofit de la firme B sont verticales sur sa courbe de réaction. Les effets de report sont positifs comme l’indiquent les flèches orientées vers le nord-est (points du plan (zA, zB) où les profits des deux firmes augmentent). L’accroissement de l’effort stratégique d’une firme le long de sa fonction de réaction augmente le profit de l’autre firme qui ne modifie pas sa stratégie. Les profits situés aux équilibres nord-est sont donc supérieurs à ceux situés au sud-ouest. Les effets de report de même signe (sign∈(∂∏A / ∂zB) = sign∈(∂∏B / ∂zA)), impliquent que ce raisonnement vaut pour chaque firme.
Si la multiplicité d’équilibres n’est pas une propriété spécifique des économies comportant de tels défauts, leur ordonnancement en termes de bien-être leur est spécifique. La politique économique est nécessaire car aucun agent pris isolément ne peut conduire l’économie vers un équilibre haut lorsque l’économie reste bloquée à un équilibre bas. Se pose alors le problème d’un mécanisme endogène susceptible de coordonner les agents sur un équilibre supérieur.
1.3 Indétermination et sélection des équilibres
L’élimination des défauts de coordination suppose que les équilibres sont déterminés. Le problème de l’indétermination de l’équilibre se pose principalement dans les modèles à équilibres multiples (chez Arrow-Debreu, ils sont localement déterminés). Les modèles étudiés rencontrent deux problèmes : les équilibres sont indéterminés et particuliers (continuum d’équilibres). Si on restreint l’étude aux modèles avec un nombre limité d’équilibres isolés, ceux-ci sont localement uniques mais pas globalement uniques. Si les modèles sont appropriés pour l’analyse locale, ils requièrent une dynamique explicite pour l’application de politiques économiques.
La détermination d’un équilibre a deux aspects : la statique comparative et son caractère prévisionnel. Les modèles à équilibres localement uniques mais non globalement uniques ne peuvent être utilisés que pour la statique comparative, alors que les modèles à équilibres globalement uniques peuvent être utilisés pour l’analyse de statique comparative globale. L’existence d’équilibres multiples peut ainsi altérer le pouvoir de prédiction de tels modèles. Cependant, celles-ci peuvent être faites dans les modèles statiques avec équilibres localement uniques seulement si les équilibres sont complétés par une analyse dynamique et si les conditions initiales sont précisées. L’élimination d’un défaut de coordination par sélection d’un équilibre haut suppose donc d’expliciter la dynamique de transition d’un équilibre bas vers un équilibre haut. Cooper (1994) fait une hypothèse qui permet de sélectionner un équilibre en présence d’une multiplicité d’équilibres de Nash Pareto ordonnés[8]. L’hypothèse consiste à supposer que les agents conditionnent leurs croyances aux comportements stratégiques des autres dans la mesure où l’histoire du jeu crée un point focal. Cette procédure de sélection peut produire des phénomènes dynamiques possédant un caractère autoréalisateur. Les périodes associées à des comportements d’équilibre optimistes engendrent généralement des croyances optimistes pour les périodes futures et inversement en cas d’anticipations pessimistes.
Une autre approche, valable uniquement pour la sélection des équilibres à anticipations rationnelles, repose sur le critère d’E-stabilité (DeCanio, 1979; Lucas, 1986). L’idée consiste à étudier la formation des anticipations en dotant les agents d’un processus d’apprentissage adaptatif[9] (Evans et Honkapohja, 1994). Les agents agissent en économètres et cherchent à estimer les paramètres d’un modèle à anticipations rationnelles au moyen de procédures d’apprentissage statistiques. La convergence de leurs estimations vers les valeurs des « vrais » paramètres de la régression à anticipations rationnelles est gouvernée par les conditions d’E-stabilité[10]. Considérons les équilibres à anticipations rationnelles d’un modèle et supposons que la solution particulière du modèle considéré représente un processus stochastique (la valeur moyenne d’un k-cycle ou les paramètres d’un processus autorégressif). Sous l’hypothèse d’apprentissage adaptatif, les agents ne connaissent pas le vecteur des paramètres mais l’estiment en utilisant une procédure statistique (par exemple les moindres carrés). Le problème est de savoir si l’estimation faite au temps t s’identifie à la solution particulière du modèle lorsque t tend vers l’infini. Sous certaines conditions sur les paramètres, la convergence est assurée (Evans et Honkapohja, 1999).
2. Chômage d’équilibre et externalités de demande agrégée
Les défauts de coordination peuvent résulter d’un problème d’externalités de demande agrégée. De telles externalités sont liées aux complémentarités créées par les interactions de demande entre agents dans des économies de concurrence imparfaite à plusieurs secteurs (Heller, 1986). L’idée générale est qu’une économie peut demeurer coincée à un équilibre bas car les ventes de certains agents peuvent être limitées par les achats d’autres agents qui ne peuvent pas se coordonner.
2.1 Les externalités de demande agrégée d’une économie décentralisée
Les externalités de demande agrégée ont trait aux externalités engendrées par les interactions de demande entre agents dans des économies décentralisées. Une externalité de demande existe lorsque les agents utilisent les prix et les quantités comme informations afin d’établir leurs choix. Un des intérêts de cette approche est que les ajustements de prix et de quantité sont complémentaires. Les problèmes de coordination afférents à ces externalités n’existent pas dans une économie walrasienne étant donné que les agents peuvent vendre et/ou acheter les quantités désirées aux prix et salaires en vigueur[11]. Les modèles d’échecs de coordination fondés sur de telles externalités s’incarnent dans des économies de concurrence imparfaite composées de plusieurs secteurs reliés entre eux. Deux types d’hypothèses sont généralement retenus. Premièrement, les fonctions de demande possèdent des propriétés microéconomiques standard, d’une part, les fonctions de demande individuelles de bien sont décroissantes de leur prix[12] (absence de bien Giffen) et d’autre part, les courbes d’Engel sont croissantes pour chaque agent. Deuxièmement, il est supposé que les agents ne consomment pas les biens qu’ils possèdent ou bien qu’ils produisent mais consomment toujours les biens produits par les autres. Dans une économie décentralisée, de nombreux biens échangés sur les marchés sont produits et consommés. Chaque entreprise est spécialisée dans la production d’un bien et chaque consommateur est acheteur des différents biens. Cette hypothèse centrale traduit l’organisation des échanges propres aux économies décentralisées[13].
Le jeu des complémentarités stratégiques diffère selon le type d’économie étudiée. Deux voies sont généralement suivies. La première est l’approche de Cournot-Nash généralisée à plusieurs secteurs avec plusieurs entreprises par secteur. Dans chaque secteur, des firmes produisent un bien identique et déterminent leur niveau de production en prenant les stratégies des autres entreprises de leur secteur comme données et en tenant compte de la courbe de demande de l’industrie déterminée par le niveau d’activité des autres secteurs. Comme chez Cournot, les quantités produites sont substituts stratégiques au sein de chaque secteur (fonctions de réaction décroissantes). Par contre, il existe des complémentarités stratégiques intersectorielles qui émanent des effets de revenu. Ainsi, une augmentation du niveau de l’activité dans les autres secteurs augmente la demande qui s’adresse à un secteur donné et crée une incitation à accroître le niveau de l’activité. Le lien entre les secteurs repose sur la relation entre le revenu courant et les dépenses courantes. L’hypothèse selon laquelle les agents consomment le bien produit par d’autres est donc essentielle. Les modèles de Drazen (1987), Hart (1982) et Heller (1986) sont issus de cette approche[14]. Par exemple, Heller montre que, malgré l’existence d’un système complet de marchés, il peut exister des problèmes de coordination similaires à ceux engendrés par la présence de marchés incomplets. Il donne les conditions nécessaires[15] sur les fonctions de demande pour engendrer une multiplicité d’équilibres de Nash Pareto ordonnés. La deuxième est l’approche de concurrence monopolistique qui est une extension de la précédente avec produits différenciés (index de consommation CES). Dans ce type d’économie, chaque entreprise offre un unique bien dont elle détient le monopole de production et maximise son profit (en produisant un bien final ou un bien intermédiaire) en prenant la demande agrégée comme donnée. Les modèles de Weitzman (1982), Solow (1986), Startz (1986), Kiyotaki (1988) et Manning (1990) se réclament de cette approche[16]. Dans cette optique, les processus d’entrée et de sortie de firmes peuvent être à l’origine de propagations de chocs technologiques (Pagano, 1990; Horstein, 1993). La différence essentielle entre les deux types d’approches réside dans l’origine du pouvoir de marché. Dans les modèles à la Cournot-Nash, le pouvoir de marché est paramétré par le nombre de firmes; il est d’autant plus grand que le nombre de vendeurs pour chaque bien est faible. Dans le modèle de concurrence monopolistique, il dépend du degré de substituabilité entre biens. Cette différence importe si l’on cherche à caractériser la nature des complémentarités stratégiques et l’influence des multiplicateurs. Le modèle suivant développe un exemple d’une économie à la Cournot-Nash.
2.2 Un modèle de chômage involontaire en régime de prix et salaires flexibles
Nous proposons ici une version simplifiée du modèle de Roberts (1987) qui se propose de montrer la possibilité d’existence d’équilibres multiples avec chômage involontaire dans une économie de concurrence imparfaite en régime de prix et salaires flexibles. Ce modèle s’incarne dans un jeu séquentiel avec des équilibres parfaits en sous-jeux.
Soit une économie à cinq biens X, Y, R, S et M et quatre types d’agents A, B, J et K. Les agents de types A et B sont les entreprises, indicées j(j = 1, 2, ..., n) et les agents de types J et K sont les consommateurs, indicés i(i = 1, 2, ..., n). Les biens X et Y sont les biens de consommation produits, R et S sont les facteurs de production et M est la monnaie unité de compte (les prix sont monétaires) et intermédiaire des échanges. Les quantités de biens et de monnaie sont respectivement notées x, y, r, s et m. L’économie s’organise ainsi en quatre marchés, à savoir deux marchés pour les biens et deux marchés pour les facteurs de production.
Les entreprises de types A et B dérivent leur utilité de la consommation de bien M. Les fonctions d’utilité de chaque firme de type A et de type B s’écrivent respectivement VA(x, y, r, s, m) = UA(m) et VB(x, y, r, s, m) = UB(m) . Ces fonctions sont supposées continues et strictement croissantes par rapport à la quantité de monnaie. On suppose une spécialisation dans la production qui stipule qu’une firme ne peut disposer de toutes les technologies disponibles. Ainsi, chaque firme de type A produit le bien X en utilisant l’intrant R et chaque firme de type B produit le bien Y en utilisant l’intrant S. Les technologies sont à rendements constants[17]. Les firmes ne peuvent produire des quantités positives de bien sans utiliser de travail. Les vecteurs de dotations initiales des firmes de types A et B sont eA = (0, 0, 0, 0, m̄A) et eB = (0, 0, 0, 0, m̄B), où m̄A et m̄B sont leurs dotations en monnaie. Elles doivent donc acheter du travail afin de produire.
Chaque consommateur de type J(K) dispose d’une dotation r̄J (s̄K) en travail R(S) et d’une dotation m̄J( m̄K) en monnaie M. Les vecteurs de dotations initiales des consommateurs de types J et K sont donc eJ = (0, 0, r̄J, 0, m̄J) et eK = (0, 0, 0, s̄K, m̄K). Les préférences des consommateurs de types J et K sont représentées par les fonctions d’utilité UJ(y, r̄J – r, m) et UK(x, s̄K – s, m). Ces fonctions sont continues, strictement croissantes en leurs arguments, strictement quasi concaves et tendent vers –∞ si m < 0 (afin d’éviter les endettements excessifs). L’écriture des fonctions d’utilité reflète l’organisation non fordienne des marchés qui traduit le caractère décentralisé de l’économie : les consommateurs de type J(K) vendent leur travail aux entreprises de type A(B) et achètent le bien produit par les entreprises de type B(A).
Quelques précisions sont nécessaires quant à la manière dont les agents choisissent leurs stratégies et interagissent. La structure du jeu est telle que les agents ont une parfaite connaissance du fonctionnement de l’économie. Ainsi, il n’existe pas d’incertitude exogène, pas d’information privée concernant les préférences et les dotations des agents et aucune confusion pour un agent sur les actions des autres ainsi que sur leurs issues possibles. Le jeu est donc à information parfaite et complète. Une stratégie pure pour un agent est un plan spécifiant l’action à choisir dans chaque circonstance, compte tenu de l’information disponible au moment où il prend sa décision. Une stratégie pour un consommateur est une paire de vecteurs de quantités demandées de bien et offertes de travail compte tenu des prix et des salaires annoncés par les firmes. Une stratégie pour une firme consiste en la spécification de deux prix (prix du bien produit et salaire) et de deux vecteurs de quantités (bien et travail), compte tenu des annonces des consommateurs et des contraintes de faisabilité des échanges. Chaque agent forme des conjectures correctes sur les choix effectués par les autres mais aussi sur leurs réactions quant à ses propres choix[18].
Les modalités de détermination des prix et des quantités obéissent à une logique séquentielle. Au début, chacune des 2n entreprises annonce un prix unique pour les quantités du bien qu’elle vend et un salaire unique pour les quantités d’intrant qu’elle achète. De telles annonces sont faites indépendamment et simultanément. On a deux vecteurs de prix pour les biens produits, soit pX = (p1A, p2A, ..., pnA) et pY = (p1B, p2B, ..., pnB), et deux vecteurs de salaires pour les intrants, soit wR = (w1A, w2A, ..., wnA) et wS = (w1B, w2B, ..., wnB). Ensuite, compte tenu de ces prix monétaires, chaque consommateur annonce simultanément et indépendamment des autres les quantités qu’il désire acheter et vendre. Ainsi, chaque agent de type J annonce un vecteur de quantités qu’il désire acheter, soit yiJ = (yi1J, yi2J, ..., yinJ ) et un vecteur d’intrants qu’il désire vendre, soit riJ = (ri1J, ri2J, ..., rinJ ). Chaque agent de type K annonce les vecteurs xiK = (xi1K, xi2K, ..., xinK ) et siK = (si1K, si2K, ..., sinK ). L’effectivité des plans requiert qu’un consommateur ne peut vendre plus de travail que ce que sa dotation lui permet d’offrir, c.-à-d. ∑jrijJ ≤ r̄iJ et ∑jsijK ≤ s̄iK. Après ces annonces, chaque firme décide des quantités de bien qu’elle vend et d’intrants qu’elle achète. Chacune de ces quantités est limitée par les offres et demandes des consommateurs avec qui elles échangent. Ainsi, chaque firme de type A détermine un vecteur de quantités du bien à vendre, soit xjA = (x1jA, x2jA, ..., xnjA ) et un vecteur de quantités d’intrant à acheter, soit rjA = (r1jA, r2jA, ..., rnjA ) sous contraintes technique de faisabilité des plans, soit ∑ixijA ≤ ∑irijA avec xjA = rjA, et de volontarité des échanges, soit xijA ≤ xijK et rijA ≤ rijJ. Cette analyse vaut pour les firmes de type B.
Les échanges monétaires sont bilatéraux et décentralisés par marché. Chaque consommateur de type J achète du bien Y en quantités ∑jyijB qu’il paye et vend les quantités de travail ∑jrijA pour lesquelles il reçoit un revenu ∑jwjArijA. Les allocations finales en bien, en travail et en monnaie de chaque agent de type J sont yijJ = yijB, rijJ = r̄ijJ – rijA et miJ = m̄iJ + ∑jwjArijA – ∑jpjByijB. Cette analyse s’applique pour chaque agent de type K. Chaque firme de type A perçoit un revenu ∑ipjAxijA suite a ses ventes et dépense ∑iwjArijA. La dotation finale en monnaie de chaque firme de type A est donc mjA = ∑ipjAxijA – ∑iwjArijA + m̄jA. L’analyse s’applique pour chaque firme de type B. L’issue des transactions détermine un équilibre.
DéfinitionUne solution walrasienne pour cette économie est constituée d’un vecteur de prix < pX, pY, wR, wS > et d’une allocation < (xjA, rjA), (yjB, sjB), (yiJ, riJ), (yiK, siK) > tels que :
(xjA, rjA) maximise UA( m̄A + pXx – wRr) sous contraintex ≤ r, j = 1, 2, ..., n;
(yjB, sjB) maximise UA( m̄B + pYy – wSs) sous contraintey ≤ s, j = 1, 2, ..., n;
(yiJ, riJ) maximiseUJ(y, –rJ – r,m̄J – pYy + wRr), i = 1, 2, ..., n;
(yiK, siK) maximiseUK(x, –sK – s, m̄K – pXx – wSs), i = 1, 2, ..., n;

Les conditions (i), (ii), (iii) et (iv) traduisent respectivement la maximisation de l’utilité (profit) des entreprises et des consommateurs alors que (v) est la condition d’apurement des marchés.
Proposition 2Il existe un continuum d’équilibres Pareto ordonnés : un des équilibres est de plein-emploi et les autres sont des équilibres avec différents niveaux de chômage involontaire.
Preuve pour l’équilibre walrassien. Une firme qui dévie de la situation walrassienne se retrouve avec un niveau d’activité équivalent à l’allocation résultant d’une situation autarcique. Supposons qu’à la première étape du jeu chaque firme annonce le même prix pour le bien qu’elle produit, soit (pjA, pjB) = (pX, pY), et le même salaire pour l’intrant qu’elle utilise, soit (wjA, wjB) = (wR, wS). Supposons qu’à la deuxième étape chaque consommateur commande les quantités de bien désirées, soit (yiJ, xiK), et offre les quantités de travail désirées, soit (riJ, siK). Dans la troisième étape, les firmes ont intérêt à satisfaire la demande en offrant (xjA, yjB) = (xiK, yiJ) et à demander les quantités de travail offertes en embauchant (rjA, sjB) = (riJ, siK). Aux prix et salaires walrassiens, aucun agent n’a donc intérêt à dévier unilatéralement en faisant d’autres propositions d’échange.
Preuve pour les équilibres keynésiens. Un équilibre keynésien désigne une situation dans laquelle k agents reçoivent leur allocation walrassienne et (n – k) agents consomment leur allocation initiale[19]. Il faut vérifier que les agents n’ont pas intérêt à dévier des quantités échangées et que la flexibilité des prix et des salaires ne profite à personne. Les firmes qui réalisent des transactions optimales avec chacun des consommateurs i ≤ k non rationnés n’ont pas intérêt à dévier. Si chaque agent rationné i > k décide d’offrir son travail, alors les firmes n’ont pas intérêt à les employer car leurs débouchés resteront inchangés. Le caractère non coopératif du jeu exclut d’emblée toute concertation des chômeurs pour modifier leur proposition de vente de travail aux firmes susceptibles de les employer[20]. De plus, si chaque agent rationné envoie des signaux de demande, les firmes ne disposent pas des intrants nécessaires pour produire. Supposons maintenant qu’une firme décide de dévier des prix et salaires walrassiens. Les rendements constants permettent à la firme dont les propositions d’achat s’élèvent de satisfaire cette nouvelle demande en augmentant sa production. En dehors du cas particulier où les prix diminuent et les salaires augmentent, le chômage persistera. Ainsi, si une firme décide d’accroître (de diminuer) les prix et les salaires, alors elle perd (gagne) des clients qui achètent aux firmes dont le prix est moins élevé et n’a ainsi aucune incitation à embaucher (elle perd des salariés et ne peut satisfaire la demande). Si elle accroît ses prix et diminue les salaires, alors elle perd ses parts de marché et ses salariés.
L’approche proposée ici comporte des caractéristiques intéressantes mais aussi des limites. D’abord, le chômage d’équilibre est involontaire dans la mesure où certains agents peuvent se trouver en dehors de leur courbe d’offre de travail (les équilibres sont paramétrés par les anticipations de demande des firmes qui déterminent le niveau d’emploi). De plus, la flexibilité des prix et des salaires est généralement inadaptée pour éliminer les rationnements. Néanmoins, la distinction entre rationnement et activité de recherche d’emploi n’est pas faite. Il conviendrait d’intégrer les comportements de prospecteurs d’emploi qui détermineraient les conditions dans lesquelles un contrat de travail est, de leur point de vue, acceptable ou non. On retrouve la critique adressée par Lucas (1987) à l’encontre du concept de chômage involontaire. Ensuite, l’origine du chômage est à rechercher dans un problème de communication de la demande effective dans la mesure où le caractère décentralisé des échanges ne permet pas de coordonner efficacement les actions des agents. Les entreprises peuvent en effet subir des contraintes de débouchés sur les marchés des biens ce qui ne les incite pas à embaucher davantage. Ce problème de communication est lié à la structure du jeu[21] (schéma de rencontres et simultanéité des décisions qui amplifient les conséquences des anticipations éventuellement pessimistes des entreprises). Si les agents avaient la possibilité de se rencontrer à de multiples reprises en modifiant par exemple la structure du jeu[22] (Jones et Manuelli, 1992), alors le résultat du jeu serait modifié. Enfin, la nature des schémas de rationnement n’est pas précisée (file d’attente ou proportionnel). Ainsi, la prise en considération, à l’équilibre, de l’organisation et de la réalisation des échanges requiert d’intégrer d’autres manifestations de la décentralisation comme les frictions et les coûts de transaction qui peuvent influencer les modalités de détermination du niveau de l’activité et de l’emploi.
3. Chômage d’équilibre et externalités d’échange
Les défauts de coordination peuvent provenir d’externalités relatives à la décentralisation des échanges. Dans ce contexte, les interactions entre agents ressortent principalement des modalités d’organisation et de réalisation des transactions. Deux voies peuvent être empruntées : les frictions (Diamond, 1982, 1984) ou les coûts de transaction (Howitt, 1985; Howitt-McAfee, 1987). L’approche des externalités d’échanges est importante dans la mesure où le chômage d’équilibre avec prix et salaires flexibles est compatible avec la concurrence parfaite.
3.1 Frictions dans les échanges et défauts de coordination
L’activité d’échange peut constituer une source de défauts de coordination. La détermination des grandeurs n’est alors pas indépendante de la façon dont les agents se rencontrent et concluent leurs transactions. Dans la théorie de l’équilibre général concurrentiel, la coordination des échanges s’effectue de manière centralisée à l’équilibre au sein de la chambre de compensation. Toutes les transactions sont sans délais et sans coût (coût d’identification, de rencontre et de négociation) si bien qu’elles se limitent à la répartition de l’allocation d’équilibre déterminée indépendamment des conditions de l’échange. Le problème n’est pas que les transactions en déséquilibre ne sont pas modélisées mais plutôt que la prise en compte des transactions a des conséquences sur la détermination du niveau de l’activité et de l’emploi. Dans une économie décentralisée, il n’existe pas de chambre de compensation (Diamond, 1987). Si le secrétaire de marché est éliminé ou si son rôle se restreint à la détermination des prix et des salaires d’équilibre, il peut exister des frictions (information imparfaite, délais de rencontre) et/ou des coûts de transaction liés au degré de participation des agents sur les marchés. Les externalités d’échange sont la conséquence de la prise en compte par les agents de l’activité d’échange.
Lorsque l’activité d’échange importe, l’interaction entre agents ne repose pas directement sur les préférences ou la production. La participation à l’échange est une activité qui procure un gain mais qui est aussi entachée d’un coût de recherche. La fonction de gain dépend du nombre d’agents qui participent à l’échange. Les gains sont supposés augmenter avec la taille du marché donnée par le taux de participation (externalité positive). Lorsque la taille du marché augmente, le coût de recherche diminue. La décision de participation consiste à comparer les gains avec le coût qui est donné ou distribué aléatoirement. Chaque agent détermine un coût de production critique et choisit de participer si le gain espéré dans l’échange excède le coût perçu, c.-à-d. si le coût afférent à la participation est inférieur à son coût critique[23]. Un équilibre décrit une situation dans laquelle, compte tenu d’un certain taux de participation, les agents pour lesquels le coût n’excède pas le coût critique vont effectivement participer. Si ce taux est celui qui a servi d’information aux agents qui ont choisi de participer, alors l’équilibre est autoréalisant. La multiplicité d’équilibres provient de la validation des croyances sur ce taux qui peut être élevé ou faible. En raison de l’externalité positive, l’ordonnancement des équilibres dépend de la valeur du taux de participation.
Diamond (1982, 1984) systématise les externalités de participation en insistant sur les problèmes de rencontres dans des économies décentralisées[24]. À un instant donné, l’économie se compose d’agents dotés d’une unité de bien ou de monnaie à échanger et d’agents sans pouvoir d’achat (les chômeurs en attente d’un projet de production). La production et les échanges relèvent d’un processus stochastique (délais). Les agents doivent échanger le bien qu’ils produisent pour consommer. La technologie de rencontres est à rendements croissants et les rencontres sont bilatérales et aléatoires. L’utilité des agents dépend positivement de la consommation et négativement du coût de production qui doit être déterminé. Ainsi, les chômeurs doivent décider d’un niveau de coût de production pour lequel ils sont prêts à produire compte tenu du fait que les projets de production se présentent à eux de manière aléatoire. La décision de production, c.-à-d. le choix d’un coût de production, dépend des gains espérés dans les échanges. De tels gains dépendent du nombre d’échangistes. Or le nombre d’agents présents dans le secteur des échanges dépend lui-même du nombre de projets de production mis en oeuvre. Cette interaction entre les décisions de production et le nombre de rencontres illustre le jeu des complémentarités stratégiques et des effets de report[25]. Diamond montre l’existence d’une multiplicité d’équilibres stationnaires associés à différents niveaux de chômage sans présupposer la rigidité des prix et des salaires[26]. Deux problèmes d’importance inégale nous invite à délaisser ces modèles et à considérer l’approche en termes de coûts de transaction. Premièrement, les externalités dans les transactions ne concernent que les rencontres mais pas les dénouements relatifs à un échange. Ainsi, les problèmes associés à la coïncidence réciproque des besoins sont éludés soit en supposant que l’échange de troc est toujours possible (Diamond, 1982), soit en éludant le problème de l’acceptation de la monnaie[27] (Diamond, 1984). Deuxièmement, l’existence d’une multiplicité d’équilibres avec différents niveaux de chômage est étroitement liée à la présence de rendements croissants dans la technologie de rencontres. Or une telle hypothèse n’est pas nécessaire aux échecs de coordination comme en atteste le modèle suivant.
3.2 Chômage d’équilibre et coûts de transaction
La participation des agents sur les marchés peut engendrer des externalités dans les transactions (Chatterjee et Cooper, 1989). L’approche par les coûts de transactions consiste à introduire des coûts d’échange dans l’équilibre général walrassien (Howitt et McAfee, 1987; Howitt, 1990). Nous proposons ici une version simplifiée du modèle d’Howitt (1985) qui constitue la référence en la matière.
3.2.1 L’économie et les coûts de transaction
Soit une économie de concurrence parfaite à deux marchés, un pour le bien produit et un pour le travail. Il existe deux types d’agents : H consommateurs identiques indicés h et J entreprises identiques indicées j. Le secrétaire de marché détermine les prix et les salaires d’équilibre mais n’organise pas les échanges (absence de chambre de compensation). Les échanges sont assortis de coûts de transaction qui prennent la forme de coûts de communication. Il existe une relation entre la taille d’un marché et de tels coûts : les coûts unitaires sont inversement proportionnels aux transactions réalisées. Ces coûts, mesurés en termes réels, modifient la conception de l’échange car les agents font des efforts d’achat et de vente. Ainsi, le coût unitaire de vente consenti par un vendeur est une fonction décroissante de l’effort d’achat consenti par les acheteurs. Nous omettons pour simplifier l’influence des externalités au sein d’un même groupe d’agents. Chaque acheteur consent un effort d’achat proportionnel à la quantité achetée tandis que chaque vendeur consent un effort de vente inversement proportionnel à l’effort effectué par les acheteurs. Ainsi, la vente d’une quantité yj coûte sjY à l’entreprise j, soit sjY(yj) = yj / bY, où bY est l’effort d’achat des consommateurs. L’effort d’achat des consommateurs est proportionnel à la quantité de bien Y échangée sur le marché du bien. On a donc bY = βYY, avec βY ∈[0, 1]. Le coût de vente unitaire du bien pour l’entreprise j est η = sjY / yj, soit η(Y) = 1 / βYY, ∀j. La vente d’une quantité de travail nh coûte shN au consommateur h soit shN(nh) = nh / bN, où bN est l’effort d’achat des firmes. L’effort d’achat des firmes est proportionnel à la quantité N de travail échangée sur le marché du travail, soit bN = βNN, avec βN ∈[0, 1]. Le coût de vente unitaire du travail pour le consommateur h est τ = shN / nh, soit τ(N) = 1 / βNN, ∀h. Les agents n’ont aucune influence sur les coûts de transaction qui sont intégrés dans les plans de production et de consommation.
3.2.2 Les entreprises et les consommateurs
Afin de vendre la quantité yj sur le marché du bien, l’entreprise j doit produire la quantité (1 + η(Y)) yj. Ainsi, à la quantité produite yj correspond la quantité vendue yj / (1 + η(Y)). Afin de produire, l’entreprise j doit acheter du travail. Si elle décide d’acheter la quantité nj, elle ne peut utiliser que la quantité (1 – βN) nj pour produire. La fonction de production F est supposée continue, croissante et strictement concave. En notant p et w le prix du bien et le salaire nominal, le programme de l’entreprise j s’écrit :
La condition d’optimalité (1 – βN) Fnj((1 – βN) nj)) / (1 + η(Y)) = w / p traduit l’égalité de la productivité marginale du travail avec le salaire réel. On déduit les fonctions d’offre de bien et de demande de travail de l’entreprise j :
Ces fonctions sont toutes deux décroissantes du salaire réel et croissantes de la quantité de bien échangée. L’offre de bien et la demande de travail agrégées sont F((1 – βN) N) / (1 + η(Y)) et Nd.
La fonction d’utilité du consommateur h est U(yh) – c(nh), où yh est la quantité de bien consommée et nh la quantité de travail offerte dont la limite supérieure est –nh > 0. U est continue, strictement croissante et strictement quasi concave. La fonction de coût c est continue, croissante et convexe sur [0, –nh]. À cause des coûts de transaction, l’agent h qui achète la quantité yh et vend la quantité nh ne consomme que la quantité (1 – βY) yh et doit offrir la quantité (1 + τ(N)) nh. L’agent h reçoit des parts de profits, soit ![]() Il choisit les quantités yh et nh qui maximisentson utilité sous la contrainte que ses dépenses n’excèdent pas ses revenus :
Il choisit les quantités yh et nh qui maximisentson utilité sous la contrainte que ses dépenses n’excèdent pas ses revenus :
La condition d’optimalité, c.-à-d. (1 + τ(N)) cnh ((1 + τ(N)) nh) / ((1 – βY) Uyh((1 – βY) yh)) = w / p, traduit l’égalité entre le salaire réel et le taux marginal de substitution entre consommation et loisir. On déduit la fonction d’offre de travail et la fonction de demande de bien du consommateur h :
Ces fonctions sont croissantes du salaire réel et du niveau de l’emploi. L’offre agrégée de travail est Ns.
3.2.3 Équilibres de sous-emploi persistant
Définition 1Un équilibre général avec coûts de transaction est un vecteur ((w / p)*, Y*, N*) qui satisfait les trois conditions suivantes :
La condition (i) traduit l’équilibre sur le marché du travail. L’équilibre requiert que les signaux quantités, pris comme donnés par les agents, correspondent aux quantités échangées à l’équilibre. Ainsi, les conditions (ii) et (iii) stipulent respectivement que la quantité de travail échangée N est égale à la quantité d’équilibre Ns et que les quantités de bien vendues Y sont égales à la quantité produite F(N(1 – βN)) moins les coûts afférents aux échanges sur le marché du bien Yη(Y). Le système (i)-(iii) a trois équations et trois inconnues. Il détermine le salaire réel d’équilibre et les quantités de bien et de travail échangées à l’équilibre.
Définition 2Le chômage désigne la quantité de travail nécessaire à la vente de travail. Le niveau de chômage sur le marché est ![]()
Proposition 3Il existe une multiplicité d’équilibres de sous-emploi avec chômage involontaire ordonnés en termes de bien-être.
Preuve. On montre graphiquement la multiplicité (l’annexe 1 montre l’ordonnancement parétien). La condition (iii) est équivalente à Y = Y(N). À l’équilibre, N satisfait la condition :
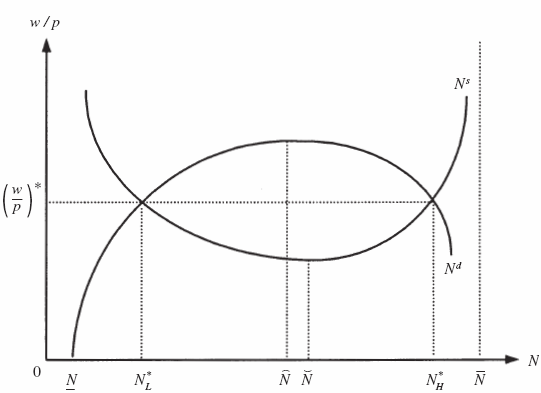
Cette condition d’équilibre est restreinte au marché du travail. En l’absence d’externalités (η et τ constants), les conditions (ii) et (iii) n’ont aucune pertinence et le niveau d’emploi d’équilibre (optimal) est déterminé par l’égalité entre productivité marginale du travail, taux marginal de substitution entre consommation et loisir, et salaire réel. En présence d’externalités dues aux coûts de transaction, les courbes d’offre et de demande de travail peuvent se rencontrer à plusieurs reprises[28] (ici deux). Ainsi, la courbe d’offre de travail peut être décroissante pour de faibles niveaux d’emploi. Lorsque l’effort de vente des salariés augmente, le coût unitaire de vente du travail s’accroît ce qui tend à diminuer le prix d’offre du travail et à compenser l’accroissement de la désutilité marginale du travail ![]() Cependant pour des niveaux d’emploi plus élevés, l’effort de vente diminue et les coûts de transaction aussi. La courbe d’offre de travail retrouve alors une allure normale
Cependant pour des niveaux d’emploi plus élevés, l’effort de vente diminue et les coûts de transaction aussi. La courbe d’offre de travail retrouve alors une allure normale ![]() De plus, la courbe de demande de travail peut être croissante : lorsque l’emploi augmente, le coût unitaire de vente du bien diminue (l’effort d’achat augmente) ce qui tend à accroître la demande de travail
De plus, la courbe de demande de travail peut être croissante : lorsque l’emploi augmente, le coût unitaire de vente du bien diminue (l’effort d’achat augmente) ce qui tend à accroître la demande de travail ![]() Pour certains niveaux d’emploi, les externalités ne suffisent pas à compenser la décroissance de la productivité marginale du travail
Pour certains niveaux d’emploi, les externalités ne suffisent pas à compenser la décroissance de la productivité marginale du travail ![]()
Graphique 2
Équilibres multiples et coûts de transaction
L’approche des coûts de transaction possède des propriétés intéressantes[29]. D’abord, le salaire réel a une dynamique contracyclique car il peut demeurer identique aux deux équilibres en dépit de la flexibilité des prix et des salaires. Ensuite, le modèle est d’une généralité plus grande que celui de Roberts (1987) dans la mesure où le résultat de chômage d’équilibre est obtenu en concurrence parfaite (les agents prennent les prix et les coûts comme donnés et ne subissent pas de contraintes de débouchés; s’ils désirent échanger plus, ils doivent accepter d’encourir des coûts plus élevés). De plus, les interactions interindividuelles n’épuisent pas tous les échanges mutuellement avantageux car les signaux prix et quantités sont complémentaires dans la détermination du niveau de l’emploi. Il s’agit d’une propriété keynésienne car l’ajustement par les prix peut ne pas suffire à éliminer les inefficacités. Enfin, le chômage d’équilibre, qui se définit comme le nombre d’heures de travail non payées et nécessaire pour vendre une quantité de travail, peut être considéré comme involontaire. Considérons les deux équilibres du graphique 2. Afin de vendre la quantité nL chaque agent doit dépenser le montant nLτ(NL) au lieu du montant nLτ(NH) qui serait nécessaire si l’économie se trouvait à l’équilibre haut. Le chômage est donc mesuré par nL(τ(NL) – τ(NH)). À l’équilibre bas, les agents préféreraient se coordonner sur l’équilibre haut (qui n’est pas optimal à cause des coûts de transaction). Cependant, aucun agent n’a intérêt à dévier en consentant un effort plus important que les autres[30].
L’approche des coûts de transaction comporte néanmoins certaines limites. D’abord, le résultat de chômage involontaire est critiquable. En effet, les agents sont tous sur leur courbe d’offre si bien que le marché du travail est toujours équilibré. En ce sens, il n’y pas de rationnement involontaire mais seulement des équilibres de sous-emploi Pareto ordonnés. Le modèle ne distingue donc pas le rationnement de l’activité de recherche d’un emploi même si les plans d’achat et de vente sont liés aux efforts de recherche des agents. Ensuite, il ne suffit pas d’intégrer les coûts de transaction dans les plans des agents pour rendre compte de l’effectivité des échanges. Le modèle précédent détermine effectivement des prix et des quantités d’équilibre tels que les quantités ne sont pas allouées de manière optimale. Cependant, si l’équilibre est défini à partir d’hypothèses sur l’organisation des échanges, il n’est pas montré que les prix et les quantités déterminées résultent de la réalisation décentralisée des transactions. Ainsi, il n’est pas possible de déduire des conditions d’équilibre général (i)-(iii) une proposition relative aux individus (bien-être individuel) qui dépend essentiellement d’une condition d’égalité décentralisée énonçant que toute allocation individuelle réalisée est identique à toute allocation désirée à moins de présupposer l’absence de problèmes dans la réalisation des échanges[31]. La prise en compte explicite des modalités de rencontres et de réalisation des transactions a néanmoins des conséquences sur la détermination du taux de chômage. On retrouve ici le rôle joué par les frictions dans l’échange décentralisé[32]. Enfin, aucune solution n’est proposée dans ce type de modèle pour lever le défaut de coordination. Deux raisons sont invoquées. Premièrement, la procédure de sélection de l’équilibre haut sur lequel les agents pourraient se coordonner n’est pas formalisée. Deuxièmement, la politique économique ne peut être envisagée dans la mesure où les exercices de statique comparative sont rendus inopérants par le fait que la stabilité locale des équilibres est délaissée[33]. L’approche suivante a pour vocation de dépasser cette dernière limite dans la mesure où elle propose un cadre conceptuel propice à la politique économique.
4. Chômage d’équilibre et externalités de rendements croissants
Les défauts de coordination n’ont pas toujours pour origine des problèmes de communication de demande ou des problèmes de rencontres. Ils peuvent trouver leur origine dans des externalités de rendements croissants issus de la technologie de production (Weitzman, 1982; Kiyotaki, 1988; Manning, 1990; Pagano, 1990; Rivard, 1994 ou Cooper et Corbae, 2002). La prise en compte des rendements croissants permet de doter l’approche des défauts de coordination d’une dynamique qui lui fait souvent défaut et d’envisager des applications de politique économique.
4.1 Rendements croissants et défauts de coordination
La littérature consacrée aux échecs de coordination avec rendements croissants peut être divisée en trois catégories selon le contexte dans lequel ils se manifestent. La première catégorie de modèles utilise les rendements croissants dans les problèmes de communication de demande entre agents. La référence est le modèle de concurrence imparfaite de Weitzman (1982). Dans ce modèle, le chômage d’équilibre est causé par une absence de coordination dans les dépenses due à un problème de communication de la demande agrégée. Il montre l’existence d’une multiplicité d’équilibres de sous-emploi Pareto ordonnés. La deuxième catégorie de modèles s’appuie sur le degré de participation des agents sur les marchés. Les externalités relatives aux effets de participation des agents (rendements croissants dans la technologie de rencontres) sont étudiées dans le modèle de Diamond (1984) et plus récemment chez Pissarides (2000). Dans un modèle qui intègre les cycles d’affaires endogènes, Diamond et Fudenberg (1989) montrent qu’il existe une multiplicité de sentiers d’équilibre convergeant vers différents équilibres stationnaires à anticipations rationnelles ordonnés en termes de bien-être. Des cycles autoréalisateurs peuvent apparaître dans un environnement d’état stationnaire si les croyances des agents les engendrent. Les anticipations jouent ici un rôle important. La troisième catégorie de modèles est la plus développée et insiste sur la technologie de production, de stockage ou d’intermédiation. Le modèle de Weil (1989) qui s’inspire de celui de Weitzman (1982) démontre l’existence d’une multiplicité d’équilibres à tâches solaires paramétrés par les anticipations (optimistes ou pessimistes) des consommateurs avec une technologie de stockage à rendements croissants. Dans la lignée de ce modèle, Cooper et Corbae (2002) analysent les crises financières en utilisant une technologie d’intermédiation à rendements croissants qui est à l’origine d’équilibres multiples. Dans un modèle à générations imbriquées d’agents, Rivard (1994) utilise aussi une technologie à rendements croissants dans un modèle de concurrence monopolistique pour engendrer l’existence d’équilibres stationnaires Pareto ordonnés. Les équilibres multiples sont ordonnés en termes de bien-être étant donné que les équilibres associés à un investissement élevé dominent ceux associés à un savoir-faire moins élevé. Le modèle suivant fonde les rendements croissants sur la technologie.
4.2 Un modèle d’équilibres de sous-emploi avec rendements croissants et apprentissage
Le modèle à générations imbriquées d’Evans et Honkapohja (1995) se propose d’étudier le rôle joué par les rendements croissants dans la technologie de production dans un contexte de marchés incomplets. L’intérêt essentiel de ce modèle dynamique réside dans la mise en évidence de complémentarités intertemporelles et dans l’analyse de politiques économiques dont les effets sont rendus possibles par un mécanisme d’apprentissage qui explicite la formation des anticipations.
4.2.1 Description de l’économie
Soit une économie de concurrence parfaite à horizon infini dans laquelle existe des générations successives d’individus qui vivent durant deux périodes, des agents vieux et des agents jeunes en nombre égal. À chaque période, les agents jeunes coexistent avec les agents vieux. Il est supposé que les agents d’une même génération sont identiques et que la population est constante dans les deux périodes. Chaque génération réalise des échanges avec celle qui l’a précédée. Il existe un seul bien périssable produit en quantité yt par les agents jeunes et consommé par les agents vieux. Chaque agent jeune produit une quantité de bien et l’échange contre une quantité de monnaie m distribuée en début de période à chaque agent vieux. La monnaie est le seul actif réserve de valeur. Le bien est produit avec la technologie yt = F(nt, Nt), où nt et Nt représentent respectivement la quantité de travail utilisée et l’offre de travail agrégée (effort agrégé). Ainsi, chaque plan de production prend en compte l’effort effectué par les autres. Chacun considère la grandeur Nt comme donnée et dispose d’une information parfaite sur celle-ci. La fonction de production est à rendement factoriel individuel décroissant et à rendement factoriel social croissant. La deuxième propriété signifie que le travail agrégé constitue une externalité positive pour la production individuelle[34]. Avec un nombre constant K d’agents dans chaque génération, on a Nt = Knt.
4.2.1.1 Les rendements croissants dans la production
Le niveau de production atteint par l’agent j est donné par la fonction de production suivante :
Les grandeurs nj et Ij représentent respectivement la quantité de travail offerte par l’agent j et le nombre total d’idées dues aux efforts des autres auxquels cet agent a accès. Ainsi, l’intrant est un travail mental permettant la création d’idées (Romer, 1986; Aghion-Howitt, 1998). Quant à I*, il s’agit d’un seuil à partir duquel les innovations influencent la productivité individuelle. Le nombre d’idées proposées par un agent est proportionnel à son offre de travail. Ainsi nj mesure la contribution de l’idée de l’agent j et l’effort de travail associé. Toutes les idées sont disponibles, mais seule une fraction de l’effort total est accessible à chacun. Le nombre total d’idées transmises est proportionnelle à la grandeur agrégée N. La grandeur Ij est déterminée selon une logique d’appariement. Les agents disposent d’une dotation en temps pour trouver et intégrer les idées des autres. Si λ représente la proportion d’idées transmises dans la période (taux uniforme) et N le nombre d’agents, alors le temps qui s’écoule avant l’arrivée d’une idée est 1 / λN. Si a est le temps nécessaire à un agent pour intégrer une nouvelle idée, le temps nécessaire pour recevoir une nouvelle idée et l’intégrer est donc a + (λN)-1. Le nombre total d’idées perçues par l’agent j qui dispose d’une unité de temps est :
Cette technologie d’appariement est croissante avec le nombre d’agents et est bornée par 1 / a (qui devient sa limite quand le nombre d’agents tend vers l’infini) ce qui signifie qu’il existe une limite à l’influence des rendements croissants sur l’effort agrégé. En utilisant les relations (6) et (7), la fonction de production de l’agent j s’écrit :
4.2.1.2 Comportement optimal des agents
La fonction d’utilité d’un agent né à la période t est de la forme W = U(ct+1) – V(nt), où ct+1 est la consommation lorsque l’agent est vieux et nt l’offre de travail lorsqu’il est jeune. La fonction U est supposée continue, homogène, croissante et strictement quasi concave tandis que V est continue, homogène, croissante et strictement convexe. L’agent jeune choisit son offre de travail nt, sa demande de monnaie mt et sa consommation future ct+1 sous une séquence de deux contraintes budgétaires : (i) pt yt = mt et (ii) pet+1ct+1 = m, où pt et pet+1 sont respectivement le prix du bien à la période t et le prix anticipé du bien produit à la période suivante. On suppose des prévisions parfaites sur les prix, soit pet+1 = pt+1 . Le programme d’un agent jeune s’écrit :
À l’équilibre des marchés du bien et de la monnaie, on a respectivement yt = ct (le bien est périssable et ne peut pas être utilisé comme réserve de valeur) et mt = m. Comme pt yt = pt+1ct+1 et yt = F(nt, Knt), alors la condition d’optimalité s’écrit :
On peut en déduire aisément (voir annexe 2) l’application d’équilibre temporaire qui décrit l’évolution de l’offre de travail dans le temps, soit :
4.2.1.3 Équilibres de sous-emploi, défauts de coordination et rendements croissants
Proposition 4.1Il existe une multiplicité d’équilibres de sous-emploi Pareto ordonnés.
Preuve. La multiplicité se conçoit aisément en spécifiant les fonctions de comportement. Considérons que la fonction d’utilité est la somme de fonctions iso-élastiques, soient ![]() et
et ![]() avec ν > 0 et ε > 0. De plus, si F(n, Kn) = nβ ψ(N), la courbe d’offre de travail est
avec ν > 0 et ε > 0. De plus, si F(n, Kn) = nβ ψ(N), la courbe d’offre de travail est ![]() L’application d’équilibre temporaire Γ(ℜ+ → ℜ+) est continûment différentiable, croissante, avec Γ(0) = 0 et
L’application d’équilibre temporaire Γ(ℜ+ → ℜ+) est continûment différentiable, croissante, avec Γ(0) = 0 et ![]() Comme
Comme ![]() elle possède un nombre impair d’équilibres en plus de l’équilibre autarcique. Le modèle possède ainsi trois équilibres stationnaires de prévision parfaite non triviaux[35] (graphique 3).
elle possède un nombre impair d’équilibres en plus de l’équilibre autarcique. Le modèle possède ainsi trois équilibres stationnaires de prévision parfaite non triviaux[35] (graphique 3).
Graphique 3
Multiplicité d’équilibres stationnaires
Pour des valeurs de l’emploi Knt+1 < I* / (λ(1 – aI*)), le point anguleux, on a Ψ(Knt+1) = AI*γ. Dans ce cas, il n’y a pas d’externalités dans la production. Dans l’intervalle [0, ñ [, Γ est croissante concave, il existe deux équilibres (l’équilibre autarcique et l’équilibre à faible niveau d’emploi nB). Pour des valeurs de nt+1 appartenant à l’intervalle [ñ, nH], il existe deux équilibres. Pour certaines valeurs de nt+1, situées au dessus du point anguleux, Γ est croissante et convexe. Dans ce cas, les rendements croissants agissent. Il existe néanmoins une limite à leur influence. Ainsi, dans l’intervalle [nM, nH], Γ redevient concave. Quatre équilibres sont représentés dans le graphique 3. L’ordonnancement au sens de Pareto est aisé à montrer. Considérons deux équilibres associés à deux niveaux d’emploi, soit nM et nH. Notons WM et WH les niveaux de bien-être associés à chacun d’entre eux. À l’équilibre, le bien-être atteint par chaque agent est mesuré par W(n, Kn) = U[F(n, Kn)] – V(n), où la fonction W(n, Kn) est strictement croissante et concave en n. Si, à l’équilibre, un agent choisit d’offrir la quantité nM et les autres la quantité nH, alors W(nM, KnH) < W(nH, KnH) = WH. De plus, on a WM = W(nM, KnM) ≤ W(nM, KnH) tant que F(n, N) est croissante avec N. Si nH > nM, alors WH > WM. Par conséquent, un accroissement du nombre d’agents dans chaque génération augmente le bien-être. L’existence d’équilibres multiples Pareto ordonnés signifie que l’économie peut demeurer sur un état inférieur[36]. Il est alors utile d’analyser la stabilité des équilibres de prévisions parfaites sous apprentissage.
L’idée est de doter les agents d’une procédure d’apprentissage telle qu’ils se comportent comme des économètres (voir section 1.3). Les agents conjecturent la loi de mouvement des variables endogènes que déterminent leurs choix et utilisent une procédure statistique de révision des anticipations pour l’estimer (Bray, 1982; Marcet et Sargent, 1989; Woodford, 1990 et Evans et Honkapohja, 1994). On suppose que tous les agents utilisent un schéma d’apprentissage adaptatif[37] et que les anticipations ne tiennent pas compte des externalités. Dans ce contexte, le comportement des agents dépend des prix anticipés pet+1. À l’équilibre temporaire, les agents observent pt et yt puis formulent des anticipations sur la valeur de la production future yet+1 ou sur l’emploi futur nt+1 en utilisant le fait que yet+1 = F(net+1, Knet+1). Pour net+1 donnée, la fonction d’équilibre temporaire (10) devient nt = Γ(net+1). Le schéma d’apprentissage adaptatif s’écrit net+1 = net + αt(nt-1 – net) = net + αt(F(net) – net), où 0 < αt ≤ 1 et t = 2, 3, ... . Le paramètre αt représente la séquence des pondérations d’erreurs possibles (la vitesse d’apprentissage), avec ![]() Il s’ensuit le résultat suivant (voir annexe 3).
Il s’ensuit le résultat suivant (voir annexe 3).
Proposition 4.2Si Γ possède trois équilibres à anticipations rationnelles nB, nM et nH, avec Γ′(nB) > 0, Γ′(nH) < 1, et Γ′(nM) > 1, alors pour toute valeur initiale ne2 ∈(0, nM), on a![]() et pour tout ne2 > nM, alors
et pour tout ne2 > nM, alors ![]()
Les équilibres étant stables sous apprentissage adaptatif, il est possible de restreindre à deux le nombre d’équilibres et d’énoncer les résultats de statique comparative afférents à la mise en oeuvre de deux types de politiques économiques : une augmentation des dépenses publiques par création monétaire et une subvention à la production financée par une taxe forfaitaire.
4.2.1.4 Politiques économiques
Dans le cas de la politique budgétaire financée par création monétaire, le gouvernement achète une quantité Gt de bien à chaque période t (une fraction constante de la production) en émettant une quantité de monnaie mst = mst-1 + pt Gt. On a alors F(nt, Nt) = F(nt-1, Nt-1) pt-1 / pt + Gt, où Gt = θF(nt, Nt), avec θ∈≥ 0. Dans ce cas, le taux de croissance de la masse monétaire est constant dans le temps, soit mst / mst-1 = (1 – θ)-1. La courbe d’offre de travail devient :
Une augmentation des dépenses publiques et donc de la quantité de monnaie réduit la productivité du travail. L’effet d’une telle politique est représenté dans le graphique 4. Un choc sur θ déplace la courbe représentative Γ vers le bas (la courbe est tracée pour θ = 0,2). En conséquence, les niveaux d’emploi d’équilibres nL et nH évoluent à la baisse. Pour des accroissements suffisamment grands de θ, les équilibres à haut niveau d’emploi comme nM et nH peuvent disparaître. L’influence des rendements croissants est nulle et seul l’équilibre stationnaire nL subsiste. Une économie initialement située sur un équilibre à faible niveau de chômage peut converger vers un équilibre à haut niveau de chômage comme nA (point A).
Graphique 4
Politiques économiques
Dans le cas d’une politique de subvention à la production, on suppose que le gouvernement applique une subvention proportionnelle st sur le prix du bien financée par une taxe forfaitaire Tt. À chaque période, la contrainte budgétaire de l’État est st pt F(nt, Knt) = Tt. Le prix payé par les agents vieux est (1 – st) pt. Les contraintes budgétaires deviennent (i′) pt F(nt, Nt) – Tt = mt et (ii′) (1 – st+1) pt+1ct+1 = mt. Si la subvention est constante, alors la courbe d’offre devient :
Un accroissement du taux de subvention accroît la productivité du travail. Une augmentation des subventions a donc pour effet d’engendrer un déplacement vers le bas de la courbe d’offre de travail comme en atteste le graphique 4 (pour s = 0,25). Les niveaux d’emploi d’équilibre stationnaire nL et nH peuvent augmenter. Lorsque l’économie est initialement située à l’équilibre bas, un accroissement suffisamment important des subventions peut impliquer une bifurcation car elle conduit à la disparition des équilibres stationnaires nL et nM. Dans ce cas, la dynamique d’apprentissage adaptatif permet de sélectionner l’équilibre haut nB (point B).
Conclusion
Les modèles issus de chacune des approches comportent deux caractéristiques communes. D’abord, les complémentarités stratégiques et les effets de report se combinent si bien que le chômage d’équilibre provient des difficultés rencontrées par des agents rationnels pour se coordonner efficacement dans une économie décentralisée. La décentralisation supprime toute communication des intentions de chacun envers les autres (externalités non internalisées). Ainsi, les agents échangent les quantités désirées même s’ils se coordonnent sur un équilibre Pareto dominé. Ensuite, en raison des complémentarités macroéconomiques, les ajustements de prix et de quantités sont plus complémentaires que substituables. L’intérêt d’intégrer des externalités dans certains modèles macroéconomiques d’équilibre général repose sur l’idée que les ajustements de prix peuvent ne pas être suffisants pour atteindre un équilibre optimal. Dans ces conditions, le chômage d’équilibre n’est pas nécessairement lié à la rigidité des prix et des salaires.
Malgré leur structure analytique commune, chaque modèle propose des causes différentes au chômage d’équilibre. Trois classes de modèles d’équilibre général à prix flexibles correspondant à trois variétés d’externalités ont été présentées : (i) les externalités de demande agrégée liées au degré de concurrence sur les marchés, (ii) les externalités de transaction traitant des conséquences de la réalisation des échanges sur des marchés spatialement séparés et (iii) les externalités dues aux rendements croissants. Ainsi, contrairement à une idée répandue, les rendements croissants ne sont pas nécessaires à l’obtention d’équilibres multiples. Si l’hypothèse de rendements croissants est souvent utilisée pour transformer un modèle de défauts de coopération en modèle de défauts de coordination, les problèmes de communication de la demande agrégée et les modalités de réalisation des transactions sont aussi des sources potentielles d’échecs de coordination.
Les modèles présentés n’ont pas tous la même portée. Les modèles fondés sur une approche intertemporelle sont peut-être plus prometteurs dans la mesure où ils offrent des perspectives pour la dynamique et pour la politique économique. La politique économique pose cependant le problème de la sélection d’un équilibre (Manning, 1990; Franke, 2001). En effet, les modèles de défauts de coordination possèdent des équilibres inefficaces non globalement uniques. La transition d’un équilibre à faible niveau d’emploi vers un équilibre où le chômage est plus faible dépend des conditions initiales et de la dynamique dont les développements demeurent pour le moment à l’état embryonnaire. Il est possible que la solution réside dans la manière dont les agents apprennent la convergence vers un équilibre à haut niveau d’activité et d’emploi. Dans certains travaux très récents, le nombre d’équilibres peut être réduit par une procédure d’apprentissage des anticipations. La voie ouverte par l’apprentissage dynamique semble prometteuse pour la restriction du nombre d’équilibres et la sélection d’un équilibre haut par la politique économique.
Appendices
Annexes
Annexe 1
Ordonnancement des équilibres
Soit deux niveaux d’emploi d’équilibre NL et NH, avec 0 < NL < NH. L’utilité d’un consommateur représentatif est ϕ(N) ≡ U((1 – βY) Y(N)) – c((1 + τ(N)) N). Il faut montrer que ϕ(NL) < ϕ(NH). Soit ![]() le programme d’un planificateur bienveillant. On déduit
le programme d’un planificateur bienveillant. On déduit ![]() qui est la condition nécessaire du premier ordre qui est satisfaite pour t = N tant que N vérifie (5). Donc Φ(N) = ϕ(N). De plus,
qui est la condition nécessaire du premier ordre qui est satisfaite pour t = N tant que N vérifie (5). Donc Φ(N) = ϕ(N). De plus, ![]() On en déduit que ϕ(NL) = Φ(NL) < Φ(NH) = ϕ(NH). Le niveau d’utilité atteint à l’équilibre haut est donc supérieur à celui atteint à l’équilibre bas.
On en déduit que ϕ(NL) = Φ(NL) < Φ(NH) = ϕ(NH). Le niveau d’utilité atteint à l’équilibre haut est donc supérieur à celui atteint à l’équilibre bas.
Annexe 2
Détermination de l’offre intertemporelle de travail
Comme pt yy = mt et yt+1 = ct+1 (équilibre en t + 1), il vient : ![]() La condition d’optimalité (9) devient alors
La condition d’optimalité (9) devient alors ![]() Cette relation est une application qui décrit l’évolution de l’offre de travail nt. Posons
Cette relation est une application qui décrit l’évolution de l’offre de travail nt. Posons ![]() Étant donné que T(nt) est une fonction croissante de nt, il est possible d’exprimer sa réciproque. En posant H(⋅) ≡ T-1(⋅) et G(n) = nU′(n), la condition précédente devient nt = T-1(G(nt+1)). Si l’on note Γ = T-1 º G, la condition d’équilibre est donc donnée par (10).
Étant donné que T(nt) est une fonction croissante de nt, il est possible d’exprimer sa réciproque. En posant H(⋅) ≡ T-1(⋅) et G(n) = nU′(n), la condition précédente devient nt = T-1(G(nt+1)). Si l’on note Γ = T-1 º G, la condition d’équilibre est donc donnée par (10).
Annexe 3
Stabilité des équilibres sous apprentissage
Pour net ∈(nM, nH), on sait que net+1 < F(net) < nH (voir graphique 3). Par conséquent, il existe une suite strictement croissante bornée par nH. Supposons qu’elle converge vers n̂ < nH. Posons d = F(n̂) – n̂ > 0. Pour des valeurs suffisamment grandes net+1 ≥ net + αt, d et pour s ≥ 1, il vient ![]() Pour des valeurs de s suffisamment grandes et comme
Pour des valeurs de s suffisamment grandes et comme ![]() on obtient une contradiction. Donc
on obtient une contradiction. Donc ![]() La convergence pour les points initiaux n > nH et n < nU s’appuie sur le même argument.
La convergence pour les points initiaux n > nH et n < nU s’appuie sur le même argument.
Remerciements
Ce texte a été initialement présenté au séminaire IRES de l’Université Catholique de Louvain. Je remercie M. De Vroey et J. Drèze pour leurs commentaires sur une première version de ce texte. Je remercie également le rapporteur anonyme pour ses commentaires et suggestions qui ont permis une amélioration sensible du texte et demeure seul responsable des insuffisances qui subsistent.
Notes
-
[1]
La distinction entre défauts de coordination et défauts de coopération est due à Silvestre (1993).
-
[2]
On se restreindra ici aux seuls équilibres en stratégies pures. Il existe aussi un équilibre en stratégie mixte où chaque entreprise choisit (NE,NE) avec la probabilité 1/3.
-
[3]
Voir Bulow, Geanakoplos et Klemperer (1985). Vives (1990) généralise ce concept avec les jeux supermodulaires.
-
[4]
Une condition suffisante de multiplicité d’équilibres est ∂ϕ / ∂zA(zA) > 1 à un point d’équilibre.
-
[5]
Dans le cas où l’équilibre de Nash symétrique est unique, les complémentarités stratégiques sont une condition nécessaire et suffisante de leur existence (Cooper, 1999).
-
[6]
Voir Heller (1986) et Solow (1986) et Brock-Durlauf (2001). Le modèle analysé dans la section 4 en donne un exemple.
-
[7]
La multiplicité d’équilibres de Nash n’entretient ici aucun lien avec l’information incomplète qui est ici proscrite car les équilibres sont réguliers (l’ensemble des stratégies pures ne se modifie pas suite à une perturbation exogène sur les gains).
-
[8]
Si, par exemple, l’économie est bloquée à un équilibre avec un fort taux de chômage à la période précédente, alors, lorsque les caractéristiques fondamentales de l’économie changent, le nouvel équilibre sera localement proche du précédent. Les conjectures des agents sur les actions choisies par les autres présentent une certaine inertie (mouvement lent) de telle sorte que l’équilibre atteint dans la période suivante est proche de l’ancien. Pour une théorie de la sélection fondée sur l’opinion moyenne, voir Battalio, Beil, Van Huyck (1991). Pour des résultats expérimentaux sur des procédures de sélection dans des jeux de coordination, voir Cooper, DeJong, Forsythe, Ross (1990).
-
[9]
Il existe trois types d’apprentissage. Le premier est l’apprentissage rationnel dans lequel les agents connaissent la structure du modèle et utilisent des procédures de révision des anticipations fondés sur des croyances bayésiennes. Le deuxième est l’apprentissage éductif (Guesnerie, 1992) qui décrit un processus de tâtonnement mental. Le troisième est l’apprentissage adaptatif qui peut prendre trois formes. La première concerne des économies déterministes et généralise les anticipations adaptatives (Grandmont, 1998). La seconde, qui est l’approche évoquée ici, s’applique à des modèles déterministes et stochastiques et consiste à considérer que les agents agissent comme des économètres (Evans et Honkapohja, 1994). Cette méthode sera utilisée dans un modèle dynamique (section 4). Enfin, la troisième repose sur l’intelligence artificielle qui apparente les agents à des systèmes artificiels qui répondent à des sollicitations externes (Arifovic, 1994; Cho et Sargent, 1996).
-
[10]
Un équilibre à anticipations rationnelles est E-stable si et seulement si toutes les valeurs propres de la matrice jacobienne de l’application qui relie la loi dynamique perçue à la loi dynamique courante ont leurs parties réelles inférieures à l’unité.
-
[11]
L’absence d’une parabole alternative à la théorie de l’équilibre général concurrentiel a motivé cette première approche. Elle fut initialement une tentative pour réhabiliter l’idée de demande effective keynésienne dans une perspective walrasienne. Les premières contributions sont de Patinkin (1956), Clower (1965) et Leijonhufvud (1973). Cette lignée conduit à la théorie des équilibres à prix fixes de Barro-Grossman (1971) développée par Drèze (1975) et Bénassy (1993). Les interactions entre marchés relèvent principalement des quantités traduisant, selon le régime considéré, l’existence de contraintes d’offre ou de demande perçues par les agents. Malgré leur intérêt, le résultat d’existence du chômage d’équilibre est trop dépendant de l’hypothèse de prix et salaires rigides, confortant ainsi la proposition classique selon laquelle en régime concurrentiel stable, la flexibilité des prix et des salaires permet à l’économie de se diriger vers un régime de plein emploi. Comme Patinkin (1956) l’avait pressenti, le chômage (involontaire) ne serait alors qu’un phénomène temporaire de déséquilibre qui disparaîtrait après le processus d’ajustement des prix.
-
[12]
Une telle propriété est conservée par agrégation même si les fonctions de demande agrégées pour chaque bien peuvent être croissantes en raison des effets revenus.
-
[13]
Elle peut signifier que les agents ne consomment pas le bien produit par l’entreprise dans laquelle ils travaillent.
-
[14]
Voir Silvestre (1993) pour une présentation du modèle de Hart (1982). Le modèle de prospection avec externalité de demande agrégée de Drazen (1987b) insiste sur les effets de report entre marchés.
-
[15]
Les complémentarités stratégiques et les effets de report entre secteurs sont obtenus en limitant les valeurs prises par les élasticités de demande et par le taux marginal de substitution entre le loisir et les biens produits.
-
[16]
Le modèle de Kiyotaki (1988), qui est une extension de celui de Blanchard-Kiyotaki (1987), montre que l’existence d’équilibres multiples est due aux rendements croissants. Les équilibres associés aux croyances optimistes dominent les équilibres associés aux croyances pessimistes. Dans le modèle de Weitzman (1982), les situations d’équilibres de sous-emploi sont liées à un problème de communication de demande qui justifie des dépenses faibles. Solow (1986) présente un modèle similaire en insistant sur les effets multiplicateurs. Pagano (1990) combine les deux modèles précédents.
-
[17]
Une telle hypothèse permet d’éviter de rendre compte des modalités de répartition des profits ainsi que ses effets sur la détermination du niveau de l’activité. Selon Heller (1986), la distribution des profits est une source d’échecs de coordination. Cette hypothèse permet aussi d’obtenir un continuum d’équilibres dépendant du niveau de la demande.
-
[18]
Un équilibre de l’économie fonctionnant sous les hypothèses précédentes est un équilibre de Nash parfait en sous-jeu. Cette définition de l’équilibre est fondée sur une rationalité séquentielle. Le concept d’équilibre parfait en sous-jeux induit par l’environnement et les institutions de ce modèle est tel que chaque agent perçoit correctement qu’il ne peut tirer avantage d’un quelconque changement unilatéral de stratégie compte tenu des actions et réactions des autres.
-
[19]
Le niveau de chômage involontaire varie avec (n – k). Notons que de tels agents sont en équilibre autarcique.
-
[20]
Si les chômeurs prennent l’initiative de proposer un salaire plus faible, les consommateurs non rationnés peuvent proposer d’abaisser leur salaire. Un processus à la Bertrand peut alors se déclencher ce qui ne favoriserait aucun agent.
-
[21]
Drèze (1997) analyse la macroéconomie du modèle de Roberts avec des prix fixes et des rationnements sur les offres.
-
[22]
Jones et Manuelli (1992) considèrent une version à quatre étapes de ce modèle. Au début du jeu, les entreprises fixent les prix et les salaires. Ensuite, les consommateurs annoncent les quantités de travail qu’ils désirent vendre. Compte tenu de cette information sur les offres, les firmes achètent les quantités de travail et déterminent les quantités produites. Enfin, dans une quatrième étape, les consommateurs achètent les biens produits. Chez Roberts (1987) la dernière étape est incluse dans la deuxième (simultanéité des actions). Ceci explique que la situation autarcique soit un équilibre. Jones et Manuelli montrent qu’une économie décentralisée avec obligation de coordination par l’échange ne conduit pas nécessairement à l’équilibre keynésien. Ce résultat est néanmoins limité car il repose sur une modification importante dans la structure du jeu.
-
[23]
Les modalités de détermination des coûts diffèrent selon les modèles. Voir Chatterjee (1988) ou Pagano (1989).
-
[24]
Dans ces modèles, l’incitation à participer des agents aux activités du marché dépend du nombre d’échanges. Dans une perspective semblable, Chatterjee (1988) montre qu’une externalité associée au nombre d’agents apparaît dans les économies où existe de l’incertitude dont le degré dépend du niveau de participation des agents. L’entrée sur les marchés de nouveaux agents réduit l’incertitude liée à la participation des autres agents.
-
[25]
Les complémentarités stratégiques sont liées au fait que si tous les agents sauf un décident un coût critique de production plus élevé, alors le nombre de projets de production et d’échanges augmentent ce qui justifie que le dernier agent choisisse un coût de production critique plus élevé. L’utilité anticipée associée au fait de produire augmente lorsqu’un plus grand nombre d’agents mettent en oeuvre des projets de production (effets de report positifs) et diminue dans le cas contraire (effets de report négatifs). Le gain s’élève donc avec le niveau d’activité. Les effets de rétroaction sur la décision de production expliquent la multiplicité d’équilibres tandis que les externalités sont à l’origine du fait que de tels équilibres sont localement inefficaces. Dans ces modèles, le chômage est défini comme le temps nécessaire pour produire un bien.
-
[26]
Diamond et Fudenberg (1989) proposent une extension dynamique de ce modèle et montrent l’existence d’une multiplicité de trajectoires dynamiques qui convergent vers différents équilibres stationnaires à anticipations rationnelles ordonnés en termes de bien-être. Des cycles endogènes autoréalisateurs peuvent apparaître si les agents les conjecturent.
-
[27]
Les modèles de prospection monétaire dans la lignée de Kiyotaki et Wright (1993) évitent ces écueils dans la mesure où ils posent explicitement les problèmes de la coïncidence réciproque des besoins et celui de l’acceptation de la monnaie.
-
[28]
La forme des courbes d’offre et de demande de travail fait apparaître des zones de complémentarités stratégiques et des effets de report positifs. Ainsi, lorsque les agents font un effort élevé, le gain marginal de chacun augmente avec l’effort. Par exemple, si les entreprises consentent des efforts de vente importants, le coût d’achat du bien diminue de sorte que l’augmentation de l’utilité marginale de la consommation compensera l’accroissement de la désutilité marginale du travail. Tous les consommateurs auront donc intérêt à augmenter leur consommation (équilibres multiples). De plus, il existe des effets de report positifs. Ainsi, à l’équilibre bas, l’utilité des consommateurs, évaluée le long de la fonction d’offre de travail (les profits des entreprises, évalués le long de la demande de travail) augmentent avec les efforts de vente des entreprises (les efforts de vente des consommateurs) ce qui diminue les coûts d’achat du travail (le coût d’achat du bien) et augmente l’emploi (la consommation). De tels équilibres sont donc Pareto ordonnés.
-
[29]
Les modèles issus de cette lignée soulignent les effets de la participation des firmes sur les marchés. Dans un modèle de cycle réel, Howitt (1988) s’intéresse aux échanges d’un bien sur des îles à la Phelps-Lucas. Les services du travail sont échangés sur chaque île moyennant des coûts de recherche et de recrutement. Lorsque le nombre de firmes augmente, les coûts de l’échange diminuent (externalité d’échange positive). Le modèle produit une multiplicité d’équilibres de sous-emploi Pareto dominés. Dans un modèle de cycle d’affaires à anticipations rationnelles, Howitt et McAfee (1992) considèrent l’interaction entre les coûts de transaction et les esprits animaux des agents qui constituent une variable aléatoire exogène. Selon l’état des anticipations, le sentier d’emploi agrégé emprunte aléatoirement une trajectoire optimiste quand les firmes embauchent ou une trajectoire pessimiste quand elles recrutent peu. Les vagues d’optimisme ou de pessimisme autoréalisantes sont dues à la présence d’externalités liées aux coûts de transaction qui dépendent du nombre de firmes présentes sur les marchés. La production est d’autant plus rentable et l’emploi élevé que la production des entreprises augmente.
-
[30]
En ce sens, le chômage d’équilibre est involontaire. À l’équilibre bas, la situation avec chômage diffère néanmoins de l’acception keynésienne selon laquelle le niveau de l’emploi se fixe sur la demande de travail des entreprises. On peut notamment faire référence au chapitre 2 de la Théorie Générale de Keynes dans lequel le chômage involontaire définit une situation dans laquelle la volonté de participation des salariés au marché du travail trouve une limite dans la demande de travail des entreprises (rejet du second des deux postulats de l’économie classique). Le chômage involontaire d’équilibre défini de la sorte n’a jamais été démontré dans un modèle de concurrence parfaite à prix et salaires flexibles.
-
[31]
Ce problème concerne toute économie walrassienne décentralisée sans monnaie. En l’absence d’une chambre de compensation (système de comptes centralisé), les agents ne peuvent pas obtenir leur allocation individuelle désirée (voir Ostroy et Starr, 1974). L’origine de ce problème réside dans le blocage de l’échange par le troc direct ou indirect.
-
[32]
L’approche de prospection monétaire de Kiyotaki et Wright (1993) issue de celle de Diamond (1984) peut être utilisée pour traiter des conséquences de la réalisation décentralisée des transactions sur la détermination du niveau de l’activité et de l’emploi. Cependant, les modèles issus de cette lignée rencontrent quatre limites. D’abord, et contrairement au modèle de Diamond, cette approche ne fournit aucune proposition de politique économique. Ensuite, elle ne permet pas de traiter des rationnements étant donné que l’organisation des marchés est passée sous silence. Ensuite, la plupart des modèles relèvent de l’interaction stratégique ou de l’approche en équilibre partiel ce qui restreint la dimension du problème posé. Enfin, le seul type de chômage envisageable est le chômage naturel dont le niveau peut varier avec la quantité de monnaie. La cause du chômage est une quantité insuffisante de monnaie qui restreint le nombre d’échanges réalisables.
-
[33]
Notons que le problème de la transition d’un équilibre bas vers un équilibre haut est aussi passé sous silence.
-
[34]
Les firmes bénéficient donc d’une externalité positive provenant de la quantité agrégée de travail. Chaque entreprise tire ainsi profit du niveau de développement de l’économie. La quantité de travail agrégée représenterait ainsi le stock de connaissances acquises par les agents. Plus l’économie est développée et plus ce stock est important, ce qui entraîne une productivité supérieure du travail privé. En d’autres termes, plus le nombre d’agents est élevé (plus la taille du marché est grande), et plus l’entreprise a intérêt à augmenter sa production.
-
[35]
L’équilibre trivial est l’équilibre autarcique. La courbe de le graphique 3 est tracée pour les valeurs suivantes des paramètres : A = 1, ε = 0,2, ν = 0,41, a = 0,2, β = 0,2, γ = 4,8, λ = 0,01, K = 200 et I* = 2.
-
[36]
Dans ce modèle, le chômage peut être défini comme le temps nécessaire aux agents pour comprendre et intégrer une connaissance pour produire. En l’absence de rendements croissants, les idées nouvelles sont rares et toutes les opportunités de production ne sont pas exploitées à l’équilibre. De nouvelles rencontres ont alors des effets positifs sur le niveau de l’emploi. En régime de rendements croissants, les nouvelles idées sont disponibles plus rapidement de telle sorte que les agents se coordonnent sur un équilibre à plus haut niveau d’activité et d’emploi (le chômage baisse).
-
[37]
L’algorithme d’apprentissage adaptatif signifie que les agents agissent comme si l’économie était à l’équilibre tout en estimant la vraie valeur de l’offre de travail en utilisant une moyenne pondérée des valeurs passées.
Bibliographie
- Aghion, P. et P. Howitt (1998), Endogenous Growth Theory, MIT Press.
- Arifovic, J. (1994), « Genetic Algorithm Learning and the Cobweb Model », Journal of Economic Dynamics and Control, 18 : 3-28.
- Azariadis, C. (1983), « Employment with Asymmetric Information », Quarterly Journal of Economics, 98 : 157-172.
- Baily, M. (1974), « Wages and Employment under Uncertain Demand », Review of Economic Studies, 41 : 37-50.
- Ball, L. et D. Romer (1991), « Sticky Prices as Coordination Failure », American Economic Review, 81 : 539-552.
- Barro, R. et S. Grossman (1971), « A General Disequilibrium Model of Income and Employment », American Economic Review, 6 : 82-93.
- Battalio, R., R. Beil et J. Van Huyck (1991), « Strategic Uncertainty, Equilibrium Selection, and Coordination Failure in Average Opinion Games », Quarterly Journal of Economics, 106 : 885-911.
- Bénassy, J.P. (1993), « Nonclearing Markets: Microeconomic Concepts and Macroeconomic Applications », Journal of Economic Literature, 31 : 732-761.
- Blanchard, J.O. et N. Kiyotaki (1987), « Monopolistic Competition and the Effects of Aggregate Demand », American Economic Review, 4 : 647-666.
- Bray, M. (1982), « Learning, Estimation and Stability of Rational Expectations Equilibria », Journal of Economic Theory, 26 : 318-339.
- Brock, W. et S. Durlauf (2001), « Discrete Choice with Social Interactions », Review of Economic Studies, 68 : 235-260.
- Bryant, J. (1987), « The Paradox of Thrift, Liquidity Preference and Animal Spirits », Econometrica, 55 : 1 231-1 235.
- Bryant, J. (1983), « A Simple Rational Expectations Keynesian-type Model », Quarterly Journal of Economics, 98 : 525-528.
- Bulow, J., J. Geanakoplos et P. Klemperer (1985), « Multimarket Oligopoly: Strategic Substitutes and Complements », Journal of Political Economy, 93 : 448-511.
- Chatterjee, S. (1988), « Participation Externality as a Source of Coordination Failure in a Competitive Economy», mimeo, University of Iowa.
- Chatterjee, S. et R. Cooper (1989), « Multiplicity of Equilibria and Fluctuations in Dynamic Imperfectly Competitive Economies », American Economic Review, 79 : 353-357.
- Chatterjee, S., R. Cooper, et B. Ravikumar (1993), « Strategic Complementarity in Business Formation: Aggregate Fluctuations and Sunspot Equilibria », Review of Economic Studies, 60 : 795-811.
- Cho, I. et T. Sargent (1996), « Neural Networks and for Encoding and Adapting in Dynamic Economies », in H. Amman, D. Kendrick et J. Rust (éds), Handbook of Computational Economics, Elsevier, vol. 1, p. 441-470.
- Clower, R. (1965), « The Keynesian Counter-Revolution: A Theoretical Appraisal », in F. Hahn et F. Brechling (éds), The Theory Of Interest Rates, Macmillan, p. 270-297.
- Clower, R. et A. Leijonhufvud (1975), « The Coordination of Economic Activities », American Economic Review, 65 : 182-188.
- Cooper, R. (1994), « Equilibrium Selection in Imperfectly Competitive Economy with Multiple Equilibria », Economic Journal, 104 : 1 106-1 122.
- Cooper, R. (1999), Coordination Games: Complementarities and Macroeconomics, CUP, Cambridge.
- Cooper, R. et D. Corbae (2002), « Financial Collapse: A Lesson from the Great Depression », Journal of Economic Theory, 107 : 159-190.
- Cooper, R., D. Dejong, R. Forsythe et T. Ross (1990), « Selection Criteria in Coordination Games: Some Experimental Results », American Economic Review, 80 : 218-233.
- Cooper, R., D. Dejong, R. Forsythe et T. Ross (1992), « Communication in Coordination Games », Quarterly Journal of Economics, 107 : 739-771.
- Cooper, R. et A. John (1988), « Coordinating Coordination Failures in Keynesian Models », Quarterly Journal of Economics, 103 : 441-463.
- De Canio, S. (1979), « Rational Expectations and Learning from Experience », Quarterly Journal of Economics, 94 : 47-57.
- Diamond, P. (1981), « Mobility Costs, Frictional Unemployment, and Efficiency », Journal of Political Economy, 89 : 789-812.
- Diamond, P. (1982), « Aggregate Demand Management in Search Equilibrium », Journal of Political Economy, 90 : 881-894.
- Diamond, P. (1984), « Money in Search Equilibrium », Econometrica, 52 : 1-20.
- Diamond, P. (1987), « Equilibrium Without an Auctioneer », in T. Bailey (éd.), Advances in Economic Theory, CUP : 363-378.
- Diamond, P. et D. Fudenberg (1989), « Rational Expectations Business Cycles in Search Equilibrium », Journal of Political Economy, 97 : 606-619.
- Drazen, A. (1987a), « Reciprocal Externalities Models of Low Employment », European Economic Review, 31 : 436-443.
- Drazen, A. (1987b), « Involuntary Unemployment and Aggregate Demand Spillovers in an Optimal Search Model », Working Paper, Hebrew University of Jerusalem.
- Drèze, J. (1975), « Existence of an Equilibrium under Price Rigidity and Quantity Rationing », International Economic Review, 16 : 301-320.
- Drèze, J. (1997), « Walras-Keynes Equilibria Coordination and Macroeconomics », European Economic Review, 41 : 1 735-1 762.
- Durlauf, S. (1991), « Multiple Equilibria and Persistence in Aggregate Fluctuations », American Economic Review, 81 : 70-74.
- Evans, G. et S. Honkapohja (1994), « On the Local Stability of Sunspot Equilibria under Adaptative Learning Rules », Journal of Economic Theory, 64 : 142-161.
- Evans, G. et S. Honkapohja (1995), « Increasing Social Returns, Learning and Bifurcation Phenomena », in A. Kirman et M. Salmon (éds), Learning and Rationality in Economics, p. 102-126.
- Evans, G. et S. Honkapohja (1999), « Learning Dynamics », in J. Taylor et M. Woodford (éds), Handbook of Macroeconomics, Elsevier, Amsterdam : North-Holland, vol. 1, p. 449-542.
- Evans, G. et S. Honkapohja (2001), Learning and Expectations in Macroeconomics, Princeton University Press, Princeton.
- Franke, R. (2001), « Equilibrium Selection under Cyclical Disequilibrium Dynamics », Oxford Economic Papers, 53 : 166-186.
- Gordon, R. (1974), « A Neo-classical Theory of Keynesian Unemployment », Economic Inquiry, 19 : 431-459.
- Grandmont, J.M. (1998), « Expectations Formation and Stability of Large Socioeconomics Systems », Econometrica, 66 : 741-781.
- Guesnerie, R. (1992), « An Exploration of the Eductive Justifications of the Rational-expectations Hypothesis », American Economic Review, 82 : 1 254-1 278.
- Hart, O. (1982), « A Model of Imperfect Competition with Keynesian Features », Quarterly Journal of Economics, 97 : 109-138.
- Heller, W. (1986), « Coordination Failure under Complete Markets with Applications to Effective Demand », in W. Heller et R. Starr (éds), Equilibrium Analysis: Essays in Honor of K.J. Arrow, vol. 2 : 155-175.
- Horstein, A. (1993), « Monopolistic Competition, Increasing Returns to Scale and the Importance of Productivity Shocks », Journal of Monetary Economics, 31 : 299-316.
- Howitt, P. (1985), « Transactions Costs in the Theory of Unemployment », American Economic Review, 75 : 88-100.
- Howitt, P. (1988), « Business Cycles with Costly Search and Recruiting », Quarterly Journal of Economics, 103 : 177-165.
- Howitt, P. (1990), The Keynesian Recovery, Philip Alan, New-York.
- Howitt, P. et R. McAfee (1987), « Costly Search and Recruiting », International Economic Review, 28 : 89-107.
- Howitt, P. et R. McAfee (1992), « Animal Spirits », American Economic Review, 82 : 493-507.
- Jones, L. et R. Manuelli (1992), « The Coordination Problem and Equilibrium Theories of Recessions », American Economic Review, 82 : 451-471.
- Kiyotaki, N. (1988), « Multiple Expectational Equilibria under Monopolistic Competition », Quarterly Journal of Economics, 103 : 695-713.
- Kiyotaki, N. et R. Wright (1993), « A Search-theoretic Approach to Monetary Economics, American Economic Review, 83 : 63-77.
- Leijonhufvud, A. (1973), « Effective Demand Failures », Swedish Journal of Economics, 75 : 27-58.
- Lucas, R. (1986), « Adaptative Behaviour and Economic Theory », Journal of Business, 59 : S401-S426.
- Lucas, R. (1987), Models of Business Cycles, Basil Blackwell.
- Manning, A. (1990), « Imperfect Competition, Multiple Equilibria and Unemployment Policy », Economic Journal, 100 : 151-162.
- Marcet, A. et T. Sargent (1989), « Convergence of Least Squares Learning Mechanisms in Self-referential Stochastic Models », Journal of Economic Theory, 48 : 337-368.
- Mortensen, D. (1986), « Job Search and Labor Market Analysis », in O. Ashenfelter et R. Layard (éds) Handbook of Labor Economics, Elsevier, Amsterdam : North Holland, vol. 2, p. 849-919.
- Ostroy, J. et R. Starr (1974), « Money and the Decentralization of Exchange », Econometrica, 42 : 1 093-1 113.
- Pagano, M. (1989a), « Trading Volume and Asset Liquidity », Quarterly Journal of Economics, 104 : 255-274.
- Pagano, M. (1989b), « Endogenous Market Thinness and Stock Market Volatility », Review of Economic Studies, 56 : 269-288.
- Pagano, M. (1990), « Imperfect Competition, Underemployment Equilibria and Fiscal Policy », Economic Journal, 100 : 440-463.
- Patinkin, D. (1956), Money, Interest and Prices, Harper and Row.
- Pissarides, C. (2000), Equilibrium Unemployment Theory, 2e edition, Basil Blackwell, Oxford.
- Rivard, B. (1994), « Monopolistic Competition, Increasing Returns, and Self-fulfilling Propheties », Journal of Economic Theory, 62 : 346-362.
- Roberts, J. (1987), « An Equilibrium Model with Involuntary Unemployment at Flexible, Competitive Prices and Wages », American Economic Review, 77 : 856-874.
- Romer, P. (1986), « Increasing Returns and Long Run Growth », Journal of Political Economy, 94 : 1 002-1 037.
- Shapiro, C. et J. Stiglitz (1984), « Equilibrium Unemployment as a Worker Discipline Device, American Economic Review, 74 : 433-444.
- Silvestre, J. (1993), « The Market Power Foundations of Macroeconomic Policy », Journal of Economic Literature, 31 : 105-141.
- Solow, R. (1986), « Monopolistic Competition and the Multiplier », in H. Heller et R. Starr (éds), Equilibrium Analysis: Essays in Honor of K.J. Arrow, Vol. 2 : 301-315.
- Startz, R. (1989), « Monopolistic Competition as Foundation for Keynesian Macroeconomic Models », Quarterly Journal of Economics, 104 : 737-752.
- Vives, X. (1990), « Nash Equilibrium with Strategic Complementarities », Journal of Mathematical Economics, 19 : 305-321.
- Weil, P. (1989), « Increasing Returns and Animal Spirits », American Economic Review, 79 : 889-894.
- Weiss, A. (1991), Efficiency Wages Models of Unemployment, Layoffs, and Wages Dispersions, Clarendon Press, Oxford.
- Weitzman, M. (1982), « Increasing Returns and the Foundations of Unemployment Theory », Economic Journal, 92 : 787-804.
- Woodford, M. (1990), « Learning to Believe in Sunspots », Econometrica, 58 : 277-307.
List of figures
Jeux I : défaut de coopération
Jeux II : défaut de coordination
Graphique 1
Multiplicité d’équilibres et défauts de coordination
Graphique 2
Équilibres multiples et coûts de transaction
Graphique 3
Multiplicité d’équilibres stationnaires
Graphique 4
Politiques économiques