Article body
Introduction
Depuis Knight (1921), il est d’usage de considérer que lorsque les probabilités associées aux différents états de la nature sont inconnues, le décideur (l’agent économique) se trouve en situation d’incertitude, par opposition au risque où elles sont connues. Dans ce cadre, l’approche traditionnelle en analyse économique suppose que le décideur rationnel assigne des probabilités subjectives aux évènements et se comporte suivant une règle d’utilité espérée (Savage, 1954). L’intérêt de cette représentation du choix présence d’incertitude est double. En premier lieu, la théorie de l’utilité espérée assure la cohérence des méthodes et concepts de l’analyse économique entre les décisions en présence de risque et les décisions prises en présence d’incertitude. Le choix individuel face à un environnement relativement complexe et inconnu se réduit à l’emploi d’une règle de décision de type moyenne pondérée. Une règle de décision aussi simple peut facilement être employée dans la modélisation en économie appliquée pour intégrer l’incertitude inhérente à l’environnement décisionnel des agents économiques. Dans le prolongement de von Neumann et Morgenstern (1944), la fonction d’utilité permet de prendre en compte le goût ou l’aversion pour le risque de l’agent économique et les probabilités subjectives mesurent les croyances que cet agent assigne aux différents évènements. Il n’y a donc pas de différence entre le risque et l’incertain, puisque tous deux utilisent les mêmes objets – des probabilités et des utilités – et la même règle de prise de décision. Le second intérêt de cette représentation est la simplicité des objets qu’elle manipule. Toute source d’incertitude peut ainsi être appréhendée simplement par une distribution de probabilités subjectives, guidant les décisions de l’agent économique (Cyert et DeGroot, 1974). De plus, dans une perspective dynamique, toute nouvelle information pertinente sur la vraisemblance des évènements est intégrée de manière cohérente par l’agent économique qui révise alors les probabilités suivant la règle de Bayes. La théorie de l’utilité espérée fournit ainsi non seulement un cadre conceptuel élégant et unifié mais également un ensemble d’outils complémentaires adaptés à tout type d’analyse économique.
Parallèlement au développement de son cadre formel, la théorie de l’utilité espérée a été constamment et largement critiquée. Elle a d’abord été critiquée pour les limites inhérentes à ses hypothèses, notamment l’axiome d’indépendance (Allais, 1953), puis pour l’irréalisme de ses prédictions dans un cadre statique (Ellsberg, 1961) ou dynamique (Lichtenstein et al., 1982) et finalement pour sa difficulté à rendre compte des comportements joints de prise de risque et d’assurance (Friedman et Savage, 1948). Dans ces remises en cause, les travaux d’Ellsberg (1961) occupent une place centrale. Cette place n’est pas tellement liée à la remise en cause de l’utilité espérée en soi. En effet, le fait que la théorie de l’utilité espérée ne permette pas de décrire de manière satisfaisante le comportement individuel est déjà contenu dans le paradoxe d’Allais, renforcé par les célèbres travaux de Kahneman et Tversky (1979). C’est donc sur un tout autre plan que la critique suscitée par Ellsberg se porte, celui de l’emploi d’une distribution de probabilités subjectives ou d’un comportement identique face à l’incertain et au risque.
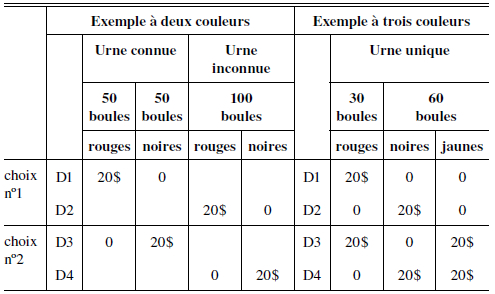
Ellsberg propose, entre autres, deux exemples très simples : l’un impliquant deux urnes remplies de boules de deux couleurs différentes (appelé exemple ou paradoxe à deux couleurs) et l’autre impliquant une seule urne, mais remplies de boules de trois couleurs différences (appelé exemple ou paradoxe à trois couleurs). Dans l’exemple à deux couleurs, le décideur fait face à deux urnes comprenant chacune 100 boules. Dans la première urne se trouvent 50 boules noires et 50 boules rouges. La composition de la seconde urne est inconnue. Le décideur fait face à un choix entre deux options. Dans la première option, une boule sera tirée au hasard dans l’urne que le décideur aura désignée. Si la boule tirée est rouge, le décideur gagne 20 $. Le décideur doit donc prendre une décision, à savoir choisir une urne sur laquelle parier (décision D1 s’il choisit de parier sur l’urne connue et décision D2 s’il choisit de parier sur l’urne inconnue). Dans la deuxième option, une boule sera tirée au hasard dans l’urne que le décideur aura désignée et si la boule tirée est noire, le décideur gagne 20 $. Le décideur doit donc prendre une décision, à savoir choisir une urne sur laquelle parier (décision D3 s’il choisit de parier sur l’urne connue, décision D4 s’il choisit de parier sur l’urne inconnue). Depuis les travaux de Becker et Brownson (1964), plusieurs d’études expérimentales suggèrent que la plupart des individus choisissent les décisions D1 et D3 plutôt que les décisions D2 et D4. Ainsi, ces décideurs agissent comme s’il y avait plus de chances de tirer une boule rouge dans l’urne connue que dans l’urne inconnue, mais également comme s’il y avait plus de chances de tirer une boule noire dans l’urne connue que dans l’urne inconnue.
Tableau 1
Les paiements dans les exemples d’Ellsberg (1961)
Dans l’exemple à trois couleurs, le décideur fait face à une seule urne contenant 90 boules pouvant être de trois couleurs différentes : 30 boules sont rouges et les 60 boules restantes peuvent être noires ou jaunes, dans une proportion inconnue. Une boule sera tirée au hasard dans l’urne. Tout d’abord, le décideur a le choix entre une décision lui procurant 20 $ si la boule tirée est rouge (et rien sinon) et une décision lui procurant 20 $ si la boule tirée est noire. Le choix est donc entre une décision D1 avec une probabilité connue de 1/3 d’obtenir 20 $ et une décision D2 avec une probabilité inconnue d’obtenir la même conséquence. Le second choix est construit sur la base de D1 et, en ajoutant 20 $ dans les deux décisions (D3 et D4) au cas où la boule tirée est jaune. La plupart des individus choisissent les décisions D1 et D4. Ils agissent donc comme s’il y avait moins de boules noires que de boules jaunes en préférant D1 mais ensuite comme s’il y avait plus de boules noires que de boules jaunes en préférant D4.
L’importance des travaux d’Ellsberg (1961) repose sur une remise en cause fondamentale de l’approche traditionnelle de la décision individuelle, à savoir l’hypothèse selon laquelle les individus se comportent « comme s’ils » utilisaient des probabilités subjectives et qu’ils traitaient ces probabilités exactement comme ils traitent des probabilités objectives. Les exemples de choix imaginés par Ellsberg montrent que les individus n’ont pas uniquement de l’aversion pour le risque, mais également pour l’ambiguïté, c’est-à-dire face à l’incertitude sur les probabilités. En particulier, les individus réagissent fortement à l’absence d’une information qui pourrait être disponible. Selon Ellsberg, l’ambiguïté d’une information se définit comme « the quality depending on the amount, type, reliability, and ’unanimity’ of information giving rise to one’s ’degree of confidence’ in an estimate of relative likelihoods »[1].
Bien que fondés sur des exemples simples, construits à partir de tirages de boules dans des urnes, les exemples d’Ellsberg montrent qu’il existe une incertitude sur l’incertitude, et que cette dernière n’est pas prise en compte par la théorie de l’utilité espérée alors qu’elle constitue un déterminant majeur des choix individuels. En effet, la théorie de l’utilité espérée ne permet pas au décideur d’avoir une confiance plus ou moins limitée dans ses croyances. Dès lors que, a contrario, on permet au décideur de ne pas avoir une confiance illimitée dans ses croyances, l’aversion à l’ambiguïté qui en résulte conduit à un effritement du modèle d’utilité espérée.
Suite à cette remise en cause fondamentale, les trente dernières années ont vu naître de nombreuses alternatives théoriques à l’utilité espérée que nous regrouperons toutes sous l’appellation « modèles d’ambiguïté ». D’ailleurs, suite à ces travaux, le terme « ambiguïté » est souvent utilisé comme synonyme d’incertitude non probabiliste (Wakker, 2010). Dans cet article, nous proposons un panorama de cette littérature, de ses apports théoriques, des mesures empiriques réalisées et de l’intérêt de cette littérature pour l’analyse économique. Pour des raisons de concision, certains éléments ne seront pas abordés. Ainsi, la définition théorique de l’aversion à l’ambiguïté et la question de la dynamique des croyances seront laissées de côté pour se concentrer sur l’exposition des modèles d’ambiguïté. Sur ces points, le lecteur peut cependant consulter les analyses proposées par Etner et al. (2012), Machina et Sinischalchi (2014) ou Gilboa et Marinacci (2013). De même, l’article de Jeleva (2014), publié dans ce numéro, est complémentaire à notre panorama et montre l’intérêt des modèles d’ambiguïté pour mettre à jour de nouveaux mécanismes mis en oeuvre dans les décisions financières et le fonctionnement des marchés financiers.
Le plan de notre article est le suivant : la section 1 présente les principaux modèles d’ambiguïté ainsi que leurs représentations; la section 2 présente les principaux résultats empiriques concernant ces modèles et la dernière partie conclut.
1. La décision en l’ambiguïté : évaluation des décisions
1.1 La remise en cause de la théorie de l’utilité espérée
1.1.1 La théorie de l’utilité espérée
Considérons un agent économique, un décideur, qui doit faire un choix dans une situation d’incertitude. L’agent sait qu’un seul état de la nature va se produire, mais il ne le connaît pas au moment de prendre sa décision. Suite à sa décision, le décideur fera face à des conséquences monétaires, qui dépendront de l’état de la nature qui va se réaliser. Lorsque le décideur a une connaissance objective des chances associées à chaque état de la nature, il fait face à une situation de risque, d’incertitude probabiliste. Dans cette situation, une représentation possible des décisions ayant un nombre fini de conséquences se fait en associant à chaque décision une distribution de probabilités (appelée loterie). Une loterie L = (x1p1;...; xnpn) correspond à une décision qui produit chaque conséquence xi avec une probabilité bien spécifiée pi. Un cas typique de ce type de situation est un jeu de roulette.
Dans un cadre plus général, le décideur ne dispose pas d’une connaissance objective des chances associées à chaque état de la nature et fait face à une situation d’incertitude non probabiliste. Afin de représenter la relation entre la réalisation de l’incertitude et les conséquences monétaires pour l’agent économique, on utilise habituellement ce qu’on appelle un « acte », qui correspond à une décision que peut prendre l’agent économique. Un acte peut être représenté comme une décision D = (x1E1;...; xnEn) qui conduit à la conséquence xi si l’évènement Ei se produit. Les évènements sont mutuellement exclusifs et ils décrivent de manière exhaustive l’ensemble des états de la nature, noté S[2]. L’acte résume ainsi les conséquences associées à la décision D. Cette situation correspond non plus à la roulette, mais à une situation analogue à une course de chevaux.
Dans le cadre de la théorie de l’utilité espérée subjective de Savage (1954), l’évaluation que le décideur fait d’une décision, ou acte, D est décrite par :
où u(.) est une fonction d’utilité et q(Ei) désigne la probabilité subjective associée à l’événement Ei. L’expression (1) nous montre que la théorie de l’utilité espérée subjective résulte de la combinaison de deux éléments : une règle d’utilité espérée, similaire à celle majoritairement employée dans les décisions risquées, et l’emploi d’une mesure de probabilité subjective. À une décision D = (x1E1;...;xnEn), cette mesure de probabilité subjective q fait correspondre une loterie (x1p1;...;xnpn), où chaque probabilité pi est telle que pi=q(Ei). Cette seconde propriété de la représentation des préférences du décideur est fondamentale. Elle correspond à la sophistication probabiliste (Machina et Schmeidler, 1992). En tant que telle, la sophistication probabiliste n’oblige pas l’évaluation de la décision à suivre une règle d’utilité espérée, elle impose seulement une règle de décision compatible avec l’emploi d’une distribution de probabilités. En ce sens, elle autorise des représentations bien plus générales que l’utilité espérée, compatibles par exemple avec le paradoxe d’Allais.
1.1.2 La théorie de l’utilité espérée face aux paradoxes d’Ellsberg
La sophistication probabiliste est cependant remise en cause par les paradoxes d’Ellsberg. Dans l’exemple à deux couleurs, la plupart des décideurs préfèrent prendre la décision D1. Si l’on représente l’incertitude par une distribution de probabilités, cela signifie que le décideur agit comme si la probabilité d’obtenir une boule rouge dans l’urne inconnue (évènement noté ER) était inférieure à 50 % (q(ER) < 1/2). Face au second choix proposé, un grand nombre de décideurs préfèrent prendre la décision D3. Si l’on représente l’incertitude par une distribution de probabilités, cela signifie que le décideur agit comme si la probabilité d’obtenir une boule noire dans l’urne inconnue (évènement noté EN) était inférieure à 50 % (q(EN) < 1/2). La comparaison directe avec le premier choix montre que ces deux décisions sont incompatibles avec la sophistication probabiliste qui implique que q(ER) + q(EN) = 1.
En fait, le décideur réagit au manque d’information sur le contenu de la seconde urne en lui préférant l’urne connue (Frisch et Baron, 1988). L’intérêt du paradoxe à deux couleurs est de montrer que le décideur a de l’aversion à l’ambiguïté, à l’incertitude sur la valeur de ses chances, et ce, indépendamment de toute violation (ou non-violation) de l’utilité espérée.
Dans le paradoxe à trois couleurs, la plupart des décideurs préfèrent prendre la décision D1, correspondant à l’option où la probabilité de gain est connue, plutôt que la décision D2. Dans la seconde situation de choix, c’est la décision D4, correspondant également à une situation de probabilité connue, qui est préférée. Notons ER, EN et EJ les évènements « la boule est rouge », « la boule est noire », « la boule est jaune ». Si l’on analyse les choix en termes de sophistication probabiliste, le choix de la décision D1 sur la décision D2 révèle que q(EN) < q(ER) = 1/3 alors que le choix de la décision D3 sur la décision D4 révèle que q(ER) + q(EJ) < q(EN) + (EJ) = 2/3. Dans un cas, les croyances révélées du décideur nous indiquent que q(EN) < q(ER) et dans l’autre cas, elles nous révèlent après simplification que q(EN) > q(ER). Ces choix sont donc une fois de plus incompatibles avec l’hypothèse de sophistication probabiliste. Si l’on souhaite néanmoins conserver cette hypothèse, en supposant que le renversement de préférence est lié à autre chose qu’à une violation de la sophistication probabiliste, on doit alors accepter des violations de dominance stochastique du premier ordre (Segal, 1987).
En termes d’axiomatique des préférences, les paradoxes d’Ellsberg remettent en cause l’axiome se trouvant au coeur de la théorie espérée : le principe de la chose sûre. Le principe de la chose sûre suggère que si deux décisions donnent les mêmes conséquences sur un ensemble d’évènements, alors remplacer ces conséquences communes par d’autres conséquences communes ne doit pas changer le choix du décideur. En d’autres termes, ces conséquences communes aux deux décisions sont sûres, quelle que soit la décision préférée et ne doivent donc pas influencer le choix. Le paradoxe à trois couleurs contredit ce principe : les décisions D1 et D2 ont une conséquence commune (0 $ si une boule jaune est tirée). Le deuxième choix ne diffère du premier qu’en remplaçant cette conséquence commune par 20 $. Le principe de la chose sûre prescrit alors de ne pas changer de choix, c’est-à-dire que préférer D1 devrait amener à préférer D3, et non D4 comme nombre d’individus le font.
1.2 Les modèles à croyances multiples
Le paradoxe d’Ellsberg a été confirmé par de nombreuses études (Camerer et Weber, 1992) et a suscité une large littérature théorique. Parmi les économistes, les modèles à croyances multiples ou modèles multiple priors, font partie des alternatives les plus populaires à l’utilité espérée. Dans cette famille de modèles, le plus connu est le modèle maxmin de Gilboa et Schmeidler (1989). L’article proposé par Jeleva et Tallon (2016), publié dans ce numéro, montre l’intérêt et la puissance de ce modèle pour rendre compte de l’impact de l’ambiguïté sur les marchés financiers.
1.2.1 Le modèle maxmin
Dans les modèles à croyances multiples, l’ambiguïté est prise en compte par un ensemble de croyances a priori, noté C ici[3]. L’ensemble C permet d’inclure les distributions de probabilité que le décideur pense possibles et d’exclure les autres. L’ensemble C peut également être vu comme la marge d’erreur qu’un décideur s’autorise autour d’une mesure de probabilité unique. L’évaluation d’une décision dans le modèle de Gilboa et Schmeidler (1989) se fait suivant un critère de type maxmin. La prise de décision consiste à évaluer toutes les utilités espérées induites par les différentes distributions de probabilités que le décideur considère comme possibles (incluses dans C), puis de retenir pour chaque décision, le minimum de ces utilités espérées. Le critère de décision représente donc les préférences non plus par Uq(D) comme dans l’expression (1) mais par le minimum d’un ensemble d’utilités espérées Uq(D) :
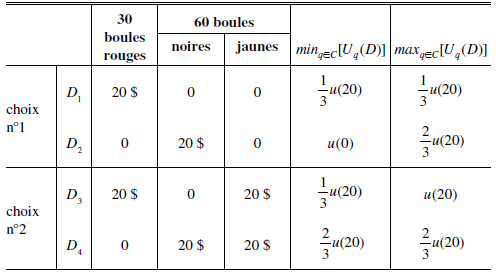
Le principe du maxmin consiste ainsi à choisir, pour chaque situation de choix, la décision offrant l’utilité espérée minimale la plus élevée. Ce modèle explique très simplement le comportement dans les exemples d’Ellsberg. Prenons l’exemple du paradoxe à trois couleurs avec un décideur qui considère uniquement les distributions physiquement possibles, c’est-à-dire telles que q(ER) = 1/3. Le tableau 2 donne les utilités espérées minimum associées à chaque décision. Le pessimisme du décideur le conduit à choisir la décision avec l’utilité espérée minimum la plus élevée dans chaque situation. La décision D1 est préférée à la décision D2 car elle ne comporte, au pire, qu’une chance sur trois d’obtenir 20 $, alors que la décision D2 ne comporte au pire, aucune boule gagnante. La décision D4 est préférée à la décision D3 car elle comporte au pire deux chances sur trois d’obtenir 20 $, alors que la décision D4 ne comporte au pire qu’une chance sur trois d’obtenir cette somme.
Tableau 2
Le paradoxe à trois couleurs et les modèles à croyances multiples : illustrations
Note : La colonne  donne le minimum d’utilité espérée lorsque l’ensemble C contient toutes les distributions de probabilités physiquement possibles (telles que q(ER) = 1/3). La colonne
donne le minimum d’utilité espérée lorsque l’ensemble C contient toutes les distributions de probabilités physiquement possibles (telles que q(ER) = 1/3). La colonne  donne le maximum d’utilité espérée dans ce cas.
donne le maximum d’utilité espérée dans ce cas.
Il est également possible d’illustrer le modèle maxmin dans le paradoxe à deux couleurs. Par exemple, un décideur qui considère qu’il y a entre 40 et 60 boules rouges dans l’urne inconnue prendra toujours l’hypothèse la plus pessimiste, quelle que soit la boule tirée. Son pessimisme le conduit à fonder ses décisions sur la pire situation dans le premier choix – 40 boules rouges gagnantes, procurant une utilité espérée minimum de 0.4u(20) – et dans le second choix – 40 boules noires gagnantes, procurant une utilité espérée minimum de 0.4u(20). Dans les deux cas, cette décision est dominée par la décision de retenir l’urne connue – 50 boules gagnantes, procurant une utilité espérée de 0.5u(20). Le modèle représente ainsi le niveau d’ambiguïté perçue par le décideur au moyen de l’ensemble C. Si l’ensemble C est grand (par exemple comprenant toutes les mesures de probabilités possibles), alors le décideur percevra beaucoup d’ambiguïté. Si l’ensemble C est restreint (par exemple, si le décideur considère que l’urne inconnue contient entre 49 et 52 boules rouges), alors le décideur percevra peu d’ambiguïté.
1.2.2 Le modèle α-maxmin
Le principe du maxmin, reposant sur un critère de Wald (1950), peut être critiqué pour son pessimisme extrême. Une fois admis ce principe, le seul moyen pour un décideur A d’avoir moins d’aversion pour l’ambiguïté qu’un décideur B est d’avoir un ensemble de croyances qui implique une perception plus faible de l’ambiguïté, par exemple en étant contenu dans celui de B. Ainsi, dans ce modèle, avoir moins d’aversion est équivalent à percevoir moins d’ambiguïté dans ce modèle. Le modèle dit α-maxmin de Ghirardato et al. (2004) tempère cet extrême pessimisme par de l’optimisme, représenté quant à lui de manière polaire par un critère de type maxmax. La combinaison de ces deux critères extrêmes permet de moduler l’attitude du décideur comme une moyenne pondérée du critère maxmin et du critère maxmax. Une décision est ainsi évaluée dans ce modèle comme une moyenne pondérée du minimum et du maximum d’utilité espérée atteignable, étant donné l’ensemble des croyances, le paramètre α contrôlant cette moyenne pondérée. Le critère de décision représente donc les préférences du décideur comme une moyenne :
Dans ce modèle, l’ensemble C représente comme précédemment le niveau d’ambiguïté perçu et le paramètre α représente l’attitude du décideur face à cette ambiguïté. Pour un niveau d’ambiguïté donné, plus α est important, plus le décideur pénalisera l’ambiguïté. À l’inverse, plus α est faible, plus l’ambiguïté sera désirable pour le décideur.
Le tableau 2 donne les utilités espérées minimum et maximum associées à chaque décision lorsque le décideur ne considère que les distributions de probabilité physiquement possibles. On remarque que pour une valeur α inférieure à ½, le décideur choisira la décision D2 plutôt que la décision D1 et la décision D3 plutôt que la décision D4, manifestant ainsi du goût pour l’ambiguité. Pour une valeur α supérieure à ½, on retrouve les choix habituels dans le paradoxe à deux couleurs[4].
En faisant varier le paramètre α, il est ainsi possible de prendre en compte tout un éventail d’attitudes vis-à-vis de l’ambiguïté, de l’aversion profonde (α proche de l’unité) au goût prononcé (α proche de zéro). Notons que α = ½ ne signifie pas forcément qu’il y a neutralité à l’ambiguïté (et utilité espérée à la Savage). Par exemple, considérons un décideur avec α = ½ ne disposant d’aucune information au sujet de trois évènements et leur assignant [0,1] dans son ensemble de croyances. Pour chaque évènement, ce décideur sera indifférent entre parier sur cet évènement et une chance objective de 50 %, agissant ainsi comme si les probabilités subjectives s’additionnaient à 150 %. Ainsi dans ce modèle, la séparation entre attitude vis-à-vis de l’ambiguïté et perception de l’ambiguïté est incomplète[5].
1.2.3 Les préférences variationnelles
La limite principale du modèle maxmin et du modèle α-maxmin réside dans leur profonde nature dichotomique : les mesures de probabilités sont soit considérées comme possibles et alors mises sur un pied d’égalité, soit considérées comme impossibles et dès lors totalement exclues de la prise de décision. Maccheroni et al. (2006) ont proposé un modèle dit de préférences variationnelles évitant cette dichotomie. Ce modèle fait varier de façon continue la manière dont les mesures de probabilité sont incluses dans le critère de choix. Cette extension est obtenue en introduisant un indice d’aversion à l’ambiguïté qui pénalise les utilités espérées associées aux distributions de probabilités qui n’ont pas la confiance du décideur. Le critère de décision est ici :
Plus c(q) est important, moins le décideur accorde de confiance aux utilités espérées associées à ces mesures de probabilité. On remarque que c(q) est défini sur ∆ et que s’il est nul pour les distributions de probabilités contenues dans un ensemble C et égal à l’infini sinon, alors le modèle se réduit au modèle maxmin, où l’ensemble C représente l’ensemble des croyances. L’intérêt du modèle de préférences variationnelles vient de sa grande flexibilité et de son grand degré de généralité. Ainsi, le modèle de préférences « à multiplicateur » à la Hansen et Sargent (2001, 2008), utile pour l’étude de la robustesse aux erreurs de spécification des modèles macroéconomiques, est un cas particulier de préférences variationnelles. Dans ce cadre, le décideur prend en compte la possibilité que son modèle macroéconomique ne soit pas le modèle qui décrive la réalité. L’indice d’aversion à l’ambiguïté s’écrit dans ce cas c(q) = θ.R(q || m), où R(q || m) mesure la vraisemblance relative des modèles alternatifs q par rapport au modèle de référence m du décideur (c’est-à-dire l’entropie relative par rapport à m) et θ ≥ 0 mesure le poids que le décideur accorde au fait que m ne soit pas le vrai modèle de la réalité. Lorsque θ augmente, le décideur pénalise davantage les modèles alternatifs et se focalise de plus en plus sur son modèle de référence. Le paramètre θ peut être rapproché d’un multiplicateur de Lagrange qui serait lié à une contrainte imposée sur l’entropie relative maximale que le décideur est prêt à considérer. D’où le nom de préférences « à multiplicateur ».
Dans le paradoxe d’Ellsberg à trois couleurs, il est probable que le décideur considère que le modèle de référence m est tel que m(ER) = m(EN) = m(EJ) = 1/3. Nous conservons l’hypothèse que le décideur ne considère que les distributions physiquement possibles, donc satisfaisant q(ER) = 1/3, et notons ici l’ensemble de ces distributions ∆p. Par conséquent, nous obtenons :
Le membre de gauche de l’inégalité est l’évaluation de D1 et celui de droite, l’évaluation de D2. Notons que l’entropie relative est positive et mesure la distance entre q et m. Sachant que m∈∆p et que ![]() , l’inégalité est toujours satisfaite pour m tel que m(ER) = m(EN) = m(EJ) = 1/3. En suivant des arguments similaires, nous obtenons l’inégalité suivante entre les évaluations de D3 et D4.
, l’inégalité est toujours satisfaite pour m tel que m(ER) = m(EN) = m(EJ) = 1/3. En suivant des arguments similaires, nous obtenons l’inégalité suivante entre les évaluations de D3 et D4.
Chateauneuf et Faro (2009) proposent un modèle « dual » au modèle de préférences variationnelles, où l’utilité espérée associée à chaque distribution de probabilités possible est corrigée en fonction du degré de confiance que l’individu lui attribue. Le décideur ne fonde sa décision que sur les distributions pour lesquelles il a une confiance minimale (supérieure à un seuil γ). Le critère de décision est ici :
L’intérêt de ce modèle réside dans sa représentation explicite du degré de confiance du décideur et dans le fait qu’il permette des applications aux choix financiers. Dans le paradoxe à trois couleurs, ce modèle explique les choix comme suit. Supposons (toujours) que le décideur ne considère que les distributions physiquement possibles et ait une fonction φ donnant une confiance maximale (égale à 1) à la distribution satisfaisant q(ER) = q(EN) = q(EJ) = 1/3. Par conséquent, D1 sera évaluée par 1/3u(20) car toutes les distributions considérées donnent cette utilité et la fonction min conduit à utiliser la distribution donnant une confiance maximale. De son côté, D2 donnera forcément une utilité au plus égale à celle de D1, car 1/3u(20) est certes possible mais la fonction min implique la recherche d’un niveau inférieur d’utilité. De même, D4 sera évaluée 2/3u(20) et D3 donnera forcément une utilité au plus égale à celle de D4.
1.2.4 Généralisations et prolongements
L’ensemble de ces modèles peut être unifié dans un modèle plus général de préférences avec aversion à l’incertitude (Cerreia-Vioglio et al., 2011). Ce modèle général montre le rôle central de l’axiome d’aversion à l’incertitude proposé initialement par Schmeidler (1989). Cet axiome implique qu’un décideur indifférent entre deux décisions préfèrera toujours combiner ces deux décisions plutôt que de prendre une seule des deux décisions. Cet axiome s’interprète aisément dans le cadre de l’exemple à 3 couleurs d’Ellsberg en ajoutant une cinquième décision D5 consistant à gagner 20 $ si la boule est jaune. Dans ce cas, le décideur sera indifférent entre parier sur une boule noire ou sur une boule jaune, c’est-à-dire entre les décisions D2 et D5. Mais si le décideur a de l’aversion pour l’incertitude, il préférera un mélange des deux décisions (0.5D2+0.5D5) à chacune des décisions isolées. Cela revient à construire un acte qui donne dans chaque état possible (EN , EJ) une loterie associant la probabilité ½ à chaque conséquence possible des deux actes initiaux D2 et D5. La raison de cette préférence repose sur la volonté de se protéger de l’incertitude par la construction d’une loterie (20,½; 0,½). Notons que cet axiome est également central pour relier le modèle maxmin aux modèles dépendant du rang et pour généraliser le modèle maxmin à la décision en présence de risque (Dean et Ortoleva, 2012).
Gajdos et al. (2008) utilisent le modèle maxmin en définissant l’ensemble des croyances C comme l’ensemble des distributions de probabilités compatibles avec l’information dont dispose le décideur. Dans ce modèle, la règle de décision est la combinaison d’une règle maxmim et de l’espérance d’utilité évaluée sur une distribution de probabilités de référence, constituant une sorte de valeur moyenne de l’ensemble des croyances. De ce fait, le modèle a comme sous-cas l’utilité espérée, quel que soit l’ensemble des croyances, contrairement au modèle α-maxmin. L’intérêt de ce modèle repose sur la possibilité de comparer des décisions lorsque les structures d’information objectives disponibles sont très dissemblables. Dans ce modèle, lorsque le décideur a de l’aversion à l’égard de l’imprécision, il va accorder plus de poids au critère bayésien fondé sur la distribution de référence qu’au critère pessimiste de décision maxmin fondé sur l’imprécision inhérente à l’ensemble C.
1.3 Les modèles à plusieurs étapes
1.3.1 Les distributions de second ordre
Si l’on considère que l’ensemble de croyances reflète uniquement l’information objective disponible sur l’état du monde, le contenu comportemental de l’ensemble C de croyances est relativement faible. Les éléments de l’ensemble de croyances se résument alors à autant de scénarios possibles, énumérés un à un, et construire l’ensemble des croyances revient alors à recenser tous les scénarios possibles comme autant de processus générateurs de données, de distributions de probabilité q. Afin de prendre en compte les comportements, il est nécessaire de compléter ces scénarios possibles par des croyances sur la vraisemblance de chaque scénario. Ainsi, les distributions de premier ordre, qui sont des scénarios factuels, doivent être complétées par une distribution des croyances portant sur chaque scénario décrit par l’ensemble des croyances. Cette nouvelle distribution, au contenu comportemental, est en général dénommée distribution de second ordre (Marschak, 1975). Dans ce type de représentation, la décision est la combinaison de deux étapes : une étape terminale objective (les distributions de premier ordre) où se trouvent différent scénarios[6] et une étape initiale contenant des distributions de probabilités sur ces scénarios (distribution de second ordre).
Dans un cadre purement bayésien, cette structure se ramène à une unique distribution de probabilités, du fait de la réduction des loteries composées qui permet de réduire le choix à une situation à une seule étape. Cependant, dès lors que la réduction n’est plus satisfaite, des attitudes vis-à-vis de l’ambiguïté, autres que la neutralité, peuvent émerger.
1.3.2 L’aversion à l’ambiguïté et la violation de la réduction des loteries composées
Segal (1987) est un des premiers à avoir utilisé ce type de modèle à deux étapes pour expliquer le comportement individuel dans le paradoxe d’Ellsberg. Il montre que si le décideur ne satisfait pas la réduction des loteries composées et se comporte suivant un modèle dépendant du rang en présence de risque[7], il est possible d’expliquer l’aversion à l’ambiguïté sans même avoir recours à aucun modèle d’ambiguïté. En effet, dans ce cas, le décideur préfère connaître la probabilité de l’unique scénario associé à l’urne connue plutôt que de connaître l’ensemble de scénarios de l’urne inconnue, bien qu’en espérance les probabilités soient les mêmes dans les deux urnes. C’est l’aversion du décideur aux loteries à plusieurs étapes qui fait qu’il a de l’aversion pour l’urne inconnue. Ainsi selon Segal (1987), un simple modèle de décision non bayésien en présence de risque suffit à expliquer le phénomène d’aversion à l’ambiguïté : cette dernière est prise en compte par l’attitude vis-à-vis des distributions de second ordre et tout modèle spécifique de décision en ambiguïté devient inutile.
1.3.3 Le modèle lisse d’aversion à l’ambiguïté
Le modèle de Klibanoff et al. (2005) repose également sur le fait que le décideur possède une distribution de second ordre sur ses chances. Cette distribution de second ordre représente les croyances subjectives du décideur. Les croyances de second ordre reflètent la vision que le décideur se fait de l’ambiguïté ou de l’information disponible. Dans ce qui suit, leur distribution est notée µ et la probabilité qu’un scénario q soit la vraie distribution de probabilités est notée µ(q). Dans le modèle de Klibanoff et al. (2005), les préférences sont représentées par une double espérance : une première espérance d’utilité pour chaque scénario possible, une seconde espérance fondée sur la distribution de second ordre transformant à son tour les espérances d’utilité des différents scénarios. L’évaluation d’un acte se fait ainsi selon :
Les espérances d’utilité Uq associées aux distributions de premier ordre sont ici transformées, distordues de manière non-linéaire par une fonction ϕ(.). L’espérance de ces espérances d’utilité transformées est alors évaluée avec la distribution de probabilités µ, représentant l’ambiguïté perçue. L’élément essentiel du modèle est la fonction de transformation ϕ(.). Cette fonction représente l’attitude du décideur à l’égard de l’ambiguïté. Si la fonction ϕ(.) est concave, le décideur met plus de poids sur les faibles utilités espérées, donc sur les mauvais scénarios. Ce pessimisme traduit directement de l’aversion à l’égard de l’ambiguïté. À l’inverse, si la fonction ϕ(.) est convexe, le décideur accorde plus d’importance aux niveaux élevés d’utilité espérée, donc aux bons scénarios, et il présente alors du goût pour l’ambiguïté.
Afin d’illustrer ce modèle, nous reprenons le paradoxe à trois couleurs pour montrer le lien entre aversion à l’ambiguïté et forme de la fonction ϕ(.). Comme précédemment, le décideur ne prend en compte que les distributions physiquement possibles (telles que q(ER) = 1/3) et donc toute distribution q ne satisfaisant pas cette condition se verra assigner une probabilité µ(q)=0. Toutes les autres distributions q satisfont q(EJ) = 2/3 − q(EN) et peuvent donc être identifiées de manière unique par q(EN)∈[0, 2/3]. Nous supposons en outre que µ est uniforme sur [0, 2/3]. L’espérance de q s’écrit donc ![]() . Par conséquent, si ϕ est concave, par l’inégalité de Jensen, on obtient[8] :
. Par conséquent, si ϕ est concave, par l’inégalité de Jensen, on obtient[8] :
Le premier membre de l’inégalité correspondant à l’évaluation de D2 et le second à celle de D1, on retrouve donc la préférence pour D1. Par le même raisonnement et si ϕ est concave :
ce qui prédit une préférence pour D4 (le membre de droite) par rapport à D3 (le membre de gauche), comme dans les exemples d’Ellsberg.
La force du modèle de Klibanoff et al. (2005) est triple. Elle repose tout d’abord sur cette analogie directe entre la fonction ϕ(.) et la fonction d’utilité u(.). La fonction de transformation représente l’aversion à l’ambiguïté comme la fonction d’utilité représente l’aversion au risque, par son degré de concavité. La force du modèle repose également sur l’analogie avec les modèles récursifs d’utilité espérée. Une fonction ϕ(.) concave correspond à une aversion aux accroissements de variance à moyenne inchangée en termes d’utilité espérée, et donc à une préférence pour la seconde étape sur la première étape. Enfin la force du modèle vient de sa différentiabilité, qui autorise des applications apparemment bien plus directes aux modèles économiques traditionnels que les autres modèles d’ambiguïté (Gollier, 2011, pour une application aux choix d’actifs). Des modèles à plusieurs étapes ont également été proposés par Nau (2006), Ergin et Gul (2009) ou Seo (2009). Nous renvoyons le lecteur intéressé à leur exposition dans Machina et Sinischalchi (2014).
1.4 Les modèles dépendant du rang
La troisième grande classe de modèles d’ambiguïté est constituée des modèles dépendant du rang. Le modèle dépendant du rang en présence d’ambiguïté est parfois appelé utilité à la Choquet–CEU pour Choquet expected utility (Schmeidler, 1989, Wakker, 1990). Lorsqu’il intègre un traitement différent des gains et des pertes, on peut alors parler de prospect theory en présence d’ambiguïté (Wakker, 2010)[9].
1.4.1 L’utilité à la Choquet
Comme dans tout modèle dépendant du rang, il est nécessaire de spécifier le rang des conséquences. Nous supposons donc que les conséquences associées à une décision sont classées par ordre décroissant de préférence (x1 ![]() x2
x2 ![]() …
… ![]() xn ). Dans le modèle dépendant du rang, les probabilités subjectives sont remplacées par des poids de décision πi associés à la valeur subjective de chaque conséquence xi.
xn ). Dans le modèle dépendant du rang, les probabilités subjectives sont remplacées par des poids de décision πi associés à la valeur subjective de chaque conséquence xi.
Afin de définir les poids de décision, l’élément central est la notion de rang. Le rang Ri d’une conséquence xi se définit comme l’évènement qui produit des conséquences strictement meilleures que xi : ![]() . Pour la conséquence de rang 1, le rang est l’ensemble vide R1 = ∅.
. Pour la conséquence de rang 1, le rang est l’ensemble vide R1 = ∅.
Dans le cadre de l’utilité à la Choquet, les poids de décision associés à une conséquence xi sont générés par une mesure qui n’est pas nécessairement additive W[10]. La notion de capacité permet de prendre en compte le fait que l’attention portée à un évènement dépend non seulement des conséquences de cet évènement mais également de la position relative de ces conséquences par rapport à celles induites par les autres évènements (Diecidue et Wakker, 2001). Le poids de décision associé à une conséquence xi se définit alors comme la variation dans la fonction de pondération du rang, due à l’évènement associé à cette conséquence :
Si la capacité W est une mesure additive, alors le poids de décision associé à la conséquence xi est πi = W(Ei). Chaque poids de décision ne dépend alors que de Ei et correspond à la probabilité subjective associée aux évènements q et l’utilité à la Choquet correspond à l’utilité espérée de Savage (1954).
L’utilité espérée à la Choquet explique les choix dans le paradoxe d’Ellsberg à trois couleurs de manière simple. Le choix de la décision D1 sur la décision D2 révèle que W(ER) > W(EB), alors que le choix de la décision D4 sur la décision D3 révèle que ![]() . Si les capacités sont telles que
. Si les capacités sont telles que ![]() = 1 / 3, W(EB) = 0 et
= 1 / 3, W(EB) = 0 et ![]() par exemple, il est possible de rationaliser les choix effectués par le décideur.
par exemple, il est possible de rationaliser les choix effectués par le décideur.
1.4.2 L’intégration avec les modèles dépendant du rang en présence de risque
Un lien utile peut être établi entre les représentations en présence de risque et d’ambiguïté en supposant que la sophistication probabiliste est vérifiée. Dans ce cas, la capacité correspond à la composition d’une transformation de probabilité w et d’une probabilité subjective[11]. Le poids de décision se définit alors de la manière suivante :
Cette formulation permet d’envisager la pondération des évènements comme le résultat d’un processus où les probabilités subjectives sont d’abord formées, puis transformées comme si elles étaient des probabilités objectives, pour former les poids de décision. Cette représentation correspond à la distinction opérée par Keynes (1921) entre la mesure et le poids de l’évidence empirique. Les probabilités subjectives ont pour rôle de mesurer l’évidence empirique. Cependant le poids accordé à cette mesure peut différer selon la quantité d’information sur laquelle est fondée cette mesure. La formulation présentée par l’équation (6), bien que séduisante, a cependant deux inconvénients. D’une part, elle nécessite une mesure de probabilité q qui classe les évènements de la même manière que W (Chateauneuf, 1985). D’autre part, cette formulation ne permet pas d’expliquer le paradoxe d’Ellsberg, car elle suppose la sophistication probabiliste. Cette représentation peut toutefois être adaptée pour inclure les comportements face à l’ambiguïté et la fonction w est utile, notamment face à différentes sources d’incertitude, pour identifier l’influence de la source d’incertitude sur l’attitude du décideur (Abdellaoui et al., 2011). Dans ce cadre, le décideur forme une probabilité subjective pour chaque source d’incertitude dans une première étape puis le transforme à l’aide d’une fonction de transformation dépendante de chaque source d’incertitude dans une seconde étape.
Si la complexité du modèle peut constituer un frein à son application dans les modèles économiques, la capacité de mesurer simplement l’attitude du décideur face au risque et à l’ambiguïté constitue un des principaux attraits des modèles dépendant du rang. Contrairement aux deux autres grandes catégories de modèles qui reposent sur des éléments difficilement quantifiables sans hypothèses supplémentaires (ensemble de croyances, distributions de second ordre...), les modèles dépendant du rang permettent de mesurer des poids de décision à l’aide de choix simples et de variations exogènes de l’environnement de choix[12]. Par ailleurs, ces modèles résolvent à la fois les paradoxes d’Allais et d’Ellsberg dans un cadre d’analyse unifié.
1.5 Autres modèles
Au-delà des trois grandes classes de modèles présentés ci-dessus, de nombreux autres modèles ont été développés pour prendre en compte l’attitude à l’égard de l’ambiguïté. La vaste littérature existant sur ce sujet rend illusoire toute volonté d’exhaustivité. Pour mémoire, la revue de littérature de Machina et Siniscalchi (2014) recense pas moins de 12 types de modèles différents. Dans cet article, à titre illustratif, nous présentons rapidement deux modèles d’ambiguïté qui nous semblent particulièrement attrayants : le modèle vectoriel et les préférences unanimes.
1.5.1 Le modèle vectoriel
Le modèle vectoriel de Siniscalchi (2009) suppose que le décideur ancre son évaluation de l’incertitude sur une évaluation de type utilité espérée, correspondant à l’équation (1), à partir d’une distribution de probabilités de base. Puis, son évaluation fait l’objet d’un ajustement reflétant la perception que le décideur a de l’ambiguïté ainsi que son attitude face à l’ambiguïté. L’ajustement réalisé par le décideur se fait en fonction de l’exposition à l’ambiguïté et de la variabilité de l’ambiguïté. Le critère de décision se fonde donc sur un critère d’utilité espéré associé à la distribution de base auquel s’ajoute un ajustement, fonction de la covariance entre cette utilité et l’exposition à l’ambiguïté dans chaque source d’incertitude. L’intérêt du modèle de Siniscalchi (2009) est double. D’une part, le modèle repose sur une analogie avec les modèles de prix des actifs : l’évaluation est fonction d’un terme de référence (une espérance d’utilité) auquel s’ajoute un terme de covariance (d’utilité)[13]. D’autre part, le modèle prend en compte explicitement la notion d’exposition à l’ambiguïté. Par exemple, dans le paradoxe à trois couleurs, l’exposition à l’ambiguïté des décisions D1 ou D4 est nulle, mais elle n’a pas pour autant la même origine. Dans le cas de D1, l’exposition à l’ambiguïté est nulle par définition et il n’y a pas de variabilité possible de l’utilité espérée. Dans le cas de D4, l’exposition à l’ambiguïté est nulle car les variabilités possibles dans l’utilité espérée s’annulent l’une l’autre. Autrement dit, la complémentarité entre les deux sources d’ambiguïté EN et Ej se traduit par une covariance nulle, qui attire le décideur.
1.5.2 Les préférences unanimes
Les préférences unanimes sont un cas très particulier d’étude des préférences en présence d’incertitude proposé par Bewley (2002). Dans ce modèle, et contrairement aux modèles précédents, certaines décisions ne sont tout simplement pas comparables. Cette représentation des préférences incomplètes en présence d’incertitude se fonde sur un ensemble de croyances C. Dans ce modèle, pour qu’une décision soit prise, il est nécessaire qu’elle le soit non pas parce qu’elle assure le niveau minimal d’utilité espérée, comme dans le modèle maxmin, mais parce que toutes les croyances possibles dans l’ensemble C s’accordent sur le fait que cette décision est la meilleure (règle d’unanimité). Du fait de la règle d’unanimité, il est dans de nombreux cas impossible de prédire la décision. Par exemple dans le paradoxe à trois couleurs, si le décideur considère les distributions physiquement possibles, il ne peut pas classer D1 et D2. Sur une partie de l’ensemble des croyances (celles pour lesquelles q(EN) > 1/3), la décision serait en faveur de D1, mais sur l’autre partie de l’ensemble des croyances (celles pour lesquelles q(EN) < 1/3), la décision serait en faveur de D2. Il n’y a donc pas unanimité possible sur cet ensemble de croyances[14] et le décideur ne peut prendre une décision. Il peut être alors nécessaire de compléter le modèle par des hypothèses additionnelles spécifiant le comportement du décideur lorsque la règle d’unanimité l’empêche de prendre une décision. Une telle hypothèse spécifie par exemple que le décideur a tendance à choisir l’inertie tant que ses croyances ne sont pas unanimes sur la possibilité de se tourner vers une décision plus avantageuse.
2. Évaluation empirique des modèles de décision en présence d’incertitude
2.1 Mesures et évidence de l’aversion à l’ambiguïté
2.1.1 L’expérience de Becker et Brownson (1964)
Fellner (1961) et Becker et Brownson (1964) font partie des premiers à présenter des résultats concernant l’aversion à l’ambiguïté dans le cadre proposé par Ellsberg. Obtenus auprès d’étudiants, leurs résultats confirment l’existence d’une aversion à l’ambiguïté mesurée sur de simples choix binaires dans le paradoxe à deux couleurs[15].
Dans l’expérience de Becker et Brownson (1964), les participants étaient d’abord confrontés au paradoxe à deux couleurs original, puis à 10 choix entre des urnes présentant un degré d’ambiguïté variable (c’est-à-dire contenant un nombre de boules rouges compris entre 0 et 100, 40 et 60, 25 et 75, 15 et 85 et, bien sûr égal à 50). Les participants devaient également donner leur propension à payer pour obtenir leur urne préférée pour chacun des 10 choix. Les résultats montrent que 44 % des sujets[16] avaient de l’aversion à l’égard de l’ambiguïté et que ces derniers étaient prêts à payer une prime de l’ordre de 70 % de l’espérance de la loterie pour éviter l’urne totalement ambiguë. Les résultats suggèrent également que la prime d’ambiguïté décline lorsque le degré d’ambiguïté diminue (jusqu’à 30 % environ pour éviter l’urne avec un nombre de boules rouges comprises entre 40 et 60). MacCrimmon et Larsson (1979), Curley et Yates (1985) ou Kahn et Sarin (1988) ont confirmé ces résultats. Dans les situations de pertes, le phénomène semble s’inverser. Les individus y ont moins d’aversion à l’égard de l’ambiguïté lorsque le degré d’ambiguïté augmente (Curley et Yates, 1985; Hogarth et Einhorn, 1990).
2.1.2 Variations expérimentales sur les paradoxes d’Ellsberg
La littérature expérimentale a également montré que les individus avaient de l’aversion à l’égard de l’ambiguïté dans le paradoxe d’Ellsberg à trois couleurs, et ce, dans des proportions encore plus importantes que celles observées dans le cas du paradoxe à deux couleurs. Ainsi, Slovic et Tversky (1974) ou Curley et al. (1986) obtiennent des proportions de choix avec aversion à l’ambiguïté de l’ordre de 80 %. Ces proportions demeurent les mêmes lorsque les principes gouvernant la théorie de l’utilité espérée sont préalablement clairement indiqués aux participants. L’aversion à l’ambiguïté demeure également quand le degré d’ambiguïté diminue, par exemple quand des tirages successifs sont effectués au sein de l’urne inconnue (Gigliotti et Sopher, 1992). Il convient de noter que MacCrimmon et Larsson (1979), en faisant varier le nombre de boules rouges dans l’urne, montrent que l’aversion à l’ambiguïté est particulièrement forte lorsque la proportion est égale à 1/3, ce qui correspond exactement à l’exemple d’Ellsberg.
En comparant des équivalents certains déterminés sur des urnes connues et des urnes inconnues, Cohen et al. (1987) montrent que les participants ont nettement plus d’aversion à l’égard de l’ambiguïté dans les gains (59 % des participants) que dans les pertes (25 % des participants). Il apparaît également dans cette étude que l’aversion à l’ambiguïté est peu corrélée à l’aversion au risque au niveau individuel, un résultat confirmé depuis par de nombreuses études expérimentales. Tentant de mettre en relation le comportement des participants dans le paradoxe à deux couleurs et le fait qu’ils se conforment ou non à la réduction des loteries composées, Halevy (2007) montre que les individus qui satisfont cet axiome sont en général neutres vis-à-vis de l’ambiguïté.
2.1.3 La question de la validité interne
Les résultats obtenus dans le paradoxe à deux couleurs sont cependant soumis à des questions portant sur la validité interne des expériences répliquant l’exemple d’Ellsberg. En effet, il est possible que le protocole même de l’expérience d’Ellsberg génère le phénomène d’aversion à l’ambiguïté. Fox et Tversky (1995) posent explicitement cette question, à savoir : l’aversion à l’ambiguïté est-elle un phénomène spécifique aux paradoxes d’Ellsberg ou s’agit-il d’un phénomène plus général? Afin de répondre à cette question, Fox et Tversky (1995) construisent une série d’expériences fondées sur les exemples d’Ellsberg et au fil desquelles l’information concernant les urnes est présentée de manière différente (tantôt séparée, tantôt conjointe). Lorsque les individus doivent évaluer les urnes connue et inconnue de manière isolée, il n’y a pas de différence significative entre les évaluations faites dans les deux cas par les différents participants. Au contraire, en présence des deux urnes, l’évaluation de l’urne connue augmente significativement, signalant sa forte attractivité. Ainsi, le phénomène d’aversion à l’ambiguïté dans le paradoxe d’Ellsberg serait principalement lié au contraste informationnel entre les deux urnes, qui ferait ressortir l’absence d’information du décideur quant au contenu de l’urne inconnue et le pousserait à surévaluer l’information disponible dans l’urne connue. Fox et Tversky (1995) montrent que le même phénomène se produit dans le paradoxe à trois couleurs : l’évaluation de la décision D4 dépend fortement de la possibilité de la comparer avec la décision D3. Chow et Sarin (2001) montrent cependant que, si l’aversion à l’ambiguïté est réduite dans les situations non comparatives, elle demeure néanmoins présente, notamment au niveau individuel. Si l’aversion à l’ambiguïté est sensible au contraste avec les situations d’incertitude, elle semble donc persister comme phénomène autonome.
2.1.4 Paradoxes d’Ellsberg et sources d’incertitude
Abdellaoui et al. (2011) analysent le choix dans le paradoxe d’Ellsberg à deux couleurs comme un choix entre deux sources d’incertitude et proposent une méthode de mesure des attitudes vis-à-vis de l’ambiguïté dans ce cadre. Cette méthode repose en particulier sur l’utilisation de fonctions « sources » qui transforment les probabilités, objectives ou subjectives, en poids de décision. Chaque type d’ambiguïté, appelée source d’incertitude, est caractérisé par une fonction source propre. Les fonctions sources saisissent les attitudes vis-à-vis de l’incertitude et peuvent être résumées par deux indices. Le premier indice résume le degré de pessimisme d’un agent. Cet indice traduit la tendance globale à sous-pondérer toute probabilité d’un évènement favorable. Un pessimisme plus important face à l’incertitude que face au risque traduira de l’aversion à l’ambiguïté. Cet élément peut être vu comme un facteur d’attractivité : l’incertitude attire moins que le risque. Le second indice représente le degré d’insensibilité aux variations de vraisemblance[17]. Cet élément peut être vu comme un facteur cognitif : il peut être plus difficile de réaliser des évaluations en maniant des probabilités subjectives qu’en maniant des probabilités objectives. Les résultats expérimentaux obtenus dans ce cadre montrent que les individus sont plus insensibles aux variations de vraisemblance en présence d’incertitude (l’urne inconnue) qu’en présence de risque (l’urne connue). Les résultats montrent également un optimisme plus grand pour les sources proches ou familières d’incertitude (par exemple la température locale) que pour les sources plus lointaines (par exemple la température dans un pays étranger).
2.2 Les tests des modèles d’ambiguïté
Au cours des dernières années, un certain nombre de travaux ont tenté de déterminer quel modèle d’ambiguïté était le meilleur pour représenter les comportements individuels, sans pour autant qu’un consensus clair ne se dégage.
2.2.1 La diversité des évaluations des modèles d’ambiguïté
L’expérience d’Halevy (2007) suggère que deux tiers des participants ont un comportement compatible avec un modèle à deux étapes (dont un tiers avec le modèle dépendant du rang de Segal. 1987 et un tiers avec un modèle de type Klibanoff et al., 2005). Seuls 19 % des participants ont un comportement compatible avec le modèle d’utilité espérée. Conte et Hey (2013) utilisent des choix entre des loteries à deux étapes et aboutissent à des résultats similaires. Dans cette expérience, les loteries de la seconde étape (les scénarios possibles) sont progressivement éliminées dans les choix proposés aux sujets. Les résultats suggèrent qu’environ la moitié des participants se conforment au modèle de Klibanoff et al. (2005), un quart au modèle d’utilité espérée et environ 20 % au modèle dépendant du rang. Cubitt et al. (2012) déterminent les équivalents certains correspondant à des loteries à deux étapes afin d’estimer les paramètres du modèle de Klibanoff et al. (2005) et d’éliciter les primes d’ambiguïté correspondantes au niveau individuel. Les primes d’ambiguïté sont égales à 7 % de la valeur espérée et sont comparables aux primes de risque (de l’ordre de 11 %).
Epstein (2010) a proposé un ensemble de choix simples pouvant mettre en difficulté le modèle de Klibanoff et al. (2005). Cubitt et al. (2012) ont implanté dans un cadre expérimental les choix proposés par Epstein. Pour les sujets ayant de l’aversion à l’ambiguïté, les résultats vont dans le sens du modèle de Klibanoff et al. (2005), mais pour la majorité des participants, l’expérience ne permet pas de discriminer entre les modèles d’ambiguïté et le modèle d’utilité espérée. Ahn et al. (2014) obtiennent des résultats similaires en utilisant des choix de portefeuille expérimentaux. On utilise les choix pour estimer deux grandes catégories de modèles : d’une part, les modèles qui conduisent à des courbes d’indifférences « lisses » (ce qui correspond à la théorie de l’utilité espérée ou au modèle de Klibanof et al., 2005) et ceux qui présentent des courbes d’indifférence avec un coin. Cette dernière catégorie recouvre les modèles de type maxmin et d’utilité dépendante du rang (pour une description, voir Cohen et Tallon, 2000). Les résultats d’Ahn et al. (2014) montrent que pour environ 60 % des sujets, le comportement reste compatible avec la théorie de l’utilité espérée. Les modèles d’ambiguïté ne sont donc apparemment que d’un intérêt limité pour une majorité d’individus. Cependant dans cette expérience, il est difficile de séparer clairement les individus qui suivent un modèle d’utilité de ceux qui ont un comportement compatible avec un modèle de type Klibanoff et al. (2005). Pour les 40 % d’individus restants, il apparaît que les modèles de type Klibanoff et al. (2005) ne sont pas les plus appropriés pour représenter l’attitude à l’égard de l’ambiguïté.
Hey et al. (2010) s’intéressent au pouvoir prédictif des modèles d’ambiguïté à partir d’un ensemble de choix binaires entre des actes à trois conséquences. Les modèles considérés sont entre autres les modèles à croyances multiples et les modèles dépendant du rang. Les modèles à plusieurs étapes ne sont pas considérés. Les résultats suggèrent que les modèles d’ambiguïté sont globalement peu satisfaisants pour rendre compte des comportements et que des représentations du choix fondées sur des heuristiques obtiennent de meilleures performances descriptives. Cependant, reprenant les données de Hey et al. (2010) et en les analysant à l’aide de la méthode proposée par Abdellaoui et al. (2011), Kothiyal et al. (2014) obtiennent des conditions plus favorables aux modèles dépendant du rang et à ceux à croyances multiples. Hayashi et Wada (2010) montrent les difficultés empiriques du modèle à croyances multiples et du modèle α-maxmin en montrant que les individus ne se focalisent pas uniquement sur les croyances produisant les utilités maximales et minimales, mais prennent également en compte les croyances générant des niveaux intermédiaires d’utilité. Yang et Yao (2014) proposent une expérience dans laquelle le décideur tire plusieurs fois avec remise dans des urnes à la Ellsberg, générant des accroissements de variance à moyenne constante. Les résultats sont compatibles avec un modèle dépendant du rang mais non avec un modèle à croyances multiples ou avec le modèle de Klibanoff et al. (2005). Des résultats similaires sont également obtenus par Chew et al. (2013), qui montrent que leurs données expérimentales ne sont pas compatibles avec le modèle de Siniscalchi (2009).
Tableau 3
Les tests des modèles d’ambiguïté
Note : KMM correspond à Klibanoff et al. (2005), SEU correspond à la théorie de l’utilité espérée, CEU correspond à l’utilité à la Choquet, VEU correspond au modèle de Siniscalchi (2009).
Machina (2009) a soulevé la possibilité que l’utilité à la Choquet et les modèles à dépendance de rang soient invalidés par des exemples construits dans un esprit similaire à celui d’Ellsberg[18]. Le principe de la remise en cause de la dépendance du rang proposée par Machina (2009) apparaît dans son exemple dit de la « réflexion ». Cet exemple modifie le paradoxe d’Ellsberg à trois couleurs en l’étendant aux situations où il y a au moins trois conséquences. L’Haridon et Placido (2010) confirment la validité empirique du paradoxe d’Ellsberg ainsi modifié. Baillon et al. (2011) montrent que ces exemples conduisent non seulement à la violation des modèles dépendant du rang, mais également à celle des modèles à croyances multiples et des modèles à plusieurs étapes. Ces résultats montrent qu’aucun des modèles phares ne permet de rendre compte des comportements dans l’exemple de la réflexion. Des modèles plus généraux, comme le modèle de Siniscalchi (2009) qui intègre la perception de l’ambiguïté par la prise en compte de complémentarités entre évènements, permettent cependant de le faire.
2.2.2 La question de l’hétérogénéité des méthodes et des résultats
L’ensemble des études que nous venons de présenter montrent une grande hétérogénéité au sein de la littérature, à la fois dans les méthodes mais également dans les résultats obtenus concernant les modèles d’ambiguïté. Concernant les méthodes expérimentales, ces études utilisent toutes des manipulations expérimentales plus ou moins sophistiquées pour représenter des urnes inconnues à la Ellsberg. Selon la spécification du protocole expérimental, l’accent est mis sur tel ou tel modèle d’ambiguïté, ne permettant pas de réelle vision d’ensemble de la performance relative de chacun des modèles. Concernant les résultats, ces études obtiennent des résultats diamétralement opposés concernant le pouvoir explicatif de la théorie de l’utilité espérée, des modèles dépendant du rang ou du modèle de Klibanoff et al. (2005). Cette diversité peut sembler insatisfaisante. Baillon et Bleichrodt (2015) présentent un cadre expérimental se démarquant explicitement du cadre habituel (consistant à utiliser des urnes à la Ellsberg) en utilisant l’incertitude liée à un évènement réel (l’évolution d’un indice de marché). Par ailleurs, les auteurs se focalisent avant tout sur le fondement des paradoxes d’Ellsberg, à savoir la sophistication probabiliste, afin d’évaluer les différents modèles en regard de cet élément fondamental. Cette stratégie permet en outre de mobiliser un protocole expérimental simple reposant sur l’élicitation de probabilités équivalentes[19]. Baillon et Bleichrodt (2015) montrent en quoi le type de violation de la sophistication probabiliste révélé par ces choix permet d’inférer de l’information sur la validité descriptive des modèles d’ambiguïté. Les résultats indiquent que la sophistication probabiliste est clairement violée, tant dans les gains que dans les pertes, mais selon des modalités différentes. Une structure en quatre parties, similaire à celle observée par Kahneman et Tversky (1979) en présence de risque, apparaît : goût pour l’ambiguïté face à des gains peu vraisemblables et à des pertes vraisemblables, aversion à l’ambiguïté face à des gains vraisemblables et à des pertes peu vraisemblables.
Du fait de la dépendance au signe, la prospect theory apparaît ici bien placée pour expliquer les résultats obtenus. De manière générale, les modèles qui autorisent une large variété d’attitudes vis-à-vis de l’ambiguïté sont mieux pour expliquer les comportements observés en laboratoire, ce qui est le cas pour les modèles dépendant du rang et le modèle α-maxmin. À l’inverse, les données sont difficilement compatibles avec les modèles qui prédisent l’uniformité des attitudes vis-à-vis de l’ambiguïté, à savoir les modèles maxmin et de préférences variationelles, le modèle de Klibanoff et al. (2005) avec fonction de transformation concave ou convexe et le modèle de Siniscalchi (2009). Dans le même ordre d’idées, Abdellaoui et al. (2014) mesurent les croyances individuelles concernant deux sources naturelles d’incertitude, une température future locale et étrangère, et concluent que les modèles d’utilité récursive présentent de moins bonnes performances descriptives que les modèles concurrents, modèles dépendant du rang ou modèles à croyances multiples.
Conclusion
Dans cet article, nous avons présenté les principaux modèles d’ambiguïté qui ont été proposés dans le but de pallier les difficultés descriptives de la théorie de l’utilité espérée. La plupart de ces modèles ont été construits en réaction aux paradoxes d’Ellsberg. Comme nous l’avons vu, les tentatives pour modifier la théorie de l’utilité espérée sont allées dans de multiples directions et font encore l’objet de débats. En ce sens, les modèles d’ambiguïté ne présentent pas l’aspect de théorie unifiée qui fait toujours la force de la théorie de l’utilité espérée. Au mieux, ils permettent de disposer d’une palette de représentations permettant d’amender le modèle standard par la prise en compte d’une confiance limitée du décideur dans ses croyances. Les débats sur l’intérêt respectif de ces modèles portent non seulement sur l’intérêt de telle ou telle représentation des préférences mais également sur les fondements de ces préférences. En particulier, la place centrale de l’axiome d’aversion à l’égard de l’incertitude dans de nombreuses axiomatiques de la décision en présence d’ambiguïté reste sujette à débat, de même que les hypothèses sous-jacentes au modèle « lisse » d’ambiguïté. Au niveau empirique, nous avons vu que les tests des modèles d’ambiguïté ne permettent pas, dans l’état actuel de la littérature, de disposer d’une vision claire du modèle qui serait pertinent pour rendre compte des comportements observés en laboratoire et a fortiori des comportements observés dans la réalité. Il serait crucial de savoir si certains modèles sont plus adaptés à certaines situations (finance, organisations, jeux, comportements de prospection) qu’à d’autres. Ces éléments ouvrent la voie à autant de perspectives de recherche future sur les modèles d’ambiguïté.
Appendices
Remerciements
Nous remercions deux évaluateurs anonymes pour leurs remarques pertinentes et leurs nombreuses suggestions détaillées apportées à une version préliminaire de cet article. Nous remercions également les éditeurs pour leurs indications dans le processus de révision de l’article. Ce projet a reçu le soutien financier de Rennes Métropole (AIS 2013).
Notes
-
[1]
Ellsberg, 1961, p. 657.
-
[2]
Un évènement E se définit comme un sous-ensemble de S. Dans ce qui suit, l’ensemble des conséquences possibles est noté X. Formellement, un acte – ou décision – est une application de l’ensemble des états de la nature S dans l’ensemble des conséquences X, application qui associe une conséquence de X à chaque évènement E. Dans ce qui suit, nous considérons uniquement les actes qui ont un nombre fini de conséquences. L’agent économique a des préférences sur les actes, où les notations habituelles
 ,
,  et
et  désignent la préférence faible, la préférence stricte et l’indifférence.
désignent la préférence faible, la préférence stricte et l’indifférence. -
[3]
L’ensemble C est un sous-ensemble convexe de toutes les mesures de probabilités sur l’ensemble des états de la nature (ensemble noté ∆).
-
[4]
Dans les deux cas, on suppose que l’ensemble C contient toutes les distributions de probabilités physiquement possibles.
-
[5]
Siniscalchi (2006) montre que pour l’exemple du tableau 2, si l’on suppose de plus que α = 2/3, on obtient des préférences identiques à celle d’un décideur ayant un ensemble des croyances tel que q(ER) = 1/3, q(EN) ≥ 2/9 et α = 1, preuve que α et l’ensemble des croyances C ne sont pas clairement identifiés.
-
[6]
Les scénarios sont par exemple toutes les combinaisons possibles de boules dans l’urne inconnue entre 0 et 100 : [0 rouge, 100 noires], [1 rouge, 99 noires],….[100 rouges, 0 noire]. La distribution de probabilités de second ordre peut être une distribution uniforme sur l’ensemble de ces valeurs, une distribution normale centrée sur [50 rouges, 50 noires], une loi beta de paramètres donnés… Si le décideur n’a pas pleinement confiance dans ces distributions de probabilité de second ordre, il est possible de supposer une troisième étape, avec des distributions de probabilité de troisième ordre sur les distributions de second ordre et ainsi de suite.
-
[7]
Dans un tel modèle, le décideur transforme les probabilités (non cumulatives).
-
[8]
On peut noter que, pour obtenir l’espérance d’utilité 1/3u(20), la fonction d’évaluation des actes dans Klibanoff et al. (2005) est souvent donnée par
 . ϕ–1 étant croissante, cette évaluation compare les actes comme celle donnée dans l’équation (3).
. ϕ–1 étant croissante, cette évaluation compare les actes comme celle donnée dans l’équation (3). -
[9]
La prospect theory en présence d’ambiguïté est plus large que l’utilité espérée à la Choquet et permet d’intégrer un traitement différent des gains et des pertes, non seulement en termes d’utilité, mais également en termes de poids de décision.
-
[10]
W est une capacité, c’est-à-dire que W(∅)=0, W(S)=1 et W est monotone par rapport à l’inclusion des ensembles (si Ei ⊇ Ej alors W(Ei) ≥ W(Ej) ).
-
[11]
La fonction de transformation de probabilités w est strictement croissante de [0,1] dans [0,1], avec w(0) = 0 et w(1) = 1.
-
[12]
Abdellaoui et al. (2005) et Kilka et Weber (2001) mesurent les poids de décision dans les modèles dépendant du rang à l’aide d’équivalents certains. Par exemple, l’équivalent certain z d’une décision D = ($20,E; $0Ec), où E désigne l’évolution d’un actif financier, et E son évènement complémentaire, permet d’inférer le poids de décision associé à l’évènement E. En fixant l’utilité de 0 $ à 0 et celle de 20 $ à 1, l’indifférence entre équivalent certain z et l’acte D implique : W(E)=u(z). En déterminant l’utilité de l’équivalent certain, on obtient ainsi directement le poids de décision associé à l’évènement E.
-
[13]
Grant et Polak (2013) étudient et axiomatisent l’ensemble des représentations de l’ambiguïté fondées sur un terme de moyenne (d’espérance) et sur un terme prenant en compte une mesure de l’aversion aux dispersions de l’utilité.
-
[14]
Le même argument s’applique pour le choix entre D3 et D4.
-
[15]
De manière traditionnelle, la plupart des expériences évoquées dans cet article ont été menées auprès de populations d’étudiants. Le choix d’un autre public ne modifie pas sensiblement les résultats obtenus : des expériences ultérieures ont montré que l’aversion à l’ambiguïté était présente également chez des publics aussi divers que les actuaires (Cabantous, 2007; Dupont-Courtade, 2013), les employés de compagnies d’assurance (Kunreuther et al., 1995) ou les propriétaires fonciers (Brunette et al., 2009).
-
[16]
Oechssler et Roomets (2014) passent en revue 40 études portant sur la décision en présence d’ambiguïté et aboutissent à une conclusion similaire : environ la moitié des participants auraient de l’aversion à l’égard de l’ambiguïté sur la globalité des études.
-
[17]
Dans la théorie de l’utilité espérée, le décideur est parfaitement sensible aux variations de vraisemblance.
-
[18]
Si les exemples d’Ellsberg remettent en question l’axiome d’indépendance et le principe de la chose sûre, ceux proposés par Machina (2009) remettent en cause la version affaiblie de l’axiome d’indépendance, appellée indépendance comonotone, qui est au coeur des modèles dépendant du rang.
-
[19]
L’élicitation, ou encodage, de probabilités équivalentes consiste à déterminer la probabilité objective qui rend le décideur indifférent entre une loterie fondée sur ces probabilités et un acte fondé sur un évènement simple.
Bibliographie
- Abdellaoui, M., A. Baillon, L. Placido, et P. P. Wakker (2011), « The Rich Domain of Uncertainty: Source Functions and their Experimental Implementation », American Economic Review, 101(2) : 695-723.
- Abdellaoui, M., F. Vossmann et M. Weber (2005), « Choice-based Elicitation and Decomposition of Decision Weights for Gains and Losses Under Uncertainty », Management Science, 51(9) : 1384-1399.
- Abdellaoui, M., H. Bleichrodt, E. Kemel et O. L’Haridon (2014), « Beliefs and Attitudes for Natural Sources of Uncertainty », Working paper.
- Ahn, D., S. Choi, D. Gale et S. Kariv (2014), « Estimating Ambiguity Aversion in a Portfolio Choice Experiment », Quantitative Economics, 5(2) : 195-223.
- Allais, M. (1953), « Le comportement de l’homme rationnel devant le risque : critique des postulats et axiomes de l’école américaine », Econometrica, 21(4) : 503-546.
- Baillon, A. et H. Bleichrodt (2015), « Testing Ambiguity Models Through the Measurement of Probabilities for Gains and Losses », American Economic Journal: Microeconomics, 7(2) : 77-100.
- Baillon, A., O. L’Haridon et L. Placido (2011), « Ambiguity Models and the Machina Paradoxes », American Economic Review, 101(4) : 1547-1560.
- Becker, S. W. et F. O. Brownson (1964), « What Price Ambiguity? Or the Role of Ambiguity in Decision-making », Journal of Political Economy, 72(1) : 62-73.
- Bewley, T. F. (2002), « Knightian Decision Theory : Part 1 », Decisions in Economics and Finance, 25(2) : 79-110.
- Brunette, M., L. Cabantous, S. Couture, et A. Stenger (2009), « Assurance, intervention publique et ambiguïté : une étude expérimentale auprès de propriétaires forestiers privés », Économie et Prévision, (4) : 123-134.
- Cabantous L. (2007), « Ambiguity Aversion in the Field of Insurance: Insurers’ Attitude to Imprecise and Conflicting Probability Estimates », Theory and Decision, 62(3) : 219-240.
- Camerer C. et M. Weber (1992), « Recent Developments in Modeling Preferences: Uncertainty and Ambiguity », Journal of Risk and Uncertainty, 5(4) : 325-370.
- Cerreia-Vioglio, S., F. Maccheroni, M. Marinacci et L. Montrucchio (2011), « Uncertainty Averse Preferences », Journal of Economic Theory, 146(4) : 1275-1330.
- Chateauneuf, A. et J. H. Faro (2009), « Ambiguity Through Confidence Functions », Journal of Mathematical Economics, 45(9) : 535-558.
- Chateauneuf, A. (1985), « On the Existence of a Probability Measure Compatible with a Total Preorder on a Boolean Algebra », Journal of Mathematical Economics, 14(1) : 43-52.
- Chew, S.H., B. Miao et S. Zhong (2013), « Partial Ambiguity », National University of Singapore, Working paper.
- Chow, C.C. et R. K. Sarin (2001), « Comparative Ignorance and the Ellsberg Paradox, Journal of Risk and Uncertainty, 22(2) : 129-139.
- Cohen, M., J.-Y. Jaffray et T. Said (1987), « Experimental Comparison of Individual Behavior Under Risk and Under Uncertainty for Gains and for Losses », Organizational Behavior and Human Decision Processes, 39(1) : 1-22.
- Cohen, M. et J.-M. Tallon (2000), « Décision dans le risque et l’incertain : l’apport des modèles non-additifs », Revue d’économie politique, 110(5) : 631-681.
- Conte, A. et J. D. Hey (2013), « Assessing Multiple Prior Models of Behaviour Under Ambiguity », Journal of Risk and Uncertainty, 46(2) : 113-132.
- Cubitt, R., G. van de Kuilen et S. Mukerji (2012), « Sensitivity Towards Ambiguity: A Qualitative Test and a Measurement », University of Oxford, Working paper.
- Curley, S. P., J. F. Yates et R. A. Abrams (1986), « Psychological Sources of Ambiguity Avoidance », Organizational Behavior and Human Decision Processes, 38(2) : 230-256.
- Curley, S. P. et J. F. Yates (1985), « The Center and Range of the Probability Interval as Factors Affecting Ambiguity Preferences », Organizational Behavior and Human Decision Processes, 36(2) : 273-287.
- Cyert, R. M. et M. H. DeGroot (1974), « Rational Expectations and Bayesian Analysis », Journal of Political Economy, 82(3) : 521-536.
- Dean, M. et P. Ortoleva (2012), « Allais, Ellsberg, and Preferences for Hedging », Working paper.
- Diecidue, E. et P. P. Wakker (2001), « On the Intuition of Rank-Dependent Utility », Journal of Risk and Uncertainty, 23(3) : 281-298.
- Dupont-Courtade, T. (2013), « Perception et couverture des risques extrêmes en présence d’incertitudes sur les marchés de l’assurance et de la réassurance », Thèse de doctorat, Université de Paris 1.
- Ellsberg, D. (1961), « Risk, Ambiguity, and the Savage Axioms », Quarterly Journal of Economics, 75(4) : 643-669.
- Epstein, L. G. (2010), « A Paradox for the Smooth Ambiguity Model of Preference », Econometrica, 78(6) : 2085-2099.
- Ergin, H. et F. Gul (2009), « A Theory of Subjective Compound Lotteries », Journal of Economic Theory, 144(3) : 899-929.
- Etner, J., M. Jeleva et J.-M. Tallon (2012), « Decision Theory Under Ambiguity », Journal of Economic Surveys, 26(2) : 234-270.
- Fellner, W. (1961), « Distortion of Subjective Probabilities as a Reaction to Uncertainty », Quarterly Journal of Economics, 75(4) : 670-689.
- Fox, C. R. et A. Tversky (1995), « Ambiguity Aversion and Comparative Ignorance », Quarterly Journal of Economics, 110(3) : 585-603.
- Friedman, M. et L. J. Savage (1948), « The Utility Analysis of Choices Involving Risk », Journal of Political Economy, 56(4) : 279-304.
- Frisch, D. et J. Baron (1988), « Ambiguity and Rationality », Journal of Behavioral Decision Making, 1(3) : 149-157.
- Gajdos, T., T. Hayashi, J.-M. Tallon et J.-C. Vergnaud (2008), « Attitude Toward Imprecise Information », Journal of Economic Theory, 140(1) : 27-65.
- Ghirardato, P., F. Maccheroni et M. Marinacci (2004), « Differentiating Ambiguity and Ambiguity Attitude », Journal of Economic Theory, 118(2) : 133-173.
- Gigliotti, G. et B. Sopher (1992), « The Testing Principle: A Resolution of the Ellsberg Paradox », Rutgers, The State University of New Jersey, Economics Department, Working paper.
- Gilboa, I. et M. Marinacci (2013), « Ambiguity and the Bayesian Paradigm », in D. Acemoglu, M. Arellano et E. Dekel (éds), Advances in Economics and Econometrics: Theory and Applications, Tenth World Congress of the Econometric Society, New York: Cambridge University Press.
- Gilboa, I. et D. Schmeidler (1989), « Maxmin Expected Utility with Non-Unique Prior », Journal of Mathematical Economics, 18(2) : 141-153.
- Gollier, C. (2011), « Portfolio Choices and Asset Prices: The Comparative Statics of Ambiguity Aversion », The Review of Economic Studies, 78(4) : 1329-1344.
- Grant, S. et B. Polak (2013), « Mean-Dispersion Preferences and Constant Absolute Uncertainty Aversion », Journal of Economic Theory, 148(4) : 1361-1398.
- Halevy Y. (2007), « Ellsberg Revisited: An Experimental Study », Econometrica, 75(2) : 503-536.
- Hansen, L. P. et T. J. Sargent (2001), « Robust Control and Model Uncertainty », American Economic Review, 91(2) : 60-66.
- Hansen, L. P. et T. J. Sargent (2008), « Robustness », Princeton University Press, 464 p.
- Hayashi, T. et R. Wada (2010), « Choice with Imprecise Information: An Experimental Approach », Theory and Decision, 69(3) : 355-373.
- Hey, J. D., G. Lotito et A. Maffioletti (2010), « The Descriptive and Predictive Adequacy of Theories of Decision Making Under Uncertainty/Ambiguity », Journal of Risk and Uncertainty, 41(2) : 81-111.
- Hogarth, R. M. et H. J. Einhorn (1990), « Venture Theory: A Model of Decision Weights », Management Science, 36(7) : 780-803.
- Jeleva, M. et J.-M. Tallon (2016), « Ambiguïté, comportements et marchés financiers », L’Actualité économique, à paraître.
- Kahneman, D. et A. Tversky (1979), « Prospect Theory: An Analysis of Decision Under Risk », Econometrica, 47(2) : 263-291.
- Kahn, B. E. et R. K. Sarin (1988), « Modeling Ambiguity in Decisions Under Uncertainty », Journal of Consumer Research, 15 : 265-272.
- Keynes, J. M. (1921), « A Treatise on Probability », Cambridge University Press.
- Kilka, M. et M. Weber (2001), « What Determines the Shape of the Probability Weighting Function Under Uncertainty? », Management science, 47(12) : 1712-1726.
- Klibanoff, P., M. Marinacci et S. Mukerji (2005), « A Smooth Model of Decision Making Under Ambiguity », Econometrica, 73(6) : 1849-1892.
- Knight, F. H. (1921), Risk, Uncertainty and Profit, New York : Hart, Schaffner and Marx.
- Kothiyal, A., V. Spinu et P. P. Wakker ( 2014), « An Experimental Test of Prospect Theory for Predicting Choice Under Ambiguity », Journal of Risk and Uncertainty, 48(1) : 1-17.
- Kunreuther, H., J. Meszaros, R. M. Hogarth et M. Spranca (1995), « Ambiguity and Underwriter Decision Processes », Journal of Economic Behavior and Organization, 26(3) : 337-352.
- L’Haridon, O. et L. Placido (2010), « Betting on Machina’s Reflection Example: An Experiment on Ambiguity », Theory and Decision, 69(3) : 375-393.
- Lichtenstein, S., B. Fischhoff et L. Phillips (1982), « Calibration of Probabilities: The State of the Art to 1980 », in A. Kahneman et D.Tversky (éds.), Judgement Under Uncertainty: Heuristics and Biases, New York : Cambridge University Press, chapter 22.
- Maccheroni, F., M. Marinacci et A. Rustichini (2006), « Ambiguity Aversion, Robustness, and the Variational Representation of Preferences », Econometrica, 74(6) : 1447-1498.
- MacCrimmon, K. R. et S. Larsson (1979), « Utility Theory: Axioms Versus Paradoxes », in Maurice Allais and O. Hagen, (éds.), Expected Utility Hypotheses and the Allais Paradox, p. 333-409.
- Machina, M. J. et D. Schmeidler (1992), « A More Robust Definition of Subjective Probability » Econometrica, 60(4) : 745-780.
- Machina, M. J. et M. Siniscalchi (2014), « Ambiguity and Ambiguity Aversion », Handbook of the Economics of Uncertainty, 1 : 729-807.
- Machina, M. J. (2009), « Risk, Ambiguity, and the Rank-Dependence Axioms », American Economic Review, 99(1) : 385-392.
- Marschak, J. (1975), « Personal Probabilities of Probabilities », Theory and Decision, 6 : 121-153.
- Nau, R. F. (2006), « Uncertainty Aversion with Second-Order Utilities and Probabilities », Management Science, 52(1) : 136-145.
- Neumann, J. von et O. Morgenstern (1944), Theory of Games and Economic Behavior, Princeton, NJ : Princeton University Press.
- Oechssler, J. et A. Roomets (2014), « A Test of Mechanical Ambiguity », University of Heidelberg, Department of Economics, Discussion paper series no. 555.
- Savage, L. J. (1954), « The Foundations of Statistics », New York : John Wiley & Sons.
- Schmeidler, D. (1989), « Subjective Probability and Expected Utility Without Additivity », Econometrica, 57(3) : 571-587.
- Segal, U. (1987), « The Ellsberg Paradox and Risk Aversion: An Anticipated Utility Approach », International Economic Review, 28(1) : 175-202.
- Seo, K. (2009), « Ambiguity and Second-Order Belief », Econometrica, 77(5) : 1575-1605.
- Siniscalchi, M. (2006), « A Behavioral Characterization of Plausible Priors », Journal of Economic Theory, 128(1) : 91-135.
- Siniscalchi, M. (2009), « Vector Expected Utility and Attitudes Toward Variation », Econometrica, 77(3) : 801-855.
- Slovic, P. et A. Tversky (1974), « Who Accepts Savage’s Axiom? » Behavioral Science, 19(6) : 368-373.
- Wakker, P. P. (2010), « Prospect Theory: For Risk and Ambiguity », Cambridge University Press, 518 pages.
- Wakker, P. P. (1990), « Under Stochastic Dominance Choquet-Expected Utility and Anticipated Utility are Identical », Theory and Decision, 29(2) : 119-132.
- Wald, A. (1950), « Statistical Decision Functions », Wiley.
- Yang, C.-L. et L. Yao (2014), « Testing Ambiguity Theories with a Mean-Preserving Design », Working paper.
List of tables
Tableau 1
Les paiements dans les exemples d’Ellsberg (1961)
Tableau 2
Le paradoxe à trois couleurs et les modèles à croyances multiples : illustrations
Tableau 3
Les tests des modèles d’ambiguïté