Article body

1. Introduction et problématique

L’article relate un des dispositifs de la recherche Arithmétique et Compréhension à l’École Élémentaire-ACE. L’expérimentation est réalisée en France avec des élèves de cours préparatoire (CP/première année primaire) et de cours élémentaire première année (CE1/deuxième année primaire). Notre étude porte sur la production d’écritures mathématiques produites par les élèves dans le Journal duNombre. Nous nous interrogeons sur les effets de ce dispositif pour construire le nombre et son rôle dans les apprentissages notamment pour les élèves moins avancés.

À partir des travaux de Sensevy (1996) sur le Journal des Fractions, nous formulons deux hypothèses. La première hypothèse définit l’élève moins avancé comme un élève sans mémoire et sans rapport privé aux objets de savoir, c’est-à-dire sans appétence et sans motivation. La seconde hypothèse s’intéresse au processus global d’évaluation qui semblerait déposséder l’élève moins avancé d’un rapport privé aux objets de savoir. En effet, l’évaluation ne permettrait pas à l’élève de développer une motivation intrinsèque liée à l’intérêt et au plaisir à acquérir des connaissances mathématiques.

Le dispositif étudié cherche à provoquer des retours dans les connaissances anciennes et des enquêtes vers le savoir nouveau par l’étude des écritures mathématiques produites dans le Journal du Nombre à partir des incitations du professeur ou d’un élève. L’élève dialoguerait avec son passé par la production des écritures mathématiques dans son Journal du Nombre et le passé des autres élèves lors des temps de partage. Ces échanges favoriseraient l’élaboration d’une conceptualisation partagée sur le nombre afin de mieux comprendre les mathématiques, les nombres et les signes. Nous analysons le rapport entre ce que le professeur se propose d’enseigner et ce que l’élève est susceptible d’apprendre. Nous nous interrogeons sur le rapport au savoir construit par l’élève lorsqu’il produit des écritures mathématiques dans le Journal du Nombre. Nous nous intéressons à la construction du sens et à la capitalisation du savoir.

La convention Arithmétique et Compréhension à l’École Élémentaire-ACE est signée avec la Direction générale de l’enseignement scolaire-DGESCO en mai 2010. Pour rappel, la Direction générale de l’enseignement scolaire-DGESCO a pour mission d’élaborer la politique éducative et pédagogique en France. Elle assure également la mise en oeuvre des programmes. L’expérimentation concerne les académies de Lille, Nancy, Versailles et Bretagne-Marseille pour une durée de trois ans. Nous précisons qu’une académie est une circonscription académique.

Notre étude s’inscrit dans la recherche Arithmétique et Compréhension à l’École Élémentaire-ACE. Nous commençons par évoquer brièvement les objectifs, les fondements et le rôle du Journal du Nombre dans la recherche Arithmétique et Compréhension à l’École Élémentaire-ACE afin de mieux faire comprendre notre étude.

L’objectif de la recherche Arithmétique et Compréhension à l’École Élémentaire-ACE consiste à modifier le rapport aux savoirs des professeurs pour changer le rapport au savoir des élèves. Pour cela, la recherche Arithmétique et Compréhension à l’École Élémentaire-ACE a élaboré une programmation annuelle composée de situations concrètes et complexes. Le dispositif prévoit de nombreux temps d’échanges entre l’équipe de recherche et les professeurs pour favoriser l’appropriation des contenus. Il s’agit de permettre une meilleure compréhension du réel, de la symbolisation et de l’abstraction.

Les principaux fondements de la recherche Arithmétique et Compréhension à l’École Élémentaire-ACE s’inscrivent dans la théorie des situations didactiques-TSD élaborée par Brousseau (1998). En effet, ce sont les situations proposées qui introduisent le milieu dans lequel se définissent les opérations. Les élèves enquêtent sur les petits nombres et les représentent par différentes désignations (4, c’est 2 et encore 2, c’est aussi 3 + 1 ou encore 5 - 1). Ce travail sur les petits nombres s’accompagne d’explorations dans les grands nombres. Les connaissances acquises à partir des décompositions-recompositions sur les petits nombres doivent être transférables pour le calcul des grands nombres. Par exemple, l’élève s’appuie sur la connaissance de 3 + 2 pour calculer 30 + 20. La programmation annuelle prévoit l’utilisation de différents groupements et dégroupages avant l’expérimentation de la dizaine. L’argumentation mathématique est développée par l’étude de situations itératives et évolutives.

Le Journal du Nombre dans la recherche Arithmétique et Compréhension à l’École Élémentaire-ACE favorise le dialogue entre l’équipe de recherche et les professeurs des écoles. Son rôle est d’aider à l’élaboration de connaissances mathématiques essentielles à la construction du nombre. Les échanges et les analyses doivent rendre les professeurs plus attentifs à la compréhension des situations et aux obstacles rencontrés par les élèves. La recherche Arithmétique et Compréhension à l’École Élémentaire-ACE cherche à étudier scientifiquement les problèmes d’acculturation de groupes humains à des connaissances mathématiques.

Quant à notre étude, elle s’intéresse au rapport construit par l’élève aux objets mathématiques à partir de la production des écritures dans le Journal du Nombre et notamment pour les élèves moins avancés. Le Journal du Nombre conduit-il l’élève à s’engager dans la situation pour lui permettre de faire des suggestions de solutions ? Les écritures dans le Journal du Nombre permettent-elles aux connaissances déjà-là de servir à la compréhension et à l’analyse de la situation ? L’analyse des écritures permet-elle la production de solutions provisoires ? Le Journal du Nombre permet-il à l’élève de construire une connaissance acquise qui répond à un problème après avoir vérifié les premières solutions provisoires en fonction de la cohérence interne et de l’expérimentation ? La réponse au problème étudiée dans le Journal du Nombre acquiert-elle une signification pour l’élève ?

2. Contexte théorique

Pour répondre à notre problématique, nous évoquons les travaux de Brousseau (1980) et le contrat didactique, Brousseau et Centeno (1991) sur la nécessité d’une mémoire didactique, Chevallard et Mercier (1987) avec la notion de temps didactique et d’étude, et Sensevy (1998) pour la mémoire et le temps dans la classe.

Les travaux de Brousseau (1998) portent sur le genre des interventions susceptibles d’améliorer les comportements et les connaissances mathématiques des élèves. Il élabore la théorie des situations didactiques-TSD avec les notions de contrat didactique et de dévolution. Il met en évidence les conditions sur lesquelles le professeur peut agir pour provoquer les activités et les appropriations désirées.

[D]ans une situation d’enseignement, préparée et réalisée par un maître, l’élève a en général pour tâche de résoudre un problème (mathématique) qui lui est présenté, mais l’accès à cette tâche se fait à travers une interprétation des questions posées, des informations fournies, des contraintes imposées qui sont des constantes des façons d’enseigner du maître. Ces habitudes (spécifiques) du maître attendues par l’élève et les comportements de l’élève attendus par le maître, c’est le contrat didactique.

Brousseau, 1998, p. 127

« La dévolution est l’acte par lequel l’enseignant fait accepter à l’élève la responsabilité d’une situation d’apprentissage (adidactique) ou d’un problème et accepte de lui-même les conséquences de ce transfert » (Brousseau, 1998, p. 302).

Dans la théorie des situations didactiques-TSD, il s’agit d’obtenir de l’élève la construction de la connaissance selon une démarche qui lui est propre. Une telle conception permet à la connaissance d’être perçue par l’élève comme solution du problème. Nous pouvons dire que le problème avec ses contraintes et sa situation fait partie de la signification de la notion.

Les travaux de Brousseau et Centeno (1991) montrent que les modèles erronés et les conceptions n’évoluent pas s’il n’existe pas une réorganisation intentionnelle des connaissances. Dans le système classique d’enseignement, il n’est pas prévu que quelqu’un prenne en charge l’évolution de la connaissance. On ne revient pas, on ne s’interroge pas. Toute la responsabilité est laissée à l’élève qui doit réorganiser les connaissances, corriger ses erreurs et surmonter les obstacles. Pourtant, l’apprentissage ne peut se faire qu’à partir de la continuité des différents temps d’apprentissage-enseignement et des divers statuts d’une connaissance.

« Le problème de donner du sens à ce que l’on apprend parait lié à l’établissement de connexions avec d’autres connaissances antérieures, soit parce qu’elles peuvent servir de base aux nouvelles connaissances, soit parce qu’il est nécessaire de les réorganiser pour élaborer les nouvelles connaissances »

Brousseau et Centeno, 1991, p. 13

Les travaux de Chevallard et Mercier (1987) parlent de déconcertation cognitive de l’élève dans le contrat didactique classique. La déconcertation cognitive correspond au doute, à l’opacité, au trouble et à l’incertitude en relation avec l’inachèvement des apprentissages scolaires lequel ne permet pas la construction de l’expertise. En effet, l’élève est soumis aux défilements des objets de savoir et l’activité doit faire avancer le temps didactique pour perdurer. Ainsi, s’il veut apprendre, l’élève doit pouvoir effectuer une suspension du défilement temporel qui lui permette de rencontrer et de traiter de manière privée les problèmes de la classe.

En effet, l’élève, s’il veut apprendre, doit pouvoir effectuer une suspension du défilement temporel qui lui permette de rencontrer et de traiter de manière privée les problèmes de la classe. Les travaux de Sensevy (1998) pensent une institution de la mémoire didactique dévolue aux élèves. Pour cela, il définit le travail épistémologique de l’élève comme un travail réflexif à partir de l’étude de ses propres rapports aux objets de savoir et aux objets qui lui sont inculqués. « Ce qui semble capital de faire construire à l’élève, c’est un rapport dialectique entre deux modalités de temps : l’un qui préside au rapport qui lie l’élève au temps dialectique, externe, l’autre qui est celle de son activité personnelle » (Sensevy, 1998, p. 230).

Les objets du savoir seront donc aussi des emblèmes du défilement du temps. Si l’élève reste confiné dans une position d’attente, le savoir lui restera étranger et les gestes d’étude seront interdits puisque l’élève attend du maitre les orientations et les significations.

La théorie de l’action conjointe didactique-TACD est notre cadre théorique. Nous utilisons les catégories de contrat didactique, d’action conjointe, la dialectique du contrat-milieu et celle de l’expression-réticence, le capital d’adéquation, la dévolution, les règles définitoires et stratégiques et un certain type de prise en considération des élèves moins avancés. L’action du professeur et de l’élève est conjointe puisqu’ils gagnent ou perdent ensemble au jeu d’enseignement-apprentissage. Par contrat-milieu, nous entendons les connaissances déjà-là avec lesquelles l’élève aborde la compréhension de la situation. Pour toute situation didactique, le professeur a le choix de dire ou de taire certains éléments de savoir. La dialectique de l’expression-réticence est un moyen pour le professeur de guider l’élève dans l’élaboration des connaissances. Pour être en mesure de jouer au jeu demandé, l’élève s’appuie sur des connaissances anciennes. Le professeur cherche à rendre l’élève capable de mobiliser les éléments de savoir par la dévolution du milieu. Dans le jeu d’apprentissage, les règles définitoires sont les règles qui permettent de jouer et les règles stratégiques sont celles qui permettent de gagner. Enfin, les élèves hors-jeu sont, pensons-nous, des élèves trop éloignés du savoir. De ce fait, ils ne peuvent tirer profit des échanges du collectif.

2.1 Origine du Journal du Nombre

L’élève est toujours agent, presque jamais auteur dans le contrat didactique classique. Quant au savoir, il est un savoir-temps qui dévolue à l’élève la dialectique du temps institutionnel et la durée personnelle de l’élève dans un contrat didactique. Pour remédier à cela, Sensevy (1998) pense le Journal des Fractions. Il construit les catégories d’emblèmatisation et de chronogénéité. L’emblèmatisation doit permettre à l’élève de dialoguer avec son propre passé et celui des autres élèves. La chronogénéité doit instituer l’élève comme un apprenti de l’enseignant. À partir de ce constat, une ingénierie de l’interaction entre la durée personnelle de l’élève et le temps institutionnel est pensée. Le dispositif doit être susceptible de montrer les productions d’élèves comme des phénomènes de cette interaction. Les écritures mathématiques produites doivent montrer la durée personnelle de l’élève et le temps institutionnel (les connaissances et les programmes) pour une possible théorie interprétative de la temporalité à l’école élémentaire, c’est-à-dire comment les élèves construisent différemment les connaissances étudiées. Nous listons les effets attendus du Journal des Fractions dans le tableau ci-dessous.

Tableau 1

Effets attendus du Journal des Fractions

Effets attendus du Journal des Fractions

-> See the list of tables

La spécificité de l’ingénierie du Journal des Fractions était greffée sur une transposition didactique classique au plan des fractions. Pour atteindre les effets espérés, le travail et l’étude dans le Journal des Fractions étaient conçus sur le temps long, une année scolaire et même davantage. Un système commun de significations et la constitution d’une mémoire didactique était l’enjeu de la recherche. Il était destiné à être modifié en fonction de l’évolution de la théorie et des insuffisances constatées. En 2011, dans quatre académies, une ingénierie coopérative s’occupe de créer des modèles et de réaliser des dispositifs d’enseignement pour la conception de situations, leur conduite et leur analyse. L’ingénierie tente de modifier le dispositif par l’implémentation de la progression Arithmétique et Compréhension à l’École Élémentaire-ACE. Il s’agit de la mise en place d’un curriculum afin de réorganiser les mathématiques pour en faciliter l’accès et l’efficacité.

3. Méthodologie

Chaque élève possède un Journal du Nombre dans lequel il écrit des mathématiques à partir d’une incitation. Cela consiste pour le professeur à faire travailler par la classe la nature du travail spécifique qui va être produit. La classe étudie collectivement les enjeux de l’incitation avec la stratégie des essais et erreurs. Les écrits à partir de l’incitation du professeur sont des productions de première génération qui correspondent à des premiers jets sur un problème spécifique. En effet, les travaux dans le Journal du Nombre montrent les rapports que l’élève entretient avec les objets mathématiques et sa compréhension du contrat didactique. Sous l’impulsion du professeur et plus tard de l’élève lui-même, des travaux sont affichés, explicités, analysés et détournés. La comparaison de plusieurs productions alimente l’enquête sur le savoir. Ensuite, l’élève est invité à poursuivre l’enquête dans son Journal du Nombre, en s’inspirant de l’étude des travaux partagés. Plus tard, le professeur sélectionne certaines productions de première génération. Ce sont des premiers jets qui peuvent devenir des modèles à suivre du savoir en jeu. À partir du questionnement sur les productions partagées, l’élève travaille à nouveau dans le Journal du Nombre. Ce sont les productions de seconde génération, des seconds jets issus du partage et de la confrontation. Le professeur choisit parmi ces productions de seconde génération celles qui permettent de résoudre un problème ou de répondre à une question. Ces productions sont étudiées et soumises à la discussion. Elles peuvent devenir des emblèmes du savoir.

Nous faisons le choix d’exclure du Journal du Nombre tout processus global d’évaluation. Le support choisi n’induit pas un rapport présupposé aux mathématiques. Il est composé uniquement de pages blanches. Il devrait renforcer l’autonomie de l’élève, son autodétermination à produire des modèles à suivre. L’élève peut y penser librement le nombre et ses différentes représentations à partir de l’incitation du professeur. L’élève va pouvoir enquêter sur des objets mathématiques avec une motivation intrinsèque. La production d’écritures attestera de la capitalisation du savoir.

Chaque jour, les travaux sont datés. Nous pouvons ainsi situer la production de l’élève à l’intérieur de la situation et de la programmation. Nous pensons favoriser la dévolution du milieu à l’élève par l’enquête sur des objets de savoir complexes. Les travaux de l’élève sont à la source de l’avancée du temps didactique. Nous encourageons les parenthèses et gardons les essais. Le partage des productions et les échanges permettront l’enseignement-apprentissage dans la temporalité de l’élève. Le changement de la nature du contrat didactique s’élaborera par l’action conjointe. Nous rappelons que notre étude porte sur le type de rapport au savoir construit par l’élève dans le Journal du Nombre et l’analyse de la capitalisation du savoir. L’incitation du professeur doit aider l’élève à mobiliser les connaissances déjà-là. La monstration des écritures produites, le partage et les échanges favoriseront l’exploration de la situation et le dépassement des connaissances déjà-là. L’absence d’évaluation devrait libérer les essais, les erreurs, les productions d’écriture, les exemples, les modèles à suivre et les emblèmes. Ce sont les questions issues du milieu par l’incitation du professeur qui engageront l’enquête.

Notre dispositif, pour fonctionner, doit instituer les échanges autour des productions de l’élève comme une pratique de classe ordinaire. Le visualiseur projette la production de l’élève sur le tableau blanc numérique. La monstration à toute la classe permet l’élaboration de règles pour une entente conjointe nécessaire à l’étude des travaux. Les échanges construisent la mémoire didactique collective. Le partage et les échanges sont indispensables à l’action conjointe. Les différents temps élaborent une conceptualisation partagée du nombre.

3.1 Sujets

Le texte est écrit à la première personne du pluriel en référence à la posture de chercheur-professeur. L’auteur est à la fois un chercheur de l’équipe Arithmétique et Compréhension à l’École Élémentaire-ACE et le professeur d’une classe de cycle deux. La posture de chercheur-professeur nous semble pouvoir rendre compte de la complexité de la pratique et de la relation entre celui qui produit des connaissances scientifiques (chercheur) et celui qui les utilise (le professeur dans la classe). Nous cherchons à élaborer un système de référentiels partagés par l’élève, le professeur et le chercheur afin d’inscrire le singulier à la fois dans les modèles d’apprentissage et les matrices théoriques.

La recherche s’est effectuée dans une école élémentaire française d’une ville de 50 000 habitants, située près du centre-ville et à proximité d’un quartier défavorisé représentant 30 % de l’effectif global du groupe scolaire. L’école comprend huit classes réparties en cinq classes élémentaires et trois classes maternelles. Les 189 élèves représentent 150 familles. Les élèves filmés pour notre étude sont majoritairement des élèves de cycle deux (cycle des apprentissages fondamentaux) et sont âgés de six, sept ou huit ans. La recherche se déroule sur plusieurs années scolaires consécutives. Elle concerne 120 élèves lors de la phase-test et 91 lors de l’application. Les parents, les élèves et les professeurs de l’équipe de l’école sont régulièrement informés de l’avancée de la recherche.

Lors de la réunion de début d’année, le chercheur-professeur présente la recherche Arithmétique et Compréhension à l’École Élémentaire-ACE. Il informe les parents sur le droit à l’image et sollicite leurs accords pour filmer les élèves lors des séances de mathématiques.

3.2 Instrumentation

Nous cherchons à comprendre pourquoi l’élève écrit ce qu’il écrit dans le Journal du Nombre et les effets sur le rapport au savoir. Le choix d’enregistrer toutes les séances de mathématiques sur plusieurs années scolaires constitue une base de données conséquente. Nous sélectionnons pour notre étude le semestre deux de l’année deux. Les transcriptions des vidéos sont réalisées à partir du logiciel Transana. Ce logiciel possède une interface ergonomique de quatre fenêtres qui comprend la vidéo, la visualisation du son, la transcription et la base de données. La segmentation des vidéos en unité de codage est réalisée par le biais de mots-clés choisis dans les concepts de la théorie de l’action conjointe en didactique-TACD. Ces mots-clés définissent ensuite les épisodes didactiques sélectionnés. La constitution de collections est réalisée par le regroupement d’extraits de vidéos de même nature créées à partir d’une transcription limitée par deux codes temporels.

3.3 Déroulement

La recherche Arithmétique et Compréhension à l’École Élémentaire-ACE est une recherche longitudinale sur trois années scolaires avec un prolongement prévu nommé ArithmEcole. Notre recherche se situe lors de l’année deux. Le chercheur-professeur accompagne les élèves du cours préparatoire (CP/première année primaire) au cours élémentaire première année (CE1/deuxième année primaire). Le terrain de recherche est constitué par six élèves de cours préparatoire (CP/première année primaire) et dix-huit élèves de cours élémentaire première année (CE1/deuxième année primaire). Les élèves de cours élémentaire (CE1/deuxième année primaire) construisent le nombre avec le Journal du Nombre pour la seconde année consécutive. Nous rappelons que nous cherchons à comprendre le rapport aux objets mathématiques construit par l’élève dans le Journal du Nombre. Nous présentons le dispositif de la recherche Arithmétique et Compréhension à l’École Élémentaire-ACE pour mieux situer notre étude et notre dispositif d’enregistrement.

Tableau 2

Étapes du dispositif de filmage

Étapes du dispositif de filmage

-> See the list of tables

3.4 Méthode d’analyse des données

Nous choisissons d’étudier les effets du Journal du Nombre à des temps différents de l’année 2 de l’enseignement-apprentissage à partir des catégories d’emblèmatisation et de chronogénéité pour en comprendre les effets sur le rapport au savoir.

Le temps zéro correspond à une production d’élève dans le Journal du Nombre faisant état de connaissances sur les petits répertoires additifs.

Le temps un montre l’émergence des connaissances déjà-là avec lesquelles l’élève peut aborder la situation. L’élève mobilise ce qu’il comprend de la situation avec l’ancien contrat. L’élève est mis en situation de dialoguer avec son passé et le passé des autres élèves à partir de l’étude de l’incitation.

Le temps deux est constitué par l’enquête mathématique, l’appropriation de l’incitation et la recherche du nouveau contrat. L’étude des règles définitoires alimente la production des écritures mathématiques pouvant devenir des modèles à suivre. L’exploration du nouveau contrat-milieu s’effectue à partir des propositions des élèves. L’élève devient l’apprenti du professeur et est amené à jouer le bon jeu.

Le temps trois est composé du partage des analyses de travaux produits de seconde génération, dans le Journal du Nombre. Ce sont des productions d’élève qui répondent à un problème ou à une question. Elles peuvent constituer des emblèmes du savoir.

Le temps quatre est un dépassement des éléments de savoir, une reconstruction des connaissances acquises.

Notre étude porte sur les écrits des élèves et notamment sur les écrits des élèves moins avancés réalisés dans le Journal du Nombre dans la classe du chercheur-professeur. Nous définissions succinctement ce que nous entendons par « élève moins avancé ». C’est un élève qui hésite à prendre la parole dans la classe pour faire avancer le temps didactique. Il s’exprime peu lors de l’élaboration des savoirs collectifs. Il est en position d’attente. L’élève moins avancé possède des connaissances qu’il peine à mobiliser pour affronter la situation. Nous pouvons dire que l’élève moins avancé agit avec un contrat didactique classique.

Pour notre étude, nous sélectionnons deux élèves moins avancés de cours élémentaire première année (CE1/deuxième année primaire), Marthe et Jean. Nous retenons également une élève avancée de cours préparatoire (CP/première année primaire), Anne. Ces trois élèves appartiennent à la classe de CP/CE1 dont l’effectif est de 24 élèves. Ces productions doivent nous aider à comprendre pourquoi et comment les élèves produisent ce qu’ils écrivent dans le Journal du Nombre. Nous analysons les productions de Marthe, Jean et Anne. La monstration des écritures mathématiques construit le temps de l’enseignement-apprentissage. Les échanges à partir des productions créent la chronogénéité. Nous décrivons brièvement les profils des trois élèves.

Marthe est une élève joyeuse. Elle dit volontiers qu’elle n’aime pas les mathématiques et qu’elle n’y comprend rien. Elle reste souvent en retrait. Jean fait des propositions qui sont régulièrement hors de la situation. Quant à Anne, élève de cours préparatoire (CP/première année primaire), elle sait construire des liens entre les connaissances étudiées.

3.5 Considérations éthiques

Afin de garantir l’anonymat des participants, nous modifions les prénoms des élèves. L’académie et le laboratoire de rattachement du chercheur-professeur ne sont pas précisés. Le formulaire pour le consentement des parents les informe que la loi fait obligation, avant toute publication de l’image d’une personne, de recueillir son accord explicite ou celui de ses représentants légaux. Les enregistrements et les images produites seront réservés à la formation des professeurs, et destinés à des personnels de l’éducation, de la formation ou de la recherche (voir formulaire en annexe).

4. Résultats

L’échantillon est constitué des productions de Marthe et Jean, élèves moins avancés de cours élémentaire première année (CE1/deuxième année primaire) et des travaux de Anne, élève de cours préparatoire (CP/première année primaire). L’extrait du Journal du Nombre de Jean montre les connaissances déjà-là au temps zéro. La photographie du tableau de la classe illustre le temps un, celui de l’incitation avec le temps de l’étude collective de l’incitation. L’extrait de la transcription représente le temps deux. Il s’agit de questions posées par Marthe et Jean lors de l’enquête. Nous analysons ensuite les représentations du nombre avec l’abaque. Il s’agit de productions de première et seconde génération, premiers et seconds jets lors des temps trois et quatre. L’ensemble des différents temps représente dix séances.

Nous décrivons la situation. L’élève doit représenter un nombre ≤ 6 à l’aide d’une décomposition ou d’une opération (un calcul) en deux termes. Le nombre à représenter est obtenu par un lancer de dé. La situation est fondée sur les connaissances des petits répertoires additifs comme 1 + 1 = 2, 4 – 2 = 2 ou 5 – 3 = 2 pour explorer la numération de position. Le même nombre peut être désigné par différentes décompositions. L’enjeu consiste à trouver un moyen d’agrandir la décomposition.

L’élève produit des énoncés de problèmes (des opérations) c’est-à-dire des décompositions qui représentent, pour notre exemple, le nombre deux. L’élève envisage le milieu-problème avec les connaissances déjà-là, c’est-à-dire la connaissance des répertoires additifs. La situation est adidactique puisque l’intention d’enseigner la numération de position n’est pas explicite. Elle engage l’élève à prendre des décisions, à engager des stratégies pour trouver un moyen économique de désigner le même nombre à partir de l’agrandissement d’une même décomposition.

Figure 1

Journal du Nombre de Jean et les connaissances déjà-là

-> See the list of figures

Au temps zéro, la production de Jean montre un élève avec des connaissances sur le nombre dix. Ces connaissances déjà-là pourraient permettre à Jean d’envisager la nouvelle situation. Pourtant au temps un, la seule décomposition qu’il produit est 1 + 1 = 2. Pour Jean, le temps d’enquête, le temps 2 semble être une nécessité afin de pouvoir jouer au jeu demandé avec un contrat adéquat. Les autres désignations proposées dans la classe sont les suivantes : 10 – 8 = 2, 1 – 1 = 2 (proposition rejetée), 4 – 2 = 2, 3 – 1 = 2, 11 – 9 = 2, 8 – 6 = 2, 5 – 3 = 2 et 12 – 2 = 10 (proposition rejetée). La classe rencontre un milieu-problème qui consiste en comment agrandir la décomposition-calcul ? Après un temps de réflexion, quelques élèves murmurent que cela n’est pas possible. Le silence perdure quelques instants. Les échanges débutent avec la proposition que 100 – 98, c’est 2. L’argument développé par l’élève, en faveur du nombre deux, consiste à prouver que 98 + 2 font 100. Un autre élève s’empare de la proposition précédente et il la modifie. Il produit l’écriture suivante 1000 – 998 = 2 parce que 998 + 2, c’est 1000. La comparaison des décompositions 100 – 98 et 1000 – 998 amène l’enquête sur la numération de position. Peut-on proposer, pour le nombre deux, une nouvelle décomposition à partir de l’étude de la comparaison des nombres 100 et 98 avec 1000 et 998 ? Un élève propose 10 000 – 9998. Plusieurs élèves ne sont plus d’accord. Il semblerait que ce soit beaucoup trop. La grandeur des nombres pose problème. Comment des nombres aussi grands pourraient-ils désigner un si petit nombre ? Pourtant, quelques élèves affirment que cela est tout à fait possible puisque la décomposition proposée comporte deux grands nombres. D’autres élèves ajoutent que l’on enlève presque tout, c’est-à-dire que le second nombre (9998) est presque aussi grand que le premier (10 000). L’enquête consiste à rechercher des critères pour valider ou invalider la décomposition-calcul. La comparaison du nombre de chiffres, cinq chiffres pour 10 000 et quatre chiffres pour 9998, confirme la grandeur et la proximité des nombres.

Figure 2

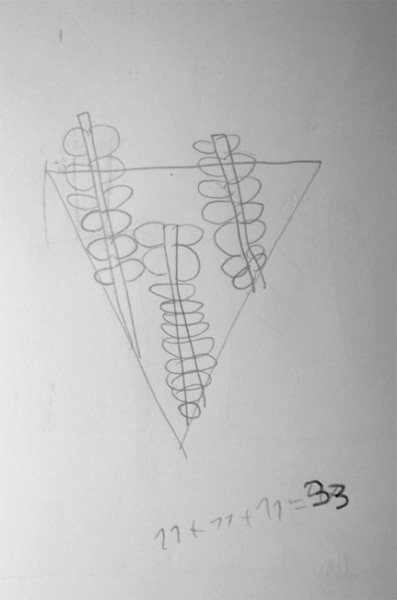
Tableau de la classe lors de l’incitation collective productive

-> See the list of figures

Sur la photographie, nous voyons un élève jouant avec le nombre deux et la numération de position. Comment aider les élèves moins avancés à produire des écritures conformes au jeu demandé par le professeur dans le Journal du Nombre à partir de leurs connaissances déjà-là ? Pour cela, le chercheur-professeur oriente l’enquête lors d’une nouvelle séance sur la représentation du nombre à partir des abaques. Nous décrivons brièvement l’objet. Il se compose d’un socle rectangulaire sur lequel sont emboitées trois tiges verticales. L’outil possède trente-trois bouchons identiques. Chacune des tiges a une valeur croissante de droite à gauche (unités, dizaines, centaines). Les bouchons positionnés sur les tiges aident à différencier la quantité de la valeur. Chaque élève reçoit un abaque et 33 bouchons. Le chercheur-professeur choisit de taire les règles définitoires, celles qui définissent la valeur de chaque tige. Il demande à l’élève de représenter un nombre sur l’abaque. Il choisit d’attirer l’attention de l’élève sur le nombre restreint de bouchons en taisant la valeur des tiges. Le milieu constitué par l’abaque est similaire à notre système de numération qui comporte un nombre restreint de chiffres à partir desquels il est possible d’écrire tous les nombres. Le chercheur-professeur a anticipé la proposition du nombre trente-trois par l’élève. Nous montrons les travaux de Marthe et de Jean dans le Journal du Nombre. Nous verrons ensuite comment le milieu va apporter des rétroactions.

Figure 3

Journal du Nombre de Marthe et les abaques

-> See the list of figures

Figure 4

Journal du nombre de Jean et les abaques

-> See the list of figures

Marthe et Jean ont réparti équitablement les bouchons sur chacune des tiges de l’abaque et produit l’écriture additive 11 + 11 + 11 = 33. La description de l’abaque va permettre d’entrer dans la définition des règles définitoires et d’agir dans le milieu. Nous montrons un court extrait de la transcription lors de l’enquête. La classe se questionne au sujet de l’abaque.

Le bref échange montre que les élèves dialoguent avec leur passé et le passé des autres élèves. Certains élèves anticipent le rôle des tiges : « La tige des unités … elle peut être vide ? » (tdp 8) et « Comment écrire des grands nombres … comme 1000 … l’abaque a trois tiges » (tdp 3), tandis que Marthe pense « que l’on ne peut écrire que des petits nombres » (tdp 2). Le chercheur-professeur choisit de demander aux élèves de représenter un nombre de leur choix dans le Journal du Nombre. Il sollicite différents travaux d’élève pour élaborer conjointement les règles définitoires. Les productions affichées et discutées au sein de la classe amènent au partage des connaissances. Les élèves vont s’approprier les règles définitoires du fonctionnement de l’abaque et comprendre la lecture (codage-décodage) des grands nombres par l’enquête sur les nombres représentés dans les productions. L’étude des productions de Marthe et Jean place l’élève au centre des investigations.

Figure 5

Journal du Nombre de Anne et les abaques, élève de cours préparatoire (CP)

-> See the list of figures

La production de Anne, élève de cours préparatoire (CP/première année primaire) fait avancer le temps didactique parce qu’elle représente un nombre à trois chiffres sur deux tiges. Il s’agit du nombre 143 avec 14 dizaines et 3 unités. La tige des dix possède quatorze bouchons avec une croix sur le dixième bouchon. Ce repère posé par Anne est une aide au comptage de dix en dix pour comptabiliser le juste nombre de dizaines. La croix signifie une centaine que l’élève représente avec dix groupes de dix. La production de l’élève de cours préparatoire (CP/première année primaire) permet de confronter deux écritures du nombre 143 (10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 1 + 1 + 1 avec 100 + 10 + 10 + 10 + 10 + 1 + 1 + 1).

Figure 6

Journal du Nombre de Jean et les problèmes

-> See the list of figures

Considérons maintenant le travail de Jean dans le Journal du Nombre, au temps trois. Il s’est donné trois problèmes et représente les nombres 157, 128 et 203. Ce sont des nombres à trois chiffres. On remarque qu’il cherche à appliquer les règles définitoires en prenant appui sur le milieu constitué des trois tiges. En effet, il produit différents codages. Il écrit 1 c = 100 (tige des centaines), 5d = 50 (tige des dizaines) et 7. Pour terminer, il ajoute l’écriture additive 100 + 50 + 7 = 157. La connaissance de l’abaque comme outil pour calculer déjà présente est maintenant associée aux règles définitoires et accroit la capitalisation de savoir. Observons maintenant le travail de Marthe.

Figure 7

Journal du Nombre de Marthe et les problèmes

-> See the list of figures

Marthe se donne les problèmes 100, 128 et 203. Elle choisit d’écrire le nombre de bouchons sous chaque tige. Cela produit deux types écritures. Un calcul pour le nombre 128 qui est formé de 100 + 20 + 8 = 128 et des décompositions pour les nombres 203 et 100 (203 + 0 = 203 et 100 + 0 = 100). Observons l’écriture 203 + 0 = 203 et le codage réalisé à partir de l’abaque. L’élève a placé deux bouchons sur la tige des centaines et trois bouchons sur la tige des unités. Elle a donc représenté le nombre 203 avec 2 centaines et 3 unités. Sous l’abaque, elle écrit le chiffre des centaines (2), le chiffre des dizaines (0) et le chiffre des unités (3) qu’elle code 203 + 0. Pour la décomposition 100 + 0, l’écriture et la représentation de l’abaque concordent puisque la tige des centaines est la seule à posséder un bouchon. La lecture d’un nombre à partir de l’abaque s’appuie maintenant sur la connaissance des règles définitoires. Marthe peut lire et écrire de grands nombres. Les productions dans le Journal du Nombre montrent une capitalisation de savoir avec un rapport au savoir différent de celui de Jean.

Nous montrons une production de Jean dans le Journal du Nombre au temps quatre, le temps du dépassement et de l’autodétermination. L’élève joue à partir d’une décomposition à explorer la numération de position. À partir de la connaissance des petits répertoires tels que 4 + 1 = 5, l’élève produit le calcul 40 + 10 = 50 puis 400 + 100 = 500 et enfin 4000 + 1000 = 5000. La production des écritures montre une capitalisation et une reconstruction de savoir.

Figure 8

Journal du Nombre de Jean et les écritures mathématiques

-> See the list of figures

5. Discussion des résultats

Nous cherchions à répondre à plusieurs questions. Comment les élèves moins avancés écrivent-ils ce qu’ils écrivent dans le Journal du Nombre et quel est le rapport construit par l’élève aux objets mathématiques ? Les productions partagées du Journal du Nombre devaient montrer que l’élève est un apprenti de l’enseignant (chronogénéité) et représenter des emblèmes de savoir.

Pour cela, nous avons soumis à l’étude un petit échantillon de productions issues du Journal du Nombre lors de l’année deux. Marthe et Jean, élèves moins avancés de cours élémentaire première année (CE1/deuxième année primaire), possèdent des connaissances mathématiques qu’ils ne mobilisent pas ou peu pour répondre à la situation. Néanmoins, les travaux de Marthe et de Jean sont une source d’activité pour la classe. Quant à la production d’Anne, elle permet aux élèves de dialoguer avec leur passé et le passé des autres élèves pour approfondir le savoir. La monstration et le partage participent à l’avancée du temps didactique. Les productions n’ont donc pas seulement constitué un support pour un dialogue maitre-élève mais également un dialogue élève-élève. Certains élèves pouvaient transmettre la pertinence qu’ils expérimentaient dans leur travail et qu’ils avaient construite. D’autres élèves pouvaient se renforcer de la pertinence qu’ils avaient atteinte et qu’ils pouvaient à leur tour transmettre. La chronogénéité s’est construite à partir de l’étude des productions. Les mêmes significations partagées ont élaboré une culture commune de l’enquête et du nombre. Le travail sur la mémoire des situations a construit les emblèmes.

Nous avons montré que le Journal du Nombre est un dispositif qui permet de relier le temps institutionnel et la durée personnelle de l’élève. Dans notre exemple, l’enquête sur les nombres de 0 à 1 000 et l’étude de la numération de position sont menées par l’élève. Le Journal du Nombre lui permet de discuter avec son passé, les connaissances déjà-là et celui des autres élèves par la confrontation des différents travaux. Le partage des connaissances participe à l’évolution des représentations de tous les élèves et notamment des élèves moins avancés. Le fait d’exclure du Journal du Nombre toute évaluation, nous a permis, pensons-nous, d’assurer à l’élève moins avancé un rapport privé aux objets mathématiques. Une future piste de recherche pourrait consister à comparer un Journal du Nombre non évalué (notre étude) avec un Journal du Nombre évalué afin de poursuivre l’analyse du rapport privé aux objets de savoirs.

Le Journal du Nombre un est dispositif d’enseignement-apprentissage par lequel l’élève construit un rapport aux objets de savoir dans sa propre temporalité. La recherche de la compréhension du contrat-milieu procure à l’élève la rencontre avec les connaissances déjà-là à partir desquelles il va pouvoir voir ou entendre ce qui lui est accessible lors de l’incitation et du partage des écritures mathématiques. L’action conjointe dépend de la construction de cet arrière-plan. Les nouveaux échanges permettent à l’élève de se mettre en disponibilité intellectuelle pour l’étude du concept mathématique. Parmi ses productions, l’élève travaille dans sa durée personnelle, dans sa mémoire et dans la mémoire du système didactique que constitue la classe. Dans ses productions figurent des éléments qui pourront être utilisés par la classe pour avancer dans le temps didactique. Les enquêtes sont une aide au partage de connaissances. L’étude des productions écrites construit l’agir ensemble. Les fondamentaux de la progression Arithmétique et Compréhension à l’École Élémentaire-ACE participent également à la chronogénéité. Le Journal du Nombre est un outil pour conceptualiser les mathématiques mais ce dispositif pour fonctionner doit être pensé avec le report de l’évaluation. Le Journal du Nombre est à envisager sur l’année scolaire ou sur plusieurs années.

Les recherches de Brousseau et Centeno (1991) montrent que dans le contrat didactique classique le professeur peut fonctionner sans mémoire. En effet, il n’existe pas d’institution spécifique sur le travail, l’étude et la reprise par l’élève lui-même. L’élève ne revient pas sur ses connaissances et ses rapports aux objets institutionnels. De plus, une grande part de la gestion des connaissances est laissée aux élèves. Avec l’incitation et le Journal du Nombre, les élèves moins avancés conçoivent des rapports plus épistémologiques à la mémoire et au temps. En effet, le processus d’emblèmatisation permet aux élèves moins avancés d’accéder au savoir et de reconstruire de nouvelles connaissances. Ces derniers ont alors une place dans l’avancée du travail de la classe et perçoivent les profits symboliques de la forme scolaire.

6. Conclusion

Nous rappelons que nous cherchions à analyser le rapport au savoir construit par l’élève avec le Journal du Nombre. Nos hypothèses définissaient l’élève moins avancé comme un élève sans mémoire, sans rapport privé aux objets de savoir, sans motivation intrinsèque et dépossédé d’un rapport privé aux objets de savoir par le processus global d’évaluation. Par la production des écritures mathématiques dans le Journal du Nombre, l’élève devient le moteur de l’avancée du temps didactique. Il prend la responsabilité de l’enquête. L’étude des productions partagées est en étroite relation avec la chronogénéité. Les échanges participent ainsi à l’avancée du temps didactique. L’étude des productions permet de relier la dialectique du temps institutionnel, la programmation des savoirs et la durée personnelle de l’élève. La chronogénéité ne peut exister sans l’émergence d’un autre contrat didactique dans lequel l’élève est l’apprenti du professeur. Le Journal du Nombre et les enquêtes sur les objets de savoir élaborent les mathématiques comme des sciences expérimentales. Le Journal du Nombre a vocation à devenir un outil dont les modèles à suivre et les emblèmes puissent être utilisables pour la théorie et la formation.

La limite de notre étude concerne le travail des élèves hors-jeu. Ce sont des élèves trop éloignés du savoir qui produisent peu d’écrits et ne peuvent tirer profits des échanges de la classe. Notre recherche se centre actuellement sur « le comment » amener les élèves hors-jeu à produire des écritures dans le Journal du Nombre. Le groupe d’anticipation, nouveau dispositif complémentaire au Journal du Nombre, consiste à faire travailler avec le professeur un petit groupe d’élèves de niveaux hétérogènes sur des connaissances anciennes. Nous nous intéressons aux connaissances qui sont nécessaires aux élèves hors-jeu pour tirer profit des échanges dans la classe. Nous cherchons comment faire mieux réussir les élèves qui échouent habituellement. Le dispositif du groupe d’anticipation serait susceptible de procurer aux élèves hors-jeu « par contagion » le capital informationnel qui leur manque pour garantir l’élaboration d’écritures mathématiques et de connaissances.