Abstracts
Résumé
Focalisé sur les indicateurs physico-chimiques soutenant la biologie des cours d’eau, l’article examine l’interpolation de ce type de mesures, dans le temps et l’espace, pour le calcul des indices légaux requis par la Directive Cadre Européenne sur l’Eau. En effet, le calcul d’indicateurs statistiques, à partir d’une information très lacunaire, pose problème. Différentes méthodes de calcul du quantile 90 par station sont-elles équivalentes? Comment cet indicateur varie-t-il spatialement? Le Réseau National de Bassin français fournit-il suffisamment d’information pour une caractérisation pertinente de la qualité des eaux?
Les sorties du modèle déterministe ProSe appliqué à la Seine, à pas de temps journalier, sont utilisées pour comparer différentes méthodes de calcul des indicateurs. Les résultats déduits du modèle exhaustif sont comparés à ceux calculés après un échantillonnage simulant celui du réseau de surveillance.
Deux calculs du quantile 90 temporel par station sont examinés : le calcul classique fondé sur la fonction de quantile empirique, et une méthode légèrement plus complexe, avec une pondération temporelle et une linéarisation de la fonction de quantile, qui atténue effectivement les biais induits par l’échantillonnage irrégulier durant l’année, ou découlant du nombre restreint de mesures.
Trois méthodes de « spatialisation » sont ensuite testées afin d’obtenir des pourcentages d’occurrence des quantiles par classe de qualité dans chaque « Masses d’Eau Cours d’Eau » : le « principe de défaillance » retient la station la plus défavorable; la deuxième méthode calcule la proportion des stations par classe de qualité; la dernière pondère chaque station par son « segment d’influence ». La spatialisation par segments d’influence des quantiles temporels au sein des « Masses d’Eau Cours d’Eau » améliore nettement les estimations des pourcentages d’occurrence, montrant la nécessité de la prise en compte de la localisation des stations lors du calcul d’un indice de qualité.
Mots-clés :
- Directive Cadre sur l’Eau,
- indicateurs physico-chimiques,
- quantile 90,
- Masses d’Eau Cours d’Eau,
- estimation,
- incertitude,
- simulation,
- spatialisation
Abstract
This research aimed to understand how to interpolate discrete measurements, in space and time, in order to calculate physico-chemical indicators in rivers, which are required by the European Water Framework Directive. Linked to this issue, several questions were addressed. Are the different methods used to calculate temporal 90th-percentiles at a given site equivalent? How does this legal indicator vary in space? Does the French National Basin Network provide enough information to make consistent water quality characterization?
The daily outputs of the ProSe model applied to the Seine River were used as proxies to compare different calculation methods of the 90th-percentile. The results deduced from the exhaustive model were compared to those calculated, after sampling the outputs according to the monitoring network sampling scheme. Two calculations of the temporal 90th-percentile at a given site were examined: the classical method based on the empirical percentile function and a slightly more complex method that includes temporal weighting and linearization of the empirical percentile function. This second method reduced the estimation bias of the 90th-percentile induced by irregular and/or few measurements.
Three methods for spatializing the 90th-percentiles were tested to obtain occurrence percentages of the percentiles for each quality class in each “Stream Water Body”: the “failure principle” consists in keeping only the worst site; the second approach calculates the proportion of sites located in each quality class; the third method allocates an influence segment to each measurement site. Spatializing temporal percentiles in “Stream Water Bodies” by influence segments led to a marked improvement in occurrence percentage estimations and revealed the need to take into account the spatial configuration of measurement sites when calculating a quality indicator.
Keywords:
- Water Framework Directive,
- physico-chemical indicators,
- 90th-percentile,
- Stream Water Bodies,
- estimation,
- uncertainty,
- simulation,
- spatialization
Article body
1. Introduction
En réponse à la préoccupation internationale concernant la qualité des eaux, le parlement européen adopte la Directive Cadre sur l’Eau (DCE) le 23 octobre 2000. Celle-ci vise à préserver la qualité des eaux ou à en restaurer le bon état écologique à l’horizon 2015 (INERIS, 2005). Dans une étape préalable de caractérisation, la DCE préconise le découpage des eaux superficielles et souterraines européennes en unités d’évaluation nommées « masses d’eau », chaque pays étant responsable de la délimitation de ses « masses d’eau ». En France, les « masses d’eau » se rapportant aux eaux continentales de surface, et plus particulièrement aux rivières ou tronçons de rivières, sont dites « Masses d’Eau Cours d’Eau » ou MECE. Elles ont été délimitées selon un critère d’homogénéité biologique et physico-chimique du milieu (Site du Sandre, 2008).
En attendant les classes de qualité uniformisées en Europe – annoncées pour 2009 –, l’état de ces MECE est actuellement caractérisé selon le Système français d’Évaluation de la Qualité des cours d’eau (SEQ-Eau). Ayant défini seize types d’altération de la qualité physico-chimique de l’eau, et recensé les différents indicateurs impliqués, le SEQ-Eau définit cinq classes de qualité (excellent, bon, moyen, mauvais, et très mauvais état) pour chacun d’eux (Site de l’Ifremer, 2009). L’appartenance à une classe de qualité est déterminée par la valeur d’un critère statistique : la moyenne si l’on s’intéresse aux indicateurs biologiques, et le quantile 90 (c’est-à-dire la valeur dépassée dans 10 % des cas) pour les indicateurs physico-chimiques, par exemple.
Dans ce travail, cinq « indicateurs physico-chimiques soutenant la biologie » sont considérés (nitrates NO3-, ammonium NH4+, orthophosphates PO43-, oxygène dissous O2d, et matières en suspension MES), pour lesquels l’indice recommandé par la DCE est le quantile 90 annuel, en vertu de la sensibilité du milieu naturel aux pics de concentration. En effet, on cherche à estimer les pourcentages d’occurrence et les concentrations d’épisodes de pollution, qui, même de courte durée, peuvent se révéler très nuisibles pour l’écosystème.
Il a été montré (Bernard-Michel et de FOUQUET, 2005; Bernard-Michel, 2006) que, par station de mesure, le calcul de ce quantile était très biaisé et très imprécis à partir de prélèvements peu nombreux (moins d’une mesure par mois) ou préférentiels durant l’année (six mesures en hiver et douze en été, par exemple). Or, la qualité des eaux françaises est surveillée par le Réseau National de Bassin français (RNB), avec généralement dix à douze mesures annuelles par station.
Nous tentons de répondre aux questions pratiques posées par le calcul d’un indice statistique (moyenne, quantile) à partir d’une information très lacunaire : comment le quantile 90 temporel varie-t-il spatialement? Quelle est l’influence de la méthode de calcul sur les indices de qualité obtenus par MECE? Les mesures du RNB sont-elles suffisantes pour caractériser adéquatement l’état des eaux?
Afin de répondre à ces interrogations, une portion du réseau hydrographique de la Seine a été choisie comme site d’étude (Figure 1). Pour les masses d’eau correspondantes, nous disposons des mesures aux stations du RNB, ainsi que d’autres mesures hebdomadaires et d’un modèle déterministe qui en simule le fonctionnement écologique. L’idée est d’exploiter la résolution spatio-temporelle très fine des sorties du modèle pour connaître la « qualité réelle » des MECE, et ainsi déterminer le calcul d’indice de qualité le plus adéquat à partir des mesures effectivement disponibles.
Figure 1
Réseau modélisé par ProSe et localisation des 27 stations du RNB.
Hydrographic network modeled by ProSe and location of 27 RNB measurement sites.
Le modèle ProSe (Evenet al., 1998, 2004, 2007; Flipoet al., 2004, 2007) est composé de trois modules complémentaires : hydrodynamique, transport et biogéochimie. Le module hydrodynamique est basé sur une formulation longitudinale monodimensionelle des équations de Saint-Venant, résolues par différences finies (Hug, 1975). Le module de transport simule l’advection et la dispersion des substances conservatives et réactives, qu’elles soient dissoutes ou particulaires. Le module biogéochimique consiste en une adaptation du modèle RIVE (Billenet al., 1994; Garnieret al., 1995).
Plus de 300 km de la Seine, complétés par quelques dizaines de kilomètres de la Marne à l’amont de sa confluence avec la Seine (Figure 1) sont simulés. ProSe fournit des concentrations instantanées et ponctuelles en différentes substances – dénommées « valeurs ProSe » – au pas de temps de 20 minutes et au pas d’espace de 500 mètres environ, i.e. avec un maillage spatio-temporel très fin en comparaison des données disponibles.
Avant d’utiliser les « valeurs ProSe » pour tester un calcul d’indice de qualité, deux vérifications sont nécessaires.
La première consiste à comparer visuellement, pour chacune des stations de mesure, les mesures disponibles au pas mensuel et les résultats du modèle ProSe à midi, à la date du prélèvement (Figure 2 : exemple de la station 10). Cette comparaison entre mesures et résultats de ProSe effectuée pour l’ensemble des stations de mesure nous donne une première indication sur la validité du modèle ProSe comme outil de simulation du fonctionnement biogéochimique de la Seine.
Figure 2
Comparaison des chroniques fournies par ProSe et mesurées par le RNB pour les différents indicateurs. Exemple de la station 10.
Comparison of simulated (ProSe) and measured (RNB) time series for all considered indicators. Example of measurement site 10.
La seconde vérification porte sur la variabilité temporelle au pas de temps hebdomadaire. L’objectif est de s’assurer que la variabilité temporelle des résultats de ProSe est réaliste. Le variogramme temporel des valeurs ProSe échantillonnées à pas hebdomadaire est comparé à celui d’un deuxième ensemble de mesures, au pas de temps hebdomadaire, également disponible sur le domaine. Cette variabilité sera testée pour des intervalles de une à cinq semaines (Figure 3). Malgré des écarts notables, notamment pour les orthophosphates (PO43-) et les matières en suspension (MES), la concordance de ces variogrammes est jugée suffisante pour valider le modèle ProSe au pas hebdomadaire.
Figure 3
Comparaison de la variabilité à petit pas de temps des différents indicateurs simulés par ProSe et mesurés par le RNB. Variogrammes temporels simples et croisés des valeurs instantanées, calculés à pas hebdomadaire, à Suresnes.
Comparison of spatial variability for short time steps of simulated (ProSe) and measured indicators at a given location (Suresnes).
Nous supposerons enfin que la variabilité infra-hebdomadaire des différents indicateurs est également reproduite par ProSe de façon suffisamment réaliste. Ce point a été vérifié pour l’oxygène dissous, variable pour laquelle des mesures au pas de temps 15 minutes sont disponibles (Poulin, 2006), et lors d’études spécifiques locales (Martin, 2001).
Ce qui précède nous conduit à utiliser les résultats de ProSe pour constituer une population statistique de référence. Cet ensemble dit « de référence » est constitué des valeurs journalières calculées à midi pour toutes les mailles de calcul, au pas de 500 mètres environ.
Le deuxième ensemble de valeurs est un sous-échantillonnage des résultats de ProSe au droit des stations du RNB et aux dates de mesure. Deux ensembles de données issus des valeurs ProSe sont donc disponibles : la « référence », au pas de temps journalier et au pas de 500 mètres, et l’échantillonnage (spatial et temporel) de ces valeurs aux lieux et dates des mesures du RNB.
Dans la suite, seule la réalité ProSe est désormais considérée, afin de comparer les résultats de différentes méthodes de calcul à une référence parfaitement connue. L’échantillonnage RNB n’intervient plus qu’à travers le lieu et la date des mesures. Deux méthodes de calcul du quantile 90 temporel, et trois méthodes de spatialisation de ce quantile à partir de l’échantillonnage RNB sont comparées, et les écarts par rapport à la « référence ProSe » sont examinés. La précision des indicateurs actuels est ainsi quantifiée empiriquement.
La DCE préconise l’attribution d’un unique indice de qualité à chaque MECE. Pour une étude détaillée des performances des indicateurs, nous préférons indiquer ici un pourcentage d’occurrence spatial dans chaque classe de qualité afin de mettre en évidence la variabilité de l’indice temporel au sein d’une MECE. Le pourcentage d’occurrence de référence est égal à la proportion de points appartenant à chaque classe de qualité. À partir de l’échantillonnage ProSe, le quantile temporel est d’abord calculé par station puis spatialisé selon différentes méthodes, afin d’attribuer un pourcentage d’occurrence dans chaque classe de qualité.
Une étude de sensibilité au nombre de stations par MECE complète cette étude.
2. Site d’étude : la seine
Le site d’étude comporte 225 km de cours d’eau le long de la Seine, dont environ 14 km à l’amont de sa confluence avec la Marne, et 36 km le long de la Marne (Figure 1). Les limites amont sur la Seine et sur la Marne se situent approximativement à l’entrée de la région parisienne. La longueur totale de la Seine passant par cette grande région urbanisée est d’environ 80 km. La partie centrale du bassin versant de la Seine est constituée des plaines agricoles de l’Île-de-France, parmi les plus fertiles du territoire français, et de vastes forêts domaniales et privées entourant l’agglomération parisienne. Cette dernière concentre 10 millions d’habitants, soit environ 60 % de la population du bassin versant de la Seine sur moins de 2 % de sa surface. Les efforts accomplis depuis de nombreuses décennies en matière de collecte et de traitement des eaux usées industrielles et urbaines ont permis d’améliorer considérablement la qualité de l’eau de la Seine. Avec un débit moyen de 500 m3•s-1 et un débit d’étiage de 200 m3•s-1, la capacité de dilution du fleuve Seine est limitée, ce qui contraint les riverains à des niveaux élevés d’épuration de leurs rejets par temps sec et pose de plus le problème des rejets de temps de pluie lorsque le réseau de collecte ne permet plus d’acheminer la totalité des eaux ruisselées vers les stations d’épuration.
La caractérisation objective de la qualité de l’eau de ce système fortement impacté, soumis à des apports polluants hautement variables, présente un intérêt majeur pour les scientifiques et les gestionnaires.
Le modèle ProSe a été mis en oeuvre pour simuler la qualité de l’eau des années récentes, bien documentées, parmi lesquelles l’année 2003, sur laquelle cette étude se concentre.
3. Méthodes
3.1 Les méthodes de calcul du quantile 90 temporel
Le quantile k d’une population est défini comme la valeur α telle que k % de la population lui sont inférieurs, Z désignant le « paramètre » et x la localisation considérés :
Dans cet article, seul le quantile 90 est considéré.
Pour l’oxygène dissous, c’est le « quantile 90 après classement des valeurs par ordre décroissant » qui a été considéré (ce qui est équivalent, en statistique, au quantile 10). En effet, contrairement aux autres indicateurs considérés, une MECE est en bon état pour des concentrations élevées en oxygène dissous.
Nous présentons ici deux méthodes de calcul du quantile 90 temporel.
3.1.1 Méthode classique
Pour le calcul du quantile 90 temporel, chaque agence de l’eau utilise actuellement sa propre méthode, essentiellement basée sur les dires d’experts. Nous retenons ici comme « méthode classique » le calcul fondé sur les statistiques classiques. En chaque station, le quantile 90 temporel est obtenu par inversion de la fonction de quantile empirique, qui est une fonction en escalier. En pratique, les n valeurs mesurées durant l’année sont classées par ordre croissant (deux mesures identiques comptant comme deux valeurs différentes). Le quantile 90 est alors la valeur de rang i tel que ![]() , ce qui revient à attribuer un poids égal à 1/n à chaque mesure. Par exemple, avec n = 11 mesures dans l’année, le quantile 90 est la valeur de rang i tel que
, ce qui revient à attribuer un poids égal à 1/n à chaque mesure. Par exemple, avec n = 11 mesures dans l’année, le quantile 90 est la valeur de rang i tel que ![]() , soit i = 10. Après classement par ordre croissant, l’avant-dernière valeur est retenue comme quantile 90.
, soit i = 10. Après classement par ordre croissant, l’avant-dernière valeur est retenue comme quantile 90.
3.1.2 Méthode améliorée
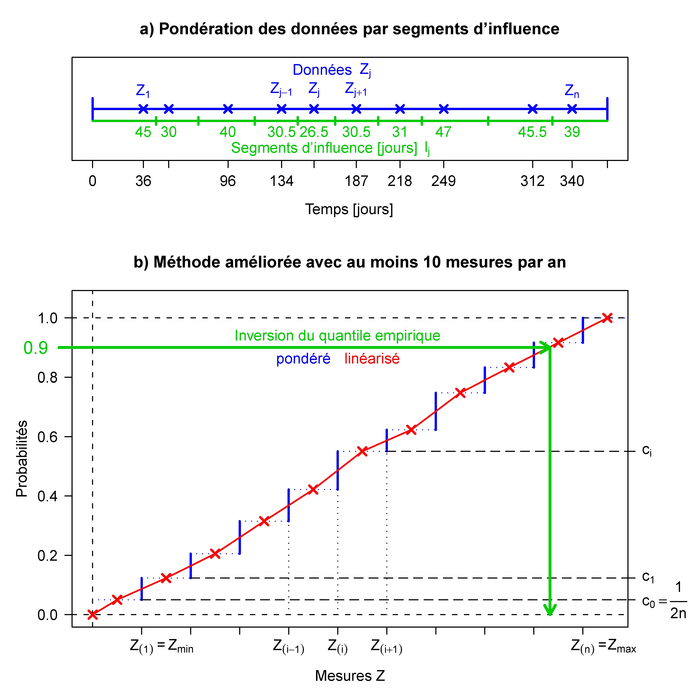
Ce calcul par station peut être amélioré pour tenir compte des irrégularités et des lacunes de l’échantillonnage temporel (Bernard-Michel, 2006). La « méthode améliorée » comprend deux étapes illustrées par la figure 4.
Figure 4
P rincipe de calcul du quantile 90 selon la " méthode améliorée ". a) Définition des segments d'influence àpartir des mesures. b) Pondération et linéarisation du quantile empirique; Z(i) désigne la valeur de rang i, aprèsclassement des mesures Zj par ordre croissant.
Principle of the 90-percentile calculation by the "improved method". a) Definition of influence segments frommeasurements. b) Weighting and linearizing the empirical quantile; Z(i) denotes the value of rank i after orderingthe measurements Zj by increasing order.
Tout d’abord, les données sont pondérées par des segments d’influence qui représentent la « durée d’influence » de chaque point. Les limites des segments sont les dates de début et de fin de l’année considérée, ainsi que les médiatrices entre dates de mesures consécutives. Le poids de chacune des n mesures ne vaut plus 1/n, mais est égal à la longueur de son segment d’influence rapportée à l’année considérée. La pondération par segments d’influence revient à une simplification du krigeage temporel qui suffit, en pratique, pour des calculs à une dimension (Bernard-Michel et de FOUQUET, 2005). Cette pondération temporelle permet d’atténuer les effets des lacunes ou du caractère préférentiel de l’échantillonnage temporel (Équation 2). La fonction de quantile empirique est calculée à partir des données pondérées, puis linéarisée par morceaux (Équations 3 et 4).
Remarque : afin de diminuer le biais dû au faible nombre de mesures (le quantile étant une statistique basée sur la loi des grands nombres), la fonction de linéarisation permet de fixer arbitrairement un minimum et maximum auxquels un segment d’influence de longueur nulle est associé. En l’absence de bornes spécifiées par l’utilisateur, le minimum est fixé à 0 et le maximum est ici calculé arbitrairement à partir du plus grand écart observé entre deux valeurs successives supérieures à la médiane : ![]() .
.
Cependant, le nombre de mesures étant ici supérieur ou égal à 10 pour toutes les stations, les minima et maxima n’interviennent pas dans le calcul du quantile 90, qui s’obtient de la façon suivante :
où 
Si la « méthode classique » présente le grand avantage d’être simple et donc facilement applicable par tout acteur de la qualité de l’eau, elle n’en présente pas moins plusieurs inconvénients auxquels la « méthode améliorée » permet de remédier, moyennant une mise en oeuvre un peu plus complexe. C’est par exemple le cas des données irrégulières (échantillonnage préférentiel, lacunes, etc.) ou peu nombreuses, pour lesquelles les biais importants induits par la « méthode classique » sont réduits par la « méthode améliorée » (Bernard-Michel, 2006).
3.2 Méthodes de spatialisation des quantiles 90
Afin d’attribuer, par MECE, un pourcentage d’occurrence des quantiles 90 dans chaque classe de qualité, il est nécessaire de spatialiser les quantiles calculés aux stations du RNB. En d’autres termes, les quantiles 90 obtenus aux stations du RNB doivent être étendus à l’ensemble de la MECE. Nous proposons trois méthodes de spatialisation de complexité croissante (Figure 5), applicables quel que soit l’ordre ou la méthode de calcul du quantile considéré.
Figure 5
L es différentes méthodes de spatialisation des quantiles 90 pour obtenir les pourcentages d'occurrence dans chaque classe de qualité.
Different methods to spatialize the 90-percentiles in order to attribute occurrence percentages to each quality class.
La première méthode, fondée sur un « principe de défaillance », étend à toute la masse d’eau le quantile 90 le plus défavorable des stations de cette masse d’eau; elle est dite « méthode pénalisante » (Figure 5a).
En référence aux calculs statistiques usuels, la seconde méthode attribue un même poids à toutes les stations d’une masse d’eau, qu’elles soient proches ou éloignées : c’est la « méthode équi-pondérée ». Le pourcentage d’occurrence dans une classe de qualité est égal à la proportion de stations (dans la MECE considérée) pour lesquelles le quantile 90 appartient à cette classe (Figure 5b).
Enfin, la « méthode pondérée » généralise la pondération par segment d’influence. Un segment d’influence (une longueur d’influence, cette fois) est associé à chaque station, afin d’intégrer la distance – variable – entre stations au calcul du pourcentage d’occurrence par classe de qualité. Le pourcentage d’occurrence dans une classe de qualité est alors égal à la longueur totale des segments d’influence appartenant à cette classe divisée par la longueur de la MECE (Figure 5c).
Remarque : Une pondération spatio-temporelle pourrait être définie pour des stations irrégulièrement espacées et des mesures non nécessairement synchrones. Cette généralisation n’a pas été examinée.
4. Résultats et discussion
Le modèle ProSe est utilisé comme maquette pour tester le calcul du quantile 90 temporel proposé par Bernard-Michel (2006) et sa spatialisation. À partir de l’échantillonnage ProSe, qui reproduit l’échantillonnage aux stations du RNB, les résultats obtenus par les deux méthodes de calcul, « méthode classique » et « méthode améliorée » (cf. § 3.2), sont comparés et confrontés aux quantiles calculés à l’aide de la population (au sens statistique d’ensemble de valeurs) de référence des valeurs ProSe (pas journalier, pas d’espace 500 mètres). Les quantiles 90 calculés selon la « méthode améliorée » sont toujours spatialisés suivant la « méthode pondérée » (cf. § 3.3). Par souci de clarté, la « méthode améliorée pondérée » est simplement désignée comme « méthode améliorée » dans la suite (Figure 6 ).
Figure 6
M éthodes de calcul du quantile 90 et de spatialisation de cequantile.
Methods to calculate 90-percentile and to spatialize it.
4.1 onfrontation visuelle des résultats
Les illustrations se présentent de manière identique pour toutes les variables. Les pourcentages d’occurrence sont indiqués pour chacune des classes du SEQ-Eau, illustrées par les couleurs conventionnelles (bleu : excellent état, vert : bon état, jaune : état moyen, orange : mauvais état, rouge : très mauvais état, selon les limites de classes réglementaires). Afin de visualiser la variabilité spatiale du quantile 90 au sein d’une MECE, les limites des six MECE concernées sont matérialisées par des lignes verticales tout au long du domaine modélisé. Les lignes verticales en tirets représentent les limites amont de chacune des deux MECE situées respectivement sur la Marne et sur la Seine à l’amont de leur confluence (cf. Figure 1). Cette dernière correspond à la première ligne verticale continue (cf. Figure 7, pk ˜ 650).
Figure 7
Caractérisation de l'état des eaux selon le SEQ-Eau pour les nitrates; les pourcentages 'occurrence des quantiles 90 temporels dans chaque classe de qualité sont indiqués par MECE, élimitées suivant les pk (km).
Characterization of water quality according to SEQ-Eau system for nitrates; occurrence ercentages of 90-percentiles in each quality class are given for each "Stream Water Body", defined according to the pk (km).
Pour chaque classe de qualité, le pourcentage d’occurrence obtenu par la « méthode classique équi-pondérée » est indiqué en noir, et celui fourni par la « méthode améliorée » en vert, le pourcentage d’occurrence de référence étant reporté en bleu.
Pour les nitrates (Figure 7), tous les quantiles 90 temporels se situent dans une même classe de qualité, et affichent une très faible variabilité spatiale. La « méthode classique équi-pondérée » ainsi que la « méthode améliorée » fournissent un pourcentage d’occurrence égal au pourcentage de référence.
Pour les paramètres variant de manière significative sur le domaine, tels l’ammonium, l’oxygène dissous et les matières en suspension, les résultats sont quelque peu différents.
Pour l’ammonium, les pourcentages d’occurrence calculés via la « méthode améliorée » sont généralement plus proches des pourcentages de référence (Figure 8a). C’est par exemple le cas de la MECE la plus en aval : selon la « méthode classique équi-pondérée », 33 % de la MECE présentent un très mauvais état écologique, contre 48 % suivant la « méthode améliorée », alors que le pourcentage d’occurrence de référence dans cette classe de qualité est de 45 %. Le gain de précision de la « méthode améliorée » n’est donc pas négligeable par rapport à la « méthode classique équi-pondérée ».
Figure 8
Caractérisation de l'état des eaux selon le SEQ-Eau pour : (a) l'ammonium, et (b) l'oxygène dissous; les pourcentages d'occurrence des quantiles 90 temporels dans chaque classe de qualité sont indiqués par MECE, délimitées suivant les pk (km).
Characterization of water quality according to SEQ-Eau system for (a) ammonium and (b) dissolved oxygen; occurrence percentages of 90-percentiles in each quality class are given for each "Stream Water Body", defined according to the pk (km).
La même observation peut être effectuée globalement pour l’oxygène dissous, les écarts entre les pourcentages d’occurrence obtenus par les méthodes « classique » et « améliorée » étant toutefois moindres (Figure 8b).
Cette observation est également valable pour les matières en suspension, lorsque le quantile 90 ne varie que légèrement au sein de la MECE (Figure 9a). Dans le cas contraire, c’est la « méthode classique équi-pondérée » qui fournit des pourcentages d’occurrence plus proches des pourcentages de référence.
Figure 9
Caractérisation de l'état des eaux selon le SEQ-Eau pour : (1) les matières en suspension, et (b) les orthophosphates; les pourcentages d'occurrence des quantiles 90 temporels dans chaque classe de qualité sont indiqués par MECE, délimitées suivant les pk (km).
Characterization of water quality according to SEQ-Eau system for (a) suspended matter and (b) orthophosphates; occurrence percentages of 90-percentiles in each quality class are given for each "Stream Water Body", defined according to the pk (km).
Pour les orthophosphates, l’allure générale du quantile 90 de référence est relativement bien approchée par les deux méthodes, et il en est de même des pourcentages d’occurrence par classe de qualité (Figure 9b).
Cependant, aucune de ces deux méthodes ne reproduit correctement les changements de classe du quantile 90. Or, ce sont justement ces changements de classe, jusqu’alors déterminés principalement par expertise, qu’il est important de positionner le plus fidèlement possible par rapport à la réalité. La « méthode améliorée » fournit toutefois des pourcentages d’occurrence plus proches de la référence, ce qui témoigne de l’intérêt de cette méthode par rapport à la « méthode classique ».
Cette première analyse montre donc que les résultats sont analogues (NO3-), ou quand ils sont différents (NH4+, O2d, PO43-, MES), c’est globalement la « méthode améliorée » qui donne des pourcentages d’occurrence plus proches de la référence.
4.2 Confrontation quantitative des résultats
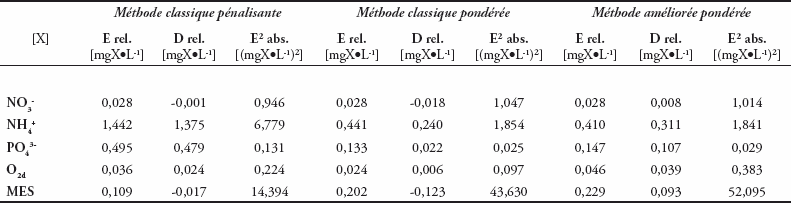
Afin d’affiner l’analyse, le tableau 1 présente la comparaison quantitative des quantiles 90 obtenus à l’aide des deux méthodes de calcul par rapport au quantile de référence. Outre les différences par rapport à la référence, ce tableau reprend également les écarts (valeur absolue des différences) relatifs au quantile 90 de référence ainsi que les écarts quadratiques absolus.
Ces statistiques sont calculées en moyenne sur tout le domaine. Pour garantir la pertinence de la comparaison, les quantiles calculés par les deux méthodes sont spatialisés, étant donné le faible nombre de stations par MECE. Si les quantiles calculés à l’aide de la « méthode améliorée pondérée » sont connus en tout point via les segments d’influence spatiaux, ce n’est pas le cas des quantiles fournis par la « méthode classique », uniquement disponibles aux stations. Deux méthodes de spatialisation de ces derniers quantiles ont été testées : la « méthode pénalisante » et la « méthode pondérée » (cf. Figure 5).
La comparaison des deux premières colonnes (« méthode classique pénalisante » vs. « méthode classique pondérée ») permet de juger de l’importance de la spatialisation des quantiles 90, tandis que la confrontation des deux dernières (« méthode classique pondérée » vs. « méthode améliorée pondérée ») traduit l’influence de la pondération des données et de la linéarisation de la fonction de quantile empirique.
Toutes variables confondues, la « méthode pondérée » donne généralement de meilleurs résultats en matière d’écart au quantile de référence, même si l’amélioration reste modeste lorsque la « méthode pénalisante » fournit déjà de faibles écarts. C’est, par exemple, le cas des nitrates, variable qui, rappelons-le, fluctue peu sur le domaine. En revanche, pour des indicateurs présentant une forte variabilité spatiale, tels que l’oxygène dissous, les orthophosphates ou l’ammonium, les écarts relatifs sont plus importants, et l’apport de la « méthode pondérée » devient plus tangible : les écarts sont réduits d’un ordre de grandeur. Pour l’ammonium, par exemple, l’écart relatif moyen égal à 145 % avec la « méthode classique pénalisante », ne vaut plus que 14 % avec la « méthode classique pondérée » (cf. Tableau 1).
Tableau 1
É carts relatifs (E.rel.), différences relatives (D.rel.) et écarts quadratiques absolus (E².abs.) moyens entre quantiles 90 calculés et quantiles de référence
Table 1. Average relative deviations (E. rel), relative differences (D. rel) and absolute squared deviations (E². abs.) between calculated and reference 90-percentiles.
Ces observations montrent la grande importance de la spatialisation des indices temporels.
Pour les matières en suspension, les quantiles 90 sont plus proches des quantiles de référence lorsqu’ils sont calculés par la « méthode classique pénalisante ». Ceci pourrait s’expliquer par la dynamique contrastée des matières en suspension, qui présentent une concentration faible la plupart du temps, mais des concentrations très élevées épisodiquement, notamment lors d’événements pluvieux. Pour que le quantile 90 calculé soit représentatif du quantile de référence, il faudrait que ces épisodes aient été échantillonnés, ce qui n’est pas nécessairement le cas avec une seule mesure par mois – la fréquence d’échantillonnage moyenne du RNB. Dès lors, contrairement à la « méthode pondérée », qui combine des quantiles 90 (temporels) sous-estimés lorsqu’un épisode n’a pas été échantillonné, la « méthode pénalisante », qui retient le quantile 90 le plus dégradant, a plus de chances de se rapprocher du quantile de référence, ce dernier étant influencé par de plus nombreux pics de concentrations.
Enfin, les écarts par rapport à la référence obtenus respectivement à l’aide des méthodes « classique » et « améliorée » présentent approximativement le même ordre de grandeur. Les matières en suspension mises à part, c’est généralement la « méthode classique » qui fournit des écarts légèrement plus faibles.
En conclusion, ces résultats quantitatifs montrent l’adéquation de la « méthode pondérée » pour la spatialisation du quantile 90. Bien que la « méthode améliorée » soit théoriquement la mieux adaptée (Bernard-Michel, 2006), l’amélioration induite par la linéarisation et la pondération du quantile empirique n’est pas flagrante ici, du fait de la régularité de l’échantillonnage temporel du RNB – malgré quelques lacunes. Avec dix mesures ou plus par an, l’irrégularité des dates de prélèvement (ce qui n’est pas le cas pour les stations retenues et l’année 2003) engendre des conséquences beaucoup plus graves sur le calcul du quantile que leur effectif réduit. La pondération apparaît donc plus importante que la linéarisation.
Cette analyse montre également l’importance de la localisation spatiale des stations, avec comme corollaire la nécessité de spatialiser les quantiles 90.
Par ailleurs, la forte variabilité spatiale de certains quantiles 90 temporels mérite d’être notée étant donné le critère d’homogénéité sur lequel est basé le découpage des MECE. Un découpage évolutif des MECE est-il envisageable, pour s’adapter à l’apparition ou à la disparition de singularités? La station d’épuration Seine Aval, par exemple, mériterait d’être considérée comme une discontinuité en raison de la variation abrupte des concentrations en ammonium, oxygène dissous et orthophosphates qu’elle provoque (cf. Figures 8 et 9b, pk ˜ 720 km).
4.3 Sur un réseau moins informé
Le RNB étant particulièrement dense aux alentours de Paris sur le domaine modélisé par ProSe, il est intéressant de se ramener au cas d’un réseau plus clairsemé, plus proche des conditions habituelles de calcul d’un indice de qualité d’une MECE. La plupart des masses d’eau ne comportant en effet qu’une ou deux stations informées mensuellement, nous avons arbitrairement « écarté » la moitié des stations du domaine d’étude.
Le tableau 2 présente les moyennes des différences, des écarts et des écarts quadratiques obtenus à partir de ce réseau moins informé, pour les deux méthodes de calcul du quantile 90 (« classique » et « améliorée ») et pour deux méthodes de spatialisation (« pénalisante » et « pondérée », cf. Figure 5).
Tableau 2
Écarts E, différences D, et écarts quadratiques E2 moyens entre quantiles 90 calculés et quantiles de référence en conservant une station du RNB sur deux.
Table 2. Average relative deviations (E. rel), relative differences (D. rel) and absolute squared deviations (E². abs.) between calculated and reference 90-percentiles when considering half of the measurement sites.
Concernant le calcul du quantile 90 temporel aux stations, les méthodes « classique » et « améliorée » fournissent des résultats quasiment semblables et très proches de la référence, qui s’expliquent comme précédemment par la régularité temporelle des mesures.
Par rapport à l’échantillonnage spatial effectivement disponible, la dégradation des résultats est sensible, excepté pour la « méthode classique pénalisante », qui fournit des écarts très semblables à ceux obtenus en considérant toutes les stations. La suppression de la moitié des stations de mesures augmente considérablement les écarts à la référence, notamment pour l’ammonium et les orthophosphates; autrement dit, augmenter le nombre de stations de mesures peut modifier sensiblement les résultats. Par exemple, par rapport au quantile de référence, l’écart relatif moyen du quantile 90 d’ammonium obtenu avec la « méthode classique pondérée » est de 44 % en considérant une station sur deux (cf. Tableau 2), contre 14 % avec la totalité des stations (cf. Tableau 1). Pour l’ammonium et les orthophosphates, les écarts sont nettement plus réduits en spatialisant par la « méthode pondérée » plutôt que par la « méthode pénalisante ». Ainsi, l’écart relatif moyen du quantile 90 d’orthophosphates (par rapport au quantile de référence), qui vaut 50 % avec la « méthode pénalisante », est réduit à 13 % en spatialisant selon la « méthode pondérée ». Dans une moindre mesure, cette méthode de spatialisation permet également d’atténuer l’écart relatif moyen du quantile 90 d’oxygène dissous (par rapport au quantile de référence).
En revanche, c’est encore une fois l’inverse pour les matières en suspension, la « méthode pénalisante » conduisant à des quantiles 90 plus proches de la référence.
La méthode de spatialisation a peu d’influence sur les quantiles 90 de nitrates, ces derniers étant très peu variables.
5. Conclusion
Deux méthodes de calcul du quantile 90 temporel ont été comparées, une « méthode classique » et une « méthode améliorée », cette dernière permettant de prendre en compte un pas d’échantillonnage variable des observations.
Différentes méthodes de spatialisation des quantiles 90 temporels ont été testées pour tenter de reconstituer au mieux l’évolution spatiale des indicateurs le long d’un cours d’eau. Sur le domaine étudié, la « méthode pondérée » conduit le plus souvent à des écarts par rapport à la référence sensiblement inférieurs à ceux de la « méthode pénalisante ». Cette méthode (« méthode pondérée ») peut être de plus améliorée (« méthode améliorée ») pour tenir compte d’éventuelles irrégularités de l’échantillonnage (Bernard-Michel, 2006).
Par ailleurs, sur la portion de réseau hydrographique modélisée par ProSe, le quantile 90 temporel fluctue entre différentes classes de qualité à l’intérieur de certaines MECE comprenant plusieurs sites de surveillance de la qualité de l’eau. Or, la DCE demande de caractériser chaque MECE par un indice unique de qualité. Se pose alors la question de l’indice à choisir pour synthétiser cette information spatiale. Faut-il retenir la moyenne spatiale de tous les quantiles temporels d’une MECE, ou la moyenne temporelle des quantiles spatiaux de cette MECE, ces deux résultats étant généralement différents? Une autre possibilité serait d’appliquer le « principe de défaillance » en calculant un quantile spatio-temporel sur l’ensemble des données disponibles pour une masse d’eau.
Finalement, il serait également possible de calculer, pour chaque masse d’eau, des pourcentages d’occurrence dans les différentes classes de qualité, cette information étant plus riche de sens qu’un unique indice par MECE. L’évolution historique d’une masse d’eau perturbée pourrait alors être suivie, afin de caractériser la diminution de son taux de défaillance par rapport au bon état ou au très bon état au fur et à mesure que des travaux destinés à améliorer sa qualité seraient réalisés. Il a été montré que ces pourcentages sont mieux évalués (par rapport à la référence exhaustive) s’ils sont calculés par la « méthode améliorée » consistant en une pondération spatiale, qui est d’autant plus sensible que les quantiles 90 sont variables au sein d’une MECE.6. Remerciements
Appendices
Remerciements
Les auteurs expriment leur gratitude au Syndicat Interdépartemental d’Assainissement de l’Agglomération Parisienne (SIAAP), au Service de Navigation de la Seine (SNS), ainsi qu’au Syndicat des Eaux d’Île-de-France, pour la mise à disposition des données nécessaires à ce travail.
Bibliographie
- Références bibliographiques
- BERNARD-MICHEL C. et C. de FOUQUET (2005). Geostatistical indicators of waterway quality for nutrients. Dans : VIIth Congress of Geostatistics, 26 septembre-1 octobre 2004, Banff, Alberta, Canada. Compte rendu n°2, pp. 907-912.
- BERNARD-MICHEL C. (2006). Indicateurs géostatistiques de la pollution dans les cours d’eau. Thèse de Doctorat, spécialité géostatistique, ENSMP, 161 p.
- BILLEN G., J. GARNIER et P. HANSET (1994). Modelling phytoplankton development in whole drainage networks: the RIVERSTRAHLER model applied to the Seine river system. Hydrobiologia, 289, 119-137.
- EVEN S., M. POULIN, J. GARNIER, G. BILLEN, P. SERVAIS, A. CHESTERIKOFF et M. COSTE (1998). River ecosystem modeling: application of the PROSE model to the Seine River (France). Hydrobiologia, 373/374, 27-45.
- EVEN S., M. POULIN, J.-M. MOUCHEL, M. SEIDL et P. SERVAIS (2004). Modelling oxygen deficits in the Seine river downstream of combined sewer overflows. Ecol. Model., 173, 177-196.
- EVEN S., J.-M. MOUCHEL, P. SERVAIS, N. FLIPO, M. POULIN, S. BLANC, M. CHABANEL et C. PAFFONI (2007). Modeling the impacts of Combined Sewer Overflows on the river Seine water quality. Sci. Total Environ., 375, 140–51.
- FLIPO N., S. EVEN, M. POULIN, M.-H. TUSSEAU-VUILLEMIN, T. AMEZIANE et A. DAUTA (2004).Biogeochemical modelling at the river scale: plankton and periphyton dynamics (Grand Morin case study, France), Ecol. Model., 176, 333-347.
- FLIPO N., C. RABOUILLE, M. POULIN, S. EVEN, M.-H. TUSSEAU-VUILLEMIN et M. LALANDE (2007). Primary production in headwater streams of the Seine basin: the Grand Morin river case study. Sci. Total Environ., 375, 98-109.
- GARNIER J., G. BILLEN et M. COSTE (1995). Seasonal succession of diatoms and chlorophycae in the drainage network of the river Seine: observations and modelling. Limnol. Oceanogr., 40, 750–765.
- HUG M. (1975). Mécanique des fluides appliquées: aux problèmes d’aménagement et d’énergétique.Eyrolles (Éditeur), Paris, France, pp. 1185-1195.
- MARTIN L. (2001). Fonctionnement écologique de la Seine à l’aval de la station d’épuration d’Achères : données expérimentales et modélisation bidimensionnelle. Thèse de doctorat, École des Mines de Paris, Paris, France, 279 p.
- POULIN M. (2006). Réalisation de simulations PROSE, Année de référence 2003. École des Mines de Paris pour le Syndicat Interdépartemental d’Assainissement de l’Agglomération Parisienne, rapport no R060629, 83 p.
- INERIS (2005). Circulaire DCE n°2005-12 : http:// www.ineris.fr/aida/?q=consult_doc/consultation/2.250.190.28.8.2901 (consultation en avril 2009).
- Service d’Administration Nationale des Données et Référentiels sur l’Eau (Sandre).Directive Cadre Eau : http://sandre.eaufrance.fr/rubrique.php3?id_rubrique=21 (consultation en janvier 2008).
- Ifremer.http://www.ifremer.fr/delcc/cycleau/reglementation/seqeau.htm (consultation en juillet 2009).
List of figures
Figure 1
Réseau modélisé par ProSe et localisation des 27 stations du RNB.
Hydrographic network modeled by ProSe and location of 27 RNB measurement sites.
Figure 2
Comparaison des chroniques fournies par ProSe et mesurées par le RNB pour les différents indicateurs. Exemple de la station 10.
Comparison of simulated (ProSe) and measured (RNB) time series for all considered indicators. Example of measurement site 10.
Figure 3
Comparaison de la variabilité à petit pas de temps des différents indicateurs simulés par ProSe et mesurés par le RNB. Variogrammes temporels simples et croisés des valeurs instantanées, calculés à pas hebdomadaire, à Suresnes.
Comparison of spatial variability for short time steps of simulated (ProSe) and measured indicators at a given location (Suresnes).
Figure 4
P rincipe de calcul du quantile 90 selon la " méthode améliorée ". a) Définition des segments d'influence àpartir des mesures. b) Pondération et linéarisation du quantile empirique; Z(i) désigne la valeur de rang i, aprèsclassement des mesures Zj par ordre croissant.
Principle of the 90-percentile calculation by the "improved method". a) Definition of influence segments frommeasurements. b) Weighting and linearizing the empirical quantile; Z(i) denotes the value of rank i after orderingthe measurements Zj by increasing order.
Figure 5
L es différentes méthodes de spatialisation des quantiles 90 pour obtenir les pourcentages d'occurrence dans chaque classe de qualité.
Different methods to spatialize the 90-percentiles in order to attribute occurrence percentages to each quality class.
Figure 6
M éthodes de calcul du quantile 90 et de spatialisation de cequantile.
Methods to calculate 90-percentile and to spatialize it.
Figure 7
Caractérisation de l'état des eaux selon le SEQ-Eau pour les nitrates; les pourcentages 'occurrence des quantiles 90 temporels dans chaque classe de qualité sont indiqués par MECE, élimitées suivant les pk (km).
Characterization of water quality according to SEQ-Eau system for nitrates; occurrence ercentages of 90-percentiles in each quality class are given for each "Stream Water Body", defined according to the pk (km).
Figure 8
Caractérisation de l'état des eaux selon le SEQ-Eau pour : (a) l'ammonium, et (b) l'oxygène dissous; les pourcentages d'occurrence des quantiles 90 temporels dans chaque classe de qualité sont indiqués par MECE, délimitées suivant les pk (km).
Characterization of water quality according to SEQ-Eau system for (a) ammonium and (b) dissolved oxygen; occurrence percentages of 90-percentiles in each quality class are given for each "Stream Water Body", defined according to the pk (km).
Figure 9
Caractérisation de l'état des eaux selon le SEQ-Eau pour : (1) les matières en suspension, et (b) les orthophosphates; les pourcentages d'occurrence des quantiles 90 temporels dans chaque classe de qualité sont indiqués par MECE, délimitées suivant les pk (km).
Characterization of water quality according to SEQ-Eau system for (a) suspended matter and (b) orthophosphates; occurrence percentages of 90-percentiles in each quality class are given for each "Stream Water Body", defined according to the pk (km).
List of tables
Tableau 1
É carts relatifs (E.rel.), différences relatives (D.rel.) et écarts quadratiques absolus (E².abs.) moyens entre quantiles 90 calculés et quantiles de référence
Table 1. Average relative deviations (E. rel), relative differences (D. rel) and absolute squared deviations (E². abs.) between calculated and reference 90-percentiles.
Tableau 2
Écarts E, différences D, et écarts quadratiques E2 moyens entre quantiles 90 calculés et quantiles de référence en conservant une station du RNB sur deux.
Table 2. Average relative deviations (E. rel), relative differences (D. rel) and absolute squared deviations (E². abs.) between calculated and reference 90-percentiles when considering half of the measurement sites.