Abstracts
Abstract
In this study, three models for the simulation of the number of breaks in a water main network are presented and compared: linear regression, the Weibull-Exponential-Exponential (WEE), and the Weibull-Exponential-Exponential-Exponential (WEEE) models. These models were calibrated using a database of recorded breaks in a real water main network of a municipality in the province of Québec, for the observation period 1976 to 1996, with the least squares and the maximum likelihood methods. The ability of these models to predict breaks over time was then evaluated by comparing the predicted number of breaks for the years 1997 to 2007 with the observed breaks in the network over the same time period. Results show that if the period of observation is short (around 20 years), calibration of the WEE and WEEE models with the maximum likelihood method leads to estimates that are closer to the observations than when these models are calibrated with the least squares method. When the observation period is longer (around 30 years), the predictions obtained with the models calibrated using the maximum likelihood or the least squares methods are similar. However, the use of the maximum likelihood method for calibration is only possible when data for the occurrence of each break for each pipe of the network are available (a pipe being a homogeneous network segment between two adjacent street junctions). If this is not the case, a trend line will be sufficient to predict the number of breaks over time, though this type of curve does not allow to account for pipe replacement scenarios. If the only information available is the total number of breaks on the network each year, then the impact of replacement scenarios could be simulated with the WEE and WEEE models calibrated using the least squares method.
Key Words:
- Exponential distribution,
- least squares,
- maximum likelihood,
- water network analysis,
- probabilistic model,
- Weibull distribution
Résumé
Trois modèles pour la simulation du nombre de bris sur un réseau d’aqueduc sont présentés et comparés, soit un modèle de régression linéaire et deux autres modèles statistiques que sont les modèles Weibull-Exponentiel-Exponentiel (WEE) et Weibull-Exponentiel-Exponentiel-Exponentiel (WEEE). Ces modèles étaient calés avec deux méthodes distinctes, soit les méthodes des moindres carrés et du maximum de vraisemblance, en utilisant une base de données des bris enregistrés sur un réseau d’aqueduc réel d’une municipalité du Québec, pour la période de 1976 à 1996. La capacité de ces modèles à prédire les bris dans le temps a ensuite été évaluée en comparant les bris prédits pour les années 1997 à 2007 avec les bris observés sur le réseau au cours de la même période. Les résultats montrent que lorsque la période d’observation des bris est courte (de l’ordre de 20 ans), le calage des modèles WEE et WEEE à l’aide de la méthode du maximum de vraisemblance conduit à des estimations qui s’approchent plus des observations que lorsque ces modèles sont calés avec la méthode des moindres carrés. Lorsque la période d’observation est plus longue (environ 30 ans), les prédictions issues des modèles calés selon ces deux méthodes de calage sont pratiquement similaires. L’application de la méthode du maximum de vraisemblance n’est cependant possible que si la date d’occurrence des bris est connue pour chacune des conduites du réseau (une conduite étant un tronçon homogène du réseau qui s’étend d’un coin de rues à un autre). Si ce n’est pas le cas, une courbe de régression linéaire permet de bien estimer l’évolution du nombre de bris annuel à court terme. Par contre, la régression linéaire ne permet pas de tenir compte du remplacement éventuel de conduites. Si la seule information disponible pour caler les modèles est le nombre total de bris sur le réseau chaque année, l’impact de scénarios de remplacement peut être simulé avec les modèles WEE et WEEE calés selon la méthode des moindres carrés.
Mots-clés:
- Analyse de réseau de distribution d'eau,
- distribution exponentielle,
- distribution de Weibull,
- maximum de vraisemblance,
- modèle probabiliste,
- moindres carrés
Article body
1. Introduction
The structure of aging pipes becomes increasingly fragile largely due to corrosion of their inner surfaces or linings (SCHOCK, 1990) and poses major financial challenges for municipalities and concerns regarding the quality of services for citizens. Subject to the various forces acting on them, weakened pipes are susceptible to breaks (EISENBEIS, 1994). This, in turn, can cause a leak, which once detected, can be repaired. Despite a certain number of interventions (repairs and replacements of pipes), pipe breaks continue to increase in several North American cities (DUCHESNE et al., 2011). The history of these interventions, if recorded, provides a good indication of the structural state and aging of the pipe network. In recent years, certain water network managers have recorded these interventions, thus creating an historical database of pipe breakages. In order to better plan their investments, municipalities should be equipped with tools enabling them to track and predict the evolution of pipe aging (DUCKSTEIN and PARENT, 1994; GERMANOPOULOS et al., 1986).
Two significant reviews of the different models used to evaluate the structural deterioration of pipes were conducted in KLEINER and RAJANI (2001) and RAJANI and KLEINER (2001). The authors classified these models into two categories: deterministic and probabilistic. Furthermore, they underlined the difficulty in gathering the amount of data required to establish a deterministic model capable of simulating the aging of pipes throughout an entire pipe network (KLEINER and RAJANI, 2001). WALSKI and PELICCIA (1982) also underlined the difficulty in gathering the amount of data required to establish a deterministic model capable of simulating the aging of pipes throughout an entire distribution system. Additionally, BERARDI et al. (2008) argued that efforts to introduce complex analytical techniques become futile when data are either not available or are of poor quality. Hence, to model the aging of pipes in water distribution networks, probabilistic models should be used, except in the case where sufficient data are available to use a deterministic approach for predicting asset failure.
Comprehensive reviews of the literature concerning probabilistic models predicting the rate of water main pipe breaks can be found in VILLENEUVE et al. (1998), PELLETIER (2000), MAILHOT et al. (2000), GOULTER and KAZEMI (1988 and 1989), TSITSIFLI and KANAKOUDIS (2010), TSITSIFLI et al. (2011) and JOWITT and XU (1993). VILLENEUVE et al. (1998), used survival analysis to model the time elapsed between successive breaks. To use survival analysis in a classical manner (calibration by the maximum likelihood) however, one must know the complete history of the breakages, the time elapsed between pipe installation and the first break, the time between the first and second break, and so forth. In addition, studies have shown that the time between two successive breaks is different from the amount of time between installation and the first break (CLARK and GOODRICH, 1989; CLARK et al., 1982; ANDREOU et al., 1987). Thus, a different statistical distribution should be used to represent each of these intervals. The most frequently used statistical distributions to represent the time between pipe installation and the first pipe break or the time between two successive breaks are the Weibull and exponential distributions (ANDREOU et al., 1987; EINSENBEIS, 1994). PELLETIER (2000) and MAILHOT et al. (2000) developed a statistical modeling approach that takes into consideration the periods when pipe failures were and were not recorded. This was the first appearance of this methodological approach in the literature to model water main pipe breaks. Case studies were conducted demonstrating the pertinence and validity of this methodology (PELLETIER, 2000; PELLETIER et al., 2003). This approach was also used to establish an optimal process to replace pipes (MAILHOT et al., 2003). KANAKOUDIS and TOLIKAS (2001) also introduced a methodology that calculated the optimum replacement time for the pipes of a water network. This was done by performing a techno-economic analysis that took into account the costs related to the repair or replacement of trouble-causing parts of a network. GOULTER et al. (1993), JOWITT and XU (1993), KANAKOUDIS (2004), and KANAKOUDIS and TOLIKAS (2004) also provide examples of methodologies for optimal replacement.
TOUMBOU et al. (2014), inspired by the approach of MAILHOT et al. (2000), developed a general model which permits the use of explanatory covariates which take into account factors which can lead to pipe breaks (pipe age, pressure, temperature, soil humidity, pipe diameter and length, type of pipe material, etc.). The study by TOUMBOU et al. (2014) was primarily focused on the theoretical development of the general model, which advantageously allows for combinations of distributions permitting better predictions of pipe breaks over time. If the last distribution used in the combination is exponential, one can calculate analytically the average annual number of failures in a network since an equation can be developed to estimate the probability of failure of each of the pipes during a given year. Several other models using explanatory covariates have been developed (LE GAT and EISENBEIS, 2000; KLEINER and RAJANI, 2001; RAJANI and KLEINER, 2001; KRETZMANN and VAN ZYL, 2004; VANRENTERGHEM-RAVEN, 2008; DAVIS et al., 2008; BERARDI et al., 2008; YAMIJALA et al., 2009; WANG et al., 2009; KLEINER et al., 2009; ALVISI and FRANCHINI, 2010).
In the present study, we propose and compare three models for the simulation of pipe breaks in a water main network: a linear regression model, the Weibull-Exponential-Exponential (WEE) model and the Weibull-Exponential-Exponential-Exponential (WEEE) model, each of which are described in detail. The objectives were to evaluate the capability of the three models to predict future pipe breaks, to identify the best suited model as a function of the modeling objectives and to determine the most appropriate calibration method for the WEE and WEEE models, according to the available data. All these evaluations were performed using a database of recorded breaks in a real water main network of a municipality in the province of Quebec.
2. Case Study
The database of the municipality under study includes breaks that were observed and recorded from 1976 to 2007, on the pipes of its water distribution network that were in place in 2008. In addition to the number of breaks on each pipe by year, the database contains the pipe installation dates (from 1944 to 2006) and the diameter and length of each pipe. The network, in 2008, contained 10 258 pipe segments for a total pipe length of 396 km. Pipe segments, that we refer to simply as “pipes” throughout the text, are defined as portions of the water distribution network that are located between two adjacent street junctions, with constant slope, diameter, and material. The discretization of the network into pipes was carried out by the City’s staff. The database used for model development and calibration was constructed by the authors, from data provided by the City. For the breaks that occurred from 1997 to 2007, the City provided two geo-referenced databases: one for the pipes and one for the breaks. The spatial joint of these two databases was performed by the authors. For the breaks that occurred from 1976 to 1996, the City provided, along with a geo-referenced database of the network, a list of the break dates with the civic address of the nearest building. Many operations were conducted by the authors to locate these breaks on the corresponding pipes, including spatial joints, corrections of street names and manual localizations. The numerical operations involved in the construction of the final database were performed rigorously, in an attempt to include as much information as possible and to make sure this information reflected what was provided by the City. However, it is possible that not all of the pipe breaks in the water network, from 1976 to 2007, were recorded properly by the City. In the absence of other information, we can only assume that the provided databases accurately represented the state of the pipe network. Furthermore, the increasing trend in the annual total pipe breaks and their interannual variability suggest that the breaks were properly recorded.
3. Presentation of the Models
In this study, only time (t) was used as an explanatory variable to model the evolution of breaks in the system. As presented in TOUMBOU et al. (2014), other explanatory variables (e.g. pipe diameter or material) can be integrated in the models. However, it was observed that the presence or absence of the pipe diameter and material in the model did not significantly change the results when computing the total annual number of breaks for the whole network (when the models integrating explanatory variables were simulated and compared to those without explanatory variables for several networks in the province of Quebec; see DUCHESNE et al., 2011). Indeed, the incorporation of explanatory variables other than time into the model can significantly affect the probability that a specific pipe will break during a specific year, but the total number of breaks for the entire network during a year might not be affected. For this reason the only explanatory variable considered in this paper is time (t). Three models are used and compared in this paper. Each of them is described briefly below.
If the sole objective of a municipality is to evaluate the evolution of pipe breaks over time the simplest method is to fit a linear regression. However, the use of a linear regression does not allow to take into account different explanatory factors or pipe replacement scenarios. In this case, the model which is used is a linear regression of the form:
where y represents the annual number of pipe breaks, x is the number of years since the reference year, and a and b are parameters which value is determined during calibration.
To better reflect the evolution of pipe breaks over time as well as to account for pipe replacements, models that take these aspects into account should be used. Water distribution pipe breaks can be likened to a failure rate process that is represented by survival functions as amply shown in the literature (VILLENEUVE et al., 1998; PELLETIER, 2000; MAILHOT et al., 2000; MAILHOT et al., 2003; KLEINER and RAJANI, 2001; RAJANI and KLEINER, 2001; KRETZMANN and VANZYL, 2004; VANRENTERGHEM-RAVEN, 2008; BERARDI et al., 2008; DAVIS et al., 2008; KLEINER et al., 2009; WANG et al., 2009; YAMIJALA et al., 2009; TOUMBOU et al., 2014). Here, we use the exponential and Weibull distributions (KALBFLEISCH and PRENTICE, 2003) to build the two models under study: WEE and WEEE. The corresponding survival functions, that represent the distribution of the time elapsed between two successive breakages or between the first break and pipe installation, are written respectively:
where FE is the exponential survival function, FW is the Weibull survival function, t represents time, and k and p are scalar parameters.
The WEE model represents the time elapsed from installation to the first break using a Weibull distribution, the time elapsed between the first and second break using an exponential distribution, and the time between subsequent breaks using another exponential distribution. A similar definition holds for the WEEE model.
4. Calibration of the Models
For the linear model, the value of the parameters a and b were obtained by using the least squares (LS) method consisting of minimizing the sum of squared deviations between the annual numbers of observed and simulated breaks in the network for each year of the calibration period. For the other models, calibration was more complex, as we explain in the section which follows.
Two methods are considered for the calibration of the WEE and WEEE models, namely the least square (LS) and the maximum likelihood (ML) methods. To apply the LS method, it is required to compute the total number of pipe breaks for each year. To apply the ML method, the likelihood function must be developed. These two developments are detailed in the following sections.
4.1 Calculation of the average annual number of breakages
The average number of breakages for a pipe between T and T + DT can be found using:
with P(a, b) the probability of having a breaks between 0 and T, and b breaks between T and T + DT.
The general equation to estimate the average number of breakages, given in Equation 3, was developed in TOUMBOU et al. (2014) for the WEE model and the following equation was obtained:
with
and
where k2 and k3 are calibration parameters.
An equation to calculate the average number of breaks can also be obtained for the WEEE model using the general model presented in TOUMBOU et al. (2014) as follows:
with
and
where k4 is a calibration parameter.
Thus, the cumulative number of breaks in the whole network (N pipes), for a given year A, can be calculated using the following equation:
In this paper, the cumulative number of breaks given in Equation 6 was used for model calibration with the LS method and also for the simulation of the total annual number of breakages.
4.2 Calculation of the likelihood function
To establish the likelihood function for the WEE and WEEE models, one must first calculate P(n), n ≥ 0, which is the probability of having n breakages between Tb and Ta regardless of the number of breaks between 0 and Tb. The likelihood function is written as follows:
where par is the vector of parameters ((kj, pj) where j = 1, 2, …m + n), bi is the number of recorded breaks for pipe i, N is the total number of pipes in the network and Pi(bi) is the probability for pipe i to have bi breaks between Tb and Ta, the starting and ending time of data collection period, regardless of the number of breaks between 0 and Tb.
To determine the value of the model parameters for WEE, the following function, namely the natural logarithm of the likelihood function, was maximized:
where
For the WEEE model, the logarithmic expression of the likelihood function L is shown in equations 10 and 11.
5. Results
In order to simulate the evolution of the annual number of breakages in the network, the parameter values in each of the models were first evaluated. Since we sought to verify the capability of the models to predict future breaks, the models were first calibrated using the period from 1976 to 1996. This then allowed comparing the model-based predictions with the actual observations which were recorded from 1997 to 2007.
To demonstrate the ability of simulating replacement scenarios, the WEEE model, as an example, was calibrated using the data from 1976 to 2007. The annual number of breaks simulated with this model from 1997 to 2007 was then compared to the number of breaks simulated with the WEEE model calibrated using the data from 1976 to 1996, and assuming a pipe annual replacement rate equal to 0.5% of the total network length (which is the average annual replacement rate that the municipality actually applied from 1997 to 2007, that can vary between pipe material and diameter). Finally, the WEEE model was used to simulate the impact on the annual number of breaks of four pipe replacement scenarios: 0.5%, 1.0%, 1.5%, and 2.0% replacement of the total network length.
where
5.1 Calibration for the period 1976 to 1996
Calibration of the WEE and WEEE models was carried out using the LS and ML methods while considering the state of the network in 1996. Values of the parameters for this calibration are presented in Table 1. Note that this calibration was carried out under constraints to meet the assumption that successive breaks occur more and more frequently (k1 < k2 < k3 < …< kn). The calibration of the linear model was conducted using the LS method. The obtained parameters were: a = 4.2416 and b = -231.99.
Table 1
Calibration parameter values for the period 1976 to 1996
Valeur des paramètres de calage pour la période 1976 à 1996
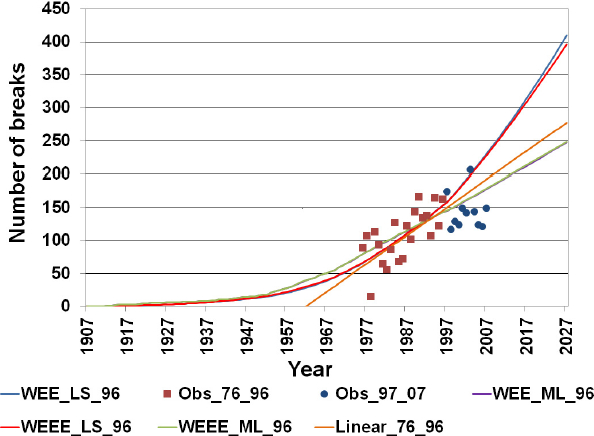
Then these parameters were used to simulate the average number of annual breaks. Simulated break curves are presented in Figure 1. In this figure, one can see that the calibration by the LS method overestimates the predicted number of breaks compared to the observed breaks from 1997 to 2007. It is also evident that the ML method seems the most realistic in terms of prediction of pipe breaks. This shortcoming of the LS method is likely linked to the small amount of available data to determine the values of the parameters as demonstrated by BAYRAK and AKKAYA (2010) and TSURU and HIROSE (2009). In fact, for the LS method, there were only 21 data points, representing the annual number of breaks for the period from 1976 to 1996. In contrast, using the ML method, we were able to incorporate information for each of the 9 233 pipes that were in the network in 1996. This included each break, its date of occurrence, the age of the pipe at the time of breakage, and the age of the remaining unbroken pipes. This leads us to conclude that if one has all of the information for each of the pipes, then it is more appropriate to use the ML method for short observation periods. If all of the necessary information to apply this method is not available, then a simple trend line can provide satisfactory results as seen in Figure 1.
Figure 1
Results of the calibrated models for the observation period from 1976 to 1996 and observed breaks (the WEE_ML_96 and WEEE_ML_96 curves overlap). LS: least squares; ML: maximum likelihood; 96: calibrations on the 1976-1996 period
Résultats des modèles calés avec les observations de la période 1976 à 1996 et nombre annuel de bris observés (les courbes WEE_ML_96 et WEEE_ML_96 sont superposées)
Figure 1 also shows that the results of the simulations for the two models WEE and WEEE are very similar for each of the two calibration methods, as their respective curves are overlapping. For the remainder of the study we thus employed the WEEE model. Although the number of simulated pipe failures by both the WEE and WEEE models were similar, the WEEE model seems best suited for the case study. Indeed, as shown in Table 2, the number of third or more breaks is relatively important at 4.07% of pipes in the studied network, and the WEEE model uses different distributions for the first, second, third, fourth, and subsequent breaks, while only three distributions are used in the WEE model (for the first, second, third, and subsequent breaks).
Table 2
Percentage of pipes according to the total recorded number of breaks
Pourcentage de conduites selon le nombre total de bris enregistrés
5.2 Calibration for the period 1976 to 2007
The WEEE model was calibrated with the observed data for the period from 1976 to 2007, using the LS and ML methods. The calibration values are presented in Table 3. Once again, this calibration was carried out under the assumption that successive breaks occur more and more frequently.
Table 3
Calibration parameter values for the period 1976 to 2007
Valeurs des paramètres de calage pour la période 1976 à 2007
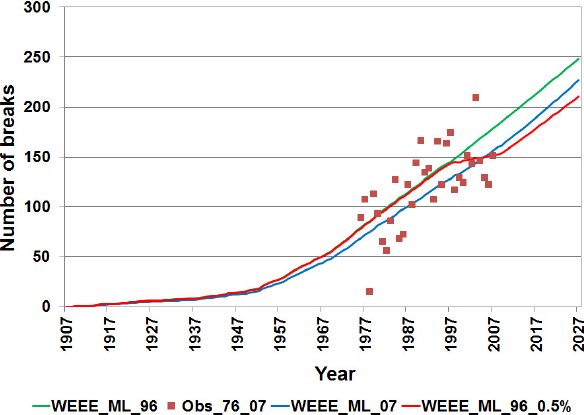
Considering the observations from 1976 to 2007, consisting of 32 data points representing the average annual number of breaks and 10 258 pipes in the network in 2008, the number of failures simulated by the LS method was very similar to that simulated by the ML method (Figure 2). This can be explained by the fact that there are more observed data than in the previous assessments, allowing for a better calibration with the LS method. It should be noted that here, the ML method used information from 10 258 pipes in the network in 2008, while the LS method only required 32 observations to generate similar results.
Figure 2
Results of the calibrated models for the observation period from 1976 to 2007 and observed breaks. LS: least squares; ML: maximum likelihood
Résultats des modèles calés avec les observations de la période 1976 à 2007 et nombre annuel de bris observés
The linear regression, with parameter values a = 2.7945 and b = -118.65, also gave very good results. It is important to note that the linear regression model allows for the simulation of the evolution of pipe breaks, as shown in figures 1 and 2, however, it does not take into account certain factors such as the diameter, length, or type of material of the pipes. Additionally, this model does not allow pipe replacement scenarios to be taken into consideration when simulating the annual number of pipe breaks. As a result, to account for these important factors, it is necessary to resort to other statistical models such as the WEE and WEEE models.
5.3 Capability of the models to predict future pipe breaks
To validate the predicted values generated by the models, it was necessary to compare them with the recorded observations. However, the values simulated with the models are averages of the annual numbers of pipe breaks. Given the dispersion in the observed values, it was difficult to directly compare them with those provided by the models. In order to make this comparison, we determined the observed average annual values from the cumulative break curve. In order to do this, a second degree polynomial was fit to the cumulative observed break curve. For all practical purposes these curves are overlapping (Figure 3). We then differentiated the resulting cumulative model, which gives what we have designated as the average observed annual breaks (AOAB). The line representing these average values is slightly above the trend line and the curve simulated by the WEEE_ML_07 model which were previously obtained (Figure 4).
Figure 3
Cumulative breaks from 1976 to 2007, observed and simulated with a second degree polynomial
Bris cumulés de 1976 à 2007, observés et simulés avec un polynôme du second ordre
Figure 4
Results for the derived model (AOAB), the WEEE_ML_07 model and the linear regression, compared to the observations from 1976 to 2007. ML: maximum likelihood
Résultats du modèle dérivé (AOAB), du modèle WEEE_ML_07 et de la régression linéaire, comparés avec les observations pour la période de 1976 à 2007
Thus, we used this average to evaluate the predictive abilities of the WEE and WEEE models. In Table 4, we present the pipe breaks for different years, for the period 1997 to 2007, which were predicted by the WEEE_ML_96, WEEE_LS_96, and AOAB models.
Table 4
Predicted number of average annual breakages with the WEEE and AOAB models
Nombre annuel moyen de bris prédits avec les modèles EEE et AOAB
As compared to the AOAB model, the best predictive model to use, assuming the network was in the same state as it was in 1996, is the WEEE calibrated with the ML method. The maximum annual difference between the results for both models (3.5%) was reached in 2007 (173 breaks for the AOAB model and 179 breaks for the WEEE_ML_96 model), which was an excellent result given both the short observation period and the dispersion of the observed breaks (Table 4).
During the period from 1997 to 2007, the city carried out an average pipe replacement rate of 0.5% of the total network length per year. To validate the model, the simulated results of the WEEE_ML_96 model (calibrated with data from 1976 to 1996) assuming a pipe replacement scenario of 0.5% over the period 1997 to 2007, were thus compared to those obtained from the WEEE_ML_07 model (calibrated with data from 1976 to 2007). Results of these simulations are presented in Table 5.
Table 5
Predicted number of average annual breakages with the WEEE model for different scenarios
Nombre annuel moyen de bris prédits avec le modèle WEEE pour différents scénarios
Results obtained from the WEEE_ML_96 model with a 0.5% replacement scenario and WEEE_ML_07 model were similar from 2003 onward. Figure 5 illustrates the data which are presented in Table 5 and, again, shows the ability of the model to simulate the evolution of pipe breaks and the ability to model pipe replacement scenarios.
Figure 5
Simulation of the 0.5% pipe replacement scenario on the 1996 network and comparison with the WEEE_ML_96 model results, the WEEE_ ML_07 model results, and the observed breaks. ML: maximum likelihood
Simulation du scénario annuel de remplacement de 0,5 % de la longueur totale du réseau de 1996 et comparaison avec les résultats du modèle WEEE_ML_96, les résultats du modèle WEEE_ML_07 et les bris observés
5.4 Implementation of replacement scenarios
As previously stated, the importance of the WEE and WEEE models is their ability, when calibrated, to simulate replacement scenarios in a water main network. These scenarios indicate what will happen to the evolution of annual breaks after replacement of pipes in the network. This information is essential for municipalities which would like to both plan pipe replacements and know what effect they will have on the number of annual breaks. Independent of social costs, municipalities can evaluate the costs of each scenario and compare them with the costs of damage repair. Furthermore, they can establish maintenance and repair policies knowing the short and long term impacts of their efforts. However, although models simulating the evolution of the number of pipe breaks over time are quite helpful in assessing the global costs associated with the renewal of water pipes, the actual decision to replace a pipe is often based on a variety of other factors, including inspection data, hydraulic performance and required work on other pipes located in the same trench. In the following, we assume that the oldest pipes take priority for replacement.
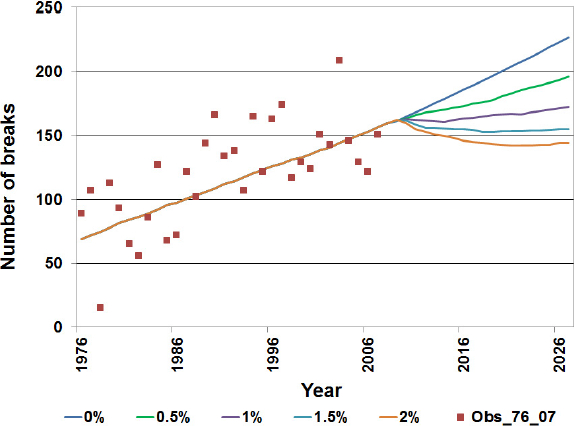
The WEEE_ML_07 was used to simulate four pipe replacement scenarios. The average annual replacement rates of 0.5%, 1.0%, 1.5%, and 2.0% of the total network length were used as example scenarios. The results of these simulations are presented in Figure 6 and Table 6. These results demonstrate that, in order to maintain the same average annual rate of pipe breakage as in 2009 (162 breaks), it is necessary to replace 1.5% of the length of the network annually. If the municipality under study maintains an average rate of 0.5% replacement, as was done over the course of the last ten years, the average annual number of breakage will increase from 162 in 2009 to 196 in 2027.
Figure 6
Replacement scenarios simulated with the WEEE_ML_07 model
Scénarios de remplacement simulés avec le modèle WEEE_ML_07
Table 6
Predicted annual number of breaks according to various pipe replacement scenarios (the indicated percentages correspond to the percentage of total length of the network)
Nombre annuel de bris simulés selon différents scénarios de remplacement de conduites (les pourcentages indiqués correspondent à des pourcentages de la longueur totale du réseau)
6. Conclusion
Calibrations and simulations with the WEE and WEEE models in this study were made possible by the models generalized by TOUMBOU et al. (2014). We first demonstrated the ability of the aforementioned models to predict annual pipe breaks over time. We also evaluated the capacity of these models to incorporate specific pipe replacement scenarios in a water main network. This was achieved by using replacement and break data provided by the municipality under study. If the period of observation is short (less than 25 observations), we recommend using the ML method for calibration, however this is only possible when one has access to all of the information for each of the pipes of the network. If this is not the case, a trend line will be sufficient to predict the number of breaks over time, if no changes are made to the network; though this type of curve does not allow one to account for pipe replacement scenarios. If information for each of the pipes is not available and replacement scenarios need to be accounted for, then the models could be calibrated with the LS method. These results were obtained using only pipe age as an explanatory variable to model the occurrence of pipe breaks. Using covariates such as pipe diameter, length, or material could be possible with the WEE and WEEE models but would most probably lead to the same conclusions.
Appendices
Appendix
Notations
bi |
number of breakages between Tb and Ta |
DT |
elapsed time after T |
FE |
exponential survival function |
fi |
probability density function of break i |
Fi |
survival function of break i |
fw |
Weibull probability density function |
FW |
Weibull survival function |
k |
scalar calibration parameter |
kj |
parameter of the distribution corresponding to the jth break |
L |
likelihood function |
m |
maximum number of pipe breaks occuring between T0 = 0 and T |
n |
maximum number of pipe breaks occuring between T and T + DT |
N |
total number of pipes in the network |
p |
scalar calibration parameter |
pj |
parameter of the distribution corresponding to the jth break |
P(i, j) |
probability of having i breakages between T0 = 0 and T and j breakages between T and T + DT |
P(k) |
probability of having n breakages for a pipe between T and T + DT, regardless of the number of breakages between 0 and T |
t |
time |
ti |
timing of the ith break that occurs before T |
tj |
timing of the jth break that occurs before T |
T |
given time after pipe installation |
T0 |
time of a pipe’s installation |
Ta |
end of data collection period |
Tb |
start of data collection period |
μ(a, b) |
probability of having n breakages of a pipe between a and b, regardless of the number of breakages between 0 and a |
Acknowledgments
This research was funded by the Canadian and Quebec governments via the Municipal Rural Infrastructure Fund, by the City of Québec and by the Natural Sciences and Engineering Research Council of Canada. The authors greatly acknowledge the support of these organizations. The authors also thank the municipality who provided the data used in this study, not named here for reasons of confidentiality.
References
- ALVISI S. and M. FRANCHINI (2010). Comparative analysis of two probabilistic pipe breakage models applied to a real water distribution system. Civ. Eng. Environ. Syst., 27(1), 1-22.
- ANDREOU S.A., D.H. MARKS and R.M. CLARK (1987). A new methodology for modelling break failure patterns in deteriorating water distribution systems: Theory. Adv. Water Resour., 10(1), 2-10.
- BAYRAK O.T. and A.D. AKKAYA (2010). Estimating parameters of a multiple autoregressive model by the modified maximum likelihood method. J. Comput. Appl. Math., 233(8), 1763-1772.
- BERARDI L., O. GIUSTOLISI, Z. KAPELAN and D.A. SAVIC (2008). Development of pipe deterioration models for water distribution systems using EPR. J. Hydroinform., 10(2), 113-126.
- CLARK R.M. and J.A. GOODRICH (1989). Developing a data base on infrastructure needs. JAWWA, 81(7), 81-87.
- CLARK R.M., C.L. STAFFORD and J.A. GOODRICH (1982). Water distribution systems: a spatial and cost evaluation. J. Water Resour. Plann. Manage. - ASCE, 108(WR3), 243-256.
- DAVIS P., D.D. SILVA, D. MARLOW, M. MOGLIA, S. GOULD and S. BURN (2008). Failure prediction and optimal scheduling of replacements in asbestos cement water pipes. J. Water Supply: Res. T. - AQUA, 57(4), 239-252.
- DUCHESNE S., J.-P. VILLENEUVE, B. TOUMBOU, N. BOUZIDA, G. BEARDSELL, M. K. FORTIN and A. LUCCHESI LAVOIE (2011). Modélisation des bris d’aqueduc et analyse des résultats pour la Ville de Québec. Report No 1290, Institut national de la recherche scientifique – Centre Eau Terre Environnement, Québec, Canada.
- DUCKSTEIN L. and E. PARENT (1994). Systems engineering of natural resources under changing physical conditions: a framework for reliability and risk. In: Engineering Risk in Natural Resources Management, L. Duckstein and E. Parent (eds), Kluwer Academic Publishers, The Netherlands, pp. 5-19.
- EISENBEIS P. (1994). Modélisation statistique de la prévision des défaillances sur les conduites d'eau potable. Ph.D. Thesis, Université Louis Pasteur, Strasbourg, France, 154 p.
- GERMANOPOULOS G., P. JOWITT and J. LUMBERS (1986). Assessing the reliability of supply for water distribution systems. P. I. Civil Eng., 80(Apr. part I), 413-428.
- GOULTER I. and A. KAZEMI (1988). Spatial and temporal groupings of water main pipe breakage in Winnipeg. Can. J. of Civ. Eng., 15(1), 91-97.
- GOULTER I. and A. KAZEMI (1989). Analysis of water distribution pipe failure types in Winnipeg, Canada. J. Transp. Eng. - ASCE, 115(2), 95-111.
- GOULTER I., J. DAVIDSON and P. JACOBS (1993). Predicting water-main breakage rates. J. Water Resour. Plann. Manage. - ASCE, 119(4), 419-436.
- JOWITT P.W. and C. XU (1993). Predicting pipe failure effects in water distribution networks. J. Water Resour. Plann. Manage. - ASCE, 119(1), 18-31.
- KALBFLEISCH J.D. and R.L. PRENTICE (2003). The Statistical Analysis of Failure Time Data. Wiley/Interscience, New-York, NY, USA, 462 p.
- KANAKOUDIS V. (2004). Vulnerability based management of water resources systems. J. Hydroinform., 6(2), 133-156.
- KANAKOUDIS V. and D. TOLIKAS (2004). Assessing the performance level of a water system. Water Air Soil Pollut. Focus, 4(4-5), 307-318.
- KLEINER Y. and B. RAJANI (2001). Comprehensive review of structural deterioration of water mains: statistical models. Urban Water, 3(3), 131-150.
- KLEINER Y., A. NAFI and B. RAJANI (2009). Planning renewal of water mains while considering deterioration, economies of scale and adjacent infrastructure. In: Proceedings of the 2nd International Conference on Water Economics, Statistics and Finance, IWA Specialist Group Statistics and Economics, Alexandroupolis, Greece, July 3, pp. 1-13.
- KRETZMANN H. and J. VAN ZYL (2004). Stochastic analysis of water distribution systems. In: Proceedings of the 2004 World Water and Environmental Resources Congress: Critical Transitions in Water and Environmental Resources Management, June 27 - July 1, Salt Lake City, UT, American Society of Mechanical Engineers, pp.4623-4632.
- LE GAT Y. and P. EISENBEIS (2000). Using maintenance records to forecast failures in water networks. Urban Water, 2(3), 173-181.
- MAILHOT A., G. PELLETIER, J.-F. NOEL and J.-P. VILLENEUVE (2000). Modeling the evolution of the structural state of water pipe networks with brief recorded pipe break histories: Methodology and application. Water Resour. Res., 36(10), 3053-3062.
- MAILHOT A., A. POULIN and J.-P. VILLENEUVE (2003). Optimal replacement of water pipes. Water Resour. Res., 39(5), 1-14.
- PELLETIER G. (2000). Impact du remplacement des conduites d’aqueduc sur le nombre annuel de bris. Ph.D. Thesis, Institut national de la recherche scientifique, Sainte Foy, Québec, Canada, 240 p.
- PELLETIER G., A. MAILHOT and J.-P. VILLENEUVE (2003). Modeling water pipe breaks - Three case studies. J. Water Resour Plann. Manage., 129(2), 115-123.
- RAJANI B. and Y. KLEINER (2001). Comprehensive review of structural deterioration of water mains: Physically based models. Urban Water, 3(3), 151-164.
- SCHOCK M.R. (1990). Internal corrosion and deposition control. In: AWWA Water Quality and Treatment: A Handbook of Community Water Supplies. F.W. PONTIUS (Ed.), McGraw Hill, New-York, NY, USA, pp. 997-1111.
- TOUMBOU B., J.-P. VILLENEUVE, G. BEARDSELL and S. DUCHESNE (2014). A general model for water distribution pipe breaks: Development, methodology and application to a small city in Quebec, Canada. J. Pipeline Syst. Eng. Pract. DOI:10.1061/(ASCE)PS.1949-1204.0000135.
- TSITSIFLI S. and V. KANAKOUDIS (2010). Predicting the behavior of a network pipe using the "critical z-score" as its performance indicator. Desalination, 250(1), 258-265.
- TSITSIFLI S., V. KANAKOUDIS and I. BAKOUROS (2011). Pipe networks risk assessment based on survival analysis. Water Resour. Manage., 25(14), 3729-3746.
- TSURU K., and H. HIROSE (2009). Estimation for the parameters in the step-up voltage test under the Weibull power law model. Engineering Letters, 17(2), EL_17_2_10.
- VANRENTERGHEM-RAVEN, A. (2008). Water pipes asset management: Evaluation of EU CARE-W. In: Proceedings of the 8th Annual Water Distribution Systems Analysis Symposium, pp. 1-13.
- VILLENEUVE J.-P., S. DUCHESNE, A. MAILHOT, E. MUSSO and G. PELLETIER (1998). Évaluation des besoins des municipalités québécoises en réfection et construction d'infrastructures d'eaux, Rapport final. Institut national de la recherche scientifique, Sainte-Foy, Québec, Canada, 368 p.
- WALSKI T. and A. PELICCIA (1982) Economic analysis of water main breaks. JAWWA, 74(3), 140-147.
- WANG Y., T. ZAYED and O. MOSELHI (2009). Prediction models for annual break rates of water mains. J. Perform. Constr. Facil., 23(1), 47-54.
- YAMIJALA S., S.D. GUIKEMA and K. BRUMBELOW (2009). Statistical models for the analysis of water distribution system pipe break data. Reliab. Eng. Syst. Safe., 94(2), 282-293.
List of figures
Figure 1
Results of the calibrated models for the observation period from 1976 to 1996 and observed breaks (the WEE_ML_96 and WEEE_ML_96 curves overlap). LS: least squares; ML: maximum likelihood; 96: calibrations on the 1976-1996 period
Résultats des modèles calés avec les observations de la période 1976 à 1996 et nombre annuel de bris observés (les courbes WEE_ML_96 et WEEE_ML_96 sont superposées)
Figure 2
Results of the calibrated models for the observation period from 1976 to 2007 and observed breaks. LS: least squares; ML: maximum likelihood
Résultats des modèles calés avec les observations de la période 1976 à 2007 et nombre annuel de bris observés
Figure 3
Cumulative breaks from 1976 to 2007, observed and simulated with a second degree polynomial
Bris cumulés de 1976 à 2007, observés et simulés avec un polynôme du second ordre
Figure 4
Results for the derived model (AOAB), the WEEE_ML_07 model and the linear regression, compared to the observations from 1976 to 2007. ML: maximum likelihood
Résultats du modèle dérivé (AOAB), du modèle WEEE_ML_07 et de la régression linéaire, comparés avec les observations pour la période de 1976 à 2007
Figure 5
Simulation of the 0.5% pipe replacement scenario on the 1996 network and comparison with the WEEE_ML_96 model results, the WEEE_ ML_07 model results, and the observed breaks. ML: maximum likelihood
Simulation du scénario annuel de remplacement de 0,5 % de la longueur totale du réseau de 1996 et comparaison avec les résultats du modèle WEEE_ML_96, les résultats du modèle WEEE_ML_07 et les bris observés
Figure 6
Replacement scenarios simulated with the WEEE_ML_07 model
Scénarios de remplacement simulés avec le modèle WEEE_ML_07
List of tables
Table 1
Calibration parameter values for the period 1976 to 1996
Valeur des paramètres de calage pour la période 1976 à 1996
Table 2
Percentage of pipes according to the total recorded number of breaks
Pourcentage de conduites selon le nombre total de bris enregistrés
Table 3
Calibration parameter values for the period 1976 to 2007
Valeurs des paramètres de calage pour la période 1976 à 2007
Table 4
Predicted number of average annual breakages with the WEEE and AOAB models
Nombre annuel moyen de bris prédits avec les modèles EEE et AOAB
Table 5
Predicted number of average annual breakages with the WEEE model for different scenarios
Nombre annuel moyen de bris prédits avec le modèle WEEE pour différents scénarios
Table 6
Predicted annual number of breaks according to various pipe replacement scenarios (the indicated percentages correspond to the percentage of total length of the network)
Nombre annuel de bris simulés selon différents scénarios de remplacement de conduites (les pourcentages indiqués correspondent à des pourcentages de la longueur totale du réseau)