Résumés
Résumé
Cette étude met en évidence l’existence d’une relation coïntégrante de demande de monnaie dans les pays de la Commission économique et monétaire de l’Afrique centrale (CEMAC) en tenant compte d’une possibilité de changements structurels affectant les agrégats macroéconomiques. Elle se focalise ensuite sur la stabilité et l’homogénéité des comportements de demande de monnaie dans ces pays faisant face à une politique monétaire unique. Si leur stabilité ne peut être remise en cause, leur hétérogénéité peut par contre accroitre la dispersion de l’inflation dans ces différents pays.
Corps de l’article
Introduction
L’instabilité des agrégats monétaires observée à partir des années 1980, a été à l’origine de nombreuses mutations dans la formulation de la politique monétaire dans plusieurs pays développés. En effet, le développement spectaculaire des actifs liquides (tels que les fonds mutuels, les titres d’organismes de placement collectif en valeurs mobilières (OPCVM)…) a contribué à restreindre la limite entre actifs monétaires et non monétaires. Certains de ces actifs bien que s’agissant des valeurs mobilières, étaient utilisés comme réserve de moyen de paiement rendant ainsi plus complexe le contrôle des agrégats monétaires. À ce problème de contrôle s’ajoute celui de l’instabilité des fonctions de demande de monnaie, qui, incapables de prévoir et de rendre compte de la réalité, deviennent alors un guide inapproprié de la politique monétaire. Ainsi, la FED, comme bien d’autres banques centrales (Nouvelle-Zélande, Espagne, Canada, Royaume-Uni, Suède), a renoncé dès le début des années 1990 à l’utilisation d’un agrégat monétaire comme objectif intermédiaire de la politique monétaire. Dans les pays en développement en général, et ceux de la zone de la Commission économique et monétaire de l’Afrique centrale (CEMAC) en particulier, de telles instabilités monétaires ne sont pas encore mises en évidence ou semble ne pas susciter de préoccupations majeures. Pourtant, les économies de la sous-région ont connu différentes mutations et crises financières plus ou moins marquées susceptibles de « troubler » le comportement de demande de monnaie des agents. On peut citer la crise économique de la fin des années 1980 suite à l’effondrement des cours des produits de base, les réformes monétaires et financières opérées par la Banque des États de l’Afrique centrale (BEAC) en fin d’année 1990, la dévaluation de 50 % du franc CFA par rapport au franc français survenu en janvier 1994, l’ancrage du CFA à l’euro dès 1999, etc. Dans la même lignée, le développement récent des innovations financières telles que la monnaie électronique bien qu’embryonnaire, peut mettre à mal la stabilité de la demande de monnaie.
Par ailleurs, en réaction à la politique monétaire commune, les comportements de demande de monnaie sont-ils homogènes (d’un point de vue des élasticités) dans les différents pays de la zone CEMAC?
Objectif
Inspirée des fondements théoriques d’origine monétariste, l’utilisation d’un agrégat monétaire comme objectif intermédiaire de la politique monétaire repose sur l’hypothèse de l’existence d’une fonction d’encaisses réelles stable à long terme (Friedman, 1956). L’objectif de cet article est donc de vérifier à l’aide d’outils économétriques appropriés, l’existence ou non d’une relation coïntégrante de demande de monnaie dans les pays de la zone CEMAC. Il s’agira par la suite de déterminer si les différentes crises et mutations financières ci-dessus mentionnées ont eu un effet sur leurs qualités statistiques.
Méthodologie
Nous étudions l’existence d’une relation coïntégrante de demande de monnaie en tenant compte de la possibilité des ruptures structurelles sur la dynamique des séries macroéconomiques utilisées. Ces ruptures sont mises en oeuvre grâce au test de Bai et Perron (1998). Par ailleurs, Perron (1989) montre qu’en présence de tels changements structurels affectant la tendance des séries, les tests habituels de racine unitaire (test ADF) sont biaisés en faveur de l’hypothèse nulle. Afin d’étudier efficacement les propriétés stochastiques des variables, nous recourrons judicieusement au test de Zivot et Andrews, permettant de tester l’existence d’une racine unitaire compte tenu d’une rupture structurelle. Ces résultats sont enfin pris en compte dans l’étude multivariée de la coïntégration proprement dite, à travers la procédure de Johansen, Mosconi et Nielsen (2000) qui tient en effet compte d’un changement structurel dans la composante déterministe du modèle vectoriel à correction d’erreur (VECM).
1. Aperçu de la politique monétaire en zone CEMAC
La politique monétaire des six États membres de la CEMAC (Cameroun, Gabon, Guinée équatoriale, Congo, République centrafricaine (RCA)) est définie et conduite par la Banque des États de l’Afrique Centrale (BEAC) depuis le début des années 1970. Celle-ci, conformément à ses statuts, « émet la monnaie de l’union monétaire et en garantit la stabilité ». Concrètement, les objectifs finals de la politique monétaire sont d’assurer la stabilité monétaire par le maintien d’une faible progression de l’inflation et une forte couverture extérieure de la monnaie (meilleure constitution des réserves de change)[1]. La BEAC, comme bien d’autres banques centrales, a adopté un principe que l’on peut attribuer à la théorie monétariste : celui consistant à faire de la stabilité des prix, la priorité de la politique monétaire. Ce principe est théoriquement fondé : (i) il découle du fait que la stabilité des prix est reconnue comme la condition nécessaire pour garantir une évolution durable d’une économie le long de son sentier de croissance potentielle; (ii) il s’appuie ensuite sur le fait que lorsque les anticipations d’inflation à long terme sont fermes, la variabilité des taux d’intérêt à long terme est plus faible et il est plus facile pour les entreprises et les investisseurs de s’engager dans des contrats à long terme (Rogoff, 2003).
La BEAC vise ainsi une progression annuelle du taux d’inflation de l’ordre de 3 % maximum et pour ce faire, elle s’appuie sur deux objectifs intermédiaires : l’agrégat monétaire M2 et le crédit à l’économie dont les taux de croissance sont particulièrement suivis. Pour ce dernier indicateur, une valeur de référence compatible avec la stabilité des prix est de ce fait déterminée à moyen terme par la programmation monétaire. Pourquoi lier croissance monétaire et évolution des prix? Dans son livre Inflation et systèmes monétaire[2], Milton Friedman réhabilite par évidences empiriques la théorie quantitative de la monnaie. Dans cet ouvrage, Friedman affirme que : « la cause immédiate de l’inflation est toujours et partout la même : un accroissement anormalement rapide de la quantité de monnaie par rapport au volume de la production ». Le graphique 1 montre l’évolution annuelle de la masse monétaire et celle de l’inflation dans quatre pays de la zone CEMAC.
Bien qu’un examen visuel de ce graphique ne suffit pas à admettre une relation causale entre croissance monétaire et inflation, il nous permet néanmoins de constater que dans ces pays et la plupart de temps, des périodes d’accélération de l’inflation correspondent bien à des périodes de forte croissance de la masse monétaire[3]. Cette corrélation entre croissance monétaire et inflation a été étudiée par Barro, qui arriva à la conclusion selon laquelle « il existe une relation stable entre le taux d’inflation et le taux de croissance de la masse monétaire, à la fois synchronique c’est-à-dire entre les pays et à la même date, et diachronique c’est-à-dire dans le temps pour un même pays[4] ».
2. Quelques considérations théoriques
Les théories visant à expliquer les comportements de détention d’encaisses monétaires des agents non financiers ont fait l’objet d’une abondante littérature et diffèrent d’un auteur à l’autre. Ces divergences d’opinion découlent fondamentalement de la divergence de conceptions quant au rôle que joue la monnaie au sein de l’économie (intermédiaire des échanges, unité de compte, réserve de valeur). Pour les classiques (notamment Ricardo, Marx, Walras), toutes les marchandises peuvent être rapportées à une autre, cette dernière étant rapportée à elle-même : c’est le rôle que joue la monnaie, et Walras l’appelle numéraire. Comme telle, elle n’influence pas les grandeurs réelles; il y a donc une séparation entre la sphère réelle et la sphère monétaire : c’est la dichotomie classique. De cette hypothèse, découle celle de neutralité, reformulée par la théorie quantitative (Pigou, 1917 et Marshall, 1923). En effet, ces auteurs, partant d’une réflexion microéconomique établissent que pour un individu donné, la demande de monnaie est proportionnelle au niveau nominal de revenu (py), toutes choses égales par ailleurs, ce qui permet d’obtenir l’équation agrégée
Graphique 1
Évolution entre croissance monétaire et inflation en zone CEMAC
Dans l’équation (2.1), le terme k (inverse de la vitesse de circulation) reflète le volume des transactions, mais pourrait dépendre des facteurs tels que la richesse, le taux d’intérêt, etc. Par rapport à la sensibilité de la demande de monnaie au taux d’intérêt, Keynes (1936) fournit une explication plus convaincante[5] : La fonction keynésienne de demande de monnaie s’écrit :
avec Yp le revenu permanent. Cette version simplifiée donnée par l’expression 2.3 s’appuie sur les hypothèses d’homogénéité de degré 1 de la fonction de demande de monnaie par rapport au prix (absence d’illusion monétaire) et par rapport au revenu.
Par ailleurs, Baumol (1952) et Tobin (1956) ont développé une modélisation des comportements de demande de monnaie dans laquelle la monnaie est essentiellement vue comme un stock à des fins de transaction. Ils montrent que sous certaines hypothèses d’imperfection de marché, la demande de monnaie à des fins de transaction dépend du coût d’opportunité de détention de la monnaie et s’établit :
avec Md, la demande d’encaisses nominales et c, le coût de conversion d’une unité de titre en monnaie (les frais de courtages, par exemple). L’équation 2.4 est appelée square root equation. Dans le même ordre, la théorie de gestion de portefeuille dans un environnement risqué donne une équation de demande de monnaie de la forme :
avec re, rb, πa désignant respectivement le rendement réel attendu des actions, le rendement réel attendu des obligations et le taux d’inflation anticipé. L’ équation (2.5) amène une fois de plus à s’interroger : pourquoi les agents détiennent-ils de la monnaie au lieu d’orienter leur épargne vers l’achat des actifs « dominant » la monnaie tels que les titres du Trésor public par exemple? Certains chercheurs en ont conclu que la monnaie n’est pas « un bien comme tous les autres » (voir Kurmann, 2006), sinon son poids (sa demande) dans un portefeuille optimal d’actifs serait nul. Une façon donc de capter les services rendus par la monnaie à ses détenteurs est de l’introduire dans une fonction d’utilité (Money in the utility function), ou d’imposer une contrainte de paiement préalable en espèces (Cash in advance model). À ce sujet, voir Guillard (1999), McCalum et Goodfriend (1987).
3. Choix des variables et analyse stochastique des variables
3.1 Modèle de base
Conformément aux théories précédemment passées en revue, nous retenons une spécification de l’équation de long terme de la forme :
3.2 Choix des variables et signe attendu des coefficients
L’agrégat monétaire : il s’agit de la masse monétaire au sens large M2 constituée de la masse monétaire au sens strict M1 et de la quasi-monnaie. En effet, cette variable est suivie par la BEAC comme indicateur de la politique monétaire.
La variable d’échelle : le choix d’une variable d’échelle se base sur les théories économiques liant la demande de monnaie à une variable de transactions, et donc sa demande dépend de la richesse totale des individus (théorie du choix des portefeuilles, théorie friedmanienne). Dans ce sens, la richesse totale est une bonne mesure de la variable d’échelle. Elle est souvent approximée par le revenu permanent, mais cette dernière variable est rarement disponible. Ici, nous utilisons le PIB réel comme proxy de la variable de transaction. Conformément à la théorie économique selon laquelle la demande de monnaie avec le revenu, nous anticipons un signe positif pour le coefficient δ. On a δ = 1 dans les théories monétaristes et δ = 0,5 dans les théories de stock de Baumol et Tobin.
Le taux d’intérêt : afin de comprendre l’influence du taux d’intérêt sur la demande d’encaisses monétaires, il faudrait se détourner du rôle de monnaie comme moyen de paiement et la considérer comme un actif financier à part entière. Sa détention dépend alors de son prix relatif par rapport aux actifs alternatifs. Dans ce cas, le taux d’intérêt varie en sens inverse des encaisses monétaires. En effet, une augmentation des taux d’intérêt sur les actifs alternatifs amènent les agents non financiers à orienter leurs épargnes vers les placements plus rémunérateurs. Cette conception théorique sera tout au moins nuancée, du fait de l’absence de marchés financiers viables dans la zone CEMAC, qui exprime en d’autres termes la rareté des actifs alternatifs à la monnaie. Cela nous conduit à considérer judicieusement le taux d’intérêt sur les dépôts à terme comme le principal prix de détention de la liquidité. Du fait que ce taux rémunère des actifs monétaires intrinsèques à l’agrégat M2, il varie raisonnablement dans le même sens que les encaisses monétaires et nous conduit à anticiper un signe positif pour θ.
L’inflation anticipée : dans les pays en développement en général et dans la zone CEMAC en particulier, en l’absence de marchés financiers viables où les agents peuvent disposer de placements en actifs financiers alternatifs à la monnaie, l’acquisition des actifs réels apparaît souvent comme un moyen de se protéger contre l’inflation. De ce point de vue, il existe une relation négative entre le taux d’inflation et les encaisses monétaires, dans le sens où une persistance de l’inflation peut amener les agents à se débarrasser de la monnaie pour acquérir des biens physiques durables[6]. Le problème peut être aussi observé en sens inverse : en présence d’une hausse généralisée des prix, les agents doivent augmenter leurs encaisses monétaires pour couvrir leurs dépenses de transactions habituelles. Dans ce cas, on s’attend à ce le signe de µ soit positif.
Le taux d’intérêt étranger : dans une perspective de globalisation financière et de parfaite mobilité des capitaux, le taux de rendement espéré des actifs étrangers, peut paraître comme une variable de coût d’opportunité de détention de la monnaie locale[7].
3.3 Mise en évidence des ruptures structurelles
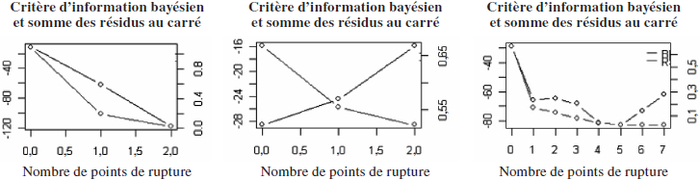
Les changements structurels sont mis en évidence par le test de Bai et Perron (1998) dont le principe est précisé dans la sous-section 1.3 de l’annexe. Ces tests de changement structurel sont réalisés à l’aide du logiciel R (progiciel «strucchange»). Le nombre optimal de ruptures ![]() est obtenu grâce au critère d’information BIC[8], et évidemment à l’aide de la minimisation de la somme des carrés des résidus (voir graphique 3). Les résultats sont synthétisés dans les tableaux 1 et 2 et où
est obtenu grâce au critère d’information BIC[8], et évidemment à l’aide de la minimisation de la somme des carrés des résidus (voir graphique 3). Les résultats sont synthétisés dans les tableaux 1 et 2 et où ![]() désigne le nombre optimal de ruptures.
désigne le nombre optimal de ruptures.
Tableau 1
Test de changement structurel sur les séries camerounaises et gabonaises
Note : * (respectivement **), signifie un changement de tendance (respectivement de constante et de tendance) dans l’évolution de la série.
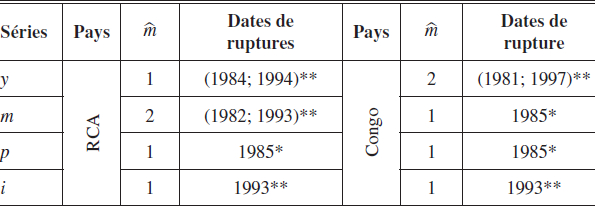
Tableau 2
Test de changement structurel sur les séries centrafricaines et congolaises
Note : * (respectivement **), signifie un changement de tendance (respectivement de constante et de tendance) dans l’évolution de la série.
Graphique 2
Ruptures structurelles au Cameroun et au Gabon
Graphique 3
Critère de détermination du nombre optimal de partitions
Il ressort du tableau 1, que les séries ont été affectées de changements structurels de taux de croissance ou de niveau. Pour le Cameroun, les dates de rupture se situent aux environs des années 1985 et 1986 d’une part, et autour des années 1993 et 1994, d’autre part. Ces dates renvoient respectivement à la crise économique et financière survenue en 1986 et à la dévaluation de 1994. Dans le cas du Gabon, les mêmes dates semblent revenir : les impacts de la crise économique et de la dévaluation se font ressentir. La date de 1998 peut être rattachée aux effets de la crise financière asiatique de 1999. seule la date 1976 ne nous semble pas économiquement interprétable. Le graphique représente quelques séries ainsi que les dates de ruptures.
Le même test est effectué pour les séries de la RCA et du Congo. Ces résultats sont consignés dans le tableau 2. On peut noter que les dates 1982, 1984, 1985, 1993 et 1994 sont identifiées pour la RCA, comme des années où les séries auront connu des chocs significatifs. Plus précisément, les années 1984 et 1994 correspondent aux dates où le PIB réel connaît une forte croissance positive (9,48 % en 1984 contre 4,9 % en 1994) après plusieurs années de croissance négative[9]. L’année 1985 correspond à la date où l’inflation culmine à 34 % et connaîtra une chute importante l’année suivante. De même, les années 1982 et 1993 correspondent à une accélération de la croissance monétaire. À l’aide des mêmes procédures, le test détecte les années 1981, 1985, 1993 et 1997 comme dates de changement structurel au Congo. Si l’année 1981 ne nous semble pas liée à un évènement notable dans l’économie congolaise, c’est moins vrai pour les autres. En effet, les années 1985 et 1993 précèdent les grands évènements majeurs à savoir la crise économique de 1986 et la dévaluation de 1994. De même, l’année 1997 correspond au début de la guerre civile au Congo. Certaines de ces séries sont représentées sur le graphique 4, ainsi que les dates de ruptures correspondantes.
En présence de ruptures dans la tendance de données, il est à noter que les tests usuels de racine unitaire (test ADF par exemple) peuvent conduire à des rejets à tort de l’hypothèse alternative. Dans la littérature, il existe plusieurs tests de racine unitaire tenant compte d’une possibilité de rupture dans la tendance de la série. Nous pouvons citer à ce titre, le test de Perron et Ogelsang (1992), de Bai et Perron (1997), de Banerjee et al. (1992), de Zivot et Andrews (1992). Les deux derniers cités permettent de différencier un processus stationnaire avec rupture structurelle d’un processus avec racine unitaire en tenant compte de la possibilité de rupture dans le processus générateur des données sous l’hypothèse alternative. Dans ce travail, nous privilégions le test de Zivot et Andrews (1992) en raison de sa disponibilité dans certains logiciels[10].
Graphique 4
Ruptures structurelles en RCA et au Congo
3.4 Test de racine unitaire avec prise en compte des ruptures : le test de de Zivot et Andrews
Zivot et Andrews (1992), considèrent pour une série {yt}t=1,...,T, l’hypothèse nulle selon laquelle la série possède une racine unitaire sans changement structurel exogène.
Sous H0, on a :
L’hypothèse alternative est celle de l’existence d’une stationnarité autour d’une tendance, avec un changement structurel survenu à une date inconnue Tb sur le niveau de la série, la pente ou les deux. Cela revient à distinguer trois variantes sous l’hypothèse alternative, correspondant à trois modèles semblables à ceux de Perron (1989). Les équations de régressions sont donc celles de Dickey et Fuller modifiées dont les contours sont largement présentés en annexe.
Ce test a été appliqué et les principaux résultats sont synthétisés dans les tableaux suivants (tableaux 3 et 4) dans lesquels ![]() représente la date de rupture estimée et tmin, la valeur minimale de la statistique-t associée à ρ. La décision sur l’ordre d’intégration de la série est donnée après une éventuelle différenciation. Le test de Zivot et Andrews détecte formellement la présence d’une seule rupture, mais certains auteurs l’adaptent de manière à ce qu’il puisse rendre compte d’une présence éventuelle de plusieurs ruptures, ceci en représentant la courbe des valeurs de la statistique-t associée à ρ et en retenant graduellement les dates correspondant aux minimas de cette courbe (voir par exemple Goux, 2005). Une deuxième date de rupture si elle est ainsi détectée sera représentée dans le tableau et mise entre parenthèse.
représente la date de rupture estimée et tmin, la valeur minimale de la statistique-t associée à ρ. La décision sur l’ordre d’intégration de la série est donnée après une éventuelle différenciation. Le test de Zivot et Andrews détecte formellement la présence d’une seule rupture, mais certains auteurs l’adaptent de manière à ce qu’il puisse rendre compte d’une présence éventuelle de plusieurs ruptures, ceci en représentant la courbe des valeurs de la statistique-t associée à ρ et en retenant graduellement les dates correspondant aux minimas de cette courbe (voir par exemple Goux, 2005). Une deuxième date de rupture si elle est ainsi détectée sera représentée dans le tableau et mise entre parenthèse.
Tableau 3
Résultats du test de Zivot-Andrews sur les séries camerounaises et gabonaises
Note : Une date suivie de ** (respectivement *) signifie un changement de constante et de tendance, (respectivement, changement de tendance), sinon changement de constante.
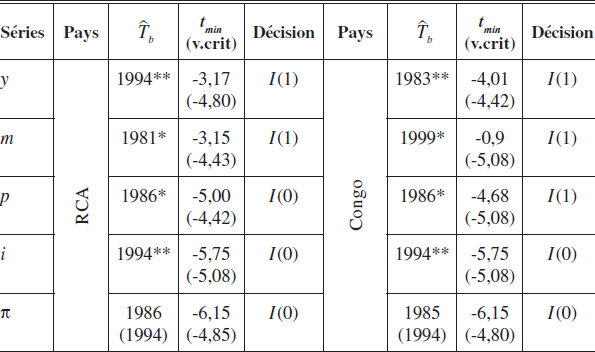
Tableau 4
Résultats du test de Zivot-Andrews sur les séries centra fricaines et congolaises
Note : Une date suivie de ** (respectivement *) signifie un changement de constante et de tendance, (respectivement, changement de tendance), sinon changement de constante.
Le tableau 3 nous rend compte des dates de ruptures au Cameroun et au Gabon. Ces dates ne sont pas fondamentalement différentes de celles trouvées à la section précédente.
De même, le tableau 4 présente la situation en RCA et au Congo. Les deux dates de choc majeur sont une fois de plus révélées, à l’exception des dates de rupture sur la croissance de M2, qui est de 1981 pour la RCA et de 1999 pour le Congo.
L’analyse précédente montre l’importance de tenir compte des ruptures structurelles susceptibles d’affecter l’évolution des séries, ceci afin d’avoir entres autres, de plus amples connaissances sur la nature stochastique des variables. Ces résultats seront pris en compte dans la section suivante portant sur l’analyse coïntégrante des séries.
4. Principe méthodologique de la coïntégration
Les outils économétriques relatifs à l’étude de demande de monnaie ont beaucoup évolué depuis l’abandon des modèles d’ajustement partiel vers la fin des années 1970, après que ceux-ci aient démontré plusieurs insuffisances, notamment leur incapacité à expliquer les périodes troubles des années 1973. La théorie de la coïntégration paraît alors de nos jours comme un outil important de l’étude des relations d’équilibre de long terme entre plusieurs grandeurs macroéconomiques, notamment dans l’étude de la parité de pouvoir d’achat (Johansen et Juselius, 1990; Kugler et Lenz, 1993), du taux de change entre divers pays (Goux, 2005), ou de demande de monnaie (Johansen et Juselius, 1990; Hendry, 1995). L’idée à la base du principe de coïntégration est qu’une ou plusieurs relations de long terme peuvent être définies entre plusieurs variables, pourtant individuellement non stationnaires. De telles variables, même si elles évoluent à court terme dans des directions différentes, seront ramenées à long terme les unes « proches » des autres par des forces économiques telles qu’un mécanisme de marché ou une intervention publique (Granger, 1986).
Introduite substantiellement par Engle et Granger (1987), la notion de coïntégration a dans le temps évolué pour prendre en compte plusieurs relations de long terme. Le modèle statistique développé à cet effet par Johansen (1988), puis Johansen et Juselius à partir des années 1990 s’appuie sur un VAR à correction d’erreur (VAR-ECM ou VECM).
4.1 Présentation du modèle statistique
Le modèle statistique est un VAR d’ordre k, dont la forme réduite est formulée par l’équation suivante :
avec Xt un vecteur colonne de variables d’intérêt de dimension p : X′t = (mt, yt, pt, it, πt, i*t) dans le cas présent. µ et η représentent respectivement les matrices de constantes et de tendances de dimension p × 1. ![]() ; le terme d’erreur de dimension p × 1 supposé normal et indépendamment distribué, de moyenne nulle et de matrice de variance-covariance non singulière Σ. φ1, ..., φk sont des matrices de coefficients de dimensions p × p, contenant les paramètres du modèle. Dt est un vecteur de variables non stochastiques (qui peuvent désigner la tendance temporelle, des variables muettes saisonnières, etc.).
; le terme d’erreur de dimension p × 1 supposé normal et indépendamment distribué, de moyenne nulle et de matrice de variance-covariance non singulière Σ. φ1, ..., φk sont des matrices de coefficients de dimensions p × p, contenant les paramètres du modèle. Dt est un vecteur de variables non stochastiques (qui peuvent désigner la tendance temporelle, des variables muettes saisonnières, etc.).
Quelques arrangements algébriques permettent d’écrire la relation (4.1) sous la forme d’un modèle vectoriel à correction d’erreur (VECM) de la manière suivante :
avec :
les Γi contiennent les paramètres de court terme et Π les paramètres de long terme estimés par la méthode de maximum de vraisemblance. L’idée intuitive sous-tendant l’écriture sous la forme (4.2) est que si les composantes de Xt sont coïntégrés, non seulement la représentation sera stationnaire en différence à court terme, mais également elle le sera en niveau à long terme. Tous les termes non déterministes de l’équation (4.2) sont I(0), à l’exception de Π Xt-k . L’hypothèse de coïntégration se fonde donc sur les propriétés de la matrice Π, et notamment sur la condition reposant sur la réduction de son rang. Trois cas sont à distinguer :
rang(Π) = 0 : cela correspond au cas où il n’existe aucune relation de coïntégration et le modèle n’a aucune propriété de long terme;
rang(Π) = p : dans ce cas, Π est de plein rang, et correspond à une situation où toutes les composantes de Xt sont stationnaires;
rang(Π) = r, avec 0 < r < p : dans ce cas, la matrice Π peut se décomposer sous la forme Π = αβ′ , où α et β sont des matrices de plein rang de dimension p × r.
Cette dernière hypothèse implique que Xt est non stationnaire, mais que β′Xt est stationnaire et peut être interprétée comme la relation de coïntégration ou de long terme (voir Johansen et Juselius, 1991). Dans ce cas, r est le nombre de relation de coïntégrations et α la matrice des poids. Ses r colonnes linéairement indépendantes définissent les paramètres d’ajustement et mesurent la vitesse de convergence vers l’équilibre de long terme. β est le vecteur coïntégrant, ses r colonnes linéairement indépendantes définissent les r relations de long terme. Johansen (1988) formule l’hypothèse d’existence de r relations de coïntégration par :
La spécification du terme déterministe permet de prendre en compte la présence ou non d’une constante ou tendance linéaire dans les relations de long terme ou de court terme.
4.1.1 Test de rang de coïntégration
Deux types de tests basés sur le ratio de vraisemblance sont proposés par Johansen et Juselius (1990) pour déterminer le nombre de relations de coïntégration. Le premier appelé test de la trace, teste la coïntégration de rang r contre la stationnarité des séries et se formule par : H0 : rang Π = r versus H1 : rang Π = p.
La statistique de la trace [notée λ-trace(r)] est donnée par :
avec Q le ratio de vraisemblance. Le deuxième, appelé test de la valeur propre maximale, teste l’existence de r relations de long terme, contre l’ajout d’une relation supplémentaire de coïntégration. Il se formule par :
La statistique de ce test [notée λmax(r)] est donnée par :
4.1.2 Les tests de restriction linéaire
Tests de restriction sur les vecteurs coïntégrants
Les tests d’usage courant portent sur la restriction des paramètres de long terme suggérés par les théories économiques. C’est par exemple le cas lorsque nous aurions à tester économétriquement l’homogénéité de la demande de monnaie par rapport au prix ou par rapport au revenu (en imposant l’égalité à 1 de leurs élasticités). Ce test est formalisé par :
H est une matrice de dimension p × s imposée par le modélisateur et traduisant la relation à tester. ϕ est une matrice de dimension s × r à estimer avec r ≤ s ≤ p.
Johansen et Juselius (1991) proposent un ratio de vraisemblance pour tester l’hypothèse H2 contre H1, (notée –2 log Q (H2 / H1)) qui est distribuée asymptotiquement suivant un χ2 (p – s) × r degrés de liberté.
Tests sur les paramètres d’ajustement
Un autre type de restriction peut porter sur la matrice des poids α. Par exemple, sur la nullité d’une ligne de α correspondant à l’absence de poids dans les relations de coïntégration pour une variable (cas de l’exogéneité faible). Ces restrictions sont imposés sur les poids α au moyen d’une matrice A imposée par l’utilisateur. Plus formellement, le modèle s’écrit :
A est une matrice de dimension p × l, avec r ≤ l ≤ p. La statistique de ce test est donnée par –2 log Q (H3 / H1) et est asymptotiquement distribuée suivant un χ2 à (p – l) × r degrés de liberté[11].
On peut aussi tester la restriction conjointe sur les matrices α et β. Ces types de tests sont conçus par combinaison des deux tests précédents et formalisés par :
4.1.3 L’introduction des ruptures structurelles
La démarche classique que nous venons de décrire peut produire des résultats peu satisfaisants car la non-prise en compte des chocs majeurs dans la dynamique des données peut avoir des répercussions négatives sur la qualité du modèle ou même conduire à rejeter à tort l’hypothèse de coïntégration (voir Goux, 2005). En plus, elle ne nous permet pas de rendre compte de l’impact de ces évènements exogènes. L’approche proposée par Johansen, Mosconi et Nielsen (2000) surmonte cette insuffisance et permet de prendre en compte des ruptures dans la composante déterministe du VECM.
5. Données et stratégie d’estimation
Les données vont de 1972 à 2006. L’année 1972 correspond à la date d’entrée en vigueur de la BEAC. Les taux d’intérêt national et étranger sont issus du IFS du Fonds monétaire international. Les autres séries quant à elles proviennent du World Developpement Indicator de la Banque mondiale. L’estimation du VECM se fait avec constante dans l’espace de coïntégration et dans le VAR en différence. La mauvaise complétude de données pour le Tchad et la Guinée équatoriale nous amène à exclure ces deux pays dans la suite des estimations. Le vecteur de variables endogène est défini par Xt = (mt, pt, yt, it, πt, i*t)′. Les analyses se font suivant la stratégie suivante : 1-test de coïntégration; 2-estimation du VECM; 3-observation des résidus; 4-test de normalité et de bruit blanc des résidus; 5-introduction des dates de ruptures si nécessaires. Nous imposons ensuite les restrictions jusqu’à ce que tous les vecteurs coïntégrants soient identifiés[12]. En cas d’existence de plusieurs relations de coïntégration, nous décidons d’identifier par ailleurs la fonction de réaction de la banque centrale ou la relation de parité d’intérêt non couverte (PINC). La fonction de réaction s’exprime par it = θ0 + θ1πt + θ2yt + ΩZt + ∈t en supposant constants la croissance potentielle et le niveau d’inflation désiré. Zt est un ensemble de variables additionnelles susceptibles d’influencer la décision des autorités monétaires au moment où elles fixent le taux d’intérêt[13]. Les θi désignent le poids accordé par les autorités monétaires à chaque variable. Les coefficients trouvés par Taylor dans le cas de la Réserve fédérale sont θ1 = 1,5 et θ2 = 0,5. La PINC en régime de change fixe et sous l’hypothèse de mobilité parfaite de capitaux s’exprime par it – i*t = c0 + ωt, ω un bruit blanc. Tous les tests sont effectués au seuil 5 %.
6. Résultats de l’estimation
Afin de corriger le défaut de normalité et prendre en compte les ruptures structurelles, nous avons introduit des variables muettes exogènes définies par du94 = 1{1994≤t≤2006} dans le modèle des quatre pays en plus des spécifiques pour chaque pays; du86 = 1{1972≤t≤1986} pour le Cameroun et le Congo; du82 = 1{1972≤t≤1982} pour la RCA. Ces dates de rupture sont issues des résultats du test de Bai et Perron (voir sous-section 4.3).
6.1 Équations de long terme
Les paramètres de long terme identifiés sont présentés dans le tableau 5 de la page suivante.
6.1.1 La fonction de demande de monnaie
Homogénéité prix et revenu
On note une homogénéité-prix de la demande de monnaie dans tous les pays (élasticité prix unitaire). Les encaisses nominales croissant dans les mêmes proportions que les prix, nous sommes en situation d’absence d’illusion monétaire à long terme. Une élasticité unitaire du revenu est également observée dans tous les pays à l’exception de la RCA. Dans les autres pays, l’équation de la demande de monnaie peut donc s’exprimer comme une équation de vitesse de circulation de la monnaie.
Influence du taux d’intérêt national et de l’inflation
Les différents coefficients liés au taux d’intérêt présentent le signe attendu[14]. Une hausse des taux créditeurs amène les agents non financiers à détenir logiquement plus de monnaie à travers les dépôts rémunérés. Par contre la négativité des coefficients liés au taux d’inflation (excepté en RCA) induit une baisse d’encaisses nominales en cas de hausse de l’inflation. Cela correspond à une situation où toute tendance haussière de l’inflation amène les agents non financiers à substituer de la monnaie aux biens physiques. Par ailleurs, au Cameroun et au Gabon, le taux d’intérêt réel s’impose comme déterminant de la demande de monnaie (β(i) = – β(π)).
Tableau 5
Vecteurs coïntégrants
Note : Ces restrictions identifient tous les vecteurs coïntégrants; les t-statistic sont entre paranthèses.
Le taux d’intérêt étranger
Le taux d’intérêt étranger n’a pas une influence significative dans les comportements de demande de monnaie au Congo et au Gabon. A contrario, celui-ci a un effet négatif et significatif au Cameroun et en RCA. Il revient donc à dire qu’en cas de hausse du taux d’intérêt étranger (français), on assiste à une diminution des encaisses monétaires toutes choses étant égales d’ailleurs. Cette situation peut être assimilée à une fuite de capitaux. En cas de hausse du taux d’intérêt étranger, la BEAC ajuste toujours son taux d’intérêt directeur au-dessus de celui-ci afin de soutenir la fixité de la parité du franc CFA autour du niveau fixé.
Prenant en compte les propriétés ci-dessus, la fonction de demande de monnaie peut donc s’interpréter comme une équation de vitesse de circulation de la monnaie dans les cas du Cameroun, du Congo et du Gabon :
et comme fonction d’encaisses réelles dans le cas de la RCA :
6.1.2 La fonction de réaction de la banque centrale
L’une des relations de coïntégration a été identifiée comme la fonction de réaction de la banque centrale (voir tableau 5). Dans le cas du Cameroun et du Congo les coefficients liés au taux d’inflation et au revenu sont similaires à ceux trouvés par Taylor (respectivement 1,5 et 0,5). On note également une influence significative du taux d’intérêt étranger dans la fonction de réaction.
6.1.3 La parité d’intérêt non couverte
La PINC (troisième relation de coïntégration) n’est pas conforme à la spécification attendue : c’est-à-dire que le différentiel d’intérêt est uniquement fonction d’une prime de risque constant et d’un bruit blanc. Cette situation peut être justifiée par la situation où l’hypothèse de mobilité parfaite de capitaux est violée en raison du triangle d’incompatibilité de Mundell. En effet, compte tenu de la fixité de la parité entre le franc CFA et la monnaie française (aujourd’hui l’euro), et face à une politique monétaire non unique entre la France et la zone CEMAC, la mobilité des capitaux ne peut être parfaite entre les deux zones.
Tableau 6
La matrice des poids
6.2 Équation de court terme et impact des chocs structurels
La matrice des poids est présentée dans le tableau 6 dans lequel les chiffres marqués d’un astérisque constituent les poids significatifs au seuil de 5 %. Dans le cas du Cameroun, une déviation à la hausse de la demande de monnaie par rapport à l’équilibre de long terme s’ajuste par une baisse du taux d’intérêt étranger et de la masse monétaire la période suivante. L’ajustement vers l’équilibre de long terme est plus rapide par le biais du taux d’intérêt étranger que par celle de l’agrégat monétaire. Pour le Congo, on observe un ajustement lent vers l’équilibre de long terme par le biais d’une hausse des taux d’intérêt nationaux ou internationaux. Dans le cas du Gabon, tout excédent monétaire par rapport à la cible de long terme est résorbé la période suivante par un ajustement rapide et à la baisse du taux d’intérêt. À l’opposé, on peut identifier dans chaque pays étudié, plusieurs variables faiblement exogènes à court terme (α = 0), en l’occurrence le revenu y et la variable de prix p. Le poids associé à ces variables est nul et par conséquent, celles-ci ne participent pas au mécanisme de correction d’erreur en cas de déviation par rapport à la cible de long terme. Cette exogéneité faible à court terme peut être en partie due à l’effet des variables de rupture dans le modèle. De façon générale, tout déséquilibre monétaire est corrigé par un ajustement des variables du secteur monétaire (taux d’intérêt ou masse monétaire).
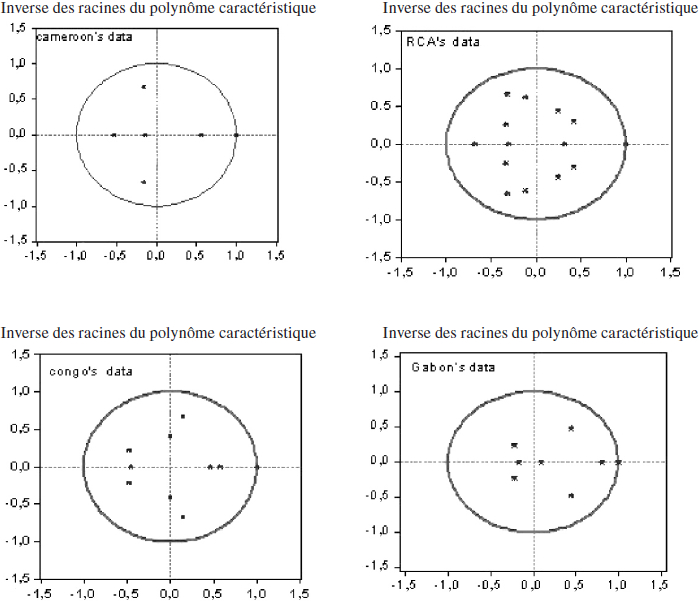
Nous avons limité notre attention aux équations de court terme liées à la demande de monnaie et en faisant abstraction des valeurs retardées des variables endogènes qui ne présentent pas grand intérêt ici (voir tableau 7). Nous notons une influence significative et positive dans tous les pays (excepté le Congo) de la dévaluation du franc CFA de 1994 sur les comportements de demande de monnaie à court terme. Cet effet se traduit par une hausse de demande de monnaie entre 26 % et 55 % selon les pays. Par contre, la crise économique de 1986 a eu des répercussions sur le Cameroun entrainant un ajustement des comportements des agents non financiers de près de 38 %. Pour autant, le graphique 5 présenté en annexe montre que le système est resté stable dans chacun des pays étudié malgré l’impact de ces chocs exogènes.
Tableau 7
Paramètres de court terme
Conclusion
L’étude que nous venons de réaliser met en évidence l’existence d’une relation coïntégrante de demande de monnaie dans les pays de la zone CEMAC[15] en tenant compte d’une possibilité de changements structurels affectant les agrégats macroéconomiques utilisés. L’hypothèse d’élasticité unitaire du revenu est vérifiée dans tous les pays étudiés excepté le cas de la RCA. De même, la neutralité à long terme de la monnaie ne peut être rejetée dans les pays étudiés. Par ailleurs, le taux d’intérêt réel s’avère, pour la plupart des pays, un déterminant de la demande de monnaie. En effet, la semi-élasticité liée au taux d’intérêt reste significativement positive et varie entre 35 % et 63 %. Les comportements de demande de monnaie ne correspondent donc pas à la version la plus extrême de la théorie quantitative. Cette influence significative du taux créditeur sur la demande de monnaie n’est pas surprenante dans un contexte économique marqué par l’absence ou la rareté des actifs financiers alternatifs à la monnaie. Enfin, la mise en évidence de l’hétérogénéité des comportements de demande de monnaie (d’un point de vue des élasticités) dans les pays de la zone CEMAC, devrait inciter les autorités monétaires à tenir compte des spécificités nationales. Cette hétérogénéité témoigne des effets différents de la politique monétaire à l’intérieur de chaque pays, et peut en effet se traduire par une hausse de la dispersion du taux d’inflation dans la zone.
Parties annexes
Annexe
A.1 Test de coïntégration et d’autocorrélation des résidus
Tableau 8
Test de coïntégration
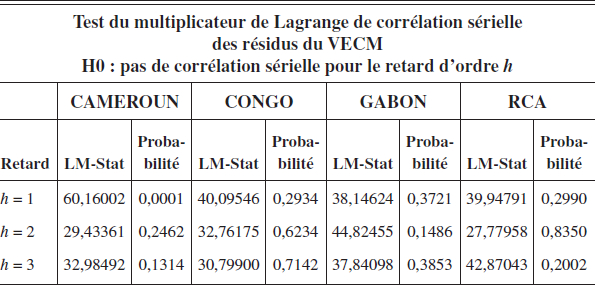
Tableau 9
Test d’autocorrélation des résidus
Graphique 5
Stabilité du VECM
A.2 Résultat du test de Bai et Perron appliqué aux séries utilisées
Graphique 6
Séries du Cameroun
Graphique 7
Séries du Gabon
Graphique 8
Séries RCA
A.3 Le test de changements structurels de Bai et Perron
A.3.1 Le modèle
On considère une série {yT}t=1,...,T , où l’on suppose l’occurrence de m ruptures structurelles survenues à des dates T1, ..., Tm inconnues. Pour chaque m-partition (T1, ..., Tm) de 1, ..., T, on considère le modèle de régression linéaire suivant :
avec l’hypothèse conventionnelle T0 = 0, et Tm+1 = T. zt ∈ℜq est le vecteur de régresseurs (exemple : zt = {1} pour un changement de constante, zt = {t} pour un changement de tendance). (δ1, ..., δm+1) est le vecteur de coefficients (avec δj, ≠ δj+1) et ut le terme d’erreur. Sous forme matricielle, l’équation (A.1) s’écrit :
Z̅ = Diag((Z1, ..., ZT)′), où Zi = (zTi-1, ..., zTi)′. Les estimateurs ![]() des coefficients
des coefficients ![]() sont obtenus par les MCO en minimisant la somme des carrés des résidus
sont obtenus par les MCO en minimisant la somme des carrés des résidus
Graphique 9
Séries du Congo
Graphique 10
Les taux d’intérêt
Le problème consiste à donner les estimateurs ![]() des vraies dates de rupture (T01, ..., T0m). On fait l’hypothèse de l’existence d’au moins un écart h entre deux dates de ruptures consécutives, c’est-à-dire ǀTj+1 – Tj ǀ≥ h ou de manière équivalente que ǀλj+1 – λj ǀ≥ ∈, ∈ fixé.
des vraies dates de rupture (T01, ..., T0m). On fait l’hypothèse de l’existence d’au moins un écart h entre deux dates de ruptures consécutives, c’est-à-dire ǀTj+1 – Tj ǀ≥ h ou de manière équivalente que ǀλj+1 – λj ǀ≥ ∈, ∈ fixé. ![]() est la fraction de la rupture. On pose :
est la fraction de la rupture. On pose :
Λ∈ = {(λ1, ..., λm) : ǀλj+1 – λj ǀ≥ ∈, λ1 ≥ ∈, λm+1 ≤ ∈}. Les estimateurs ![]() sont obtenus par balayage exhaustif de Λ∈ et déterminés par la minimisation de la somme des résidus sur toutes les m-partitions de (1, ..., T) telles que définies précédemment, c’est-à-dire :
sont obtenus par balayage exhaustif de Λ∈ et déterminés par la minimisation de la somme des résidus sur toutes les m-partitions de (1, ..., T) telles que définies précédemment, c’est-à-dire :
Les propriétés de convergence des estimateurs ![]() vers leurs vraies valeurs ainsi que leurs distributions asymptotiques sont données dans Bai et Perron (1998). Lorsque m > 2 , la méthode de balayage devient plus complexe et nécessite un temps de calcul important. Pour contourner la difficulté, Bai et Perron (1998), ont développé un algorithme basé sur les principes de programmation dynamique permettant l’obtention des minimas globaux en effectuant des MCO d’ordre O(T2) pour tout T ≥ 2 [16].
vers leurs vraies valeurs ainsi que leurs distributions asymptotiques sont données dans Bai et Perron (1998). Lorsque m > 2 , la méthode de balayage devient plus complexe et nécessite un temps de calcul important. Pour contourner la difficulté, Bai et Perron (1998), ont développé un algorithme basé sur les principes de programmation dynamique permettant l’obtention des minimas globaux en effectuant des MCO d’ordre O(T2) pour tout T ≥ 2 [16].
A.3.2 Estimateur du nombre optimal de ruptures
La sélection du nombre optimal m0 de ruptures est basée sur la minimisation des critères d’information[17] : Schwartz (1978)
avec p* = (m + 1) q + m.
Yao (1978) (critère d’information bayésien)
A.4 Le test de Zivot et Andrews
Zivot et Andrews (1992), considèrent pour une série {yt}t=1,...,T, l’hypothèse nulle selon laquelle la série possède une racine unitaire sans changement structurel exogène.
Sous H0, on a :
L’hypothèse alternative est celle de l’existence d’une stationnarité autour d’une tendance, avec un changement structurel survenu à une date inconnue Tb. Cela revient à distinguer trois variantes sous l’hypothèse alternative, correspondant à trois modèles semblables à ceux de Perron(1989). Les équations de régressions sont donc celles de Dickey et Fuller modifiées et s’écrivent de la manière suivante :
avec  et
et ![]() L’idée est d’estimer la date de rupture qui donne le plus grand poids à l’hypothèse alternative de stationnarité autour de la tendance. Une méthode possible est de retenir le point de rupture qui donne la statistique de student tρ=1 minimale, quand les petites valeurs de la statistique conduisent à rejeter l’hypothèse nulle. Si l’on note une
L’idée est d’estimer la date de rupture qui donne le plus grand poids à l’hypothèse alternative de stationnarité autour de la tendance. Une méthode possible est de retenir le point de rupture qui donne la statistique de student tρ=1 minimale, quand les petites valeurs de la statistique conduisent à rejeter l’hypothèse nulle. Si l’on note une ![]() telle valeur, l’on a par définition
telle valeur, l’on a par définition
Λ est un sous-ensemble fermé de [0,1]. Les statistiques-t et la date de rupture sont obtenus par les moindres carrés ordinaires après T – 2 régressions, avec λ parcourant en fait les valeurs de ![]() . On rejette l’hypothèse nulle de racine unitaire si
. On rejette l’hypothèse nulle de racine unitaire si
kiα, est la valeur critique tabulée au seuil α.
Notes
-
[1]
Le taux minimal de couverture extérieure de la monnaie est fixé à 20 %.
-
[2]
Milton Friedman (1969), Inflation et systèmes monétaires, p. 44.
-
[3]
Il faut noter qu’une accélération de l’inflation peut aussi être due à la hausse des produits énergétiques, d’où la nécessité d’établir une différence entre l’inflation et l’inflation sous-jacente qui semble plus appropriée dans ce cas.
-
[4]
Cité par Goux (1998).
-
[5]
The General Theory of Employment, Interest and Money.
-
[6]
Voir par exemple Kigabo et Goux (2007)
-
[7]
Voir par exemple Nachega (2001), ou Koulet-Vickot (2002).
-
[8]
C’est ce critère qui est disponible dans le logiciel R.
-
[9]
Ces chiffres sont calculés à partir des données.
-
[10]
Ce test est implémenté sous R, dans le progiciel « urca ».
-
[11]
Voir Johansen et Juselius 1991.
-
[12]
On estime à au moins r2 le nombre de restrictions linéaires qu’il faut imposer pour une identification complète des paramètres coïntégrants.
-
[13]
Voir Talabong et al. (2009) : « Fonction de réaction de la banque centrale et crédibilité de la politique monétaire », MPRA paper.
-
[14]
Les signes des coefficients présentés dans le tableau correspondent aux inverses de ceux de long terme.
-
[15]
Certains pays, notamment le Tchad et la Guinée équatoriale n’ont pas été pris en compte les données étant incomplètes.
-
[16]
Voir Bai et Perron (1998).
-
[17]
Le nombre optimal de ruptures peut aussi être testé à partir d’un test séquentiel, d’un test de type supF (voir Bai et Perron, 1998).
Bibliographie
- Avouyi-Dovi, S., A. Diop, E.-C. Fonteny, E. Gervais, P. Jacquinot, J.-S. Mesonnier et J.-G. Sahuc(2003), « Estimation d’une fonction de demande demonnaie pour la zone euro : une synthèse desrésultats », Bulletin de la banque de France, 111.
- Bai, J. et P. Perron (2003a), « Computation and Analysis of Multiple Structural Change Models », Journal of Applied Econometrics, 18 : 1-22.
- Bai, J. et P. Perron (2003b), « Critical Values for Multiple Structural Change Tests », Econometrics Journal, 6 : 72-78.
- Bai, J. et P. Perron(2001), « Multiple Structural Change Models: A SimulationAnalysis ». Unpublished manuscrit, Department of Economics,Boston University.
- Bai, J. et P. Perron (1998), « Estimating and Testing Linear Models With Multiple Structural Changes », Econometrica, 66 : 47-78.
- Bernard, A. et G. Roy(2003), « Étude des distorsions de niveau des testsde Johansen pour la coïntégration », Cahiers de recherche, W/P: 03-08, Université de Sherbrooke.
- Bhaskara, R et S. Rup(2004), « A Cointegration and Error Correction Approach toDemand for Money in Fiji: 1971-2002 », Working Paper, n°2004/11, The University of the South Pacific Suva, Fiji Islands.
- Bordes, C., H. Chevrou-Séverac et V. Marimoutou(2001), « Une Europe monétaire à plusieursvitesses? La demande de monnaie dans les grands pays de la zone euro(1979-1999) », Économie et Prévision, 147 : 51-71.
- Creel, J. et H. Sterdyniak (1999), « Pour en finir avec la masse monetaire », Revue Économique, 50(3) : 523-533.
- Dickey, D. et W. Fuller (1981), « Likelihood Ratio Statistics for Autoregressive Time Series with Unit Root », Econometrica, 49(4) : 1057-1072.
- Golfeld, S.M. et D.E. Sichel (1990), « The Demand for Money », in B.M. Friedman et F.H. Hahn (éds), Handbook of Monetary Economics, 1 : 299-356.
- Goux, J.F. (2005), « Le taux de change euro-dollar : une approche fondée sur la coïntégration avec break structurel », La Documentation française, 3(103) : 45-72
- Goux, J.F. et T. Rusuhuzwa Kigabo (2007), « Rupture structurelle et demande de monnaie au Rwanda ».
- Goux,J.F. (2000), « Existe-t-il vraiment une relationcoïntegrante de demande de monnaie M3 en France? », Revue Économique, 51(4) : 885-911.
- Goux, J.F. (1998), inflation, désinflation, déflation, Dunod.
- Guillard,M. (1999), « La monnaie dans les modèles de choixintertemporels : quelques résultatsd’équivalences fonctionnelles », document derecherche, Centre d’étude des politiqueséconomiques de l’Université d’Evry.
- Johansen, S. et K. Juselius(1990), « Maximum Likelihood Estimation and Inference onCointegration with Applications to the Demand for Money », Oxford Bulletin of Economics and Statistics, 52(2) : 169-210.
- Johansen, S., R. Mosconi et B. Nielsen (2000),« Cointegration Analysis with the Presence of StructuralBreaks in the Deterministic Trend », versionpréliminaire.
- Johansen,S. (1991), « Estimation and Hypotheses Testing ofCointegration Vectors in Gaussian Vector AutoregressiveModels », Econometrica, 59(6) : 1551-1580.
- Juselius,K. (1995), « Do Purchasing Power Parity and UncoveredInterest Rate Parity Hold in the Long Run? An Example of LikelihoodInference in a Multivariate Time-series », Journal of Econometrics, 69(1) : 211-240.
- Kurmann,A. (2006), « Monnaie, inflation et activitéréelle », Université du Quebec àMontréal, support de cours.
- Laidler, D. (1993), The Demand for Money: Theories, Evidence, and Problems, Harpers Collins college publishers New York, 224p.
- Lardic, S. et V. Mignon (2002), Économétrie des séries temporelles macroéconomiques et financières, Economica, 416 p.
- Nachega, J-C.(2001), « A Cointegration Analysis of Broad Money Demand inCameroon », IMF working paper, WP/01/26.
- Perron, P. (1997), « Further Evidence on Breaking Trend Functions in Macroeconomics Variables », Journal of Econometrics, 80(2) : 355-385.
- Pierre, M. (1964), « Notes sur la theorie monetaire de Milton friedman », Revue économique, 15(5) : 677-712.
- Plihon, D. (2001), La monnaie et ses mécanismes, La Découverte, Paris, 128 p.
- Rachline, F. (1982), « La nature de la monnaie », Revue économique, 33(3) : 446-475.
- Sriram,S. (1999), « Survey of Literature for Money: Theoretical andEmpirical Work with Special Reference to Error-correctionModels », IMF Working Paper, WP/99/64.
- Sriram, S. (2001), « A Survey of Recent Empirical Money Demand Studies », IMF staff Paper, 47(3) : 334-365.
- Stracca,L. (2001), « The Functionnal Form of the Demand for EuroArea M1 », Working Paper , 51, European Central Bank.
- Zivot, E. et D.W.K. Andrews (2002), « Futher Evidence of the Great Crash, the Oil-price Shock, and the Unit-root Hypothesis », Journal of Business and Economic Statistics, 10(1) : 251-270.
Liste des figures
Graphique 1
Évolution entre croissance monétaire et inflation en zone CEMAC
Graphique 2
Ruptures structurelles au Cameroun et au Gabon
Graphique 3
Critère de détermination du nombre optimal de partitions
Graphique 4
Ruptures structurelles en RCA et au Congo
Graphique 5
Stabilité du VECM
Graphique 6
Séries du Cameroun
Graphique 7
Séries du Gabon
Graphique 8
Séries RCA
Graphique 9
Séries du Congo
Graphique 10
Les taux d’intérêt
Liste des tableaux
Tableau 1
Test de changement structurel sur les séries camerounaises et gabonaises
Tableau 2
Test de changement structurel sur les séries centrafricaines et congolaises
Tableau 3
Résultats du test de Zivot-Andrews sur les séries camerounaises et gabonaises
Tableau 4
Résultats du test de Zivot-Andrews sur les séries centra fricaines et congolaises
Tableau 5
Vecteurs coïntégrants
Tableau 6
La matrice des poids
Tableau 7
Paramètres de court terme
Tableau 8
Test de coïntégration
Tableau 9
Test d’autocorrélation des résidus