Abstracts
Abstract
This paper examines the effects of grid compression on gender-based salary gaps. In this case, the workplace setting is a large Canadian research university previously found to have both a positionally segregated cohort of academic staff and a persistent gender-based differential in their salaries. The annual salary grids at this institution underwent seemingly subtle compressions over the course of two decades, with within-rank compression largely confined to the first decade and across-rank compression confined to the second decade.
We employ a simulation methodology to check whether the two types of compression reduce the salary gap to varying degrees. After deflating staff salaries back to the start of each decade, we project the salaries forward using the historical annual increases and grids in place in each year at the university. We compute the gap present in the salary distribution at the start and end of each decade in the simulation, and check whether the gap decreased more across one decade than the other.
We find that across-rank compression of the institution’s salary grid during the second decade narrows the salary gap to a greater extent than the within-rank compression of the earlier decade. Our work demonstrates that employers using stated salary grids could use simulation to monitor the equity effects of their pay policies and shows that they could accelerate the closure of gaps through consciously altering relationships among pay levels at different points in the grid’s hierarchy.
Keywords:
- wage equity,
- pay differential,
- simulation,
- wage determination,
- sex gender gap
Résumé
Cette étude examine les effets d’une compression de la grille salariale sur les écarts de rémunération fondés sur le genre. Le milieu de travail sélectionné est une grande université de recherche canadienne où l’on a constaté qu’il existait une cohorte de personnel ségréguée sur le plan professionnel et des différences salariales persistantes fondées sur le genre. Les grilles salariales annuelles de cette institution ont subi des compressions apparemment subtiles au cours de deux décennies, la compression intra-rangée étant largement limitée à la première décennie et la compression inter-rangée à la deuxième.
Nous utilisons une méthode de simulation afin de vérifier si les deux types de compression réduisent l’écart salarial à des degrés différents. Après avoir dégonflés les salaires du personnel au début de chaque décennie, nous les avons projetés en utilisant les augmentations annuelles historiques et les grilles mises en place annuellement à l’université. Nous avons calculé l’écart présent dans la répartition des salaires au début et à la fin de chaque décennie dans la simulation et avons vérifié si l’écart a diminué davantage au cours d’une décennie que l’autre.
Nous constatons que la compression inter-rangée de la grille des salaires de l’institution au cours de la deuxième décennie réduit l’écart salarial dans une plus grande mesure que la compression intra-rangée de la décennie précédente. Nos travaux montrent que les employeurs d’organisations et d’entreprises disposant de grilles salariales bien établies pourraient utiliser la simulation afin de surveiller les effets de leurs politiques salariales sur l’équité. Ils pourraient ainsi accélérer la réduction des écarts de rémunération entre les genres en modifiant consciemment les relations entre les niveaux de rémunération à différents points de la hiérarchie de leur grille salariale.
Mots-clés:
- équité salariale,
- écarts de rémunération,
- simulation,
- politiques salariales,
- disparités entre les sexes
Article body
Introduction
Motivation
A long line of work has documented the existence of gender-based wage and salary gaps in many markets (Jones, Makepeace and Wass, 2018; Schirle, 2015; Blau and Kahn, 2006). Such gaps are often associated with other gender-based disparities in positioning in workplaces, industries and societies (e.g., Samkharadze et al., 2015; Jacobsen, 2007). Such difference in positioning, termed gender segregation, has been described as “one of the most important and enduring aspects of labour markets around the world” (Anker, 1997: 315).
One market, for university faculty, has been the focus of considerable study, perhaps because it is an international labour market in which participants typically have high levels of education and perform similar tasks. Analyses have established the persistence of salary gaps between male and female academic employees in Canada and abroad, often pointing to gender-based segregation as a significant explanatory factor (Brower and James, 2020; Brown and Troutt, 2017; Catalyst, 2017; Carlin et al., 2013; Goastellec and Pekari, 2013; Brown, Troutt and Prentice, 2011; Takahashi and Takahashi, 2011; Warman, Woolley and Worswick, 2010). Because gender-based pay gaps have been shown to be slow to change in different kinds of organizations, there is a need for studies and policies on how to close these gaps.
The most effective but challenging method by which to decrease a gender-based salary gap may be to eliminate positional segregation, that is, to change the distribution of workers in such a way that males and females are equally represented in all ranks, positions and salaries, and then to maintain such equality until any experience premium is equally distributed by gender. However, the distribution of men and women by position and experience is slow to change in workplaces, such as universities, where careers are long. For example, if women start by disproportionately occupying lower paid positions than men, this will create a gap and slow progress towards salary equality for the duration of the cohort’s careers. Even the most conscientious efforts to change the positional distribution of men and women take time, relying on retirements after long careers with limited opportunities for hiring due to low turnover rates. This carries obvious implications for perpetuating pay gaps.
In this paper, we posit that employers can adopt a less direct method to reduce the salary gap: altering pay grids to mitigate the effect of persistent positional segregation. In particular, we compare two types of salary grid compression: compression in salary ranges within positions (and ranks) and compression in salaries across positions (and ranks). We show that, while both have a decreasing effect on the gap, the latter is more effective in the context of long careers in a workplace where women tend to have less experience and are more likely to occupy lower-paying positions than men. In light of the seeming intractability of gender-based pay gaps, our results point to a possible means of speeding their reduction through relatively small adjustments to an organization’s salary grid. As well, the simulation method we use in our analysis provides a tool, which employers can use in order to monitor gaps and the equity effects of their compensation policies.
Research setting
The employer of focus in this paper is a typical Canadian research university with a formal pay grid for its academic staff. Two findings about the university provide context for our analysis. First, gender-based positional segregation characterizes the distribution of the university’s male and female academic staff among the ranks. Despite gains in the number of female academics at the university and gains in their representation at the higher-paying ranks over time, the distribution of employees remains segregated (Brown and Troutt, 2017). Second, the university had a longstanding gender-based salary gap (Brown and Troutt, 2017; Brown, Troutt and Prentice, 2011; Haignere and Lin, 1994), which underwent a marked decrease following a period of near constancy (Brown and Troutt, 2017). Specifically, the gap in average male and female salaries was 24% in 1993, 22% in 2003, and 12% in 2013 (Brown and Troutt, 2017). These two findings, or characteristics, are common with firms and industries.
The university uses a grid structure to guide the setting and advancement of academic employees’ salaries. The university’s academic staff have been unionized since the mid-1970s, as have the academic staff of most Canadian universities. The academic salary grid at the university is regularly negotiated through collective bargaining between the university administration and the academic staff’s union. With few exceptions, each bargaining round produces a three-year agreement, with that agreement including a specific salary grid for each of the years covered.
While the general principles and logic of the salary grid have remained the same over time, some of the relationships between salaries within the grid display two distinct periods of adjustment, each approximately a decade long. These periods of contrasting grid adjustment form the basis of our study. Across one decade, within-rank compression of the grid occurred, shrinking the range between each rank’s minimum and maximum salaries. In the next decade, the grid underwent across-rank compression, decreasing the ratio of the highest- to lowest-paid ranks’ salaries. Whether these compressions were purposeful and, if so, in pursuit of what goal are uncertain. Despite general concern with respect to the gender salary gap, neither the union nor the university made any public pronouncements to indicate that either period of compression was explicitly aimed at reducing the gap. However, since women at the institution tend to be at the lower end of some ranks’ salary range and overrepresented in lower-paying ranks, when we noticed the distinct types of compression, their effects on the salary gap seemed worthy of examination.
Contribution to theory and practice of salary determination
This paper makes a unique contribution to the discussion of salary determination through both the focus of its inquiry, comparing the effects of specific types of grid compression on the gender salary gap, and through its method of analysis, simulation. While our study uses data from a university, its methodology applies generally to organizations with a defined salary grid.
Our work provides an innovative approach to the current understanding of pay inequality. Most work to date attempts to explain various dimensions of the pay gap (Blau and Kahn, 2017; Heinz and Wolf, 2010), identifying the role of salary structure, collective bargaining and various characteristics of firms and workers in affecting the gender gap. In Canada, the Canadian Association of University Teachers (2011: 7) identified pay practices as a possible contributor to the persistent pay gaps found in Canadian academia, stating, “[w]omen may…be disadvantaged by the traditional academic salary grid system” and pointing to the “need to assess how current … salary grid systems may be contributing to the gender pay gap.” Recent work also examines the weakness of traditional explanations in explaining the academic gender salary gap (Brower and James, 2020), noting that research output and age explain less than 50% of the current gap. However, while the underlying causes of gender gaps are debated, few studies propose and road test tools to reduce these gaps. Our study provides and defends a strategy for reducing pay gaps through across-rank compression and demonstrates a forecasting method, which any organization with a set pay grid could use to consider the equity effects of its pay practices, including anticipated changes to its pay practices.
Research on pay gaps commonly theorizes that formalized pay policies limiting discretion benefit marginalized groups such as female employees and may play a role in narrowing or preventing inequitable pay gaps (Kessler and Pendakur, 2015; Doucet, Smith and Durand, 2012; Canadian Association of University Teachers, 2011; Elvira and Saporta, 2001). With respect to Canadian universities, Warman, Woolley and Worswick (2010) found that larger pay gaps existed at Canadian academic institutions where pay increases were based on more subjective judgements of an employee’s merit. Doucet, Smith and Durand (2012) found pronounced gender-based disparities in more discretionary processes such as promotion and pay supplementation, while they found no significant gender-based difference in base salaries, which were determined through a highly transparent, formalized grid system. Bakker et al. (2010:9) also point to the potential contribution of any “discretionary component” to the emergence, persistence, or widening of a gender salary gap at a Canadian university. Our study supports the finding that a formal salary grid can be a useful tool to temper a gender-based salary gap.
Like other researchers studying gender salary gaps (e.g., Brower and James, 2020; Blau and Kahn, 2017), we have found that the pace of improvement toward salary equity is painfully slow, with positional segregation a contributing factor (Brown and Troutt, 2017). Brower and James (2020) find evidence that the segregation and gender pay gap in New Zealand’s academic sector will not diminish through attrition of long-serving senior men, as is commonly speculated. Our university’s use of a formal salary structure should limit the creation of gender-based salary differences. However, it does not correct gaps created by historical practices or unconscious biases, such as segregated hiring and promotion rates. This is because, aside from time of hire and promotion in rank, an academic’s annual salary at the university is determined almost entirely by increases that depend on where their salary falls within the grid structure. Therefore, without concrete intervention, the grid structure can perpetuate gaps formed by the commonly persistent segregation of employees within it.
Given the importance of formalized pay structures and practices in reducing gender pay gaps, the university’s grid serves as an excellent jumping off point to examine how salary compression can be used to reduce gaps. The periods of contrasting types of grid compression provide a chance to test the effect of each in turn on the institution’s gender salary gap. In this paper, we use simulation methodology to explore the effect of each period of grid compression on the gap. By applying the changing salary grid to a common cohort of employees with a fixed positional distribution, we show how the two types of compression reduce the gap to differing extents. Such a use of salary simulation illustrates how workplaces could target salary compression to reduce gender pay gaps.
It is important to recognize both the strengths and weaknesses associated with compression of salaries. Bellas, Ritchey and Parmer (2001) express concern about the degree to which market forces have compressed salaries in academia, even while recognizing compression’s role in decreasing the gender salary gap. They speculate that the relatively faster growth they observed in female faculty salaries at a United States university could result from women’s greater likelihood of being more recently hired. Women’s (starting) salaries reflected increases due to market forces, while the salaries of men with long tenures had stagnated due to institutional and government practices limiting annual increases. At another U.S. university, Hampton et al. (2000) found that similarly driven salary compression was sufficiently pronounced to offset the factors that would lead to a gender-based salary gap. More widely, Harmon et al. (2018) report that, as of the 2017-18 year, 99 out of 892 American post-secondary institutions in their analysis also exhibited such compression. At 22 of those, average (entry-level ranking) assistant professor salaries exceeded average (mid-ranking) associate professor salaries, representing salary inversion (Harmon et al., 2018).
Business management and human resources experts caution that a high degree of salary compression may lead to low employee morale and reduced employee productivity (e.g., ERI Economic Research Institute, 2017). However, the degree of grid compression that we highlight in this paper helps to narrow gender-based salary gaps and is sufficiently mild to avoid these negative effects. Furthermore, compression within a grid plays a different role than compression imposed by the market. In the former case, the progression of salaries through the ranks continues to follow an upward trajectory. In the latter, compression is the result of starting salaries that are well above the minimum starting salary at the lowest rank, and, in the case of inversion, as Harmon et al. (2018) note, above the mean salary of higher ranks.
The compression we examine in this study is applicable well beyond the university sector. It is “consistent with international evidence that unions compress the distribution of wages of their members by securing relatively higher premiums” for employees at the lower-end range of the pay grid (Casale and Posel, 2010: 31). Similarly, Edin and Richardson (2002) attribute the substantial decrease in Sweden’s gender pay gap from the 1960s through the early 1980s to the compression achieved in the country’s overall wage structure during that same period. A women’s activist group of the United Steelworkers, Women of Steel (2017: 7) also advocates grid compression as a solution to pay inequity in workplaces where “women are concentrated in the lower end of the grid.” Furthermore, Schäfer and Gottschall (2015: 491) assert, “there is still room for [measures such as]…pay raises in low-paid and female-dominated sectors or gender-sensitive monitoring of pay dynamics.”
The salary compression at the university has taken place in a unionized environment where collective bargaining determines pay practices for each year. However, we would argue that unionization is not essential to our methods and results.
Unionization itself has yielded mixed results with respect to its effect on equity, including on gender-based wage and earnings gaps. The collectively bargained policies and practices in unionized workplaces tend to reduce the potential for individualized, arbitrary, discretionary and/or opaque or otherwise hidden decisions concerning an employee’s pay (Elvira and Saporta, 2001; Sosin, Rives and West, 1998), thereby providing the context for harnessing the benefits provided by a formalized remuneration structure in reducing the gender salary gap. Elvira and Saporta (2001) find unionization to be associated with lower gender-based wage gaps in a wide swath of the U.S. manufacturing sector. Casale and Posel (2010: 30) also point to the “inequality-reducing effect” commonly found in empirical studies on the effects of unionization in the South African workforce. With respect to academia, Sosin, Rives and West (1998: 28) state, “[s]tudies of the impact of unions in American higher education conclude that the positive impact on salaries is, at best, relatively small, unlike the positive effect found in the industrial relations literature.”
The present work builds on previous research on the gender salary gap. We recognize that the gap exists, that its causes are a matter of debate, and that the gap in academia and other stratified workplaces is not expected to close in the foreseeable future, despite unionization and the existence of a formalized pay structure. We contribute to existing knowledge of the gender pay gap by using a simulation method to project salaries through an evolving grid to see the effects on the university’s salary gap over time. Our method enables a direct comparison of the effects of two dimensions of grid compression on the gender salary gap in an organization with a clearly defined salary grid. This provides a tool that employers using a pay grid can use to forecast the equity effects of their pay practices and policies. Our results show that a small amount of compression across ranks is more effective than within-rank compression to reduce a persistent gender pay gap.
Salary grid and annual salary increases
Salary grid
Academic staff at the university hold either a teaching-focused position or a research-focused position. There are three ranks within each of these positions, for a total of six ranks. Employees ascend through the ranks within their position, only rarely moving from one position to the other. Employees holding teaching-focused positions occupy ranks 1 through 3 of the annual salary grid, while those holding research-focused positions occupy ranks 4 through 6. Ranks 1 and 6 of the grid are, respectively, the lowest and highest paid.
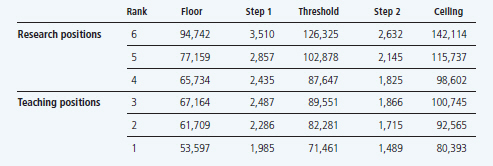
The salary grid defines key parameters for employees’ salaries at each rank and plays a central role in determining an employee’s annual pay increase. A sample salary grid[1] in Table 1 represents the historic annual grids we used in this study. It is noteworthy that the structure and logic of the grid have not changed.
Table 1
Sample salary grid ($)
For each rank, the grid specifies a binding floor and a soft ceiling. No employee new to a rank may be paid a salary lower than that rank’s floor. However, an employee may receive a salary above the ceiling for their rank as a result of the annual salary increase process described below. The grid also specifies a threshold salary and steps 1 and 2 for each rank. The threshold salary is used to determine which step the employee will receive in the annual salary increase process. Steps 1 and 2 are lump sum amounts that are normally added to an employee’s salary during the annual salary increase process. Step 1 exceeds step 2, and both steps’ values increase with rank through the teaching and research positions. All five of these parameters are determined through bargaining.
Salary increase process
Each year, each employee’s current salary undergoes an increase based on a combination of three determinants: the overall salary increase for the new salary year; the step payment policy for the new salary year; and, the employee’s current salary compared to the floor, threshold and ceiling for their rank (which may be a new rank if they were promoted during the current salary year). These three determinants are products of collective bargaining.
The actual overall salary increases and step payment policies negotiated at the university over the course of the study period appear in Table 2. A given year’s overall salary increase may be a percentage or lump sum amount, though it is typically a percentage. It can also vary by rank, although it is usually the same for all ranks. Typically, a given year’s step payment policy is to pay the step amount specified in the salary grid. However, as seen in Table 2, some years’ step payment policies have deviated from that typical approach. We discuss the salary increases and step payment policies below.
Table 2
Overall salary increases and step payment policies by year
* S teps paid only to employees whose current year salary was less than threshold for their rank; step amounts were $1,000 (ranks 6 and 3), $1,500 (ranks 5 and 2) and $2,000 (ranks 4 and 1).
** L ump sum increases of $0 (ranks 6 and 3), $1,500 (rank 5) and $900 (ranks 1, 2, and 4) were first applied to current year salary, with a 2.9% increase then applied to the result.
he left-hand column has two shadings. The top shading shows years when increases were negotiated under a rightleaning government. The bottom shading shows years when increases were negotiated under a left-leaning government.
The annual process of increasing each employee’s salary follows a series of actions using the three determinants listed above. First, the overall salary increase for the new year is applied to each employee’s current salary (regardless of whether their current salary exceeds their rank’s ceiling). Next, a step payment is added according to the step payment policy in place for the new salary year. If a step is to be paid, an employee’s eligibility to receive the payment is determined by comparing their current year salary (prior to the overall increase) to the threshold and ceiling salaries stated in the new year’s grid for their continuing or newly-attained rank. If an employee’s current year salary falls below the threshold in the new grid, they receive the higher step 1. If their salary falls at or above the threshold but below the ceiling in the new grid, they receive the lower step 2. If their current salary has reached or surpassed the new grid’s ceiling for their rank, they are not eligible to receive that year’s step payment. The final step of the salary increase process is a check that each employee’s salary is at least at the floor for their rank in the new grid, bumping any salaries up to the floor if needed. Depending on the specifics of the three determinants used in this process, it is possible for a particular employee, or even all employees, to receive a zero increase in a particular year.
To illustrate the salary increase process, imagine an employee currently earning $110,000 who was promoted from rank 5 to 6 during the current year. Imagine too that, in the new year, a 1% overall salary increase and the steps listed in the new year’s grid are to be paid, and that the new grid is the sample grid shown in Table 1. According to the annual salary increase process, this employee’s new salary will be determined as follows. First, the 1% overall salary increase is applied. This brings the employee’s salary to $111,100. Second, a step payment is added to the employee’s salary. The amount of the step payment is determined by comparing the employee’s current salary of $110,000 to the threshold salary stated in the new grid for the employee’s new rank (rank 6). Since the employee’s current salary of $110,000 is less than rank 6’s threshold of $126,325, the employee receives rank 6’s step 1 payment of $3,510, bringing their new salary to $114,610. Lastly, because this employee received a promotion in the current year, their new salary of $114,610 is checked to ensure that it is at least at the floor level for their new rank. In this case, it is, so no further adjustment is made.
The salary grid, and changes to it, can critically influence an employee’s salary trajectory. This is because each employee’s salary moves according to salary levels in the grid, which themselves may move, or not, across time periods, as well as to relationships among those levels which have undergone changes as the grid has evolved.
Grid evolution
This study examines how the grid has changed across a period of 24 years, and the implications of the changes for the gender salary gap at the university. In particular, we identify two different types of grid compression that took place over this time. During roughly the first decade, the grid underwent within-rank compression, while it underwent across-rank compression during roughly the following decade.
Figure 1 charts ratios of key salary levels in the grid annually, within and across ranks. For example, the top line shows that, in year 1, rank 6’s floor and ceiling salaries were each 2.2 times rank 1’s corresponding salaries. Similarly, the lowest line shows that, in year 1, each rank’s threshold was 1.7 times its floor.
Figure 1
Relationships in the salary grid over time
Figure 1 shows that within-rank compression of the grid occurred during roughly the first decade of our analysis. The solid line in Figure 1 depicts the ceiling-to-floor ratio for a representative rank (rank 6). In Figure 1, we see this line drop midway through the first decade and then level off across the second decade. Specifically, this ratio started at 1.7, rose to 1.8 in year 4, then fell to 1.5 by year 6, where it remained through year 24. This drop shows that the range from each rank’s floor to its ceiling shrank, or underwent compression, midway through the first decade. This within-rank compression resulted primarily from a relatively greater nominal increase in the ranks’ floors than in their thresholds and ceilings during this period. The increase in the ranks’ floors was almost 80% greater than the increase in their thresholds and ceilings.
In contrast, across-rank compression is evident only in the second decade, as shown in the upper (patterned) set of lines in Figure 1. Each of these lines charts the ratio of a rank 6 to rank 1 salary parameter. The dashed line represents the ceiling ratios. It illustrates that the ratio of rank 6’s ceiling to rank 1’s was constant at 2.2 during years 1 through 14, then fell to 1.9 in year 15 and to 1.8 in year 18. The diamond line represents the ratio of rank 6 to rank 1 floors. It shows that the compression of salary floors between ranks was slightly greater than that of salary ceilings. This was due to increases in the floors at the lowest ranks.
Evolution of overall salary increases and step payment policies
While the general expectation for salary increase is that a percentage overall increase and step payment are both awarded each year, there was variation over time, as shown in Table 2. Overall salary increases have been awarded as percentages in most years. However, they were paid as lump sum amounts in three years and as a combination of percentage and lump sum amounts in four years, and were not awarded during another four years. The usual steps were paid in 20 years of the study horizon. In years 4 and 5, they were withheld along with overall salary increases, and in years 6 and 7, they were only paid to employees whose salaries were below the threshold salary for their rank (those eligible to receive the higher step 1). Furthermore, the amounts paid were inverted by rank, with lower-ranked eligible employees receiving larger steps than higher-paid eligible employees do. The austerity that marks the variation from the norm in the earlier decade offsets the high overall increases to salaries paid in the first three years.
Employee data and simulation methodology
Data
In addition to the annual salary grids, overall pay increases and step payment policies for 24 years, the data for this study include administrative salary data for the full cohort of academic staff at the university in year 24. By year 24, the institution had both hired and promoted a significant number of women. This means the simulations using this cohort should generate the most conservative results in terms of gap reduction effect from salary grid changes. The variables we use from the administrative salary data are gender, real full-time salary net of stipends[2] and rank.
Table 3 shows the rank distributions for men and women in the cohort of employees.
Table 3
Distribution of year 24 employee cohort* across ranks
For this cohort, the majority of the university’s academic staff hold research-focused positions; only 17% of the staff work in teaching-focused positions. Women comprise only 36% of the research-focused positions but 61% of the teaching-focused positions. Women are significantly less likely than men to hold the highest paid rank. A woman had an 18.6% probability of holding rank 6, while a man had a 38.7% likelihood of holding this rank (Brown and Troutt, 2017).
Simulation
Our analysis simulates the annual movement of the year 24 cohort’s salaries over two consecutive decade-long horizons using the salary grid, overall pay increase and step payment policy in effect in each year. The purpose of the simulation is to examine whether the different decades’ respective grid compressions produce different projected effects on the gender-based salary gap.
To perform this analysis, we first deflate the cohort’s actual year 24 salaries to the start year for each decade. We compute the gender-based salary gap in each decade’s start year (deflated) salaries for comparison purposes. We then project each employee’s start year salary forward annually for 10 years by applying the overall salary increases and step payment policies within the year’s salary grid. This yields projected salaries at the end of each decade of the simulation, when we again compute the gender-based salary gap. Comparing the starting and ending salary gaps in each decade allows us to check which decade experienced the greatest decrease in the simulated gap. Although simple to execute, this simulation required a series of decisions.
First, since we needed to apply two decades worth of nominal annual salary increases and grids to the cohort’s salaries, we had to determine a process to convert salaries, or grids’ salary parameters and overall increases, to like terms. This necessitated both choosing whether to deflate salaries versus salary increases and grids, and choosing a deflator. We chose to deflate the salaries to each simulation start year rather than deflate grid parameters and salary increases because deflating fewer items would introduce less error to the simulation.
Second, we sought a deflation method that, as much as possible, ensured that the cohort’s deflated salaries fit the salary grid in place in each simulation decade’s respective start year. Ideally, the deflation method would also produce similar salary gaps at the start of each decade to provide a clear starting point for the simulation.
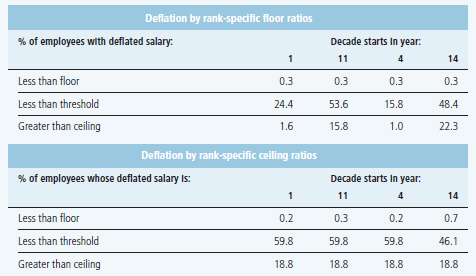
Because the salary data fit the internal structure of the year 24 grid, which is markedly different from the grids in place 20 or even 10 years earlier, a simple GDP deflator or consumer price deflator was not sufficient to achieve a good fit between the deflated salaries and the starting year grids. Indeed, applying a single common deflator to all salaries led to start year salaries that were unworkable, with a large proportion of salaries below floors or above ceilings. This suggested we needed to use rank-specific deflators based on the salary grids. We deflated the salaries to their decade start years using rank-specific ratios of floors from the grids. For example, to deflate a rank 4 salary to year 4, we multiplied it by 0.5056, which is the ratio of rank 4’s floor salaries of $31,393.80 and $62,091 in, respectively, years 4 and 24. This resulted in a distribution of starting salaries with similar salary gaps in the base year for each decade that also fit the starting salary grid for the simulation. As a robustness check, we also ran the simulation using comparable ceiling deflators.
Third, we needed to choose start years for the decades in the simulation from among our 24 years of data on the university’s salary increase process. Given our observations about the changes in the grids, overall salary increases and step payment policies, as well as the political changes in our province, testing the sensitivity of our results to the specific simulation start year also seemed warranted as a further robustness check. Therefore, we ran the simulation over two different choices of decades for analysis. The first compared the decades spanning years 1 through 11 and 11 through 21; the second compared the decades spanning years 4 through 14 and 14 through 24.
Table 4 describes the fit between deflated salaries and starting year grids for our simulation and robustness checks, according to choices of deflation factor and definition of decades. Both deflation method and decade definition inevitably produce variation in salary distributions for a simulation. The proportions of employees whose salaries exceed the threshold or ceiling for their rank differ based on the choices made. For example, using floor ratios to deflate the year 24 salaries back to year 1 rather than year 4 to start a simulation means that 24.4% rather than 15.8% of employees in the simulation begin the first decade with salaries above threshold for their rank, meaning they are eligible to receive the lower step 2. This means that differing portions of the cohort will experience particular salary increase trajectories over the decade, which could have implications for the closure of the simulated gap. In light of this, when we present our results in the next section, we show the gap reduction outcomes for both choices of deflation factors applied to both sets of simulation decades.
Table 4
Distribution of year 24 deflated salaries resulting from choices of deflation factor and decade start year
Finally, we needed to make decisions about the cohort’s career progression over time. Men and women enter, leave and retire from the institution at differing rates, and men and women at rank 5 experience differing rates of promotion to rank 6, which is consistent with the empirical literature in this area (Brown and Troutt, 2017). However, introducing hiring, promotions through ranks and departures to the simulation would necessitate assumptions that would likely blur the effects of the grid compressions. Therefore, in order to highlight the effects of the grid, we chose not to advance employees through the ranks and not to have any of the cohort retire or otherwise exit the simulation. That is, in the simulations presented, all members of the cohort remain in the cohort holding their rank throughout the two separate decades of their salary projection.
Results and discussion
Table 5 presents our results for four simulation scenarios representing different combinations of choice of deflator (floor ratios vs ceiling ratios) and definition of decades (years 1-11 and 11-21 versus 4-14 and 14-24).
Table 5
Summary of changes in the gender-based salary gap across simulations for scenarios varying by deflator and decade start year
The gender-based gap in the deflated salaries at the start of each decade is virtually the same across all scenarios, at 14.6% or 14.7%. This consistency across simulation scenarios means that we are estimating the reduction in the gap across decades from a common baseline.
The results in Table 5 show that the across-rank compression of the salary grid during the second half of our study horizon has a greater impact than the earlier within-rank compression in terms of reducing the gender-based salary gap. In all four scenarios, both decades’ salary increases and grid movements yield a notable reduction in the salary gap. However, the decade 2 changes yield a considerably larger reduction, ranging from 1.4 to 2.3 times that of the decade 1 reduction, depending on the scenario. The most conservative scenario exhibits the smallest difference in gap reduction between decades of analysis. It is the scenario in which the year 24 salaries are deflated to years 1 and 11 using floor ratios. Figure 2 shows the progression of simulated salaries for each decade in this scenario. Both lines in Figure 2 start at the same base-year gap, but the line for decade 2 falls at a steeper slope to reach a smaller gap by year 10 of the simulation. The scenario that produces the largest relative gap reduction in decade 2 versus decade 1 is that in which we deflate the cohort’s salaries by ceiling ratios to years 4 and 14. The three other scenarios look similar to Figure 2, with slightly different slopes for each scenario.
Figure 2
Simulated gap (%) for the scenario with floor deflators and decades starting in years 1 and 11
To further check the influence of the deflation method, we checked whether the proportions of men and women whose salaries are at or above the ceiling in the base year affected our results. From Table 5, we see that these proportions differ widely across scenarios. However, there is a consistent result that the first decade’s grid changes produce a smaller reduction in the salary gap than the second decade’s reduction. This result is robust to choices of specific definitions of decade of analysis and choice of deflation factor.
Conclusion
This paper contributes to knowledge about gender-based salary gaps and salary compression by using simulation methodology to examine the effects of two different dimensions of salary compression on the gender salary gap at a Canadian university. Specifically, we detailed historic shifts in the university’s salary grid over a 24-year period, noting that the grid experienced within-rank compression during the earlier half of that horizon and across-rank compression during the latter half of that horizon. We then used simulation methodology to project salaries across consecutive decades of that horizon using the pay increase policies and salary grids in place in each year. We found that, for a cohort of employees where women are more likely to hold lower-paying positions and ranks, across-rank compression of the salary grid served to reduce the gender-based salary gap to a greater extent than within-rank compression of the grid. This result is robust to technical decisions for the simulation methodology, such as specific definitions of decade of analysis and choice of deflation factor.
In contrast to much of the current literature on gender salary gaps, we have focused not on possible causes, but on tools that employers and, where applicable, unions could use to reduce an existing gap. These tools are simulations to project the equity effects of workplace pay policies and practices (or changes to them), and across-rank salary grid compression. Both the simulation method we use in our analysis and our findings about grid compression are potentially relevant to other public and private sector workplaces.
First, the simulation method we use in this analysis can be adopted by employers to improve salary equity. By projecting salaries forward, an employer or union can determine whether current policies will lower an inequitable gap, leave it untouched, or widen it over time. Employers could also use the simulation method demonstrated here to analyze the effects on their salary gap when any new payment policy is being considered. More broadly, simulations could examine salary gaps affecting other groups, such as racialized employees, indigenous employees and persons with disabilities.
Second, our findings show that seemingly subtle compression of a salary grid plays a role in reducing gender-based pay gaps, thereby forming the basis of a strategy that workplace managers can use to accelerate the closure of gender pay gaps. Purposeful compression, chosen through simulation analysis, can reduce a salary gap while avoiding the pitfall of unplanned market-driven compression previously studied. If an employer has a formal pay grid and its employees differ by position and experience across genders, it could strategically compress salaries across ranks or positions. This strategy can reduce a seemingly intractable gap more quickly than positional readjustments which research has found to be often slow in coming. This strategy is applicable to any public or private sector workplace committed to closing inequitable pay gaps. Importantly, this type of beneficial compression need not rely on unionization.
Future work in this area could answer questions about the effects of other variables and behaviours on the salary gap. We could construct scenarios with varying rates at which employees enter and exit the workplace as well as advance through the hierarchy of ranks in an organization’s salary grid. In this case, the assumptions made regarding men’s and women’s rates of entry, exit and career progression through the hierarchy—all of which are aspects of employment susceptible to systemic discrimination—could be chosen and varied to examine their effects on the gender-based pay gap. In addition, where data exist, research could extend this work beyond gender to include other groups who are at risk of discrimination.
Appendices
Notes
-
[1]
The (university’s actual) structure presented here is fairly simple, including only two positions with three ranks each. The analysis could be applied to a different setting or even a structure with more classifications. For example, a shipping company might have three positions with internal ranks: a set of clerical ranks, a separate set of ranks for persons working in the warehouse, and a set of driver ranks.
-
[2]
Stipends are additional annual lump sum amounts paid to employees while they perform temporary functions in addition to their regular duties. We exclude stipends, as they form no part of the institution’s salary increase process.
Appendices
Acknowledgements
This paper benefitted greatly from the insightful feedback we received from Dr. Anthony Morven Gould and two anonymous reviewers. We also thank participants at the 10th Biennial International Interdisciplinary Conference on Gender, Work & Organization and participants at the 53rd Annual Canadian Economics Association Meetings for their input on earlier drafts of the paper.
References
- Anker, Richard (1997) “Theories of Occupational Segregation by Sex: An Overview.” International Labour Review, 136 (3), 315-339.
- Brown, Laura K. and Elizabeth Troutt (2017) “Sex and Salaries at a Canadian University: The Song Remains the Same or the Times They are a Changing’?” Canadian Public Policy, 43 (3), 246-260.
- Brown, Laura K., Elizabeth Troutt and Susan Prentice (2011) “Ten Years After: Sex and Salaries at a Canadian University.” Canadian Public Policy, 37 (2), 239-255.
- Bakker, Karen, Lara Boyd, Nicole Fortin, Jim Johnson, Mark Trowell and Walter Sudmant (2010) An Analysis of the Gender Pay Gap in Professorial Salaries at UBC: Report of the Pay Equity (Data). Working Group. The University of British Columbia.
- Bellas, Marcia L., P. Neal Ritchey and Penelope Parmer (2001) “Gender Differences in the Salaries and Salary Growth Rates of University Faculty: An Exploratory Study.” Sociological Perspectives, 44 (2), 163-187.
- Blau, Francine D. and Lawrence M. Kahn (2017) “The Gender Wage Gap: Extent, Trends, and Explanations.” Journal of Economic Literature, 55 (3), 789-865.
- Blau, Francine D. and Lawrence M. Kahn (2006) “The U.S. Gender Pay Gap in the 1990s: Slowing Convergence.” International Labor Review, 60 (1), 45-66.
- Brower, Ann and Alex James (2020) “Research Performance and Age Explain less than Half of the Gender Pay Gap in New Zealand Universities.” PLoS ONE, 15 (1), e0226392. Retreived from: https://doi.org/10.1371/journal.pone.0226392.
- Canadian Association of University Teachers (2011) The Persistent Gap: Understanding Male-Female Salary Differentials amongst Canadian Academic Staff. CAUT Equity Review No. 5. March 2011.
- Carlin, Paul S., Michael P. Kidd, Patrick M. Rooney and Brian Denton (2013) “Academic Wage Structure by Gender: The Roles of Peer Review, Performance and Market Forces.” Southern Economic Journal, 80 (1), 127-146.
- Casale, Daniela and Dorrit Posel (2010) “Unions and the Gender Wage Gap in South Africa.” Journal of African Economies, 20 (1), 27-59.
- Catalyst (2017) Quick Take: Women in Academia. Retrieved from: https://www.catalyst.org/research/women-in-academia, (August 28, 2015).
- Doucet, Christine, Michael R. Smith and Claire Durand (2012) “Pay Structure, Female Representation and the Gender Pay Gap among University Professors.” Relations industrielles/Industrial Relations, 67 (1), 51-75.
- Edin, Per-Anders and Katarina Richardson (2002) “Swimming with the Tide: Solidary Wage Policy and the Gender Earnings Gap.” Scandinavian Journal of Economics, 104 (1), 49-67.
- Elvira, Marta M. and Ishak Saporta (2001) “How Does Collective Bargaining Affect the Gender Pay Gap?” Work and Occupations, 28 (4), 469-490.
- ERI Economic Research Institute (2017) How to Manage Salary Compression Issues. Irvine, California USA, ERI Economic Research Institute. November 2017. Retrieved from: https://downloads.erieri.com/pdf/How_to_Manage_Salary_Compression.pdf, (July 23, 2019).
- Goastellec, Gaele and Nicolas Pekari (2013) “Gender Differences and Inequalities in Academia: Findings in Europe.” In Ulrich Teichler and Ester Höhle (eds.), The Work Situation of the Academic Profession in Europe: Findings of a Survey in Twelve Countries. Dordrecht: Springer Science+Business Media, p. 55-78.
- Haignere, Lois and Yangjing Lin (1994) Report of the Analysis of Systemic Gender Differences in Academic Salaries at the University of Manitoba. Albany, NY: United University Professions.
- Hampton, Mary, Carol Oyster, Leticia Pena, Pamela Rodgers and John Tillman (2000) “Gender Inequity in Faculty Pay.” Compensation and Benefits Review, 32 (6), 54-59.
- Harmon, Oskar, Barbara Hopkins, Robert Kelchen, Joe Persky and Joseph Roy (2018) The Annual Report on the Economic Status of the Profession, 2017-18. American Association of University Professors (AAUP). March-April 2018. Retrieved from: https://www.aaup.org/report/annual-report-economic-status-profession-2017-18, (May 6, 2019).
- Jacobsen, Joyce P. (2007) The Economics of Gender. (3rd edition), Malden, MA: Blackwell.
- Jones, Melanie, Gerry Makepeace and Victoria Wass (2018) “The UK Gender Pay Gap, 1997-2015: What is the Role of the Public Sector?” Industrial Relations, 57 (2), 296-319.
- Kessler, Anke S. and Krishna Pendakur (2015) Gender Disparity in Faculty Salaries at Simon Fraser University. July 10, 2015. Retrieved from: https://www.sfufa.ca/wp-content/uploads/2015/07/salary_equity_study.pdf, (July 23, 2019).
- Samkharadze, Sopio, Zurab Alkhanishvili, Landa Lursmanashvili and Nino Gvasalia (2015) “Gender Stereotypes and Labour Segregation in Dental Offices.” European Scientific Journal, SE (2), 307-313.
- Schäfer, Andrea and Karin Gottschall (2015) “From Wage Regulation to Wage Gap: How Wage-Setting Institutions and Structures Shape the Gender Wage Gap Across Three Industries in 24 European Countries and Germany.” Cambridge Journal of Economics, 39 (2), 467-496.
- Schirle, Tammy (2015) “The Gender Wage Gap in the Canadian Provinces, 1997-2014.” Canadian Public Policy, 41 (4), 309-319.
- Sosin, Kim, Janet Rives and Janet West (1998) “Unions and Gender Pay Equity in Academe: A Study of U.S. Institutions.” Feminist Economics, 4 (2), 25-45.
- Takahashi, Ana Maria and Shingo Takahashi (2011) “Gender Salary Differences in Economics Departments in Japan.” Economics of Education Review, 30 (6), 1306-1319.
- Warman, Casey, Frances Woolley and Christopher Worswick (2010) “The Evolution of Male-Female Earnings Differentials in Canadian Universities, 1970-2001.” Canadian Journal of Economics, 43 (1), 347-372.
- Women of Steel (2017) Closing the Gender Wage Gap: We Can Do It Through Bargaining. Toronto: Research Department, United Steelworkers Canadian National Office. Retrieved from: https://www.usw.ca/act/activism/women-of-steel/resources/body/gender_wage2019-EN.pdf, (July 23, 2019).
List of figures
Figure 1
Relationships in the salary grid over time
Figure 2
Simulated gap (%) for the scenario with floor deflators and decades starting in years 1 and 11
List of tables
Table 1
Sample salary grid ($)
Table 2
Overall salary increases and step payment policies by year
* S teps paid only to employees whose current year salary was less than threshold for their rank; step amounts were $1,000 (ranks 6 and 3), $1,500 (ranks 5 and 2) and $2,000 (ranks 4 and 1).
** L ump sum increases of $0 (ranks 6 and 3), $1,500 (rank 5) and $900 (ranks 1, 2, and 4) were first applied to current year salary, with a 2.9% increase then applied to the result.
he left-hand column has two shadings. The top shading shows years when increases were negotiated under a rightleaning government. The bottom shading shows years when increases were negotiated under a left-leaning government.
Table 3
Distribution of year 24 employee cohort* across ranks
Table 4
Distribution of year 24 deflated salaries resulting from choices of deflation factor and decade start year
Table 5
Summary of changes in the gender-based salary gap across simulations for scenarios varying by deflator and decade start year







 10.7202/1008195ar
10.7202/1008195ar