Corps de l’article

Introduction

La comparaison de séquences d’enseignement des mathématiques dans des classes ordinaires et d’adaptation scolaire a permis de mettre en évidence que ces milieux se différencient par le temps consacré publiquement au traitement des erreurs (René de Cotret et Giroux, 2003). Ainsi, en classe ordinaire, les échecs non résolus après une nouvelle explication de l’enseignante seraient rapidement renvoyés dans la sphère privée de l’élève alors qu’en classe d’enseignement spécialisé, l’échec resterait constamment à la surface de l’échange didactique jusqu’à ce que l’enseignante l’estime résorbé ou encore qu’il renonce à obtenir le comportement qui lui paraît révélateur du savoir visé (Favre, 1997).

Nous nous proposons, dans cet article, d’analyser les interactions didactiques langagières centrées sur le repérage et le traitement de l’erreur de manière à circonscrire, dans l’institution de l’enseignement spécialisé, les stratégies que s’autorisent les acteurs du système didactique aux prises avec l’ignorance. Nous nous appuyons sur des extraits de situations ordinaires d’enseignement-apprentissage observées dans des classes d’adaptation scolaire. Deux de ces extraits proviennent d’une séquence de trois semaines d’observations « naturalistes » d’une classe d’élèves de 7 à 10 ans, en difficulté d’apprentissage, alors que le troisième est tiré d’observations similaires dans une classe d’élèves de 6 et 7 ans présentant des troubles de langage. Ces extraits ne présentent pas de caractéristiques particulières ou exceptionnelles au regard de l’ensemble des protocoles dont nous disposons. Ils ont été choisis en raison des échanges verbaux auxquels ont donné lieu le repérage d’erreurs ou de difficultés et pour les cas de figures différents qu’ils permettent de traiter : 1) le traitement ponctuel de l’erreur en séance de correction ; 2) le traitement d’erreurs repérées lors de la réalisation d’une fiche mathématique.

Le texte est construit à l’image d’une charnière dont l’une des lames est composée des extraits de protocoles de classe et la seconde, d’un questionnement théorique sur la spécificité des échanges verbaux dans les classes de l’enseignement spécialisé. Les analyses engagées sur les protocoles visent à dégager la signification des interactions didactiques par le biais de ce qu’elles provoquent comme actions chez l’un ou l’autre des protagonistes. Les actes langagiers sont considérés d’un point de vue pragmatique comme une action particulière dans un contexte et faisant appel à un contenu qu’est la connaissance. Considérant la classe comme un lieu particulier de production de significations, cette position cherche à s’inspirer du processus sémiotique de Peirce selon lequel décrire la « signification d’un signe c’est décrire le processus cognitif par lequel le signe est interprété et provoque un type d’action » (Everaert-Desmedt, 1990, p. 29). L’interprétation du signe ne se réduit pas, dans ce contexte, à déterminer « un agir d’ordre ponctuel » mais sert aussi à provoquer une « action conçue » (Fisette, 1996) faisant appel ainsi à la pensée.

La recherche d’une prise de contrôle à travers les interactions didactiques

Pour cadrer nos analyses, nous partons d’un schéma de Brousseau (1988) qui, considérant un échec de l’enseignement, présente des phénomènes didactiques relatifs à l’évanouissement du sens des connaissances et susceptibles de se manifester dans la négociation du contrat. Des négociations différentes du contrat sont déclinées selon que l’échec est ou non reconnu ou non par l’enseignante. Ce schéma est directement suivi d’un second schéma qui porte sur les différents rôles du maître et de l’élève. Le premier schéma est peu connu, bien que les phénomènes auxquels il réfère, décrits dans la théorie des situations didactiques, soient largement diffusés. Le second, toutefois, est devenu un classique puisqu’il est à la source d’un champ fécond de recherche de la didactique des mathématiques, soit celui de la structuration des milieux (Margolinas, 1997 ; Bloch, 1999).

Nous pourrions supposer que le premier schéma est une vue grossissante d’une pièce du second schéma, P2 (« professeur enseignant agit sur ou observe »). Qui est le sujet P2 ? « C’est le professeur qui enseigne, il est dans la situation didactique, il agit et il a devant lui quelque chose qui est la solution d’apprentissage, et il a à côté de lui, indépendamment de la situation d’apprentissage, un élève à qui il peut parler, sur qui il peut agir et qui peut agir sur lui. » (Brousseau, 1988, p. 24). Selon ce schéma, l’enseignant agissant sur la situation est en interaction, d’une part, avec l’élève et, d’autre part, avec la situation d’apprentissage. Suivant les développements plus récents sur la structuration du milieu, en particulier les travaux de Bloch (1999), le milieu ou le système antagoniste de l’enseignant est défini comme le système élève-milieu de l’élève. L’enseignant peut donc agir directement auprès de l’élève ; il le fera principalement sur le registre de l’oral, mais aussi sur le milieu avec lequel l’élève interagit, sur les règles du jeu. Il pourra alors agir sur d’autres registres que nous verrons, subordonnés, dans les extraits étudiés, à celui de l’oral.

Il est ici utile de référer au concept d’interactions tel que défini par Conne (2002). Partant du fait que l’activité cognitive est interaction entre un sujet et un ou des objets, Conne distingue deux niveaux d’interactions selon que le milieu, désignant l’ensemble des objets interreliés dans et par les interactions cognitives, contient ou non des sujets. Les interactions cognitives avec un milieu comportant des sujets dotés eux-mêmes de connaissances sont spécifiées en tant qu’interactions de connaissances. Ainsi, nous entendons par interactions didactiques des interactions cognitives relevant des deux niveaux au sein d’un système didactique.

Les négociations de contrat, évoquées par Brousseau (1988), sont pour l’enseignant une manière de rechercher une prise de contrôle sur la situation didactique, et c’est dans l’interaction avec les élèves et leur milieu que cette recherche se fonde. Nous souhaitons approfondir notre connaissance des stratégies mises en oeuvre dans la recherche d’une prise de contrôle à travers les échanges verbaux, en tant qu’interactions de connaissances, au cours d’une leçon de mathématiques.

Les situations ordinaires d’enseignement, et surtout celles des classes de l’enseignement spécialisé, cherchent à éviter la production d’erreurs. Puisque sont rarement réunies les conditions nécessaires pour assurer une rétroaction suffisamment puissante permettant à l’élève de constater sa réussite ou son échec, c’est à l’enseignant que revient la responsabilité de réagir aux erreurs. L’attention de l’enseignant de ces classes est donc largement sollicitée pour suivre le travail de chacun des élèves et intervenir pour diriger, piloter la démarche de l’élève, ou encore pour modifier, adapter le milieu pour que l’élève engage la conduite attendue. L’enseignant cherche donc à exercer un certain contrôle sur la situation didactique dans le but d’amener les élèves à exercer à leur tour, donc, un contrôle sur la tâche mathématique en mettant en oeuvre les connaissances visées. Dans le cas où le milieu en tant qu’image du savoir fait défaut à la situation didactique, l’enseignant et l’élève se trouvent confrontés à négocier avec l’ignorance.

C’est dans cette perspective que nous interprétons l’épisode suivant qui a lieu dans la classe pour élèves en difficulté d’apprentissage. Les élèves doivent collectivement trouver la solution à un exercice tiré d’un manuel scolaire. Il leur faut trouver le « truc » par lequel 6 grosses bougies et 3 petites bougies sur un gâteau d’anniversaire représentent 63 ans. Un élève propose une première solution : chaque bougie représente 7 ans (9 bougies × 7 ans/bougie = 63 ans). L’enseignante est évidemment surprise de cette réponse, n’ayant pas prévu une telle possibilité. La solution n’étant pas celle attendue, l’enseignante, sans la rejeter directement, invitera les autres élèves à faire d’autres propositions. Un autre élève proposera effectivement que chaque grosse bougie vaut dix ans et chaque petite, un an. L’enseignante retiendra cette solution de manière à ce que les élèves puissent utiliser ces valeurs pour trouver l’âge correspondant à différents gâteaux d’anniversaire. Au terme de l’activité, l’enseignante se trouve toutefois fort gênée que la solution du premier élève soit restée en suspens. Elle ira à la rencontre de l’élève pour lui préciser que sa réponse, bien qu’excellente, n’était pas celle attendue.

La réponse de l’élève dévoile la pauvreté du milieu à réagir (par exemple, en offrant des contre-exemples et en rétrécissant ainsi le choix des possibles). Le défaut de cet exercice sur la numération de position est que l’on ne sait rien de la base. La sélection de cet exercice, par l’enseignante, repose sur le fait que la situation présente de manière « transparente » les valeurs associées à chacun des chiffres selon leur position dans le nombre. Le manuel scolaire agit à titre d’expert pour elle, ce qui la dispense d’interroger a priori la situation. Cependant, le nombre 63 est mal choisi puisque la somme de ses chiffres est un diviseur du nombre. Ce qui se présente alors comme un imprévu pour l’enseignante ne risquait pas de se produire avec d’autres nombres (par exemple : 27, 53) ; ceux-ci auraient pu, par ailleurs, être utiles pour invalider la réponse « une bougie pour 7 ans ». Les interactions avec le milieu que le manuel a donc prévu, et que l’enseignante endosse à son insu, sont donc fictives, car la situation est non spécifique au savoir visé. Selon Fregona (1995), dans une interaction fictive, le milieu est constitué d’objets généraux, non spécifiés par rapport au savoir. L’autrice distingue les interactions fictives et effectives en précisant que, dans l’interaction effective, « le sujet reçoit de l’extérieur des sanctions non prévues de sa part : le contrôle de ses actions est assumé en partie par un système extérieur » (p. 62) [1].

La réponse de l’élève, juste mais non retenue, est un épisode où l’enseignante se révèle dans l’incapacité de modifier « à chaud » le milieu pour entrer en interaction avec un objet que l’élève pourra reconnaître comme celui avec lequel il interagit lui-même. L’enseignante n’arrive pas à jouer avec l’étonnement, pourrions-nous dire, non seulement à cause des solutions mathématiques possibles (dans N) qu’elle n’a pas anticipées et qui la laissent démunie, mais également par la gêne de prendre en compte un objet de savoir qui ne figure pas dans la finalité de sa leçon ; autrement dit, en s’inspirant de Conne (1999a), la connaissance induite par la situation n’est pas reconnaissable comme le savoir que l’enseignante se proposait d’enseigner.

La spécificité des interactions didactiques dans l’enseignement spécialisé

Favre (1997, 1999) considère l’échec comme une contrainte qui pèse sur l’institution de l’éducation spécialisée. Dans cette perspective, son étude vise à spécifier, au regard de l’enseignement ordinaire, les effets de la contrainte de l’échec sur l’enseignement dans une classe d’adaptation scolaire. Son étude l’a conduit à distinguer trois composantes de la contrainte de l’échec. La première est celle de « l’échec préalable » des élèves. Ses effets sont visibles dans le recours à des moyens spécifiques d’enseignement dont la mise en oeuvre conduit à la reconduction d’un processus d’enseignement. Une deuxième composante est celle de « l’échec effectif » des élèves à résoudre les tâches qui leur sont soumises. Les effets spécifiques de cette composante sur l’enseignement portent sur la durée de l’échec au sein des échanges. Cet échec occupe un espace didactique important, l’enseignant visant à éradiquer l’échec au moment même où il se produit. Nos expériences des classes d’adaptation scolaire rejoignent celles de Favre (1997, 1999). L’enseignant de l’adaptation scolaire traque les erreurs des élèves de façon à pouvoir mettre en oeuvre un dispositif qui vise non seulement à dévoiler l’échec, mais surtout à le déconstruire pour que l’échec soit « chassé » par le savoir. Une troisième composante identifiée par Favre, issue des deux premières, est « l’échec latent » des élèves à pouvoir résoudre ultérieurement les tâches qui leur seront soumises. Nous pouvons référer à cette composante pour situer les inquiétudes des enseignants de l’adaptation scolaire à proposer des tâches trop difficiles à leurs élèves. Cette troisième composante est associée chez Favre (1997) « à la constitution d’une théorie personnelle chez l’enseignant qui sous-tend une conception du rôle de l’enseignant comme « garant du sens et guide de la compréhension […] des élèves » (p. 173).

La ventilation en différentes composantes de la contrainte de l’échec permet de mieux saisir comment des conditions particulières de l’adaptation scolaire produisent une spécificité des échanges au sein du système didactique. L’analyse de Favre se situe du côté des effets, sur l’enseignement, des appréhensions, du repérage et du traitement d’échecs ou de difficultés des élèves. Rappelons-nous que, chez Brousseau (1988), l’échec de l’enseignement-apprentissage est relatif aux glissements de sens que l’enseignant n’a pu contrôler.

Nous interrogeons cependant le fait de considérer l’échec comme une contrainte qui pèse sur l’enseignement spécialisé. La mise en oeuvre des conditions différentes de celles de l’enseignement ordinaire vise à aménager un milieu adapté aux élèves qui ont rencontré l’échec en milieu régulier. Que cet échec soit du côté de l’institution ou des élèves ne change rien au fait que ce sont des élèves qui sont identifiés comme étant en difficulté, ayant des besoins particuliers. Dans cette perspective, l’échec préalable est bien évidemment une spécificité, une caractéristique de ces classes. Mais si l’échec préalable est une de leurs spécificités, est-ce pour autant une contrainte inhérente à leur institution ? L’échec auquel nous référons relève d’une autre institution, celle de l’école ordinaire. Autrement dit, est-ce que l’échec de l’école ordinaire survit dans l’école spécialisée ?

L’échec en classe ordinaire est celui de la réussite au regard des programmes d’études. Il n’existe pas d’échec semblable dans les classes spécialisées, puisque le programme ne pèse pas de la même manière. En raison de l’hétérogénéité des groupes-classes de l’adaptation scolaire, l’évaluation ne peut être effectuée selon des critères comparables à celles de la classe ordinaire. En revanche, l’enseignement en adaptation scolaire comprend une fonction d’évaluation presque en continu par le suivi très étroit du travail des élèves. Cette fonction est d’ailleurs une clause implicite des classes dont la taille des groupes d’élèves est réduite. L’enseignant cherche à éviter que les élèves errent trop longtemps et se charge donc d’intervenir promptement auprès de l’élève plutôt que sur son milieu. Un investissement des erreurs qui retient le temps peut conduire à un morcellement ou à une modification des savoirs visés (Favre et Cange, 2003). Il faut préciser, pour mieux saisir comment la capture et le traitement de l’erreur répondent à des nécessités pédagogiques pour l’enseignant, que l’erreur est considérée comme constitutive de la connaissance [2]. Elle est à ce titre un objet tout désigné pour élaborer une intervention qui se veut à la fois économique, c’est-à-dire bien ciblée dans le feu de l’action et personnalisée. Cependant, elle peut participer d’une dynamique d’interactions pouvant potentiellement affaiblir la dévolution (l’engagement de l’élève) et renforcer la pérennisation du contrat didactique.

Il y a une tension réelle dans l’éducation spécialisée entre, d’une part, la recherche d’une démarcation avec l’enseignement ordinaire et, d’autre part, la ligne d’horizon, de normalité que présente l’école ordinaire par la pression qu’exercent les politiques d’intégration scolaire. Aux enseignants des classes de l’adaptation scolaire est donc dévolue la responsabilité de mettre en oeuvre des stratégies d’enseignement adaptées à chacun des élèves (d’où les effectifs réduits). Toutefois, cet enseignement est balisé par les repères institutionnels offerts par l’école ordinaire pour que soient « exportables » les acquisitions des élèves en dehors de l’école spécialisée, autrement dit, pour que les apprentissages effectués puissent être reconnus par l’école ordinaire. La recherche de moyens et de stratégies pédagogiques et didactiques n’est donc pas totalement libre des pratiques d’enseignement des classes ordinaires. Cette tension devrait alors être visible à travers les échanges didactiques, soit directement par une intervention sur l’élève, soit par une intervention sur le milieu de l’élève.

La spécificité à travers les interactions langagières dans l’enseignement spécialisé

Comment, dans le cours normal des interactions d’une leçon de mathématiques, la question de l’adaptation de l’enseignement se pose-t-elle ? Suivant les travaux de Favre (1997), nous retenons comme hypothèse que ce n’est pas tant les moyens mis en oeuvre que la durée des échanges qui rendent spécifiques les interactions didactiques dans les classes pour élèves en difficulté, et, dans cette durée, le contenu qui alimente et fait l’enjeu des échanges.

L’enseignant de la classe spéciale cherche dans le hic et nunc les occasions d’apprêter son enseignement aux difficultés, aux erreurs de l’élève au moment où elles se présentent. C’est ainsi que les échanges verbaux, relativement serrés sous la forme question et réponse, sont intenses dans ces classes (Giroux et René de Cotret, 2001). Le repérage et le traitement des erreurs sont une forme d’évaluation continue au sein même de l’enseignement spécialisé visant à l’adaptation de l’enseignement, ce qui n’est pas sans effet sur les connaissances mobilisées dans ces échanges. Ils se prêtent particulièrement aux échanges lors des moments de correction. Nous procédons à l’analyse des interactions langagières au cours de la correction d’un travail portant sur l’exercice suivant : « Écris le nombre qui est 1 de plus que 13 ». L’extrait suivant illustre l’échange observé dans une classe d’élèves en difficulté d’apprentissage au premier cycle du primaire (7 à 10 ans).

La difficulté de l’élève relève de l’interprétation de l’expression « 1 de plus que… » et non pas de l’évocation de l’écriture du nombre 13 comme semble pourtant l’anticiper l’enseignante. La question à laquelle semble avoir répondu l’élève est celle-ci : « Si je dis 1 (un) chiffre de plus à l’écriture 1, 3, quelle écriture est-ce que j’obtiens ? » L’écriture comprendra alors non pas deux mais trois chiffres, le troisième étant une répétition d’un chiffre précédent : 1, 3, 3. Autrement dit, l’élève travaille sur des écritures de nombre, demeurant d’ailleurs dans le même registre que la question posée par l’enseignante, et non sur des nombres. L’enseignante cherche à travers l’échange la manière dont l’élève a produit cette réponse. Son insistance convainc évidemment l’élève de l’inadéquation de sa réponse mais pas de son modèle de résolution. Il proposera alors « 101 ». L’écriture de ce nombre comporte la même caractéristique que celle de 1 3 3, soit la répétition d’un chiffre, le 1.

L’analyste, en transcrivant à l’écrit le code numéral treize (13) et les chiffres (1, 3, 3, à l’oral), peut déjà voir une liaison et refaire alors en différé, comme un seul travail, celui de l’élève et de l’enseignante. L’enseignante, pour sa part, est prise dans l’action et boucle en mettant en évidence que la recherche du successeur (ce qui vient après 13) et la recherche de « 1 de plus que… » (13) sont deux manières de produire un même nombre. Notons qu’établir cette relation exige un travail important et nécessairement long de coordination des connaissances sur la suite des nombres et les opérations pour tous les élèves (Giroux et Ste-Marie, 2001 ; Giroux et Lemoyne, 1998).

Dans les leçons suivantes, il y aura beaucoup d’exercices de rappel sur « 1 de plus » et « 1 de moins ». Plus ces rappels seront nombreux, plus grande sera la confusion chez les élèves. Leur travail va reposer essentiellement sur les liaisons entre « de plus » et « après », mais également entre « de moins » et « avant » selon un contrat classique de répétition, d’entraînement. Précisons qu’en contexte de résolution de problèmes, cette liaison n’est pas garante de réussite (par exemple : Jean a 5 billes. Il a 1 bille de plus que Marie. Combien de billes a Marie ?).

Fonctions didactiques attribuées au traitement public des erreurs sous le registre de l’oral

À quelles nécessités semblent répondre les demandes d’explication adressées publiquement à l’élève qui produit une erreur ? Que poursuit l’enseignant lorsqu’il demande aux élèves de verbaliser sur leur erreur ? Nous explorons des éléments de réponse en nous appuyant sur le protocole que nous venons de présenter.

L’intervention de l’enseignante suppose qu’elle identifie l’erreur comme un produit de l’interaction de l’élève avec la tâche, ce qui rend recevable l’erreur et lui confère une certaine légitimité. Il y a donc, par cette intervention, une reconnaissance de l’activité mathématique de l’élève. Cette reconnaissance agit comme garde-fou de l’échange, bien que la réponse soit inintelligible aux yeux de l’enseignante. Cette reconnaissance permet de maintenir et de baliser l’échange par la tâche, le contenu et permet également d’éviter le procès de l’élève. Le traitement de l’erreur est alors utile pour adapter l’enseignement à l’interaction de connaissances nécessaires à l’échange didactique.

C’est sur la légitimité que nous venons de décrire que se fonde la transformation de l’erreur en objet d’enseignement ; l’enseignante lui attribue alors une fonction d’aide à l’apprentissage, à la conceptualisation. Par l’injonction donnée à l’élève de développer les raisons de sa réponse, l’enseignant espère que la connaissance qui a produit l’erreur ne puisse résister à sa formulation. L’intention de l’enseignant est que le passage au registre de l’oral va permettre à l’élève de prendre conscience de son erreur et de la rejeter. Cependant, le passage de l’action à la formulation ne relève pas d’un simple jeu de calque. C’est en ce sens, d’ailleurs, que nous interprétons les passages suivants de Vergnaud (1998) : « La mise en mots des connaissances-en-acte est difficile » (p. 289). Et plus loin :

Dans l’action, nous ne prélevons qu’une petite partie de l’information présente et nous en utilisons une partie plus petite encore. Dans la communication, nous sommes encore plus sélectifs, et laissons à autrui la charge de reconstituer, à partir de bribes d’énoncés et de rares énoncés complets, qui sont le lot habituel de la communication orale dans le travail, le sens des messages que nous lui envoyons.

p. 289-290

Le protocole l’illustre. L’élève n’explique pas à l’enseignante sa réponse mais s’engage plutôt dans la recherche d’une nouvelle réponse qui vient se substituer à la première. Elle est d’ailleurs formulée comme une offre, ce qui traduit bien la dynamique interactive malgré la confusion dans laquelle semblent plonger l’enseignant et l’élève. Une demande de précision répétée par un enseignant devient, du point de vue de l’élève, un moteur de recherche pour trouver une nouvelle solution. En ce sens, l’élève cherche à corriger l’erreur et l’enseignant à y remédier. La correction de l’erreur renvoie à la simple substitution de réponses alors que la remédiation vise davantage un apprentissage par adaptation, fondé sur le rejet d’une connaissance non appropriée. Dans le cas que nous venons d’étudier, l’enseignant n’a pas les moyens didactiques pour susciter cet apprentissage du fait de la pauvreté du milieu ; la situation n’est pas pertinente au regard de la connaissance visée.

Ainsi, l’erreur offre une occasion d’adapter l’enseignement non pas aux besoins particuliers de l’élève mais à son activité cognitive. L’enseignant espère qu’en étant invité à justifier, à expliquer la réponse erronée, l’élève confrontera le rapport qu’il entretient avec la connaissance, source de l’erreur relevée. L’erreur est retournée à l’élève qui la produit en tant que question mathématique qui lui est propre.

Selon Mercier (1996, 1998), dans l’urgence de l’action, l’ignorance porte rarement sur un objet correctement identifiable par l’enseignant. Sous peine que la situation mette alors en péril autant l’apprentissage que l’enseignement, l’enseignant doit agir, mais il ne peut le faire sans engager lui-même des connaissances et des savoirs (Bloch, 1999 ; Conne, 1999b). Dans l’extrait que nous venons d’étudier, la connaissance engagée derrière l’erreur n’est pas identifiée par l’enseignant. Il nous semble, dès lors, que l’ignorance rencontrée dans les interactions didactiques n’est pas tant celle de l’élève qui serait gérée par l’enseignant mais plutôt un élément dynamique de la situation d’enseignement-apprentissage qui implique donc à la fois l’enseignant et l’élève.

L’analyse que nous venons d’effectuer a été centrée sur le traitement ponctuel et public d’une erreur produite par un seul élève lors d’une activité de correction. Qu’en est-il toutefois lorsque l’erreur est révélée par plusieurs élèves lors d’une situation d’enseignement ?

Un instrument dans la recherche d’une prise de contrôle par l’enseignant : la verbalisation

Nous examinons un autre cas de figure dans la recherche d’une prise de contrôle sur la situation repérée dans les interactions didactiques dans une classe d’adaptation scolaire. Le cas étudié est la progression d’une leçon d’enseignement sur la composition additive dans une classe d’élèves dysphasiques de 6 et 7 ans. La suite d’exercices soumise aux élèves comporte un changement de registres sémiotiques qui modifie le milieu et affecte substantiellement l’activité de résolution. Ce changement de milieu échappe d’abord à l’enseignante qui se trouve confrontée à son incompréhension des erreurs produites par ses élèves. Toutefois, par un jeu d’interactions de connaissances avec plusieurs élèves, l’enseignante modifie sa représentation de la tâche proposée et, du coup, ses interactions avec les élèves. Ses interventions ne sont plus centrées sur l’élève mais sur son milieu, ce qui modifie la tâche qu’il a à effectuer. Le contrôle qu’elle tente d’exercer sur la situation engage sa propre activité mathématique qu’elle considère « analogue » à celle que l’élève doit engager. Nous faisons l’hypothèse que les changements de contrat peuvent découler d’une modification de la représentation que se fait un enseignant de la tâche mathématique et que cette modification est générée par ses interactions de connaissances avec les élèves.

Analyse a priori de la fiche

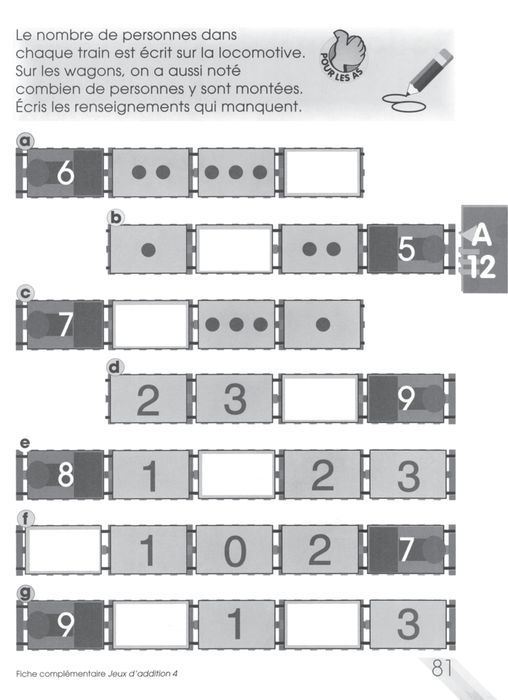
Au cours de cette leçon, les élèves doivent compléter une page de manuel scolaire portant sur la composition additive. Pour chacun des sept exercices, une locomotive et un certain nombre de wagons sont illustrés. Sur la locomotive est indiqué le nombre total de personnes montées dans le train. Sur certains wagons est inscrit, soit par des points, soit par l’écriture usuelle, le nombre de personnes qui sont montées. Considérant, d’une part, le nombre total de passagers inscrit sur la locomotive et, d’autre part, le nombre de passagers représenté sur certains wagons, l’élève doit, selon le libellé de la consigne, « écrire les renseignements qui manquent », c’est-à-dire représenter sur les wagons vides, soit par un dessin de points, soit par une écriture, un certain nombre de passagers.

La fiche porte donc sur la recherche d’une partie ou de plusieurs parties, étant donné un tout et un certain nombre de parties. Les problèmes soumis se présentent en contexte cardinal, mais les stratégies de résolution peuvent faire appel au dénombrement et à la réunion de collections (contexte cardinal) ou encore au comptage et à l’ajout (contexte ordinal). Nous décrivons brièvement les stratégies au regard des variables de chacun des exercices. Cette analyse permettra de mieux saisir les différents enjeux mathématiques au coeur des interactions tout au long de la leçon.

Figure 1

Fiche sur la composition additive tirée de Lyons et Lyons (1998)

Fiche sur la composition additive tirée de Lyons et Lyons (1998)

-> Voir la liste des figures

Dans les trois premiers exercices (a, b, c), la tâche consiste principalement à compléter une collection par réunion et par dénombrement d’objets. Chaque train est composé d’une locomotive sur laquelle est inscrite en chiffres une somme, et de trois wagons « de points », dont un est vide. L’élève doit y dessiner le nombre de points manquants pour obtenir la somme inscrite sur la locomotive. Pour ces trois exercices, la stratégie de base, celle qui est suffisante à la réussite, est le dénombrement. Elle peut comporter différentes variantes, mais elle consiste essentiellement à dénombrer le nombre de points dessinés et à procéder à des dénombrements successifs à la suite de l’ajout d’un point, et ce, jusqu’à ce que le cardinal de la collection des points dessinés corresponde au nombre recherché (le total des passagers).

Une autre stratégie plus évoluée, que nous appelons comptage [3], consiste, à partir du nombre de points dessinés, à avancer dans la suite des nombres jusqu’à l’atteinte du nombre cible, le tout (le total des passagers). Le nombre de points à dessiner correspond au nombre de déplacements à effectuer dans la suite des nombres pour atteindre le nombre cible. Prenons l’exemple de l’exercice (b) où trois points sont dessinés dans deux wagons et où le nombre cible à atteindre est 5 : a) je dénombre les points déjà dessinés (3) ; b) je pars de 3 et avance de deux positions dans la suite des nombres pour atteindre 5 ; c) 2 est le nombre de points que je dois dessiner dans le wagon vide. Ainsi, le déplacement est contrôlé par deux réseaux en activation : un premier pour avancer dans la suite (à 4, à 5) et un second pour dénombrer les déplacements [à 4 (1), à 5 (2)] correspondant au nombre qui convient pour compléter la composition additive (3 et 2 font 5). Une difficulté fréquente dans l’application de cette stratégie est de contrôler les bornes, les nombres de départ et d’arrivée. Il faut mémoriser le nombre de départ et avancer depuis ce nombre sans l’intégrer dans le comptage [exemple de cette erreur : 3 et 3 font 5 : à 3 (1), à 4 (2), à 5 (3)]. Il faut aussi mémoriser le nombre cible pour bien contrôler le nombre auquel on doit s’arrêter et ne pas confondre les deux réseaux [exemple de cette erreur : 2 et quoi font 4, réponse : 4 à 3 (1), à 4 (2)].

La stratégie de comptage fait appel à des connaissances plus évoluées que le dénombrement. En effet, le contexte cardinal suggère des stratégies de dénombrement par réunion des collections de points dessinés. On peut dès lors facilement se réajuster sur les points à dessiner en procédant par dénombrements et ajustements successifs. Cependant, les stratégies de comptage réfèrent à un contexte ordinal et correspondent non pas à une réunion de collections mais à un ajout sur une collection initiale. Pour contrôler cet ajout, il faut activer et contrôler deux suites dont l’une sert à dénombrer les déplacements depuis un nombre de départ jusqu’à un nombre cible.

Dans les trois exercices suivants (d, e, f), ce sont des nombres, et non plus des points, qui sont inscrits sur les wagons. L’élève doit inscrire un nombre dans le wagon vide. La tâche n’est plus du tout la même. Il ne s’agit plus de compléter une collection mais une composition additive de manière analogue à une addition lacunaire (« Si on a 2 et 3, quel nombre manque-t-il pour obtenir 9 ? »). Les stratégies de dénombrement sont peu efficaces pour réussir ces exercices. Il serait en effet possible, mais très coûteux, de dessiner une collection de points pour chaque wagon et ainsi modifier le problème pour le rendre semblable aux exercices précédents.

Pour effectuer ces exercices, l’élève doit d’abord trouver la somme des nombres inscrits dans les wagons ; il peut le faire, soit par dénombrement et réunion des deux collections (en recourant aux doigts par exemple : sortir 3 et 2 doigts et dénombrer pour obtenir 5), soit par comptage [3 à 4 (1) à 5 (2)]. Spécifions que certaines sommes peuvent être rappelées directement par les élèves (« Je sais que 3 et 2 font 5. »). Partant de cette somme, il doit identifier le nombre qui permet d’atteindre le nombre cible (« 5 et quel nombre font 9 ? ») correspondant à la partie du tout recherchée. Nous avons décrit au paragraphe précédent comment une stratégie de comptage permet de trouver ce nombre [4]. Les stratégies de comptage sont, pour ces exercices, les plus efficaces et les plus économiques.

Enfin, au dernier exercice (g), deux wagons sont vides ; l’élève a donc à trouver deux nombres pour compléter la composition additive. L’élève doit identifier une partie du tout (total des passagers) pour ensuite considérer cette partie comme un tout à décomposer en deux parties. Des stratégies bien sûr diverses peuvent être employées et certaines permettent de contourner la complexité du problème en procédant, par exemple, par essais et ajustements successifs. Ce sont toutefois les stratégies de comptage qui demeurent les plus efficaces.

Analyse des interactions au cours de la leçon

L’enseignante présente la tâche et complète, avec la participation des élèves, le premier exercice. La représentation de l’enseignante à propos de l’activité que les élèves ont à accomplir fait appel à l’objet « comptage ». La stratégie qu’elle suggère, comme en témoigne l’extrait qui suit, consiste à dénombrer le nombre de points dessinés, et à anticiper le nombre de points à ajouter par comptage pour obtenir le nombre total de passagers. Une fois ce nombre identifié, l’élève est invité à dessiner le nombre de points [par exemple : 3, à 4 (1), 5 (2) ; je dois dessiner 2 points pour obtenir 5]. Des stratégies élémentaires de dénombrement sont toutefois suffisantes pour effectuer les trois premiers exercices (a, b, c). L’élève peut dénombrer les points déjà dessinés et poursuivre son dénombrement par l’ajout successif d’un point jusqu’à l’atteinte du nombre visé. L’élève peut également « re-dénombrer » la collection totale après chaque ajout (repartant ainsi toujours de 1). Ce sont ces stratégies de dénombrement que les élèves mettent en oeuvre et c’est donc avec l’objet « dénombrement » que les élèves interagissent. Tant que l’enseignante atteste la réussite des élèves, le décalage entre sa représentation de l’activité des élèves et leur activité effective n’est pas visible au sein des interactions. La représentation de l’enseignante est élaborée sur la base des savoirs mathématiques qu’elle-même mobilise pour effectuer la tâche ; ses interventions sont donc dirigées par son propre travail mathématique.

Présentation de la consigne

Pour les trois premiers exercices (a, b, c), il y a peu d’échanges entre les élèves et l’enseignante. Si l’enseignante circule et invite quelques élèves à poursuivre leur travail, il n’y a pas d’interventions de sa part qui dirige le travail mathématique des élèves. À partir du quatrième exercice (d) les élèves ne doivent plus dessiner un nombre de points, mais écrire le nombre qui convient. L’enseignante intervient alors pour spécifier le registre, l’écriture du nombre, dans lequel la réponse est attendue. La résolution de la tâche par l’enseignante est sans doute sous le contrôle du rappel des faits additifs. La transposition qu’elle opère pour l’enseignement est, lui, sous le contrôle du comptage, et ce, peu importe le registre dans lequel la tâche est proposée. Pour l’enseignante, le passage à l’écriture du nombre n’est donc pas considéré comme une variable pouvant affecter les stratégies de l’élève. Derrière, on peut supposer que se profile cette conception de l’apprentissage selon laquelle un objet de savoir traversant successivement différents registres de représentations selon la chaîne « concret à figuratif à abstrait » (l’écriture symbolique étant considérée comme abstraite) assure une avancée « en douce » dans le savoir mathématique.

Passage à l’écriture du nombre

Comme le montre l’extrait qui précède, des tensions émergent entre l’enseignante et les élèves. Les interventions auprès de Stéphane ou encore celles qui visent à relancer le travail d’autres élèves traduisent l’impatience de l’enseignante qui juge que les élèves manquent à l’effort. L’action professorale est donc dirigée vers les élèves. L’échec presque généralisé des élèves au cinquième exercice (e) conduit l’enseignante à piloter étroitement leur travail produisant ainsi des effets de contrat de type « Topaze » [5]. Mais cet échec des élèves stimulera une investigation de l’enseignante auprès des élèves. Pourquoi l’exercice (d), qui exige l’écriture, est-il réussi alors que l’exercice suivant (e) est échoué ? Elle parvient alors à lever son ignorance en cherchant les raisons de l’ignorance des élèves du côté du savoir : comment l’élève a-t-il su répondre à l’exercice (d) ?

Investigation sur la stratégie en (d)

Elle est informée par l’élève que l’exercice (d) est réussi par défaut. À l’exercice (d), sur les deux premiers wagons sont inscrits respectivement les nombres 2 et 3. Le nombre total des passagers inscrit sur la locomotive est 9. Les élèves ont inscrit 4 sur le troisième wagon non pas en considérant le nombre total, mais plutôt en complétant une suite numérique : 2, 3, 4. La tâche à partir de (d) est, effectivement, profondément modifiée. Il ne s’agit plus de compléter une collection d’objets mais de travailler sur une composition additive selon le modèle de l’égalité lacunaire : 2 + 3 + ___ = 9. Les stratégies de dénombrement conviennent peu à ce type de relation parce que complexes à mettre en oeuvre (par exemple : lever 9 doigts, retirer 2 et 3 doigts, dénombrer les doigts restants). Elles sont, somme toute, peu utiles alors que les stratégies de comptage, elles, deviennent des stratégies optimales [5 à 6 (1), à 7 (2), à 8 (3), à 9 (4)]. Le comptage, comme nous pouvons l’observer dans cet exemple, exige l’activation de deux réseaux et donc un niveau de contrôle de la part de l’élève plus important que celui exigé pour le dénombrement. La représentation que se fait l’enseignante du travail mathématique des élèves sera, à partir de cet épisode, transformée. Ses interventions viseront alors, soit à piloter la démarche de l’élève, soit à modifier le milieu de l’élève de manière à faciliter le recours au dénombrement.

L’enseignante court-circuite ainsi les procédures de comptage sur lesquelles elle tablait dans la première partie de la leçon. Elle tente de rendre transparente la réponse que l’on peut obtenir en l’accompagnant d’une activité de dénombrement. Ainsi, corrigeant les élèves au fur et à mesure, elle procède par comptage à voix haute en levant soit les doigts ou encore en marquant sur la fiche de l’élève les points correspondant aux nombres écrits. Par ces interventions, l’enseignante agit alors sur le milieu en jouant sur les variables de manière à réduire la complexité de la tâche et donc à adapter le milieu de l’élève aux stratégies de dénombrement.

Modification du milieu de l’élève par l’enseignant

Dans l’extrait qui précède, l’enseignante assume d’abord l’addition des nombres fournis et, dans un second temps, elle prend en charge un premier réseau (1, 2, 3, 4, 5, … 6, … 7, … 8), sur lequel l’élève peut jumeler le deuxième réseau [7 (1), 8 (2)]. L’élève peut ainsi dénombrer les deux dernières quantités et identifier le nombre manquant. L’enseignante considère son procédé suffisamment transparent pour que l’élève puisse s’y modeler (« Je viens de te le montrer. »). Pour trois des élèves considérés plus faibles, elle dessinera dans les wagons les points correspondant au nombre inscrit, simplifiant le problème pour le rendre semblable aux exercices a, b et c. Les élèves corrigent toutefois par dénombrements et ajustements successifs. Il faut noter qu’au cours de sa correction, l’enseignant valide ou invalide elle-même la réponse produite par l’élève.

Recherche d’une synchronisation des activités mathématiques

Ce qui frappe, à la lecture du protocole, c’est la place qu’occupe la « parole » de l’enseignante comparativement à celle des élèves. Dans cette leçon où les élèves, en nombre réduit (7), ont à remplir individuellement une fiche, l’enseignante, elle, semble en situation d’enseignement collectif. Bien que chacune de ses interventions s’adresse à un élève en particulier, plusieurs sont faites avec la tonalité utilisée pour viser tout le groupe d’élèves. Ces jeunes élèves ayant des problèmes de langage importants répondent peu aux questions de l’enseignante, lui laissant le soin d’interpréter les réponses qu’ils produisent. Mais il nous semble qu’au-delà des difficultés d’expression verbale de ces élèves, nous pouvons y déceler la difficulté, pour l’enseignante et les élèves, à synchroniser leurs pensées. À ce propos, il nous semble utile de citer Conne (1999a) pour mieux saisir comment la fonction de l’échange, et sous plusieurs registres, vise à favoriser cette synchronisation.

[I]l est important de noter que les interactions des différents acteurs avec le milieu de la situation ne sont pas identiques ni substituables les unes aux autres. Pourtant, tous les échanges sont fortement marqués par les interactions que chacun entretient avec le milieu, et l’une des premières fonctions que ces échanges assurent est d’obtenir une certaine synchronisation des pensées. Cela est rendu nécessaire pour que la vitesse et les niveaux d’interactions varient d’un sujet à l’autre. En cela, le maître et l’élève se distinguent nettement, et on doit partir de l’idée qu’ils ne traitent pas exactement des mêmes mathématiques. Les jeux que laissent ces différences d’objets sont régulés par l’intermédiaire d’interprétations subjectives des traces et indices laissés par les sujets dans leur interaction avec le milieu : traces écrites, expressions verbales, etc. Les acteurs s’accordent ou ne s’accordent pas sur la production de ces traces et indices dans la mesure où ils sont compatibles avec leurs pensées respectives.

p. 33-34

Cette citation nous offre des outils pour comprendre comment la leçon progresse. Nous en dégageons succinctement les principaux éléments. L’analyse préalable de la fiche, réalisée par l’enseignante, lui suggère que c’est un exercice facile pour les élèves puisqu’il succède à une fiche où les élèves avaient à partager un certain nombre de fleurs dans des pots différents (par exemple, partager 8 fleurs dans 3 pots). Tout comme pour les trois premiers exercices de la fiche étudiée, la stratégie de dénombrement est suffisante pour partager les fleurs. Étant donné la parenté qu’elle repère entre les factures des fiches « fleurs » et « trains », sa proposition suppose que l’objet « comptage » est un savoir déjà là pour les élèves, une connaissance dont l’utilité aurait déjà été reconnue par les élèves. Elle amorce donc la leçon en suggérant une stratégie efficace pour l’ensemble des exercices de la fiche, stratégie qui fait appel à l’objet de comptage. Cette stratégie de « base » pour l’enseignante n’est pas celle engagée par les élèves. Leurs réussites aux quatre premiers exercices ne créent toutefois aucune rupture et rendent opaque la distance entre la représentation que l’enseignante se fait de l’activité mathématique des élèves et leurs activités effectives. Les élèves contrôlent la situation et il n’y a aucune raison d’interroger ce qu’ils font pour réussir. La situation progresse toutefois de manière inattendue pour l’enseignante. Si ses interventions font d’abord le procès des élèves (leur manque d’attention), elle se trouve rapidement elle-même démunie puisque l’objet comptage, voire le savoir qu’elle mobilise, ne lui permet pas de lever sa propre ignorance face aux erreurs des élèves.

La tâche change en fait quatre fois pour les élèves : 1) a, b, c ; 2) d ; 3) e et f ; 4) g. Par ses interactions avec les erreurs ou, plus précisément, grâce aux traces laissées par les élèves de leur interaction avec l’objet dénombrement, l’enseignante prend conscience qu’il y a un exercice que les élèves ne contrôlent pas, que la situation leur échappe dès qu’ils doivent traiter des écritures numériques plutôt qu’une représentation de ces nombres dessinée par des points de ces nombres. Elle n’arrive toutefois pas, dans l’urgence de l’action que son activité enseignante commande, à contrôler la situation d’apprentissage puisqu’elle n’arrive pas à « enrôler » efficacement « l’activité de l’élève dans une pratique mathématique » (Conne, 1999 a et b). Le contrôle est du côté de la situation. L’enseignante rencontre donc un problème d’enseignement. Ce problème relève d’une certaine manière de l’écart entre ce que cette tâche suscite, induit chez l’enseignante comme activité mathématique (résoudre une égalité lacunaire par une stratégie de comptage) et ce qu’elle induit chez les élèves (dénombrement pour compléter une collection). Il relève également du fait que l’enseignante semble reconnaître que les élèves n’ont pas à leur disposition les connaissances suffisantes pour effectuer la tâche selon le modèle de résolution qu’elle met elle-même en oeuvre et qu’elle tente de faire adopter par imitation aux élèves.

Par ses interventions successives auprès de certains élèves, l’enseignante entre en interaction avec un élément nouveau qui demeure relativement peu défini pour elle : la stratégie de dénombrement. La représentation qu’elle se fait de l’activité de l’élève est alors modifiée ; d’autres procédures de réussite nécessitent alors des interventions sur le milieu de l’élève. Autrement dit, l’enseignante joue sur les variables de la situation, à son insu, pourrions-nous dire. Jouer sur les variables conduit à morceler la tâche en prenant à sa charge le contrôle du comptage : l’élève peut alors dénombrer ce que l’enseignante lui présente (dénombrer les nombres récités lentement par l’enseignante ou les points que celle-ci dessine sur la copie de l’élève) et glisser sur le savoir qu’elle vise, soit la maîtrise du comptage. Elle rend, ce faisant, de plus en plus transparente sa propre activité, la manière dont elle « fait », « résout » le problème. L’enseignante cherche à travailler le milieu pour que celui-ci contienne des éléments dont les élèves peuvent se saisir pour compléter la fiche. Nous pouvons voir comment la prise en compte des connaissances de l’élève modifie le milieu de l’enseignante et sa représentation en tant qu’interface entre connaissances et situation (Brun et Conne, 1990). Le contrôle de plus en plus serré qu’elle opère réduit la marge d’incertitude autant du point de vue de l’enseignement que de celui de l’apprentissage. La recherche de la synchronisation des pensées conduit à une certaine dépendance de l’enseignante au regard de la pratique mathématique qu’elle cherche à imposer aux élèves.

Conclusion

Dans ce texte, nous avons examiné les connaissances en interaction, par des actes langagiers, dans des classes d’adaptation scolaire et, spécifiquement, dans le contexte où des erreurs produites par un ou des élèves induisent des épisodes où se révèle et se négocie l’ignorance. Les analyses montrent que l’investigation prononcée sur le traitement des erreurs est un investissement du savoir qui procède d’interactions de connaissances. Nous pouvons dégager quelques points communs des leçons analysées.

L’importance des interactions langagières semble induire la domination de la langue naturelle sur les autres registres sémiotiques dans l’échange. Certains extraits tendent à montrer que la langue naturelle, en « capturant » ou en subsumant les autres registres, peut être un obstacle à leur articulation. Les échanges entre l’enseignante et les élèves sont extrêmement serrés et, de là, parfois s’enfoncent parfois jusqu’à l’évanouissement du sens de l’enjeu mathématique. Les demandes soutenues adressées aux élèves pour expliquer leurs réponses ou encore le pilotage de leur démarche en témoignent. Il en résulte bien sûr des effets Topaze entraînant dans leur sillon des effets Jourdain [6], lesquels se présentent comme une « solution » au problème d’enseignement. Nos analyses éclairent ce problème en tant que corrélat à l’ignorance rencontrée par l’enseignant en situation effective. Le jeu particulier des échanges dans ces classes fait appel aux connaissances et aux savoirs des protagonistes. C’est donc un jeu qui investit le savoir, lequel, en retour, induit ou fait rencontrer l’ignorance de l’élève et/ou de l’enseignant.

Dans la suite de nos analyses, il nous semble opportun de revenir au schéma de Brousseau (1988) en proposant quelques considérations sur les trajectoires qui y sont illustrées. Rappelons que ce schéma distingue des trajectoires de la négociation du contrat didactique selon que l’échec est ou non reconnu par l’enseignant. La reconnaissance ou la non-reconnaissance de l’échec engage les connaissances et les savoirs de l’enseignant, mais également la frange d’ignorance qui les accompagne, dans ses interactions avec les élèves. Ainsi, ce qui est attribué en termes d’échec est orienté par l’activité mathématique de l’enseignant et sa représentation de l’activité de l’élève. L’attribution de l’échec se modifie sous l’effet des interactions qui visent à la synchronisation de ces activités. Ainsi, dans une même leçon, différentes trajectoires menant à différents effets de contrat (tels que Topaze, Jourdain ou Bloom [7]) peuvent être empruntées. Dans la leçon du « train », par exemple, l’échec des élèves aux derniers exercices révèle à l’enseignante de manière plutôt implicite, l’échec à utiliser les connaissances qu’elle jugeait nécessaires à la réussite des premiers exercices. L’attribution ou la non-attribution de l’échec et les phénomènes didactiques qui peuvent en découler s’inscrivent donc dans une dynamique d’interactions de connaissances.

Nous devons aussi souligner que les situations analysées ne comportent pas les éléments nécessaires pour assurer la rétroaction et sont peu pertinentes au regard du savoir visé [8]. Elles n’ont donc pas le potentiel pour comporter une dimension adidactique permettant d’ouvrir sur d’autres solutions en termes d’actions. Le champ des interventions des enseignants, faute de moyens didactiques, s’en trouve rétréci aux demandes de formulations qui exercent cependant une fonction didactique.

Des situations d’enseignement alternatives appuyées par des analyses a priori portant sur les notions en jeu dans des leçons traitées sont connues. Pour les dénombrements d’ordinaux, nous pouvons penser aux situations qui se basent sur des jeux de pistes qui permettent de travailler les relations entre un nombre de départ, un déplacement et un nombre cible. Le jeu « Rummy rami » permet également de travailler sur l’ordre de grandeur des nombres. Pour la numération, nous référons à la situation des carrelages (Coulomb, 1991) ou encore à celle des envahisseurs (Bloch, 2000), dans lesquelles des indications sur la base sont données.

Mais encore faut-il, pour que ces situations soient reconnues comme des solutions de rechange aux leçons étudiées, que les savoirs investis par chacune d’elles soient spécifiés. Pour la leçon sur le « train », le savoir visé par l’enseignante est l’addition et non le comptage (dénombrements d’ordinaux) qui n’est d’ailleurs pas identifié comme un objet d’enseignement. Au même titre que nous interrogeons l’approche par remédiation des difficultés chez les élèves, nous voulons éviter une approche par « remédiation » des situations d’enseignement qui ne viserait, du point de vue de l’enseignement, qu’à une substitution de situations. La formation continue ou la recherche collaborative par lesquelles on peut viser à faire dévolution aux enseignants de situations didactiques constituent en elles-mêmes des voies de recherche. De plus, les situations qui présentent le plus de potentiel comportent, au moment de leur réalisation, leur part de contingence avec lesquelles les enseignants et les élèves auront à négocier.

Nous avons inscrit ce texte dans la problématique plus générale de l’adaptation scolaire en nous interrogeant sur la spécificité des interactions langagières dans ces classes. Est-ce que les interactions décrites et analysées sont spécifiques à ces classes ? Ne relèvent-elles pas plutôt d’un phénomène didactique qui dépasse la spécificité de cette institution ? Nos analyses recoupent les analyses didactiques par lesquelles s’est constituée la notion d’ostension déguisée. Rappelons quelques passages de Salin (1999) pour apprécier le rapprochement :

Ratsimba-Rajohn (1977) définit la présentation ostensive comme la donnée par l’enseignant de « tous les éléments et relations constitutifs de la notion visée. » Puis, l’auteur complète ainsi la définition : « L’ostension consiste en l’utilisation, dans une situation d’enseignement, de la capacité supposée de l’élève de percevoir certains objets et en l’illusion que le fait qu’il les ait perçus est porteur d’une connaissance intellectuelle éventuellement générale et précise. » Ce n’est qu’au cours de la résolution des problèmes et exercices que l’enseignant, confronté aux difficultés et aux erreurs de ses élèves, est tenu d’interagir avec eux sous différents modes, par exemple par le moyen d’explications, en prenant en compte leurs conceptions, dans la mesure où ses propres connaissances, mathématiques et didactiques, le lui permettent.

p. 330

Cette citation convainc que cette notion est utile à l’interprétation des interactions que nous avons décrites. Il est fort probable que les exercices analysés induisent des interactions de connaissances de même nature en classe ordinaire. Nous ne disposons pas de données comparatives pour apporter des éléments précis de réponse. Cependant, en classe ordinaire, la réussite de plusieurs efface vite l’échec de certains et cela rend relativement rapide l’extinction publique des erreurs que certains élèves peuvent commettre (Favre, 1997). Des études comparant l’enseignement-apprentissage des mathématiques en classes ordinaire et spéciale sont nécessaires pour attaquer la question de la spécificité de l’adaptation scolaire. Ces études devraient permettre de préciser comment se contrastent l’échec et la réussite dans ces classes en précisant, à titre d’exemples, le caractère local ou non des réussites obtenues, les cas où la réussite ou l’échec fait dévier le savoir visé ou encore de préciser sous quelles conditions l’échec est traité publiquement par l’enseignant (et donc principalement sous le registre de la langue naturelle) ou encore renvoyé dans la sphère privée de l’élève, etc.

Les questions restent donc nombreuses. Nous espérons néanmoins que ce texte, à partir de l’analyse effectuée sur les échanges langagiers, contribue cependant à mieux cerner et caractériser les interactions de connaissances dans ces classes.